在没有随机对照的情况下如果做实验对比：双重差分法（结合虚拟变量回归）（五）

本篇文章Measuring Uplift Without Randomised Control — a Quick and Practical Guide提供了一种在没有随机对照实验的情况下测量干预效果的方法。文章的技术亮点在于介绍了Difference in Differences (DiD)方法，并结合线性回归和贝叶斯统计，提供了多种分析手段。

这里为什么DID要借用虚拟变量回归模型，再次举个例子方便理解：

假设你是一家咖啡店的老板，你在某个街区开了两家分店：A店和B店。这两家店的生意一直差不多，而且都在同一个城市，所以平时顾客流量变化趋势也差不多。
现在，你决定在A店附近竖起一块巨大的新广告牌，希望它能吸引更多顾客。B店附近没有新广告牌。你想知道这个广告牌到底有没有用，能让A店多卖多少咖啡。

这是一个典型的 DiD 场景，因为：

• 处理组 (A店)：受到了“新广告牌”这个处理。
• 对照组 (B店)：没有受到处理。
• 处理前/处理后：广告牌竖起来之前和之后。

这里构建的回归如下：
$销量=\beta 0+\beta 1\times 是否A店+\beta 2\times 是否放置广告牌+\beta 3\times (是否A店\times 是否放置广告牌)+其他因素+误差$

其中：

• 是否A店，虚拟变量，是A店，它就是1；如果是B店，它就是0，此时$\beta 1$的经济学含义：广告牌放置前的A店比B店多卖（或少卖）的销量。这反映了两家店在广告牌出现前的固有差异。
• 是否有广告牌，虚拟变量，$\beta 2$，如果没有广告牌，B店、A店在放置广告牌后 相对于放置广告牌前，销量会发生多少变化。这捕捉了整体的时间趋势（比如夏天咖啡卖得更好，或者城市消费水平整体提升了）
• 交互项，$是否A店\times 是否放置广告牌$，也是 DiD 的核心！当是A店且在广告牌后时期，这个项就是1，其他情况都是0；其中，$\beta 3$，就是我们最关心的“广告牌带来的额外销量”！它代表了广告牌对A店销量的净影响，已经排除了A店和B店的固有差异，以及整体的时间趋势。

---

---

1 双重差分法 (DiD)

这篇博客将探讨一些方法，包括双重差分法、OLS 与贝叶斯回归、以及方差分析和协方差分析。

一次电子邮件营销活动。一次更新的网站用户旅程。一种新药。在各个行业和专业领域，我们经常会问——我刚刚做的这件事，它的影响力有多大？

通常，回答这个问题的方法是设计一个实验，随机选择哪些人（或者更普遍地说，哪些单元）接受干预，哪些人不受干预。有些人不会收到电子邮件，或者看不到新的网站用户旅程，或者会收到安慰剂。然后，我们只需测量每个组的相关统计数据（销售额、转化率、存活率），并应用测试来确定差异是否显著（例如，比例的 z 检验或相关的 t 检验）。

但在这篇文章中，我感兴趣的是当你没有设置随机实验时该怎么做。

对于这个例子，我使用了 Kaggle 数据集，其中包含了欧洲最大连锁药店之一的销售数据。假设我想衡量附近一家竞争对手开业的影响——这就是我的干预或处理。“处理”在这个例子中有点反直觉，因为我预计它会对我的销售额产生负面影响。

为了简化问题，我们选择一组在 2013 年 4 月同时有竞争对手开业的门店作为处理组。我们的对照组将是一组没有任何竞争对手的门店。

import pandas as pd  
from pandas.tseries.offsets import DateOffset  
import seaborn as sns  
import matplotlib.pyplot as plt  
import matplotlib.ticker as tickerdf_sales = pd.read_csv("train.csv")  
df_stores = pd.read_csv("store.csv")  
df_sales["Date"] = pd.to_datetime(df_sales["Date"])df_stores_treat = df_stores[  (df_stores["CompetitionOpenSinceYear"] == 2013)&  (df_stores["CompetitionOpenSinceMonth"] == 4)&  (df_stores["CompetitionDistance"] < 1000)  ]df_stores_control = df_stores[df_stores["CompetitionOpenSinceYear"].isnull()].sample(int(len(df_stores_treat)), random_state = 40)   df_sales_treat = df_sales[df_sales["Store"].isin(df_stores_treat["Store"])]  
df_sales_control = df_sales[df_sales["Store"].isin(df_stores_control["Store"])]df_sales_treat["Group"] = 'Treat'  
df_sales_control["Group"] = 'Control'

我无法要求我的竞争对手随机选择在哪家门店附近开业，所以我不能仅仅比较有本地竞争对手的门店销售额与没有竞争对手的门店销售额——可能有很多其他因素在起作用。独立样本 t 检验不是一个选择。

我可以查看一家给定门店在竞争对手开业前后的销售额。但同样，可能有很多其他因素在起作用。如果销售额的变化不是因为竞争对手开业，而是因为季节性、管理层变动或负面公关呢？配对样本 t 检验也不是一个选择。

我需要同时利用我所拥有的所有信息——处理（竞争对手在附近开业）之前和之后的销售额，在受处理和未受处理的门店中。

这就是双重差分法 (DiD) 可能有用的地方。

• 第一个差分是处理组结果的变化——在我们的例子中，是那些在 2013 年 4 月有竞争对手开业的门店的销售额变化。这有时被称为处理组的平均处理效应 (ATT)。
• 第二个差分是对照组结果的变化——在我们的例子中，是那些在 2013 年 4 月没有竞争对手开业的门店的销售额变化。

在这两种情况下，“变化”都是根据用户定义的处理前和处理后时期来衡量的——例如，1 月/2 月/3 月的销售额与 4 月/5 月/6 月的销售额。

直觉非常简单——我测量处理组的变化，然后减去对照组观察到的任何变化，以期隔离由处理专门引起的变化。我不需要相信我的两组是相同的，但我确实需要相信它们的销售趋势在处理前是相互跟随的，并且在没有处理的情况下也会继续如此——这就是平行趋势假设。

df_sales_combined = pd.concat([df_sales_treat, df_sales_control])  
df_sales_combined["Year"] = df_sales_combined["Date"].dt.isocalendar().year  
df_sales_combined["Week"] = df_sales_combined["Date"].dt.isocalendar().week  
df_weekly_sales = df_sales_combined.groupby(["Group", "Year", "Week"]).agg({'Sales':'sum', 'Date':'first'}).reset_index()comp_start = (  df_weekly_sales  .query("Group == 'Treat' and Year==2013 and Date.dt.month==4")  .Date  .min()  
)start_date = comp_start - DateOffset(months=3)  
end_date   = comp_start + DateOffset(months=3)df_weekly_sales = df_weekly_sales[  (df_weekly_sales.Date >= start_date) &  (df_weekly_sales.Date <= end_date)  
]sns.set(style='whitegrid', font_scale=1.1)  
plt.figure(figsize=(12,5))ax = sns.lineplot(  data=df_weekly_sales,  x='Date',  y='Sales',  hue='Group',  palette=['#4C72B0','#55A868'],  linewidth=1.5  
)ax.yaxis.set_major_formatter(  ticker.StrMethodFormatter('{x:,.0f}')  
)plt.axvline(comp_start, color="red", linestyle="--", label="Competition Start")  
plt.legend()plt.title('Weekly Sales: Control vs Treatment')  
plt.xlabel('Week')  
plt.ylabel('Weekly Sales')  
plt.legend(title='')  
plt.tight_layout()  
plt.show()

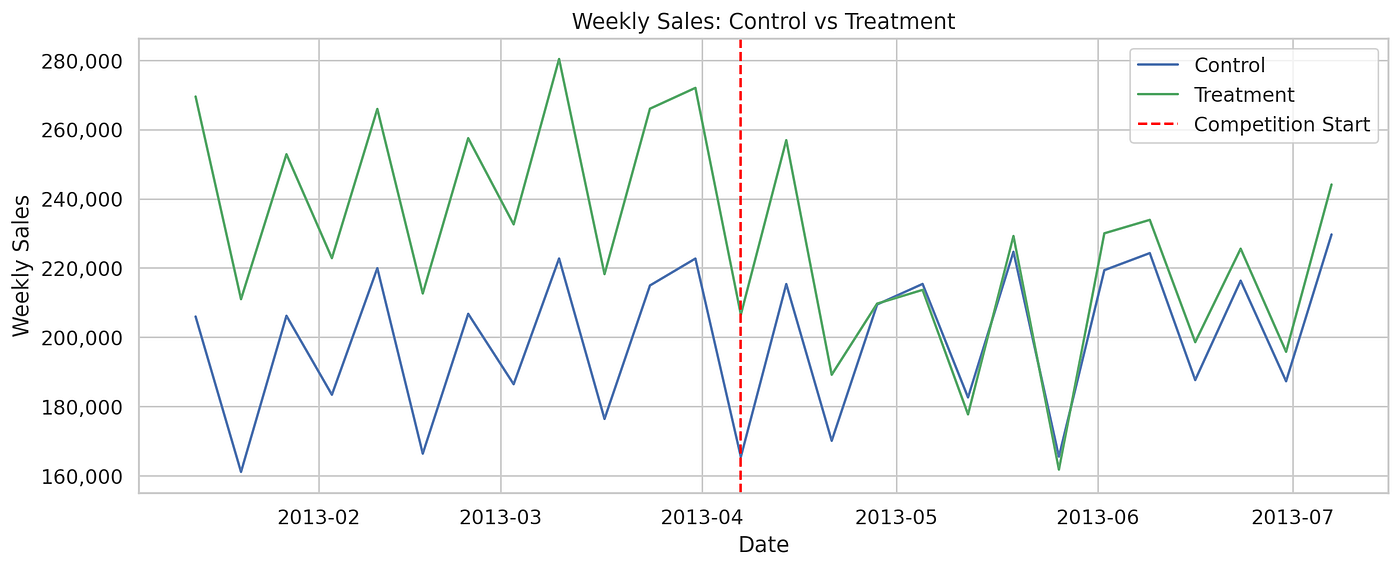
这看起来不错——在处理之前，趋势是相互跟随的。那么，让我们计算双重差分：

df = df_sales_combined.copy()  
df['Post'] = (df['Date'] >= comp_start).astype(int)  
df['Treat'] = (df['Group']=='Treatment').astype(int)  
df['Year_week'] = df.apply(lambda row: str(row['Year']) + str(row['Week']), 1)df_did = df.groupby(["Group", "Post"]).agg({'Sales':'mean'}).reset_index()did = (  df_did.loc[(df_did['Group'] == 'Treatment') & (df_did['Post'] == 1), 'Sales'].item() -   df_did.loc[(df_did['Group'] == 'Treatment') & (df_did['Post'] == 0), 'Sales'].item()  
) - (  df_did.loc[(df_did['Group'] == 'Control') & (df_did['Post'] == 1), 'Sales'].item() -   df_did.loc[(df_did['Group'] == 'Control') & (df_did['Post'] == 0), 'Sales'].item()  
)

这告诉我，平均而言，竞争对手在附近开业使我每家门店每周损失 1,498.76 英镑。

但是……这显著吗？我对这个效应有多确定？

1.1 作为回归问题的双重差分法

为了得到这些答案，DiD 实际上被公式化为一个回归问题。一个标准的线性回归模型将因变量（例如销售额）的值建模为一个或多个自变量（$x_1,x_2$ 等）的线性组合加上一个随机误差项 ($ϵ$)。

$y_i={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip}+{ϵ}_i$

$y_i$ 是第 $i$ 个观测值的因变量值，$x_{i1}$ 是第 $i$ 个观测值的 $x_1$ 自变量值，依此类推。每个 $\beta$ 系数告诉我们其自变量对因变量的贡献程度。普通最小二乘法 (OLS) 提供了一个 解析解，称为正规方程——它是测量的 $x$ 和 $y$ 值的函数——以最小化残差平方和（预测值和实际 $y$ 值之间的距离）的方式估计每个系数。同样的方法也为我们提供了一个公式，用于 估计每个系数的标准误差，它是残差和 $x$ 值的函数。

对于 DiD，回归公式是：

$y_i={\beta }_0+{\beta }_1({\text{Treated}}_i)+{\beta }_2({\text{Period}}_i)+{\beta }_3({\text{Treated}}_i\times {\text{Period}}_i)+{ϵ}_i$

这里，${\text{Treated}}_i$ 是一个虚拟变量，如果观测值在处理组中则为 1，如果在对照组中则为 0；${\text{Period}}_i$ 是一个虚拟变量，如果观测值在处理后时期则为 1，如果在处理前时期则为 0。

我们可以为此运行一个简单的 OLS 回归：

import statsmodels.formula.api as smfmodel = smf.ols('Sales ~ Treat*Post', data=df).fit()display(model.summary().tables[1])

Sales ~ Treat*Post 是一个简写，表示 Treat、Post 和 Treat*Post 都是感兴趣的 $x$ 变量。

结果是……

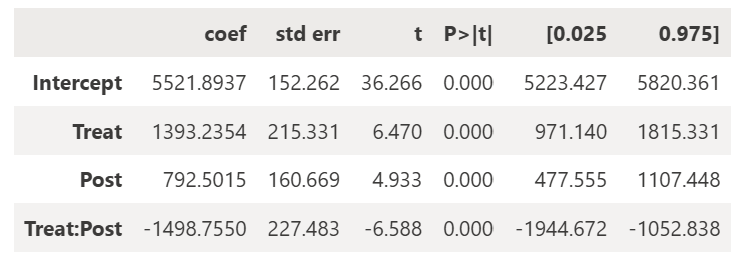
${\hat{\beta }}_3$ 项与我之前的 DiD 计算结果完全相同！这是因为当线性回归只包含虚拟变量时，估计的 $\hat{\beta }$ 系数就是相关分组的均值。所以我们可以通过将正确的 1 和 0 代入上面的回归公式，用估计的 $\hat{\beta }$ 系数来表示我们简单的 DiD 计算。（注意：Medium 似乎不允许我在符号上加上帽子，所以请将 $\hat{\beta }$ 理解为真实但未知的 $\beta$ 的估计量）。

$\text{DiD}=[(\text{处理组处理后平均销售额})-(\text{处理组处理前平均销售额})]-[(\text{对照组处理后平均销售额})-(\text{对照组处理前平均销售额})]$

$\text{DiD}=[({\hat{\beta }}_0+{\hat{\beta }}_1+{\hat{\beta }}_2+{\hat{\beta }}_3)-({\hat{\beta }}_0+{\hat{\beta }}_1)]-[({\hat{\beta }}_0+{\hat{\beta }}_2)-({\hat{\beta }}_0)]$

$\text{DiD}={\hat{\beta }}_3$

太棒了——所以我们知道处理的平均效应（附近竞争对手开业），而且我们也知道这一项的标准误差。

标准误差估计了估计系数的理论抽样分布的标准差。也就是说，如果我能够多次重复我的实验，使用相同的 $x$ 值，由于随机噪声 $ϵ$，我将得到一系列估计的 $\beta$ 值，而标准误差估计了这种分布的标准差。

标准误差反过来导致了置信区间的计算，这是一个值范围，如果我多次重复实验，它将在 95% 的时间里包含真实值。换句话说，它给出了系数的合理值范围。

OLS 回归带有一个 t 检验和相关的 p 值，这告诉我我的结果是显著的。很好！

1.2 观测值关联：聚类标准误差

这一切都好得有点不真实。一个复杂之处在于，普通的线性回归有许多必要的假设，其中最重要的一点是每个观测值都是独立的。（或者，具体地说，每个观测值的误差项与其他任何误差项都不相关，并且总是具有相同的方差。）但这对于我们来说并非如此。在我们上面的回归中，每个观测值都是特定门店在特定一周的数据。我们显然期望同一门店的不同观测值可能存在关联——上周表现最好的门店很可能下周仍然是表现最好的门店之一。

解决这个问题的方法是聚类标准误差。这种方法要求我们识别相关观测值的聚类——在我们的例子中是门店。估计标准误差的简单公式让位给一个 更通用的公式，该公式在聚类级别对残差进行聚合，然后将它们相加。

model = smf.ols('Sales ~ Treat*Post', data=df).fit(cov_type='cluster', cov_kwds={'groups': df['Store']})display(model.summary().tables[1])

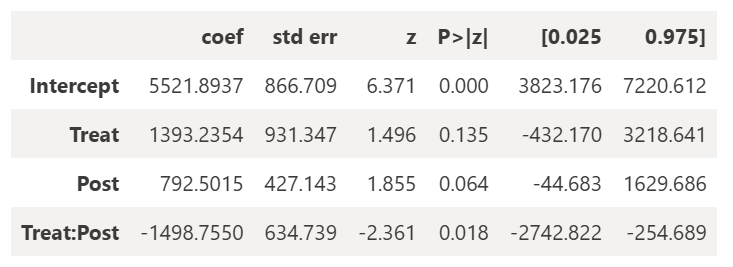
我的 ${\hat{\beta }}_3$ 估计量仍然相同——这是因为线性系数的估计仅取决于 $x$ 和 $y$ 值，而不取决于残差，因此不受任何聚类影响。但我的标准误差却飙升了。这就是聚类标准误差的目的——避免严重高估显著性。

1.3 固定效应

目前的回归假定了一个共同的 ${\beta }_0$ 截距——即每家门店都有相同的基线销售额，然后仅根据我们处于处理前还是处理后时期以及竞争对手是否在附近开业进行调整。这似乎不对，所以我们可以为门店添加一个固定效应。这实质上意味着为每家门店添加一个虚拟变量，这实际上导致每家门店都有自己的截距（基线销售额）。我们还可以为销售周添加一个固定效应——因为每周的销售基线也可能因季节性而异。

model = smf.ols('Sales ~ Treat*Post + C(Store) + C(Year_week)', data=df).fit(  cov_type='cluster', cov_kwds={'groups': df['Store']}  
)  
display(model.summary().tables[1])

您会看到大量关于各种门店和周的系数，但重要的系数如上所示。我的交互项现在略有变化。这是因为我的新固定效应解释了门店之间和时间之间基线销售额的一些系统性变异。

2 贝叶斯-双重差分法

上面的一切都符合频率学派的观点。在这个统计学领域中，我们完全依赖于我们的数据样本来估计我们感兴趣的事物。在这种情况下，感兴趣的事物是我们的回归系数 ${\beta }_3$。我们相信存在一个真实但不可知的 ${\beta }_3$，我们使用函数 ${\hat{\beta }}_3$（再次抱歉，帽子有点偏）来估计它。${\hat{\beta }}_3$ 是一个随机变量，因为它是由随机样本计算出来的，并且由于数据生成过程的随机噪声，每次都会取不同的值，但 ${\beta }_3$ 本身是固定的。

在贝叶斯统计中，${\beta }_3$ 本身被视为一个随机变量。这并不是因为我们认为物理数据生成过程每次运行实验都会改变，而仅仅是为了直接编码我们对其值的不确定性。因此，即使我们可能仍然相信存在一个真实但不可知的 ${\beta }_3$ 单一值，我们也会给 ${\beta }_3$ 自己的概率分布来表示我们目前对其的理解。如果我们对 ${\beta }_3$ 的值非常确定，那么我们将有一个非常尖锐的分布；如果我们一无所知，我们将有一个非常宽泛的分布。

这实际上有用的原因是我们可以使用贝叶斯定理。它有几种不同的形式——取决于我们谈论的是单个事件、连续函数等——但为了我们的目的，我们将使用：

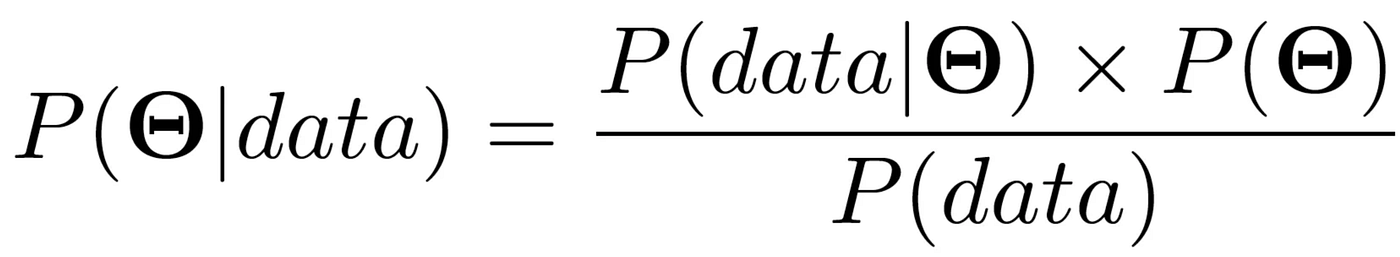
这里的大写 $\Theta$ (theta) 代表感兴趣的参数。所以对于我们的回归，它将是一个包含我们 $\beta$ 系数的向量。然后每个项是：

• $P(\Theta )$ —— 这是我们感兴趣参数的先验概率密度函数 (PDF)。它编码了我们对这些参数的先验信念。例如，如果我确定 ${\beta }_3$ 将是负数，我可以从只包含负数的先验分布开始。
• $P(\Theta |\text{data})$ —— 这是我们的后验分布。它是我们感兴趣参数的一个新分布函数，根据我们收集到的数据进行了更新。
• $P(\text{data}|\Theta )$ —— 这是我们的似然。它是一个 PDF，它告诉我对于我的 $\Theta$ 参数的每个可能值，我刚刚观察到的数据发生的概率。这是更新我的信念的关键——如果我的先验认为 ${\beta }_3$ 极有可能接近 -100，但我的似然说我的数据在这样的 ${\beta }_3$ 值下几乎不可能发生，那么我的后验将对 ${\beta }_3$ 接近 -100 的信心大大降低。
• $P(\text{data})$ —— 这是边际似然，一个归一化常数，表示观察到数据的概率，无论我的参数实际是什么。它等同于分子在所有可能的 $\Theta$ 值上的积分。

在上述所有情况中，我需要决定我认为了解物理现实的模型。对于我们来说，它是一个带有虚拟变量回归量和未知 $\beta$ 系数的线性回归；对于抛硬币来说，它将是一个带有单个未知参数的伯努利方程，等等。

所有这一切的重点是，我们可以利用我们现有的知识，而不是完全依赖数据，并且每次收集新数据时都可以更新我们的信念。也许明年会有一批新的竞争对手开业，我将使用今年的后验作为明年的先验。

2.1 定义贝叶斯模型

import pymc as pm  
import arviz as az  
import numpy as npdf['store_idx'] = df['Store'].astype('category').cat.codes  
df['week_idx']  = df['Year_week'].astype('category').cat.codesn_store = df['store_idx'].nunique()  
n_week  = df['week_idx'].nunique()with pm.Model() as did_bayes:  sigma_store = pm.HalfNormal('sigma_store', sigma=1000)  sigma_week  = pm.HalfNormal('sigma_week', sigma=1000)  sigma_res   = pm.HalfNormal('sigma_res', sigma=1000)intercept_store = pm.Normal('intercept_store', mu=0, sigma=sigma_store, shape=n_store)  intercept_week  = pm.Normal('intercept_week', mu=0, sigma=sigma_week,  shape=n_week)beta_treat     = pm.Normal('beta_treat', mu=0, sigma=1000)  beta_post      = pm.Normal('beta_post',  mu=0, sigma=1000)  beta_treatpost = pm.Normal('beta_treatpost', mu=0, sigma=1000)  mu = (  intercept_store[df['store_idx']]  + intercept_week[df['week_idx']]  + beta_treat * df['Treat']  + beta_post  * df['Post']  + beta_treatpost * df['Treat'] * df['Post']  )y_obs = pm.Normal('y_obs', mu=mu, sigma=sigma_res, observed=df['Sales'])

上面代码的第一个（有趣）部分定义了我们提到的所有先验。$\beta$ 先验非常直接——我们对这些 $\beta$ 值可能是什么没有真正的先验知识，所以我们一开始给每个值相同的正态分布。

更复杂的部分涉及个体门店和时间效应。以前，我们将这些视为额外的固定效应，旨在为每家门店和每周找到一个基线销售值。这种方法将每家门店和每周都视为完全独立的，如果我在分析中关心探究这些个体截距，这是必要的。

另一种包含不同门店和周效应的方法是将它们建模为随机效应。这里的直觉是，也许我不想创建一个只适用于我数据集中指定门店的模型，我想要创建一个适用于任何门店的模型——所以我需要将门店选择的效应视为一个随机变量。换句话说，我们仍然接受给定门店有自己的“截距”或基线销售额，但我们不将其视为要估计的固定参数，而是将其视为从概率分布中提取的效应。

在这里使用随机效应的关键假设是门店特定的效应与我的固定效应（例如，是否属于处理组）是独立的。一个混杂变量可能会扰乱这一点——例如，如果处于人流量大的区域既影响门店特定的基线销售额，又使其更有可能附近有竞争对手开业。

这引出了超先验的概念。我们为每个门店效应赋予了一个正态先验分布，但我们说这个先验分布的方差参数不是一个单一值，而实际上是另一个概率分布。超先验是另一个先验中参数的先验。

所有这些先验概念的一个有用结果是一个层次结构，其中所有门店都有自己的截距分布，但这些分布都受到全局 sigma_store 变量的影响。例如，如果我想获得给定门店具有特定截距 $a$ 的先验概率，我需要计算：

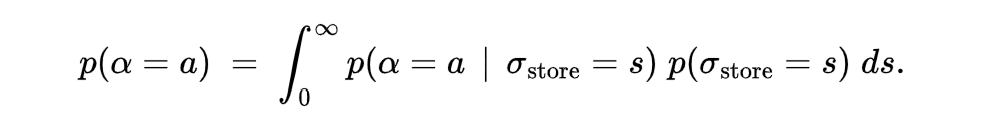
因为 sigma_store 和给定的 intercept_store 分布是内在相关的，所以它们在估计每个门店截距的联合后验时会同时更新。最终结果是，我们维护一个全局 sigma_store 分布，它反映了我们对门店之间差异的信念，以及一组个体 intercept_store 分布。这样做的好处是，如果 sigma_store 了解到门店之间存在真正的巨大差异，那么门店截距的后验将更多地由其自身数据驱动；但如果 sigma_store 了解到门店之间差异很小，那么每个门店截距的后验将趋向于全局均值。如果一家门店有大量数据，它将更能使其截距分布偏离其先验。这被称为部分池化。

顺便提一下，随机效应也可以包含在频率学派方法中。每家门店都被认为有一个从全局（正态）分布中提取的随机效应。任何给定门店的特定截距都由其自身数据驱动，向全局均值池化的程度由估计的全局方差（其本身由数据估计）决定。

2.2 创建后验分布

由于贝叶斯定理中的分母，后验分布通常过于复杂而无法解析计算，因此它们通常使用马尔可夫链蒙特卡洛 (MCMC) 采样构建。这涉及为我们感兴趣的参数创建一系列随机提议值。提议值与当前值的相对概率通过考虑该值的似然（即，如果这些参数为真，我们看到的数据发生的概率）和参数值的先验概率来计算。这个分数决定了我们接受链中这一步的可能性。换句话说，我们随机遍历贝叶斯定理的分子，在概率高的空间中花费更多的时间。这个过程将我们的后验分布构建为有效接受参数值的直方图。

with did_bayes:  trace = pm.sample(  draws=2000,  tune=1000,  chains=1,  target_accept=0.95,  random_seed=42,  return_inferencedata=True  )az.summary(  trace,  var_names=['beta_treatpost','sigma_store','sigma_week','sigma_res'],  round_to=2  
)

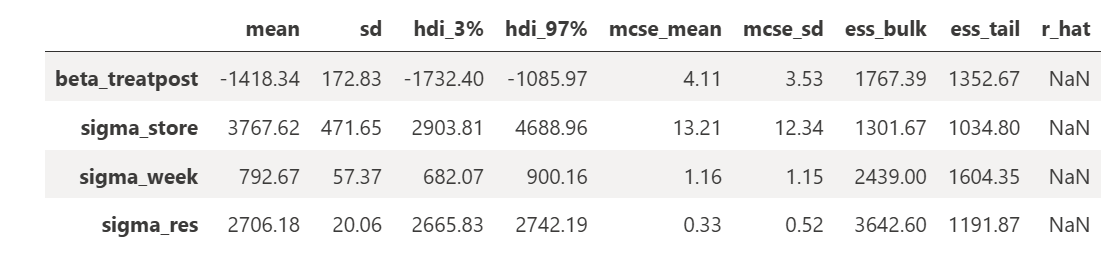
我的最终结果与我的 ${\beta }_3$ 项非常相似：-1418 对比频率学派方法的 -1467。我的 95% 可信区间——包含后验中 95% 概率质量的值范围——为 -1758 到 -1075。尽管它不能直接与置信区间进行比较，但有趣的是它在这种情况下更紧密。

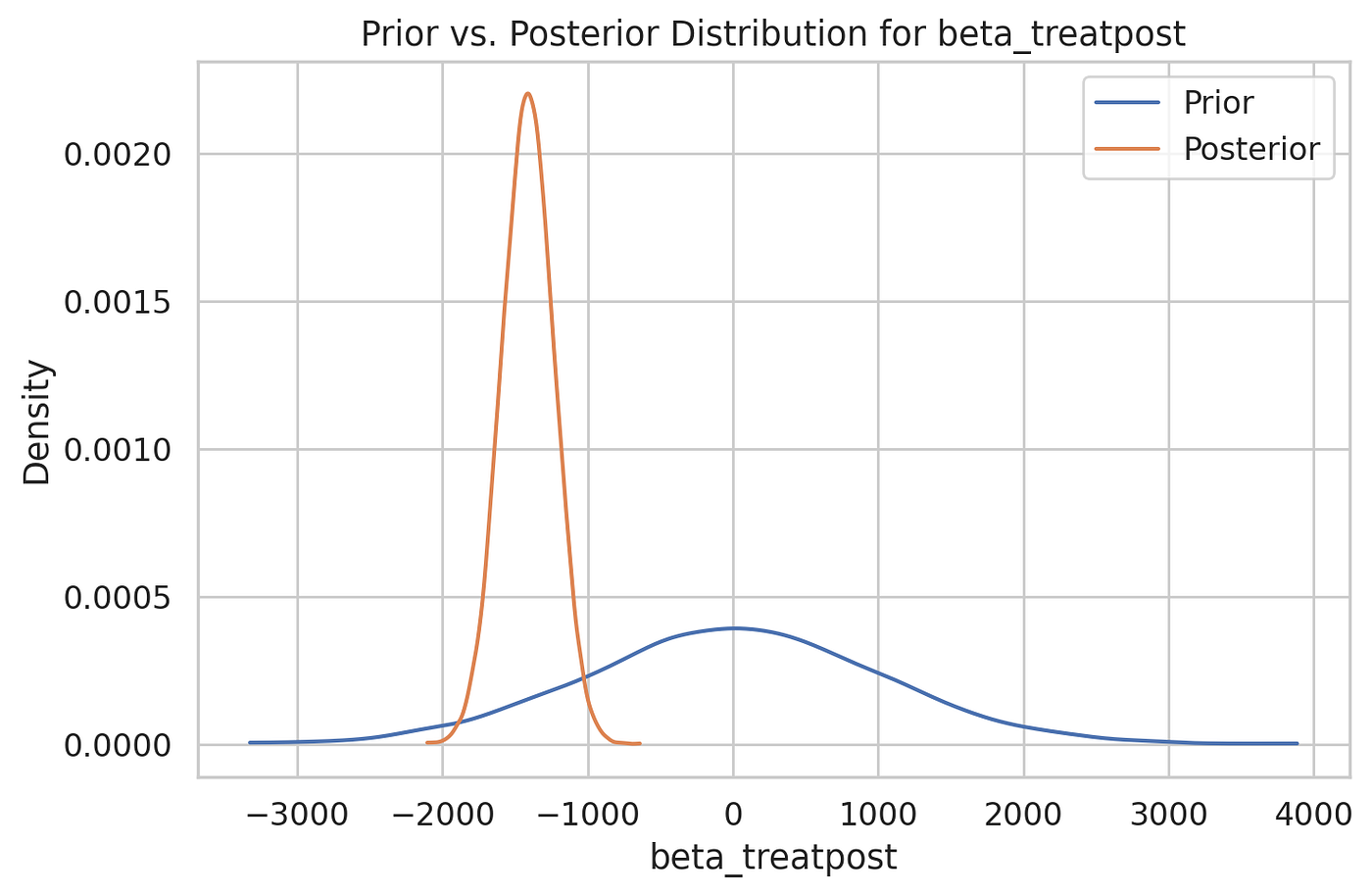
感兴趣参数 ${\beta }_3$ 的先验（蓝色）和更新后的后验。

3 方差分析 (ANOVA) 和协方差分析 (ANCOVA)

作为快速的后记，我想提一下方差分析 (ANOVA) 和协方差分析 (ANCOVA) 在这一切中的位置。这些术语经常在比较组的一般主题中被提及。

方差分析 (ANOVA) 是一种统计检验，通过比较组间方差与组内方差（F 统计量），来确定两个或多个不同组的均值是否显著不同。对于我们的场景，我们将研究重复测量方差分析，它用于在不同条件（时间与处理）下多次测量相同受试者（门店）的情况。

虽然方差分析通常被视为一种简单的统计检验，但它在幕后是线性回归的一个特例。重复测量方差分析是我们最初研究双重差分法时建模的线性回归的一个特例——其中我们有一个组间因素（处理组与对照组）和一个组内因素（处理前与处理后）。方差分析方法也将有一个交互项，它与我的 ${\hat{\beta }}_3$ 估计量相同。然而，将问题更普遍地视为回归任务，可以提供更大的灵活性——例如通过聚类标准误差和包含额外的固定效应或随机效应。

协方差分析 (ANCOVA) 再次是一种特定的回归方法。当我们有一个或多个分类变量和一个或多个连续协变量时使用。在这种情况下，分类变量将是处理组与对照组，连续协变量将是处理前销售额。所以这是一种略有不同的问题框架，其适用性取决于我试图实现的目标。协方差分析更关注确定处理后组间均值是否存在差异，并利用处理前销售额来辅助，而不是专门量化处理影响的大小。

此外，协方差分析在非随机实验中更容易遇到困难，因为它假设协变量（处理前销售额）与组分配（处理组与对照组）是独立的——在我们的例子中，我们认为这可能不成立，因此我们探讨了聚类标准误差和固定效应。