当前位置：首页 > news >正文

量化交易 - Stochastic Gradient Descent Regression (SGDRegressor) 随机梯度下降回归 - 机器学习

news 2025/9/20 7:30:07

一、构造数据及SGDRegressor拟合

二、还原参数

一、构造数据及SGDRegressor拟合

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler# 1. 造数据 build data
x = np.linspace(-5, 50, 100)
# y = β1 + β1 * x + ε
y = 50 + 2 * x + np.random.normal(0, 20, size=len(x))
data = pd.DataFrame({'X': x, 'Y': y})# 2. 画图 plot data
ax = data.plot.scatter(x='X', y='Y', figsize=(14, 6))
sns.despine()
plt.tight_layout()
plt.show()# 3. 标准化 standardize data
scaler = StandardScaler()
X_ = scaler.fit_transform(data[['X']])# 4. 训练 train model
# Scikit-learn <=1.2: squared_loss;  Scikit-learn >=1.3: squared_error
sgd = SGDRegressor(loss='squared_error',  fit_intercept=True,shuffle=True,random_state=42,learning_rate='invscaling',eta0=0.01,power_t=0.25)sgd.fit(X_, data['Y'].values)# 5. 预测并画图 predict and plot
# x_plot = np.linspace(-5, 50, 300).reshape(-1, 1)
x_plot = x.reshape(-1, 1)
x_plot_scaled = scaler.transform(x_plot)
y_pred = sgd.predict(x_plot_scaled)plt.figure(figsize=(14, 6))
plt.scatter(data['X'], data['Y'], label='raw')
plt.plot(x_plot, y_pred, color='red', label='SGD fit')
sns.despine()
plt.legend()
plt.show()# 6. 参数  get model parameters
print("coef (scaled):", sgd.coef_[0])
print("intercept:", sgd.intercept_)

针对SGDRegressor的解释：

sgd = SGDRegressor(loss='squared_loss',      # 使用平方误差损失（即普通线性回归）fit_intercept=True,       # 是否拟合截距项（bias）shuffle=True,             # 每次epoch前打乱样本顺序random_state=42,          # 保证结果可复现learning_rate='invscaling',  # 学习率随时间递减：eta = eta0 / (t^power_t)eta0=0.01,                # 初始学习率power_t=0.25              # 控制学习率下降速度
)

同时注意：Scikit-learn <=1.2: squared_loss; Scikit-learn >=1.3: squared_error

使用squared_loss或者squared_error其实就是OLS，线性回归。

另外，使用SGDRegressor的话，需要先对数据进行标准化处理，再进行训练拟合。

原始数据：

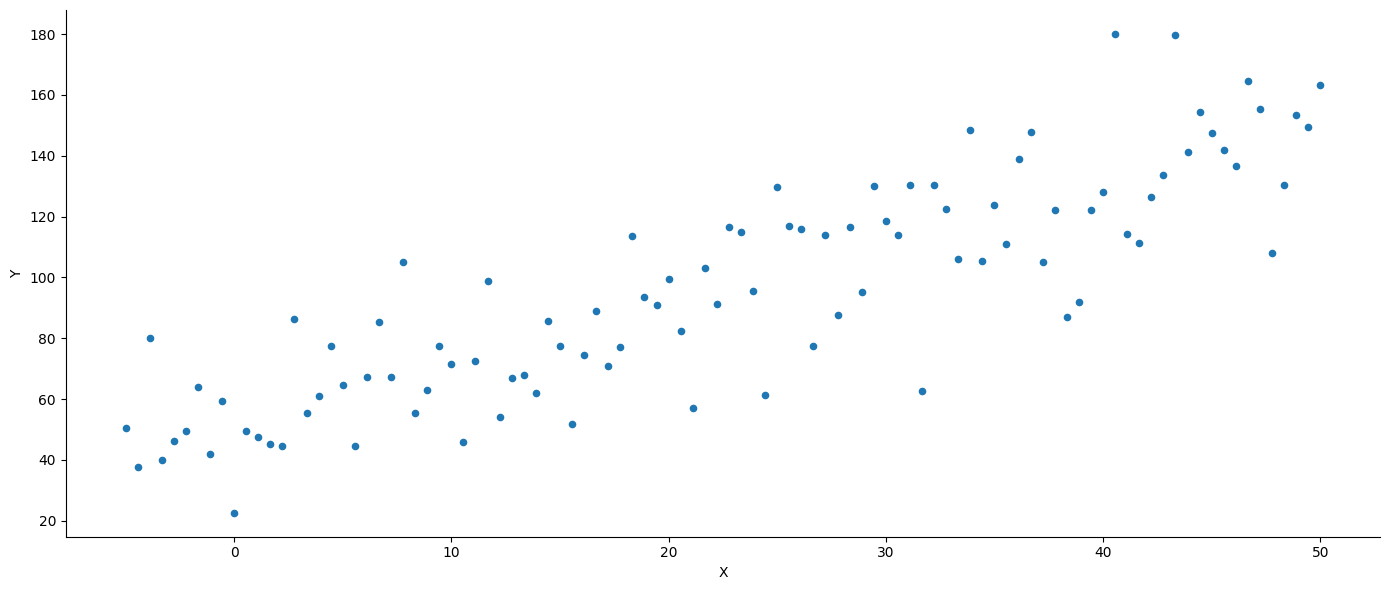
拟合曲线

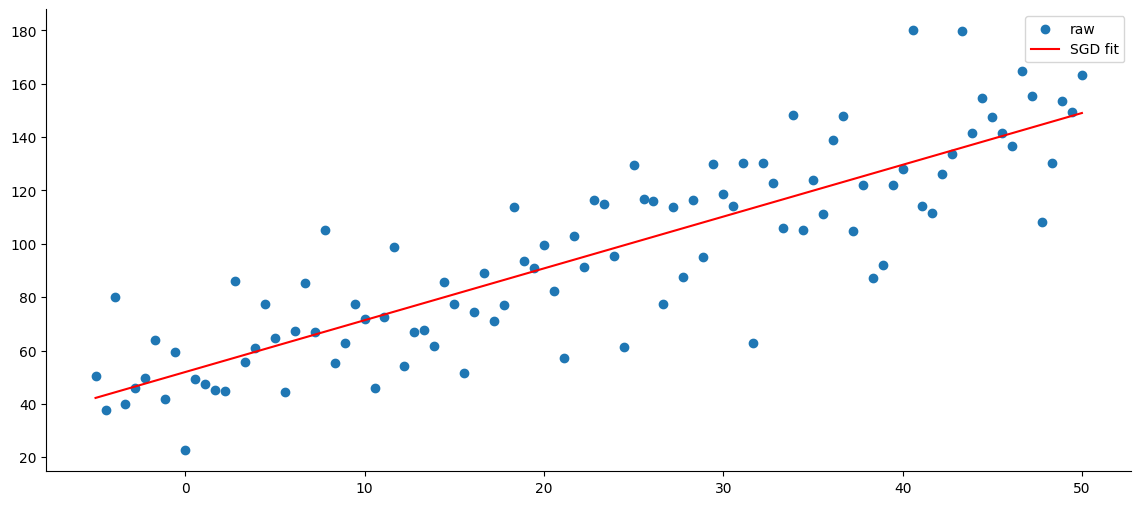
coef (scaled): 31.146794886625532

intercept: [95.63400611]

可以发现，是不同于原始参数的，所以我们需要还原

二、还原参数

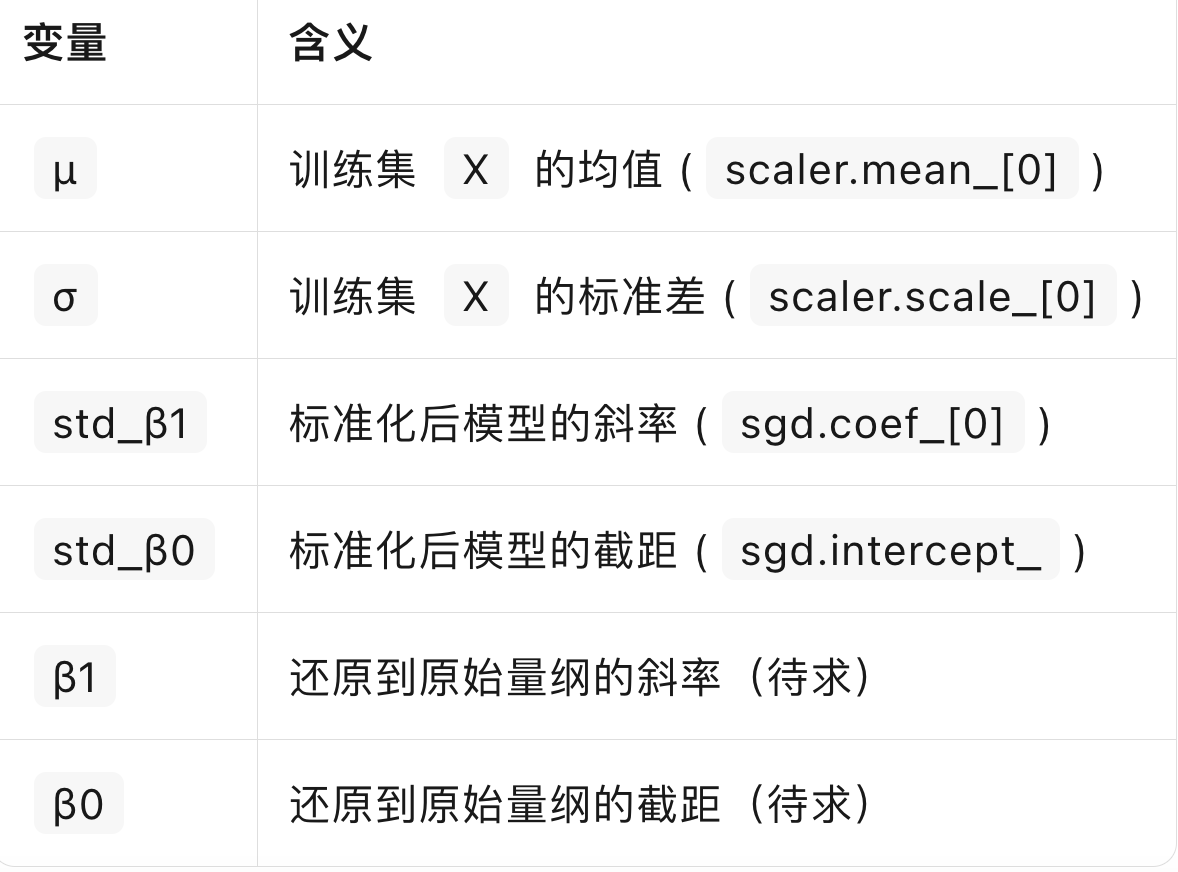
推导过程

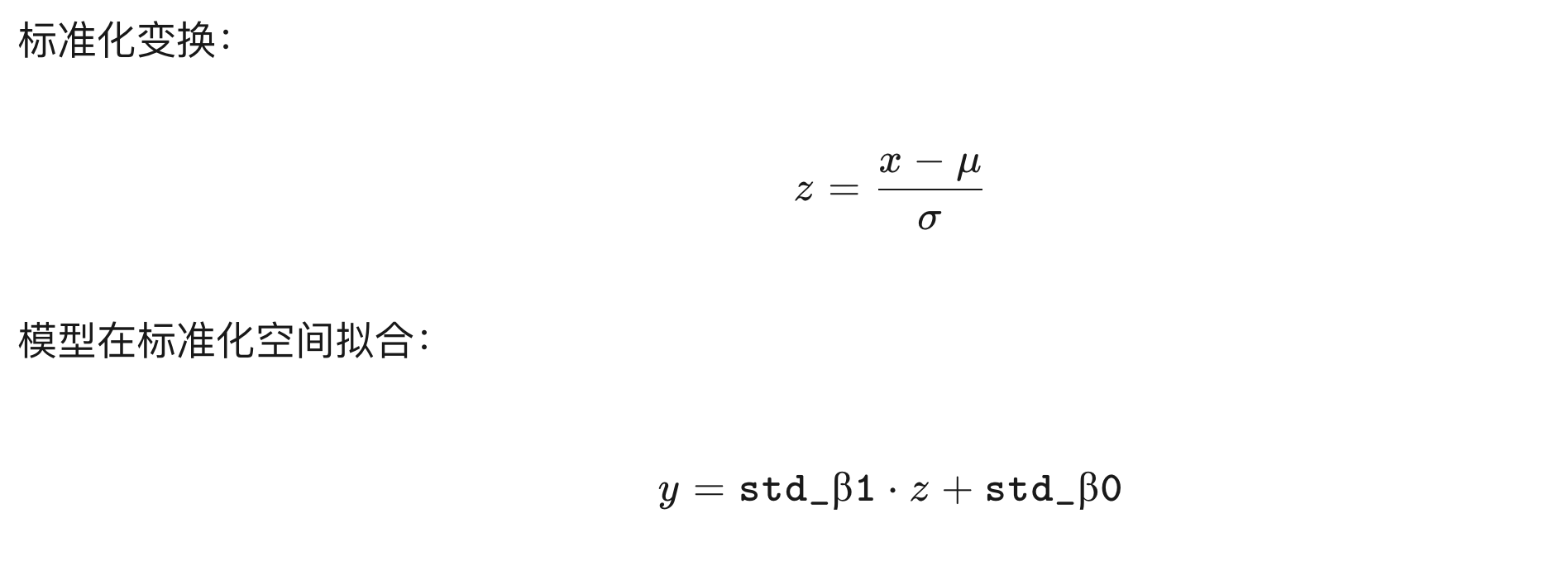
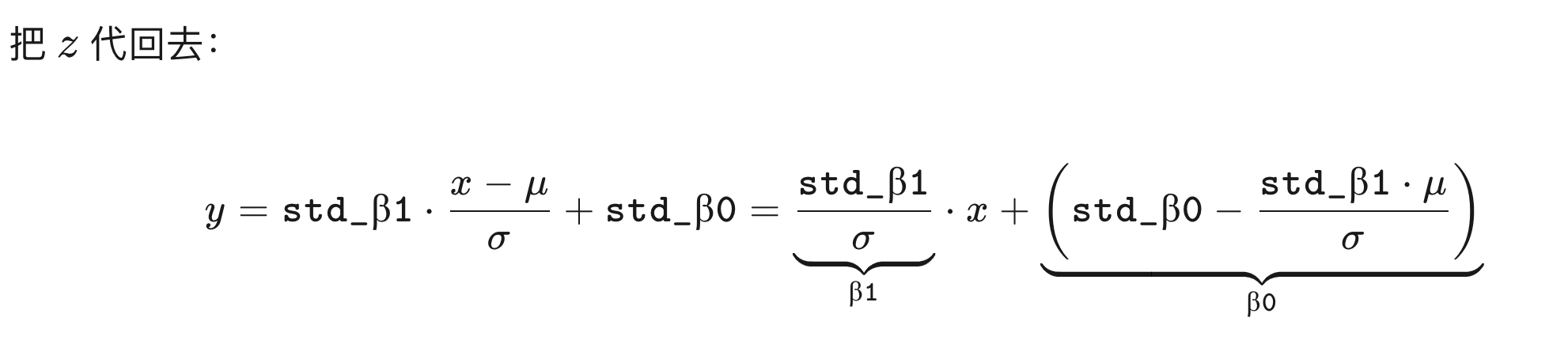
所以，

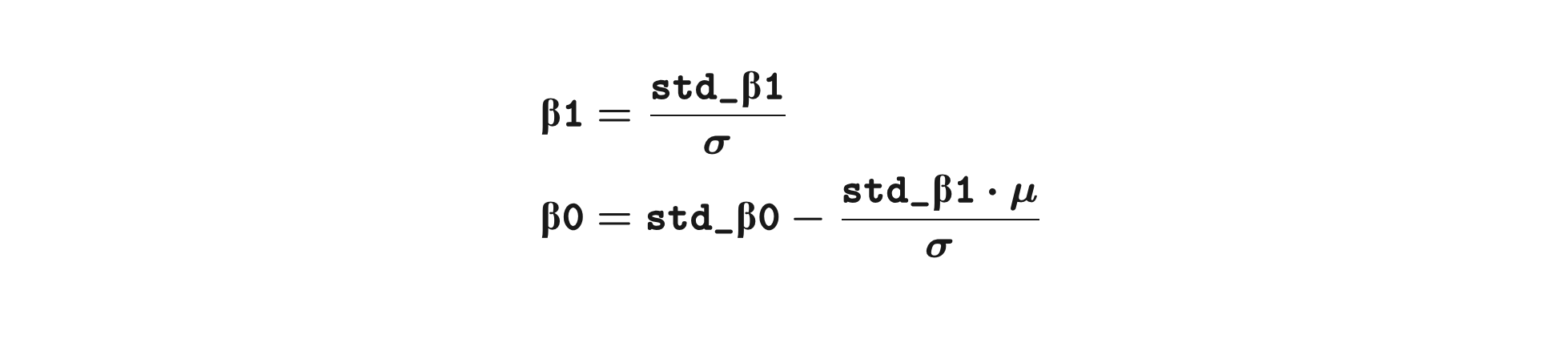
用代码计算：

μ = scaler.mean_[0]      # 均值             mean
σ = scaler.scale_[0]     # 标准差           standard deviation (std)
std_β1 = sgd.coef_[0]         # 标准化后的斜率    coefficient (slope)
std_β0 = sgd.intercept_       # 标准化后的截距    interceptβ1 = std_β1 / σ
β0 = std_β0 - std_β1 * μ / σprint("β1:", β1)
print("β0:", β0)

β1: 1.9422190378960196

β0: [51.93407775]

这样和原始数据就很接近了。

参考并改进：

# Reference: https://github.com/stefan-jansen/machine-learning-for-trading/blob/main/07_linear_models/01_linear_regression_intro.ipynb

查看全文

http://www.dtcms.com/a/391008.html