当前位置： 首页 > news >正文

【数据结构】堆的概念

news 2025/9/20 6:40:30

一、堆的概念与性质

01 堆的概念

堆(Heap)是计算机科学中一类特殊的数据结构。堆通常是一个可以被看作一棵完全二树的数组对象，若满足：

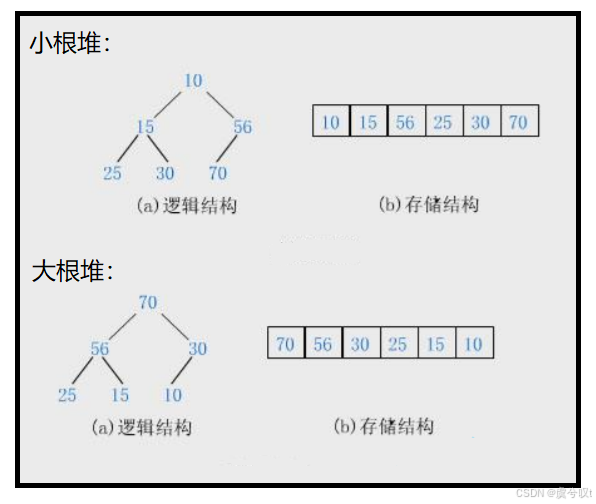
  • 任意节点的值>=其子节点的值。则称为大根堆。
  • 任意节点的值<=其子节点的值。则称为小根堆。

综上所述：

大根堆：树中任何一棵树及子树中，父亲的值都大于等于孩子 
小根堆：树中任何一颗树及子树中，父亲的值都小于等于孩子 
 

02 堆的性质

① 堆总是一棵完全二叉树。

② 堆中的某个节点的值总是不大于或不小于其父节点的值。

03 堆的作用

① 堆排序

② 解决 TopK 问题

二、堆的定义

01 数组堆

所有的数组都可以表示成完全二叉树，但是它不一定是堆。

  • 大堆：树中所有父亲都大于等于孩子。
  • 小堆：树中所有父亲都小于等于孩子。

代码演示：实现大堆

typedef int HPDataType;typedef struct Heap {HPDataType* array;int size;int capacity;
} HP;

02 接口函数

这是需要实现几个接口函数：

/* 堆的初始化 */
void HeapInit(HP* php);/* 堆的销毁 */
void HeapDestroy(HP* php);/* 堆的打印 */
void HeapPrint(HP* php);/* 判断堆是否为空 */
bool HeapIsEmpty(HP* hp);/* 堆的插入 */
void HeapPush(HP* php, HPDataType x);/* 检查容量 */
void HeapCheckCapacity(HP* php);/* 交换函数 */
void Swap(HPDataType* px, HPDataType* py);/* 大根堆上调 */
void AdjustUp(int* arr, int child);/* 堆的删除 */
void HeapPop(HP* php);/* 大根堆下调 */
void AdjustDown(int* arr, int n, int parent);/* 返回堆顶数据*/
HPDataType HeapTop(HP* php);/* 统计堆的个数 */
int HeapSize(HP* php);

三、堆的实现

01 初始化（HeapInit）

Heap.h：

/* 堆的初始化 */
void HeapInit(HP* php);

Heap.c：

/* 堆的初始化 */
void HeapInit(HP* php) {assert(php);php->array = NULL;php->size = php->capacity = 0;
}

02 销毁（HeapDestory）

Heap.h：

/* 堆的销毁 */
void HeapDestroy(HP* php);

Heap.c：

/* 堆的销毁 */
void HeapDestroy(HP* php) {assert(php);free(php->array);php->size = php->capacity = 0;
}

03 打印（HeapPrint）

Heap.h：

/* 堆的打印 */
void HeapPrint(HP* php);

Heap.c：

/* 堆的打印 */
void HeapPrint(HP* php) {for (int i = 0; i < php->size; ++i) {printf("%d ", php->array[i]);}printf("\n");
}

04 判断堆是否为空（HeapIsEmpty）

Heap.h：

/* 判断堆是否为空 */
bool HeapIsEmpty(HP* php);

Heap.c：

/* 判断堆是否为空 */
bool HeapIsEmpty(HP* php) {assert(php);return php->size == 0;
}

05 检查是否需要增容（HeapCheckCapacity）

Heap.h：

/* 检查容量 */
void HeapCheckCapacity(HP* php);

Heap.c：

/* 检查容量 */
void HeapCheckCapacity(HP* php) {if (php->size == php->capacity) {int new_capacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp_array = (HPDataType*)realloc(php->array, sizeof(HPDataType) * new_capacity);if (tmp_array == NULL) {printf("realloc failed");exit(-1);}php->array = tmp_array;php->capacity = new_capacity;}
}

06 堆的插入（HeapPush）

插入的核心思路：

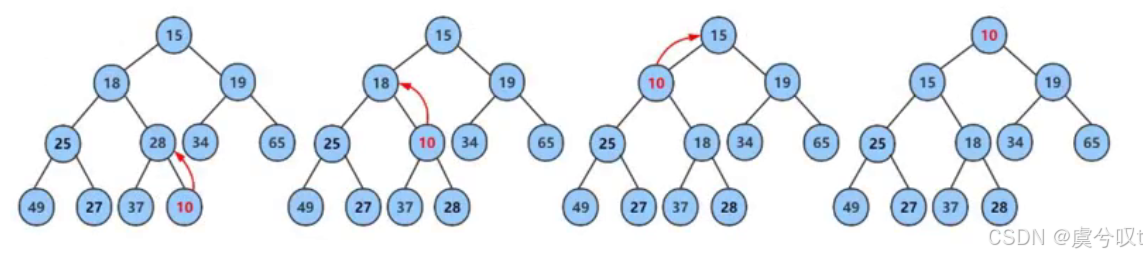
① 先将元素插入到堆的末尾，即最后一个孩子之后。

② 插入之后如果堆的性质遭到破坏，就将新插入的节点顺着其父亲往上调整到合适位置。直到调整到符合堆的性质为止。

根据堆的性质，如果不满足大堆和小堆，出现子大于父或父大于子的情况，为了保证插入之后堆还是堆，我们就需要进行自下往上的调整。堆插入数据对其他节点没有影响，只是可能会影响从它到根节点路径上节点的关系。

举例：

① 比如下面的情况：新插入的为 60，子大于父（60 > 56），这时就需要交换。

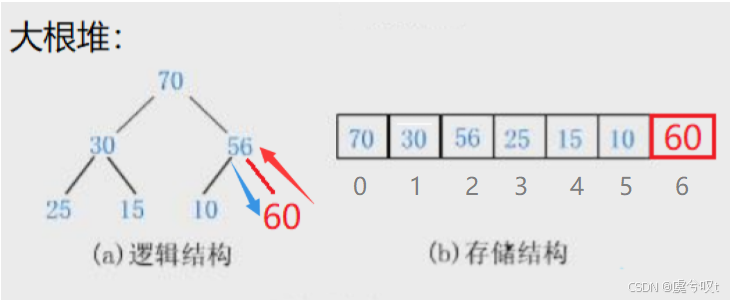
② 还有更特殊的情况：比如新插入的为 100，100 和 56 交换完之后还要和 70 交换。

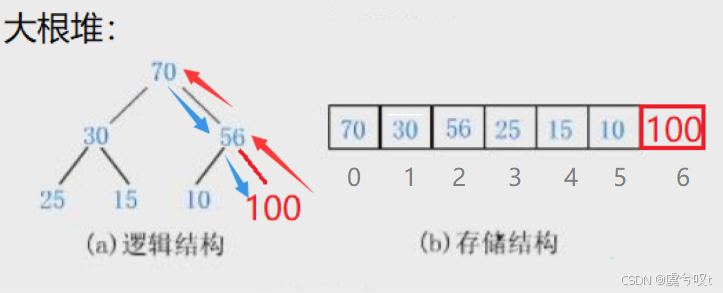
先把父亲赋值给孩子，再把孩子赋值给父亲，再让父亲往上走，判断是否比父亲大，如果大就再进行交换。 为了搞定这些情况，我们就需要写一个 "向上调整" 的算法（最坏调到根停止）：

Heap.h：

/* 堆的插入 */
void HeapPush(HP* php, HPDataType x);/* 大根堆上调 */
void AdjustUp(int* arr, int child);

Heap.c：

/* 大根堆上调 */
void AdjustUp(int* arr, int child) {assert(arr);// 根据公式算出父亲的下标int father = (child - 1) / 2;// 最坏情况:调到根，child == father当 child 为根节点时结束（根节点永远是0）while (child > 0) {if (arr[child] > arr[father]) {HPDataType tmp = arr[child];arr[child] = arr[father];arr[father] = tmp;// 往上走child = father;father = (child - 1) / 2;}else {break;}}
}

这里我们用到了交换，因为后面写删除接口也是需要用到交换的，

我们不妨把它封装成一个接口，方便我们后续可以多次调用：

void Swap(HPDataType* px, HPDataType* py) {HPDataType tmp = *px;*px = *py;*py = tmp;
}
/* 堆的插入 */
void HeapPush(HP* php, HPDataType x) {assert(php);// 检查是否需要扩容HeapCheckCapacity(php);// 插入数据php->array[php->size] = x;php->size++;// 向上调整AdjustUp(php->array, php->size - 1);
}

07 堆的删除（HeapPop）

删除的核心思路：删除堆，删除的是堆顶的数据。就是删除这个树的根。

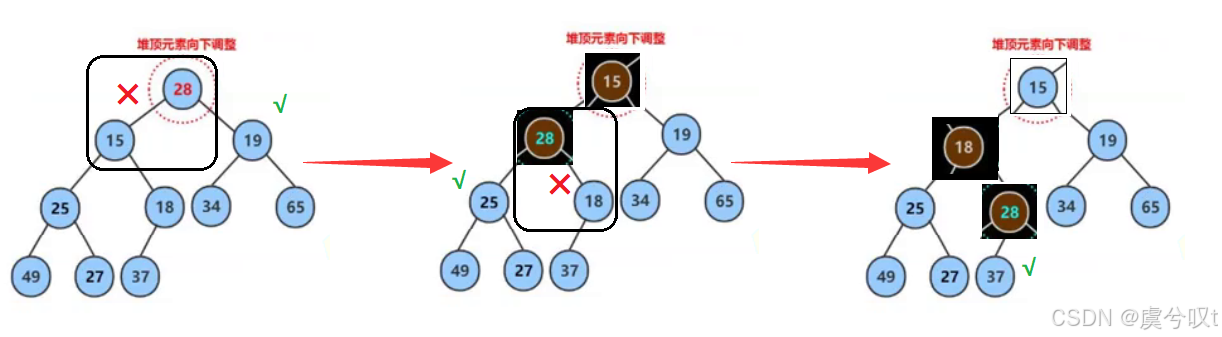
将堆顶的数据跟最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

Heap.h：

/* 堆的删除 */
void HeapPop(HP* php);/* 大根堆下调 */
void AdjustDown(int* arr, int n, int parent);

Heap.c：

/* 大根堆下调 */
void AdjustDown(int* arr, int n, int parent) {// 默认为左孩子int child = parent * 2 + 1;while (child < n) {if (child + 1 > n && arr[child + 1] > arr[child]) {child = child + 1;}if (arr[child] > arr[parent]) {Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}
/* 堆的删除 */
void HeapPop(HP* php) {assert(php);assert(!HeapIsEmpty(php));Swap(&php->array[0], &php->array[php->size - 1]);php->size--;AdjustDown(php->array, php->size, 0);
}

08 获取堆顶数据（HeapTop）

Heap.h：

/* 返回堆顶数据*/
HPDataType HeapTop(HP* php);

Heap.c：

/* 返回堆顶数据*/
HPDataType HeapTop(HP* php) {assert(php);assert(!HeapIsEmpty(php));return php->array[0];
}

09 统计堆的元素个数（HeapSize）

Heap.h：

/* 统计堆的个数 */
int HeapSize(HP* php);

Heap.c：

/* 统计堆的个数 */
int HeapSize(HP* php) {assert(php);return php->size;
}

四、完整代码

Heap.h：

#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>typedef int HPDataType;typedef struct Heap {HPDataType* array;int size;int capacity;
} HP;/* 堆的初始化 */
void HeapInit(HP* php);/* 堆的销毁 */
void HeapDestroy(HP* php);/* 堆的打印 */
void HeapPrint(HP* php);/* 判断堆是否为空 */
bool HeapIsEmpty(HP* hp);/* 堆的插入 */
void HeapPush(HP* php, HPDataType x);/* 检查容量 */
void HeapCheckCapacity(HP* php);/* 交换函数 */
void Swap(HPDataType* px, HPDataType* py);/* 大根堆上调 */
void AdjustUp(int* arr, int child);/* 堆的删除 */
void HeapPop(HP* php);/* 大根堆下调 */
void AdjustDown(int* arr, int n, int parent);/* 返回堆顶数据*/
HPDataType HeapTop(HP* php);/* 统计堆的个数 */
int HeapSize(HP* php);

Heap.c：

#include "Heap.h"/* 堆的初始化 */
void HeapInit(HP* php) {assert(php);php->array = NULL;php->size = php->capacity = 0;
}/* 堆的销毁 */
void HeapDestroy(HP* php) {assert(php);free(php->array);php->size = php->capacity = 0;
}/* 堆的打印 */
void HeapPrint(HP* php) {for (int i = 0; i < php->size; ++i) {printf("%d ", php->array[i]);}printf("\n");
}/* 判断堆是否为空 */
bool HeapIsEmpty(HP* php) {assert(php);return php->size == 0;
}/* 检查容量 */
void HeapCheckCapacity(HP* php) {if (php->size == php->capacity) {int new_capacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp_array = (HPDataType*)realloc(php->array, sizeof(HPDataType) * new_capacity);if (tmp_array == NULL) {printf("realloc failed");exit(-1);}php->array = tmp_array;php->capacity = new_capacity;}
}void Swap(HPDataType* px, HPDataType* py) {HPDataType tmp = *px;*px = *py;*py = tmp;
}/* 大根堆上调 */
void AdjustUp(int* arr, int child) {assert(arr);// 根据公式算出父亲的下标int father = (child - 1) / 2;// 最坏情况:调到根，child == father当 child 为根节点时结束（根节点永远是0）while (child > 0) {if (arr[child] > arr[father]) {//HPDataType tmp = arr[child];//arr[child] = arr[father];//arr[father] = tmp;Swap(&arr[child], &arr[father]);// 往上走child = father;father = (child - 1) / 2;}else {break;}}
}/* 堆的插入 */
void HeapPush(HP* php, HPDataType x) {assert(php);// 检查是否需要扩容HeapCheckCapacity(php);// 插入数据php->array[php->size] = x;php->size++;// 向上调整AdjustUp(php->array, php->size - 1);
}/* 大根堆下调 */
void AdjustDown(int* arr, int n, int parent) {// 默认为左孩子int child = parent * 2 + 1;while (child < n) {if (child + 1 > n && arr[child + 1] > arr[child]) {child = child + 1;}if (arr[child] > arr[parent]) {Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}/* 堆的删除 */
void HeapPop(HP* php) {assert(php);assert(!HeapIsEmpty(php));Swap(&php->array[0], &php->array[php->size - 1]);php->size--;AdjustDown(php->array, php->size, 0);
}/* 返回堆顶数据*/
HPDataType HeapTop(HP* php) {assert(php);assert(!HeapIsEmpty(php));return php->array[0];
}/* 统计堆的个数 */
int HeapSize(HP* php) {assert(php);return php->size;
}

http://www.dtcms.com/a/390807.html

相关文章：

  • STL 简介：C++ 标准库的 “瑞士军刀”
  • 数据结构 静态链表的实现(算法篇)
  • [新启航]燃料喷射孔孔深光学 3D 轮廓测量 - 激光频率梳 3D 轮廓技术
  • Python 数据分析详解（第一期）：环境搭建与核心库基础
  • 云手机中混合架构具体是什么？
  • 设计模式-桥接模式详解
  • Web 抓包全指南 Web抓包工具、浏览器抓包方法、HTTPS 解密
  • 在Prompt IDE中编写提示词时，如何确保提示词的质量和效果？
  • OpenCV ：基于 Lucas-Kanade 算法的视频光流估计实现
  • PyQt6之容器布局
  • Linux网络：HTTPS协议
  • 【Linux】进程概念(三)：深入剖析操作系统学科的进程状态理论体系与 Linux 系统下的浅度睡眠、深度睡眠、停止、僵尸、死亡等具体进程状态
  • java面试Day2 | mysql优化、索引、事务、并发事务、MVCC、主从同步、分库分表
  • 怎么用文字生成视频：从本土到海外的软件工具选择指南
  • Git远程与本地仓库关联指南（含推送冲突解决方案）
  • uniapp u-popup弹窗展示时禁止底部内容滚动，禁止滑动遮罩层滚动
  • 赛灵思 XCVU13P-2FIGD2104E XilinxFPGA VirtexUltraScale+
  • 基于非线性MPC的自动驾驶路径跟踪与避障控制器设计(Matlab实现)
  • 使用云手机进行烈火一刀挂机多开的优势
  • 造成云手机黑屏的原因有哪些？
  • 智能电视玩机攻略_开启设备隐藏ADB 自由安装第三方应用
  • 微服务项目-＞在线oj系统(Java-Spring)----2.0
  • Swift闭包使用详情
  • STM32，新手学习
  • 保险丝Fuse
  • Kafka的持久化及副本机制总结
  • c() 函数在 R 中的用途详解
  • 使用Rsync+sersync实现数据实时同步
  • 关于conda forge长时间solving的问题以及如何解决
  • 前端学习手册-JavaScript基础语法(十)