当前位置：首页 > news >正文

数据结构静态链表的实现(算法篇)

news 2025/9/20 6:39:22

1. 链表

1.1 链表的定义

1.2 链表的分类

2. 静态链表

2.1 定义静态单链表

2.2 创建静态单链表

2.3 头插

2.4 遍历静态单链表

2.5 补充:

2.6 按值查找

2.7 在任意位置之后插⼊元素

2.8 删除任意位置之后的元素

2.9 测试所有代码

3. 双向静态链表

3.1 定义

编辑

2.2 头插

2.3 遍历函数

2.4 按值查找

2.5 在任意位置之后插⼊元素

2.6 在任意位置之前插⼊元素

2.7 删除任意位置的元素

2.8 测试所有代码

4. 循环链表的模拟实现

5. 总结:

1. 链表

1.1 链表的定义

线性表的链式存储就是链表。
它是将元素存储在物理上任意的存储单元中，由于无法像顺序表一样通过下标保证数据元素之间的逻辑关系，链式存储除了要保存数据元素外，还需额外维护数据元素之间的逻辑关系，这两部分信息合称结点（node）。即结点有两个域：保存数据元素的数据域和存储逻辑关系的指针域。

1.2 链表的分类

将各种类型的链表排列组合，总共有8种不同链表结构：

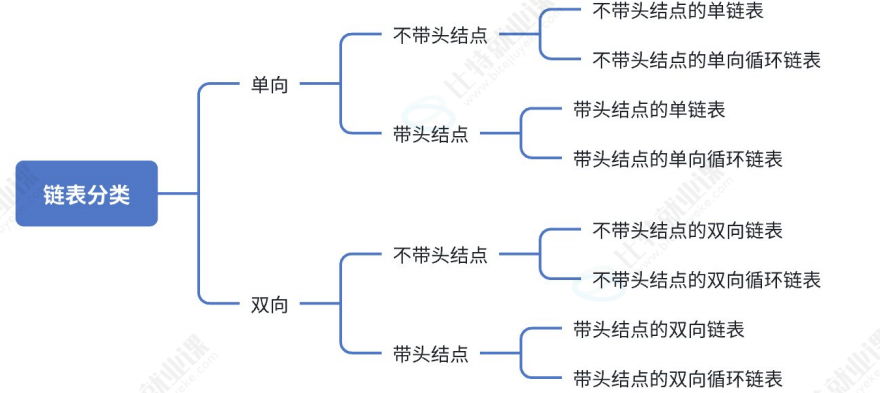
虽然链表种类较多，我们只需掌握单向链表，双向链表和循环链表即可，熟悉之后其他链表便可自行实现。

2. 静态链表

链表的实现方式分为动态实现和静态实现两种。

动态实现是通过 new 申请结点，然后通过 delete 释放结点的形式构造链表。这种实现方式最能体现链表的特性；
静态实现是利用两个数组配合来模拟链表。第一次接触可能比较抽象，但是它的运行速度很快，在算法竞赛中会经常会使用到。

本篇我们将着重讲解算法中常用到的静态链表

2.1 定义静态单链表

1. 两个足够大的数组，一个用来存数据，一个用来存下一个结点的位置

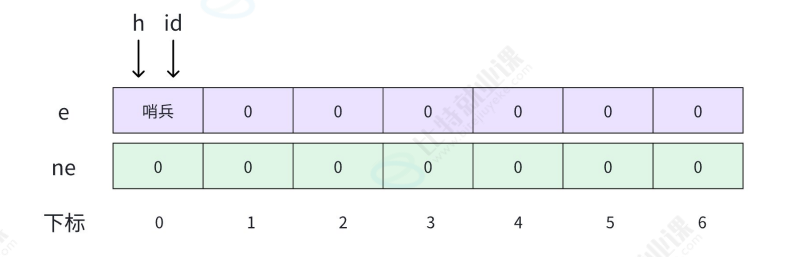
要理解这些概念，我们可以逐个拆解：

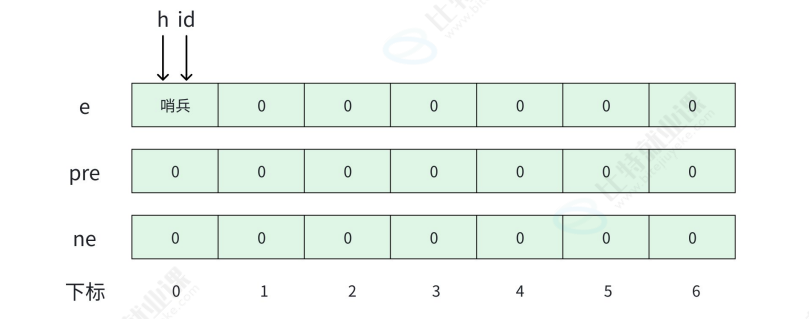
变量 h ：是头指针，它指向的是链表的起始位置（这里初始指向下标为0的“哨兵位”），通过它可以找到链表的第一个有效节点，是操作链表的入口。

变量 id ：用于为新节点分配数组下标（位置），每当要插入一个新节点时， id 会递增，指向接下来要使用的数组位置，确保新节点有地方存储数据和指针。

数组 e ：是数据域数组， e[下标] 存储的是对应节点的实际数据。比如 e[0] 是哨兵位的数据（示例中无实际意义），后续 e[1] 、 e[2] 等存储的是链表中有效节点的数据。

数组 ne ：是指针域数组， ne[下标] 存储的是下一个节点的数组下标（动态链表是指针）。例如 ne[0] = 0 表示哨兵位的下一个节点是自己（初始无有效节点时的逻辑），后续 ne[id] 会指向其他节点的下标，从而形成链式结构。

下标：是数组 e 和 ne 的索引，每个下标对应一个“逻辑节点”。下标0是哨兵位（不存有效数据，仅作逻辑锚点），下标1、2等是后续可能存储有效节点的位置， id 会管理这些下标分配， h 则通过下标指向链表的起始逻辑节点。

需要注意的是 : h 和 id 存储的都是数组的下标数字，用来标识节点在数组中的位置

头指针、哨兵位和普通节点的关系

要梳理头指针、哨兵位和普通节点的关系，我们可以从定义、作用、相互连接逻辑三个维度拆解：
1. 各自定义

头指针（ h ）：是一个变量，存储的是链表中第一个有效节点的位置（数组下标），用来标识链表的起始位置。
哨兵位：是数组中下标为 0  的位置（也可设为 -1  等，示例中默认用 0 ），它不存储有效数据，仅作为“逻辑锚点”存在。
普通节点：是链表中存储实际数据的单元，由 e[id] （数据域）和 ne[id] （指针域，存储下一个节点的位置）组成， id  是其在数组中的下标。

2. 核心作用

头指针 h ：通过它能快速找到链表的第一个有效节点，是操作链表的“入口”。
哨兵位：解决“空链表操作”的边界问题，让头插、删除等操作的代码逻辑更统一（无需单独处理空链表的特殊情况）。
普通节点：承载实际数据，通过 ne  数组的指针关系形成链式结构。

2.2 创建静态单链表

const int N = 1e5 + 10;int h; // 头指针
int id; // 下一个元素分配的位置
int e[N], ne[N]; // 数据域和指针域// 下标 0 位置作为哨兵位
// 其中 ne 数组全部初始化为 0，其中 ne[i] = 0 就表示空指针，后续没有结点
// 当然，也可以初始化为 -1 作为空指针，看个人爱好//e[i] 和 ne[i] 是绑定在一起使用的，也有一种写法是定义一个结构体，把这两个变量放在一起，比如：
struct node
{int e, ne;
}list[N];
/*但是，定义成结构体之后，代码书写不方便。我们只要知道 e[i] 和 ne[i] 是绑定在一起使用的即可
*/

1. 核心元素说明
数组与变量

const int N = 1e5 + 10; ：定义数组大小，适配算法竞赛中常见的数据规模。
int h; ：头指针，指向链表的起始位置（初始指向哨兵位）。
int id; ：用于为新节点分配数组下标，管理节点的“位置分配”。
int e[N], ne[N]; ： e  是数据域数组，存储节点的实际数据； ne  是指针域数组，存储下一个节点的数组下标，模拟链表的指针关系。

哨兵位

下标为 0  的位置作为哨兵位， ne  数组初始化为 0 （或 -1 ）表示空指针，其作用是简化空链表的操作逻辑，让头插、删除等操作无需单独处理边界情况。

结构体对比

代码中提到可以用结构体 struct node{int e, ne;}list[N];  来绑定数据域和指针域，但这种方式代码书写不够便捷，因此实际采用两个数组 e  和 ne  配合的方式，更适合算法竞赛中的快速实现。

2. 用途与场景
这种静态链表的实现方式常用于算法竞赛，其优势是运行速度快，能高效处理大规模数据的链式结构操作（如头插、删除等），同时避免了动态内存分配的开销与风险。

2.3 头插

这是链表中最常用也是使用最多的操作，后续树和图的存储中的邻接表以及链式前向星就会用到这个操作。因此必须要掌握的操作。

// 头插
void push_front(int x)
{// 先把 x 放在一个格子里面id++;e[id] = x;// 修改指针，顺序不能颠倒！// 1. x 的右指针指向哨兵位的后继// 2. 哨兵位的右指针指向 xne[id] = ne[h];ne[h] = id;
}

步骤	代码	说明
分配新节点位置	id++; e[id] = x	为新元素 x 分配数组下标 id ，并将 x 存入数据域数组 e 的对应位置
修改指针关系（顺序不可颠倒）	ne[id] = ne[h]	让新节点的指针域指向“哨兵位的后继节点”（即原链表的第一个有效节点）
	ne[h] = id	让哨兵位的指针域指向新节点，完成头插

时间复杂度:
仅涉及指针修改，时间复杂度为O(1)，效率很高。

2.4 遍历静态单链表

// 打印链表
void print()
{// 定义⼀个指针从头结点开始// 通过 ne 数组逐渐向后移动// 直到遇到空指针for (int i = ne[h]; i!=0; i = ne[i]){cout << e[i] << " ";}cout << endl << endl;
}

遍历逻辑:

从 ne[h]  开始（ h  是头指针，指向哨兵位， ne[h]  即为第一个有效节点的下标）。
通过循环赋值 i = ne[i]  不断后移指针，直到 i  为空指针（即 i == 0 ，因为示例中以 0  表示空指针）。
循环内打印当前节点的 e[i] （数据域），从而输出整个链表的所有有效数据。

时间复杂度:
遍历操作需要访问链表中每一个有效节点，因此时间复杂度为 O(N)（N 是链表的有效节点数）。

补充:

这段代码不会打印哨兵节点。因为循环的初始条件是 i = ne[h] （ h  是哨兵位下标0， ne[h]  指向的是第一个有效节点，而非哨兵位本身），后续也只遍历有效节点的 e[i] ，所以哨兵位的“占位数据”不会被打印出来。

2.5 补充:

h 是一个固定的数值（始终为0），对应哨兵位的数组下标，是链表操作的“锚点”。
id 是一个动态递增的数值，对应新节点的数组下标，每插入一个新节点， id 就会加1，为新节点分配唯一的存储位置。
这两个数值共同作用于 e （数据域数组）和 ne （指针域数组）对应的下标，通过下标将数据和指针关系“绑定”，从而模拟出链表的链式结构。

2.6 按值查找

链表的按值查找操作，有两种实现方法：

解法一（遍历法）：从链表的第一个有效节点开始，逐个遍历节点，对比数据域是否等于目标值 x 。遍历过程中，找到就返回该节点的下标，没找到就返回0。这种方法的时间复杂度是O(N)（N是链表节点数），适用于所有场景。

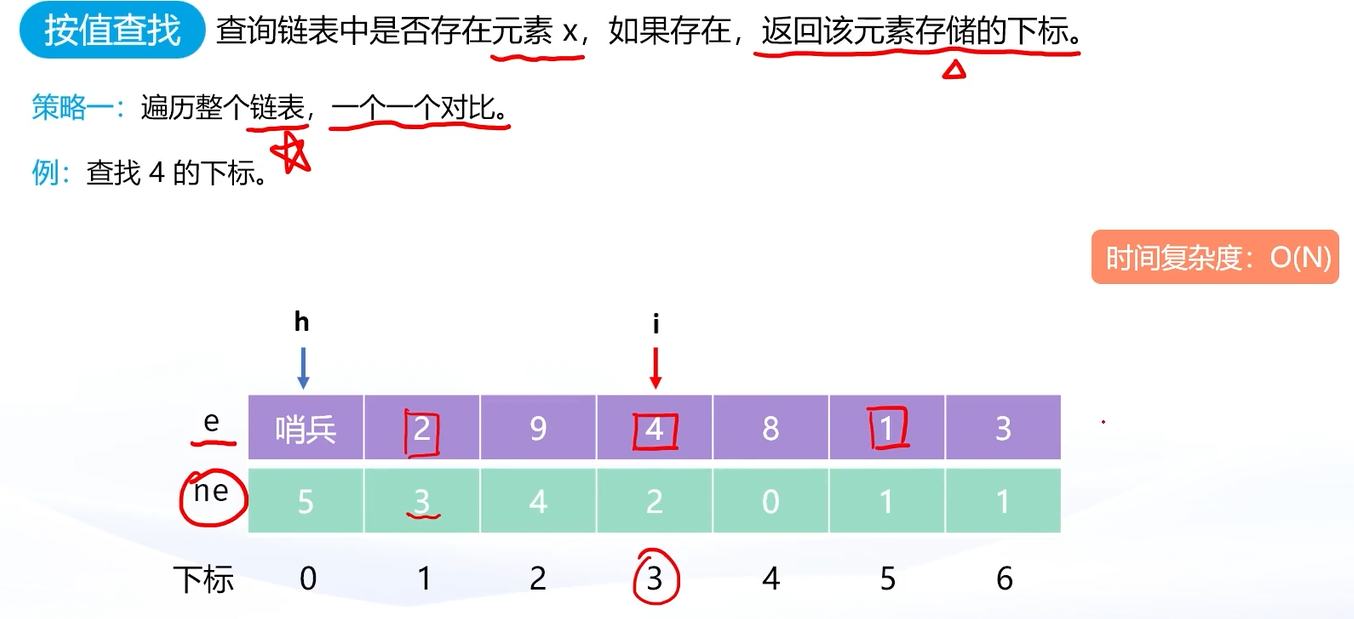
解法二（哈希表优化法）：用一个数组 mp 来记录元素值和其存储位置的映射。插入元素时，标记 mp[x] = id （ id 是节点下标）；删除元素时，清除 mp[x] 的标记；查询时，直接返回 mp[x] 即可。这种方法的时间复杂度是O(1)，但要求元素值的数据范围不大，属于“空间换时间”的优化策略。

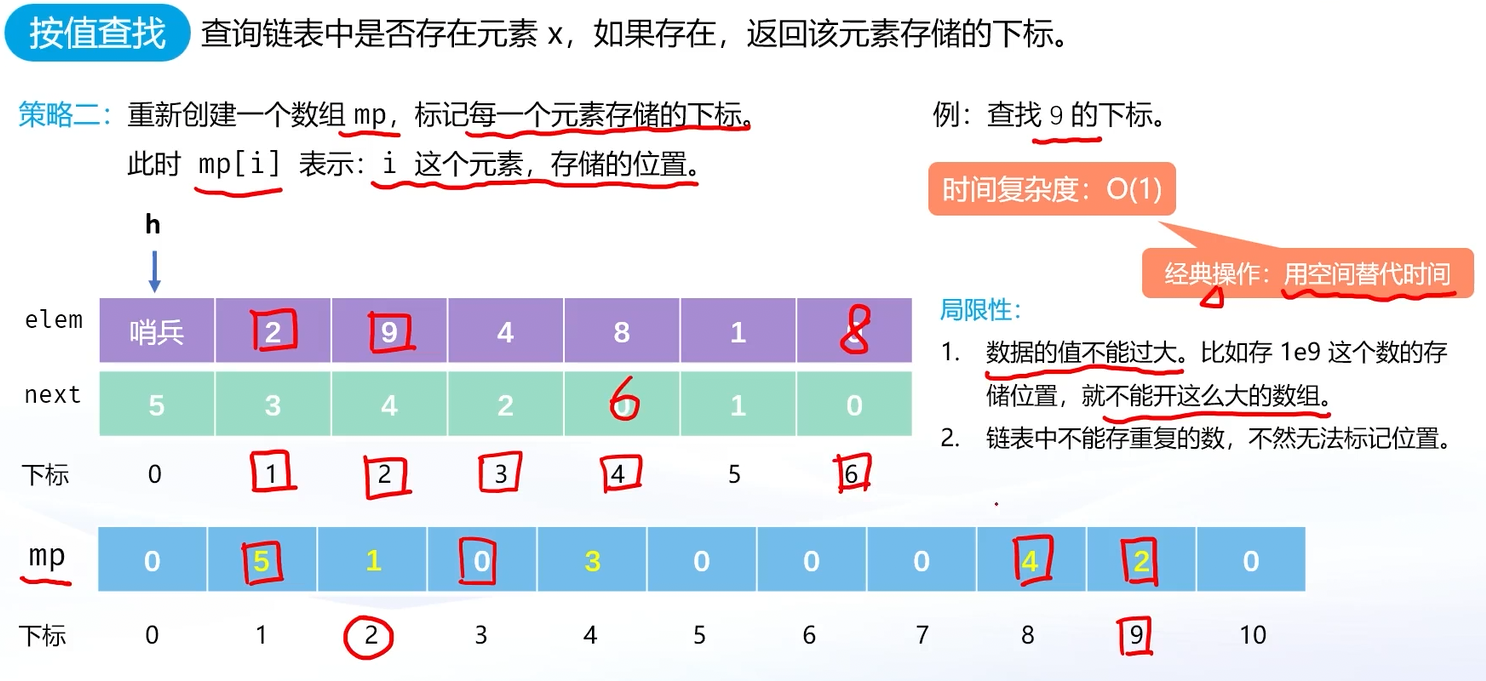
如果要用第二种方法 , 那我们在创建时就要这样创建:

int mp[N];    //mp[i]表示 i这个数存储的位置

查找代码为:

// 头插
void push_front(int x)
{id++;e[id] = x;mp[x] = id;// 先让新结点指向头结点的下一个位置// 然后让头结点指向新来的结点ne[id] = ne[h];ne[h] = id;
}// 按值查找
int find(int x)
{// /// 解法一：遍历链表// for(int i = ne[h]; i; i = ne[i])// {//     if(e[i] == x) return i;// }// return 0;// 解法二：用 mp 数组优化return mp[x];
}

1. 头插函数 push_front(int x)

mp[x] = id ：这是为了“按值查找”做的优化——用数组 mp  记录值 x  对应的节点下标 id ，后续查询时可以直接通过 mp[x]  快速找到节点位置。

2. 按值查找函数 find(int x)

解法一（遍历链表）：被注释掉了。逻辑是从第一个有效节点开始（ i = ne[h] ），逐个遍历节点，对比数据域 e[i]  是否等于 x ，找到则返回节点下标，没找到返回 0 。这种方法的时间复杂度是 O(N)（ N  是链表节点数）。
解法二（用 mp  数组优化）：直接返回 mp[x] 。因为头插时已经记录了 x  对应的节点下标，所以查询时可以直接通过 mp  数组得到位置，时间复杂度是 O(1)，效率更高（但要求元素值的范围不大，属于“空间换时间”的优化策略）。

头插时的 mp[x] = id  是为了给“按值查找”打标记，而 find  函数的解法二就是利用这个标记实现快速查询，两者配合让链表的按值查找操作从“遍历全表”优化为“直接查表”，体现了数据结构中“操作间的逻辑联动”和“时间-空间权衡”的设计思路。

2.7 在任意位置之后插⼊元素

// 在存储位置为 p 的元素后⾯，插⼊⼀个元素 x
void insert(int p, int x) // ⼀定要注意，这⾥的 p 是位置，不是元素
{id++; // x 这个元素分配的位置e[id] = x; // 将 x 放在 id 位置处ne[id] = ne[p]; // x 指向 p 的后⾯ne[p] = id; // p 指向 x
}

这是静态单链表中在指定位置 p  后插入元素 x  的实现代码：
1. 分配新节点

id++ ：为新元素 x  分配数组下标 id （即新节点的位置）。
e[id] = x ：将数据 x  存入新节点的数据域数组 e  中。

2. 建立指针（游标）关系

ne[id] = ne[p] ：让新节点的“游标”指向 p  节点原本的后继节点（即 p  后面的节点）。
ne[p] = id ：让 p  节点的“游标”指向新节点 id ，从而将新节点插入到 p  之后。

作用与特性:
该操作的时间复杂度是 O(1)，因为只需修改两个游标的指向，无需遍历链表。这种实现体现了静态链表“用数组下标模拟指针，实现高效插入”的核心优势，同时避免了动态链表的内存分配开销。

2.8 删除任意位置之后的元素

// 删除存储位置为 p 后⾯的元素
void erase(int p) // 注意 p 表⽰元素的位置
{if (ne[p]){mp[e[ne[p]]] = 0; // 将 p 后⾯的元素从 mp 中删除ne[p] = ne[ne[p]]; // 指向下⼀个元素的下⼀个元素}
}
这是一个静态单链表的删除操作函数 erase ，用于删除存储位置 p  后面的元素。
1. 函数逻辑

判断合法性： if (ne[p])  确保 p  后面存在可删除的元素（若 ne[p]  为 0  或无效值，说明无后继元素，不执行删除）。
从映射表中移除： mp[e[ne[p]]] = 0  是将 p  后面元素从辅助映射表 mp  中删除（若存在该映射逻辑，用于快速索引）。
修改游标关系： ne[p] = ne[ne[p]]  让 p  直接指向其“后继的后继”，从而跳过被删除的节点，完成逻辑删除。

2. 作用与特性
该操作的时间复杂度为 O(1)，只需修改游标和映射表即可完成删除，体现了静态链表“通过数组下标模拟指针，实现高效删除”的优势，同时避免了动态链表的内存释放开销。

为什么不像顺序表⼀样，实现⼀个尾插、尾删、删除任意位置的元素等操作？

能实现，但是没必要。因为时间复杂度是 O(N) 级别的。

使⽤各种数据结构是⽅便我们去解决问题的，⽽不是添堵（增加时间复杂度）的~

2.9 测试所有代码

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
// 创建
int e[N], ne[N], h, id;
int mp[N]; // mp[i] 表⽰ i 这个数存储的位置
// 遍历链表
void print()
{for (int i = ne[h]; i; i = ne[i]){cout << e[i] << " ";}cout << endl << endl;
}
// 头插
void push_front(int x)
{id++;e[id] = x;mp[x] = id; // 标记 x 存储的位置// 先让新结点指向头结点的下⼀个位置// 然后让头结点指向新来的结点ne[id] = ne[h];ne[h] = id;
}
// 按值查找
int find(int x)
{// // 解法⼀：遍历链表// for(int i = ne[h]; i; i = ne[i])// {// if(e[i] == x) return i;// }// return 0;// 解法⼆：⽤ mp 数组优化return mp[x];
}
// 在任意位置 p 之后，插⼊⼀个新的元素 x
void insert(int p, int x)
{id++;e[id] = x;mp[x] = id;ne[id] = ne[p];ne[p] = id;
}
// 删除任意位置 p 后⾯的元素
void erase(int p)
{if (ne[p]) // 当 p 不是最后⼀个元素的时候{mp[e[ne[p]]] = 0; // 把标记清空ne[p] = ne[ne[p]];}
}
int main()
{for (int i = 1; i <= 5; i++){push_front(i);print();}//cout << find(1) << endl;//cout << find(5) << endl;//cout << find(6) << endl;// insert(1, 10);// print();// insert(2, 100);// print();erase(2);print();erase(4);print();return 0;
}

3. 双向静态链表

双向链表⽆⾮就是在单链表的基础上加上⼀个指向前驱的指针，那就再来⼀个数组，充当指向前驱的指针域即可。

3.1 定义

const int N = 1e5 + 10;
int h; // 头结点
int id; // 下⼀个元素分配的位置
int e[N]; // 数据域
int pre[N], ne[N]; // 前后指针域
// h 默认等于 0，指向的就是哨兵位
// 此时链表为空，没有任何⼏点，因此 ne[h] = 0

2.2 头插

// 头插
void push_front(int x)
{id++;e[id] = x;mp[x] = id; // 存⼀下 x 这个元素的位置// 左指向哨兵位，右指向哨兵位的下⼀个位置，也就是头结点pre[id] = h;ne[id] = ne[h];// 先修改头结点的指针，再修改哨兵位，顺序不能颠倒pre[ne[h]] = id;ne[h] = id;
}
这是静态双向链表的头插函数 push_front ，用于在链表头部插入元素 x 。

1. 函数逻辑

分配新节点： id++ 为新元素 x 分配数组下标 id ，将 x 存入数据域数组 e[id] ，并通过映射表 mp 记录 x 的位置（ mp[x] = id ）。
建立双向指针关系：
pre[id] = h ：新节点的前驱指针指向哨兵位 h 。
ne[id] = ne[h] ：新节点的后继指针指向哨兵位原本的后继（即原头节点）。
更新原头节点和哨兵位的指针：
pre[ne[h]] = id ：原头节点的前驱指针指向新节点。
ne[h] = id ：哨兵位的后继指针指向新节点，完成头插。

2. 作用与特性
该函数实现了静态双向链表的头插操作，通过双向指针（ pre 前驱、 ne 后继）支持“向前/向后遍历”，同时利用映射表 mp 实现元素到位置的快速索引。操作时间复杂度为 O(1)，体现了静态链表高效插入的优势。

2.3 遍历函数

直接⽆视 prev 数组，与单链表的遍历⽅式⼀致。
// 打印链表
void print()
{for (int i = ne[h]; i; i = ne[i]){cout << e[i] << " ";}cout << endl << endl;
}
这是静态链表的遍历（打印）函数 print ，用于输出链表中的所有元素。

1. 函数逻辑

遍历起始：从哨兵位 h  的后继节点开始（ i = ne[h] ）。
遍历过程：通过 for  循环，每次将 i  更新为其后继节点的下标（ i = ne[i] ），直到 i  为 0 （或无效值）时结束。
元素输出：在循环中打印当前节点的数据域 e[i] 。

2. 特性与意义

该遍历方式与单链表的遍历逻辑一致，只需通过“游标数组 ne ”即可完成，可直接无视前驱数组 prev 。
时间复杂度为 O(N)（ N  为链表节点数），需遍历整个链表才能输出所有元素，体现了链表遍历的线性时间特性。

2.4 按值查找

// 查找元素 x 在链表中存储的位置
int find(int x)
{// ⽤ mp 优化return mp[x];
}
这是静态链表的按值查找函数 find ，用于快速查找元素 x 在链表中的存储位置。
1. 函数逻辑

利用映射数组 mp 实现“元素值 → 存储位置”的直接映射，调用 find 函数时，直接返回 mp[x] 即可得到元素 x 在链表中的下标位置。

2. 特性与意义

时间复杂度为 O(1)，通过映射数组实现了“常数时间”的查找，相比传统链表遍历查找（O(N)）效率大幅提升。
该优化体现了静态链表结合辅助结构（如映射数组）的灵活性，在需要频繁按值查找的场景中非常实用。

2.5 在任意位置之后插⼊元素

// 在存储位置为 p 的元素后⾯，插⼊⼀个元素 x
void insert_back(int p, int x)
{id++;e[id] = x;mp[x] = id; // 存⼀下 x 这个元素的位置// 先左指向 p，右指向 p 的后继pre[id] = p;ne[id] = ne[p];// 先让 p 的后继的左指针指向 id// 再让 p 的右指针指向 idpre[ne[p]] = id;ne[p] = id;
}
这是静态双向链表的“在任意位置之后插入元素”函数 insert_back ，用于在存储位置 p  之后插入元素 x 。
1. 函数逻辑

分配新节点： id++  为新元素 x  分配数组下标 id ，将 x  存入数据域数组 e[id] ，并通过映射表 mp  记录 x  的位置（ mp[x] = id ）。
建立双向指针关系：
pre[id] = p ：新节点的前驱指针指向位置 p 。
ne[id] = ne[p] ：新节点的后继指针指向 p  原本的后继节点。
更新原后继节点和位置 p  的指针：
pre[ne[p]] = id ： p  原后继节点的前驱指针指向新节点。
ne[p] = id ：位置 p  的后继指针指向新节点，完成插入。

2. 特性与意义

该操作的时间复杂度为 O(1)，仅需修改几个指针的指向即可完成插入，体现了静态双向链表高效插入的优势。
结合映射表 mp  实现了“元素值与存储位置的快速关联”，在需要频繁按值操作的场景中实用性很强。

2.6 在任意位置之前插⼊元素

// 在存储位置为 p 的元素前⾯，插⼊⼀个元素 x 1
void insert_front(int p, int x)
{id++;e[id] = x;mp[x] = id; // 存⼀下 x 这个元素的位置// 先左指针指向 p 的前驱，右指针指向 ppre[id] = pre[p];ne[id] = p;// 先让 p 的前驱的右指针指向 id// 再让 p 的左指针指向 idne[pre[p]] = id;pre[p] = id;
}
这是静态双向链表的“在任意位置之前插入元素”函数 insert_front ，用于在存储位置 p  之前插入元素 x 。
1. 函数逻辑

分配新节点： id++  为新元素 x  分配数组下标 id ，将 x  存入数据域数组 e[id] ，并通过映射表 mp  记录 x  的位置（ mp[x] = id ）。
建立双向指针关系：
pre[id] = pre[p] ：新节点的前驱指针指向 p  节点的前驱。
ne[id] = p ：新节点的后继指针指向位置 p 。
更新 p  前驱和 p  节点的指针：
ne[pre[p]] = id ： p  前驱节点的后继指针指向新节点。
pre[p] = id ： p  节点的前驱指针指向新节点，完成插入。

2. 特性与意义

时间复杂度为 O(1)，仅需修改几个指针的指向即可完成插入，利用双向链表的前驱指针 pre  实现了“在任意位置前高效插入”的能力。
结合映射表 mp  实现元素与位置的快速关联，在需要频繁按值操作的场景中实用性突出。

2.7 删除任意位置的元素

// 删除下标为 p 的元素
void erase(int p)
{mp[e[p]] = 0; // 从标记中移除ne[pre[p]] = ne[p];pre[ne[p]] = pre[p];
}
这是静态双向链表的“删除任意位置元素”函数 erase ，用于删除下标为 p  的元素。
1. 函数逻辑

从映射表中移除： mp[e[p]] = 0  将待删除元素从映射表中移除，避免后续误查。
修改双向指针关系：
ne[pre[p]] = ne[p] ：让 p  前驱节点的后继指针指向 p  的后继节点。
pre[ne[p]] = pre[p] ：让 p  后继节点的前驱指针指向 p  的前驱节点，从而跳过 p  节点完成逻辑删除。

2. 特性与意义

时间复杂度为 O(1)，仅需修改几个指针的指向即可完成删除，利用双向链表的前驱、后继指针实现了“常数时间”的高效删除。
该操作体现了静态双向链表在元素删除场景下的优势，无需遍历即可快速调整节点间的链接关系。

2.8 测试所有代码

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
// 创建双链表
int e[N], ne[N], pre[N], id, h;
int mp[N]; // mp[i] 表⽰：i 这个值存储的位置
// 遍历链表
void print()
{for (int i = ne[h]; i; i = ne[i]){cout << e[i] << " ";}cout << endl << endl;
}
// 头插
void push_front(int x)
{id++;e[id] = x;mp[x] = id;// 先修改新来结点的左右指针pre[id] = h;ne[id] = ne[h];// 修改哨兵位下⼀个结点的左指针pre[ne[h]] = id;ne[h] = id;
}
int find(int x)
{return mp[x];
}
// 在任意位置 p 的后⾯插⼊新的元素 x
void insert_back(int p, int x)
{id++;e[id] = x;mp[x] = id;pre[id] = p;ne[id] = ne[p];pre[ne[p]] = id;ne[p] = id;
}
// 在任意位置 p 的前⾯插⼊新的元素 x
void insert_front(int p, int x)
{id++;e[id] = x;mp[x] = id;pre[id] = pre[p];ne[id] = p;ne[pre[p]] = id;pre[p] = id;
}
// 删除任意位置 p 的元素
void erase(int p)
{mp[e[p]] = 0; // 把标记清空ne[pre[p]] = ne[p];pre[ne[p]] = pre[p];
}
int main()
{for (int i = 1; i <= 5; i++){push_front(i);print();}//cout << find(3) << endl;//cout << find(5) << endl;//cout << find(0) << endl;// insert_front(2, 22);// print();// insert_front(3, 33);// print();// insert_front(4, 44);// print();erase(2);print();erase(4);print();return 0;
}

4. 循环链表的模拟实现

回看之前实现的带头单向链表。我们定义表⽰空指针，但其实哨兵位就在位置，所有的结构正

好成环。因此循环链表就是在原有的基础上，让最后⼀个元素指向表头即可。

5. 总结:

本文系统介绍了静态链表的实现原理和操作，重点讲解了单链表和双向链表的静态数组实现方法。主要内容包括：1. 静态链表的核心组件：使用数组e[N]存储数据，ne[N]存储后继节点下标，通过下标id分配新节点位置；2. 单链表操作实现：详细说明了头插、遍历、按值查找、任意位置插入和删除等操作的O(1)实现方法；3. 双向链表扩展：在单链表基础上增加pre[N]数组实现前驱指针，支持双向遍历和前向插入操作；4. 性能优化技巧：引入mp数组实现O(1)时间复杂度的按值查找，体现空间换时间的优化思想；5. 实际应用建议：强调静态链表在算法竞赛中的高效性，同时分析了不适合实现尾操作的原因。文章通过清晰的代码示例和逻辑分析，展示了静态链表这一重要数据结构的高效实现方式。

查看全文

http://www.dtcms.com/a/390805.html