种群演化优化算法：原理与Python实现

种群演化优化算法是一类受自然进化过程启发的元启发式算法，其核心思想是通过模拟生物种群的遗传、变异、选择和自然淘汰等机制，在解空间中寻找最优解。这类算法不依赖于问题的梯度信息，对目标函数的性质要求很低，能够有效处理复杂的非线性、多峰和不可微的优化问题。

算法理论基础

基本数学原理

种群演化优化算法的数学基础可以表述为：

设优化问题为寻找目标函数 $f(x)$ 的最优值，其中 $x\in S$，$S$ 为搜索空间。算法维护一个包含 $N$ 个个体的种群 P={ x1,x2,...,xN}P = \{x_1, x_2, ..., x_N\}P={ x1​,x2​,...,xN​}。

适应度函数用于评估个体质量：
$$F(x_i)=\{\begin{array}{ll}f(x_i)& \text{对于最大化问题}\\ -f(x_i)& \text{对于最小化问题}\end{array}$$

选择概率基于适应度比例：
$$p_i=\frac{F(x_i)}{{\sum }_{j=1}^{N}F(x_j)}$$

二进制编码将连续变量离散化：
$$x=L+\frac{U-L}{2^L-1}\cdot \sum _{i=0}^{L-1}{b}_i\cdot 2^i$$
其中 $L$ 和 $U$ 为变量上下界，$b_i$ 为二进制位。

算法流程

1. 初始化：随机生成初始种群
2. 评估：计算每个个体的适应度
3. 选择：根据适应度选择优秀个体
4. 交叉：通过基因重组产生新个体
5. 变异：引入随机变化维持多样性
6. 终止判断：满足条件则停止，否则回到步骤2

差分进化算法

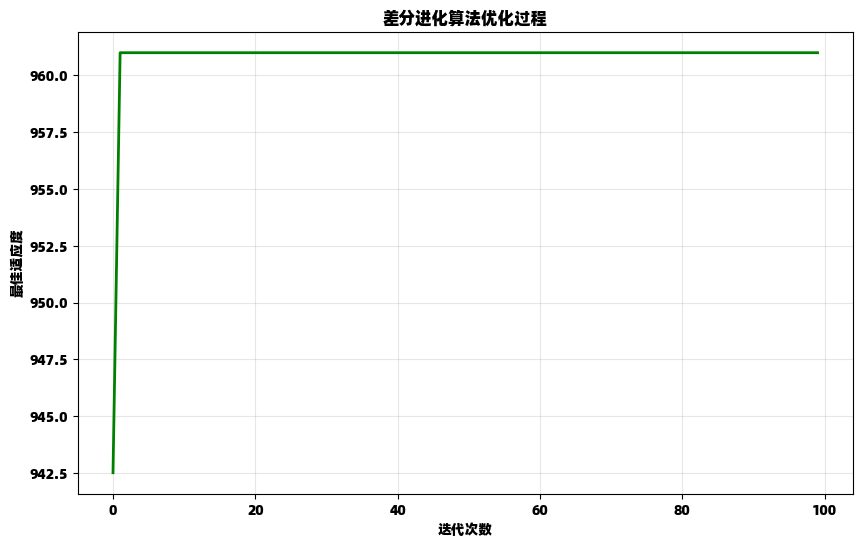
import numpy as np
import matplotlib.pyplot as plt# 修复后的差分进化算法实现
def run_differential_evolution():# 参数设置POP_SIZE = 30F = 0.5CR = 0.7N_GENERATIONS = 100BOUNDS = (0, 31)# 目标函数def objective_function(x):return x ** 2# 初始化种群def initialize_population():return np.random.uniform(BOUNDS[0], BOUNDS[1], POP_SIZE)# 变异操作def mutate(population, i):indexes = [idx for idx in range(POP_SIZE)