当前位置：首页 > news >正文

TPAMI 25 ICML 25 Oral | 顶刊顶会双认证！SparseTSF以稀疏性革新长期时序预测！

news 2025/9/20 6:19:14

本文介绍了一种新颖且极轻量级的长期时间序列预测（LTSF） 方法SparseTSF，旨在以最少计算资源应对长时域复杂时序依赖建模挑战。该方法核心是跨周期稀疏预测技术，通过对原始序列下采样，将预测任务简化为跨周期趋势预测，不仅大幅降低模型复杂度与参数数量，还作为隐式正则化机制提升模型鲁棒性，实现性能与效率的最优平衡。基于此技术，SparseTSF仅用不到1000个参数，便能取得与现有先进方法相当的性能，且泛化能力突出，适用于计算资源有限、样本量小或数据质量低的场景，本文已被TPAMI & ICML Oral两大顶刊顶会同时接收。

另外我整理了ICML 2025时间序列相关论文+源码，感兴趣的自取~
论文这里
在这里插入图片描述

2. 【论文基本信息】

论文信息

论文标题：SparseTSF: Lightweight and Robust Time Series Forecasting via Sparse Modeling
作者：Shengsheng Lin, Weiwei Lin (Senior Member, IEEE), Wentai Wu (Member, IEEE), Haojun Chen, and C. L. Philip Chen (Fellow, IEEE)
作者机构：华南理工大学，鹏城实验室，暨南大学
论文来源：TPAMI2025 & ICML2025 Oral
论文链接：https://ieeexplore.ieee.org/abstract/document/11141354
项目链接：https://github.com/lss-1138/SparseTSF

3.【背景及相关工作】

3.1 研究背景

时间序列预测的价值与挑战：时间序列预测在交通流量、产品销售、能源消耗等领域意义重大，能助力决策者提前规划，但精准预测常依赖复杂深度学习模型（如RNN、CNN、GNN、Transformer）。
长期时间序列预测（LTSF）的需求与难点：近年来LTSF需求增长，需模型提供长时域预测以支持进阶规划，但更长预测时域会带来更高不确定性，要求模型从更长历史窗口提取更广泛时序依赖，导致建模复杂度升高（如Transformer类模型参数达数百万至数千万），限制其在计算资源受限场景的应用。
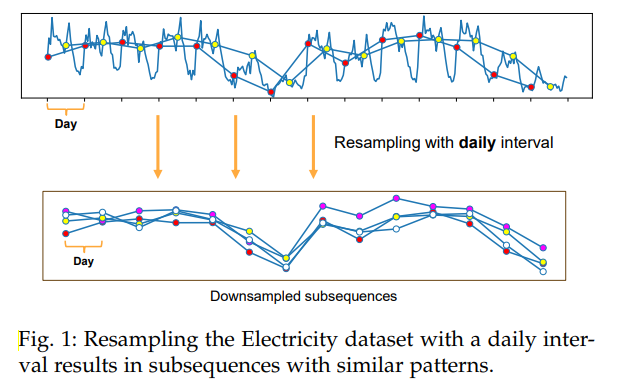
核心突破点：LTSF的准确性依赖数据内在周期性与趋势，通过对原始序列按周期重采样，可将周期模式转化为子序列间动态、趋势模式转化为子序列内特征，此分解为设计轻量级LTSF模型提供新视角，SparseTSF由此提出。

3.2 相关工作

3.2.1 长期时间序列预测（LTSF）领域发展

Transformer类模型主导初期：Transformer因强长期依赖建模能力受关注，LogTrans、TFT、Informer、Autoformer等模型通过修改原始结构适配LTSF；近年PatchTST、Crossformer等则证明，结合计算机视觉领域的patch策略，原始Transformer架构也能实现出色效果。
多类型模型并行发展：除Transformer外，CNN（如SCINet、TimesNet）、MLP（如NHITS、TimeMixer）类方法是主流；预训练大语言模型（LLM）迁移至时序领域、RNN（如SegRNN）与GNN（如FourierGNN）网络也能在LTSF任务中表现良好，但这些模型普遍参数量大，限制实际应用。

3.2.2 轻量级预测模型进展

轻量化探索起步：自DLinear证明简单模型可提取强时序周期依赖后，LightTS、TiDE、TSMixer等研究推动LTSF模型向轻量化发展。
关键里程碑与突破：FITS是轻量化LTSF的里程碑，首次将模型参数降至1万级并保持优性能，其通过将时域预测任务转化为频域任务、用低通滤波器减少参数实现；而本文提出的SparseTSF进一步突破，借助跨周期稀疏预测技术，首次将LTSF模型参数降至1千以下，推动轻量化发展至新高度。

4.【研究方法论】

4.1 预备知识（Preliminaries）

4.1.1 长期时间序列预测（LTSF）定义

任务目标：利用历史多变量时间序列（MTS）数据预测长时域未来值，公式定义为 $yˉt+1:t+H=fθ(xt−L+1:t)\bar{y}_{t+1: t+H}=f_{\theta}(x_{t-L+1: t})$ ，其中 $xt−L+1:t∈RL×Cx_{t-L+1: t} \in \mathbb{R}^{L ×C}$ 表示长度为 $L$ （历史回溯窗口长度）、通道数为 $C$ （特征数量）的历史数据， $yˉt+1:t+H∈RH×C\bar{y}_{t+1: t+H} \in \mathbb{R}^{H ×C}$ 表示长度为 $H$ （预测时域长度）的预测结果。
核心挑战：实际应用中需延长预测时域 $H$ 以提供更丰富指导，但 $H$ 延长会增加模型复杂度，导致主流模型参数激增，因此需研发轻量且鲁棒的模型。

4.1.2 通道独立策略（Channel-Independent Strategy）

核心思路：针对多变量时间序列，聚焦单个单变量序列进行预测，而非利用全部多变量历史数据。为每个单变量序列寻找共享函数 $fθ:xt−L+1:t(i)∈RL→yˉt+1:t+H(i)∈RHf_{\theta}: x_{t-L+1: t}^{(i)} \in \mathbb{R}^{L} \to \bar{y}_{t+1: t+H}^{(i)} \in \mathbb{R}^{H}$ ，减少对通道间关系建模的复杂度。
应用逻辑：当前主流模型目标已转向建模单变量序列的长期依赖（周期性、趋势），本文同样采用该策略，后续公式省略通道维度，默认输入 $\in \mathbb{R}^{L}$ 、输出 $yˉ∈RH\bar{y} \in \mathbb{R}^{H}$ 。

4.2 SparseTSF模型设计

Overall Pseudocode of SparseTSF

4.2.1 跨周期稀疏预测技术（Cross-Period Sparse Forecasting）

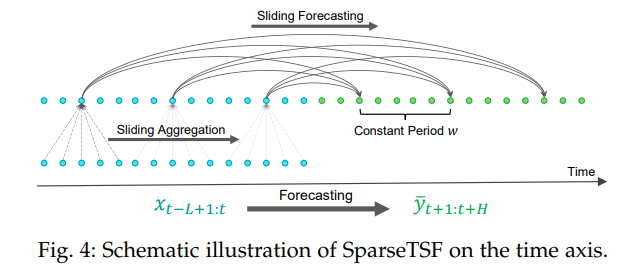
核心流程：基于数据的固定周期性（如电力消耗、交通流量的日周期），通过“下采样-预测-上采样”实现预测，具体步骤如下：
1. 下采样（Downsampling）：假设时间序列 $x$ 周期为 $w$ ，将原始序列下采样为 $w$ 个子序列，每个子序列长度 $n=⌊Lw⌋n=\left\lfloor\frac{L}{w}\right\rfloor$ ，数学表达为 $X_{i, k}=x_{i+k × w}$ （ $i = 1, 2, ..., w$ ； $k = 1, 2, ..., n$ ），可通过将 $x$ 重塑为 $n \times w$ 矩阵后转置为 $w \times n$ 矩阵 $X$ 实现。
2. 子序列预测：采用参数共享的骨干模型 $fθf_{\theta}$ 对每个下采样子序列预测，得到 $w$ 个长度为 $m=⌊Hw⌋m=\left\lfloor\frac{H}{w}\right\rfloor$ 的预测子序列，公式为 $Y‾i=fθ(Xi)\overline{Y}_{i}=f_{\theta}\left(X_{i}\right)$ （ $i = 1, 2, ..., w$ ）。
3. 上采样（Upsampling）：将预测子序列重组为完整预测序列，数学表达为 $y‾i+l×w=Y‾i,l\overline{y}_{i+l × w}=\overline{Y}_{i, l}$ （ $i = 1, 2, ..., w$ ； $l = 1, 2, ..., m$ ），可通过将 $w \times m$ 矩阵 $Yˉ\bar{Y}$ 转置后重塑为长度 $H$ 的序列 $yˉ\bar{y}$ 实现。
优化改进（滑动聚合）：为解决下采样可能导致的信息丢失与异常值影响，在稀疏预测前对原始序列执行滑动聚合，通过1D卷积（零填充，核大小 $×\left\lfloor\frac{w}{2}\right\rfloor+1$ ）实现，公式为 $x^{'} = x + C o n v 1 D (x)$ ，聚合后的数据点包含周期内邻域信息，同时通过加权平均减轻异常值影响。

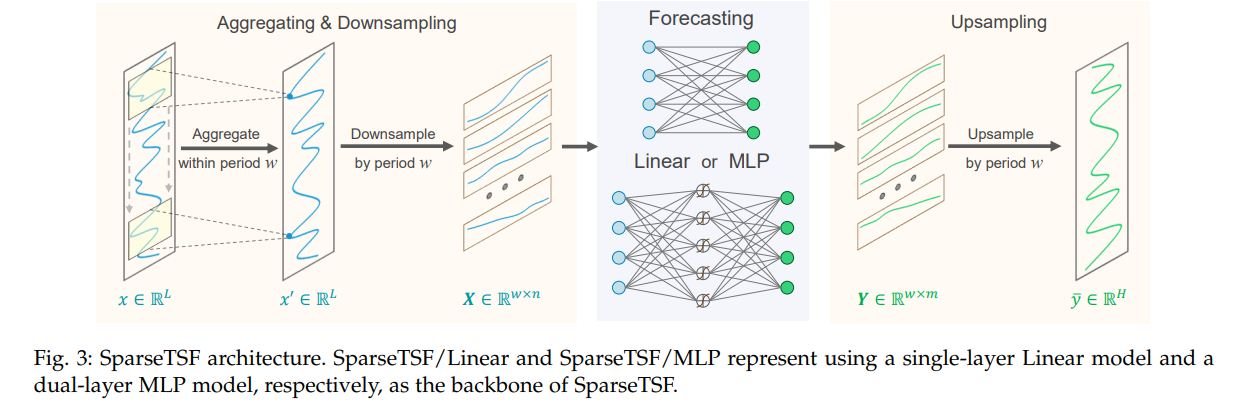
4.2.2 骨干模型（Backbone）

模型选型：为极致轻量化，采用两种简单骨干模型构建SparseTSF变体：
1. SparseTSF/Linear：单一层线性模型，结构最简单，参数最少。
2. SparseTSF/MLP：双层MLP模型，以ReLU为激活函数，具备更强非线性学习能力，更适用于高维多变量预测场景（可捕捉多通道不同模式）。

4.2.3 实例归一化（Instance Normalization）

作用：缓解训练与测试数据集间的分布偏移，提升模型鲁棒性。
操作步骤：输入模型前，将序列减去自身均值 $μ\mu$ ，公式为 $x=x−μx=x-\mu$ ；模型输出后，将均值加回预测结果，公式为 $y‾=y‾+μ\overline{y}=\overline{y}+\mu$ 。

4.2.4 损失函数（Loss Function）

选型：采用主流的均方误差（MSE）作为损失函数，衡量预测值与真实值的差异。
公式： $Loss=∥y−y‾∥22\mathcal{L}oss=\| y-\overline{y}\| _{2}^{2}$ ，其中 $y$ 为真实值， $yˉ\bar{y}$ 为预测值。

4.3 理论分析（Theoretical Analysis）

4.3.1 参数效率（Parameter Efficiency）

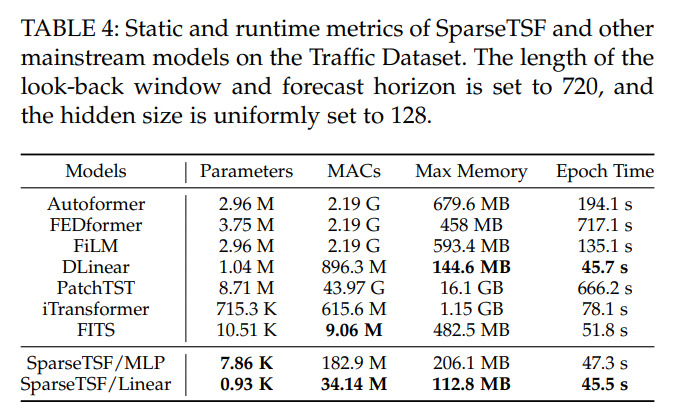
定理4.1（参数数量）：给定历史回溯窗口长度 $L$ 、预测时域 $H$ 与周期 $w$ ，SparseTSF总参数数量为 $⌊Lw⌋×⌊Hw⌋+2×⌊w2⌋+1\left\lfloor\frac{L}{w}\right\rfloor \times\left\lfloor\frac{H}{w}\right\rfloor+2 \times\left\lfloor\frac{w}{2}\right\rfloor+1$ 。
证明过程：
1. 模型含两个核心组件：滑动聚合用1D卷积层（无偏置）与稀疏滑动预测用线性层（无偏置）。
2. 1D卷积层参数数量由核大小决定，为 $×\left\lfloor\frac{w}{2}\right\rfloor+1$ ；线性层参数数量为 $n \times m$ （ $n=⌊Lw⌋n=\left\lfloor\frac{L}{w}\right\rfloor$ ， $m=⌊Hw⌋m=\left\lfloor\frac{H}{w}\right\rfloor$ ）。
3. 总参数为两部分之和，即 $⌊Lw⌋×⌊Hw⌋+2×⌊w2⌋+1\left\lfloor\frac{L}{w}\right\rfloor \times\left\lfloor\frac{H}{w}\right\rfloor+2 \times\left\lfloor\frac{w}{2}\right\rfloor+1$ 。
实例验证：当 $L = 720$ 、 $H = 720$ 、 $w = 24$ 时，参数数量为 $925$ ，远小于标准线性模型的 $L \times H = 518400$ ，证明其轻量性。

4.3.2 隐式正则化（Implicit Regularization）

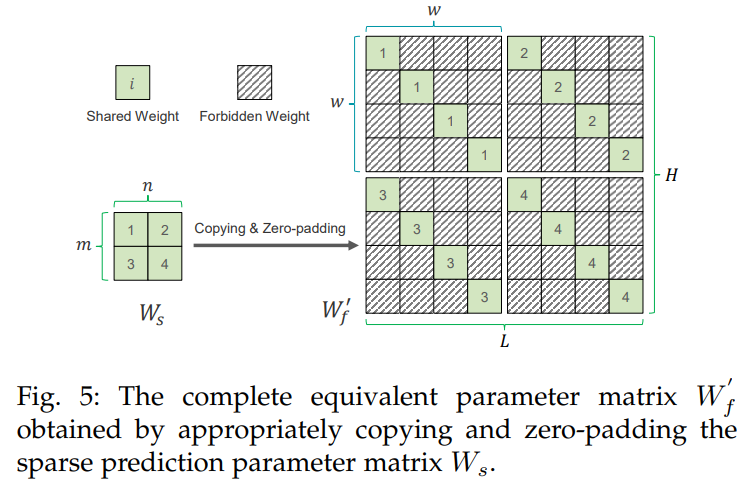
定理4.2（SparseTSF/Linear模型优化目标）：结合稀疏技术的线性模型优化目标为 $_{W_{f}}\left\| y-W_{f} x\right\| _{2}^{2}+\alpha\left\| W_{forbid }\right\| _{1}+\beta\left\| \sigma^{2}\left(W_{shared }\right)\right\| _{1}$ ，其中 $α,β→∞\alpha, \beta \to \infty$ ，且：
1. $∥Wforbid∥1=∑k=1m∑l=1n∑i≠j∣(Wf)i+kw,j+lw∣\left\| W_{forbid }\right\| _{1}=\sum_{k=1}^{m} \sum_{l=1}^{n} \sum_{i \neq j}\left|\left(W_{f}\right)_{i+k w, j+l w}\right|$ ：惩罚 $W_f$ 中 $w \times w$ 子矩阵的非对角元素，驱动其趋近于0，形成块稀疏结构。
2. $∥σ2(Wshared)∥1=∑k=1m∑l=1n∣σ2((Wf)i+kw,j+lw⏟i=j)∣\left\| \sigma^{2}\left(W_{shared }\right)\right\| _{1}=\sum_{k=1}^{m} \sum_{l=1}^{n}\left|\sigma^{2}(\underbrace{\left(W_{f}\right)_{i+k w, j+l w}}_{i=j})\right|$ ：约束 $w \times w$ 子矩阵对角元素的方差，迫使对角元素相等，实现参数共享。
核心结论：稀疏预测技术相当于隐式 $ℓ1\ell_1$ 正则化，可增强模型对噪声的鲁棒性与泛化能力，其结构化稀疏设计能让模型更精准提取数据中有意义的特征，在极端压缩参数的同时提升预测性能。

5.【实验结果】

5.1 实验设置

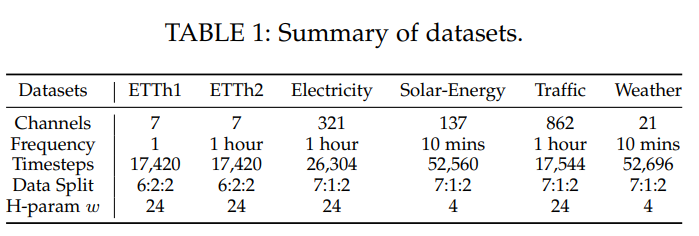
数据集：6个主流LTSF数据集（ETTh1/2、Electricity等），含不同周期，超参数(w)按周期设（如日周期(w=24)），数据划分6:2:2或7:1:2。
基线与环境：对比Autoformer、DLinear等主流模型，修复测试数据bug，统一(L=720)；PyTorch实现，Adam优化，30轮训练，RTX 4090 GPU运行。

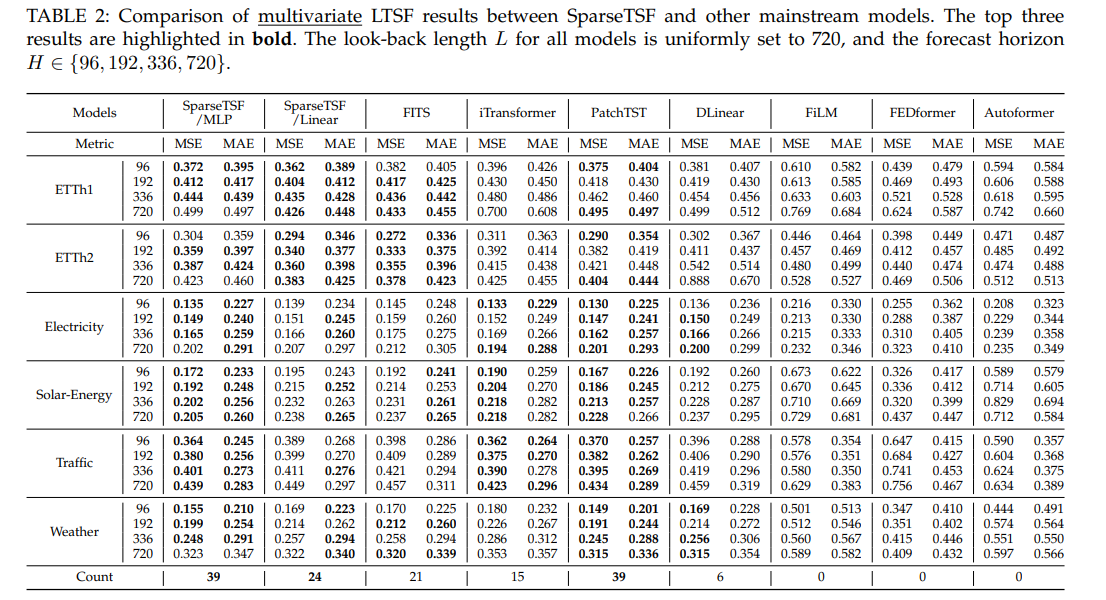
5.2 核心预测性能

多变量预测：SparseTSF（Linear/MLP）多数场景前三，MLP变体39次前三（优于Linear的24次），适配高维数据。
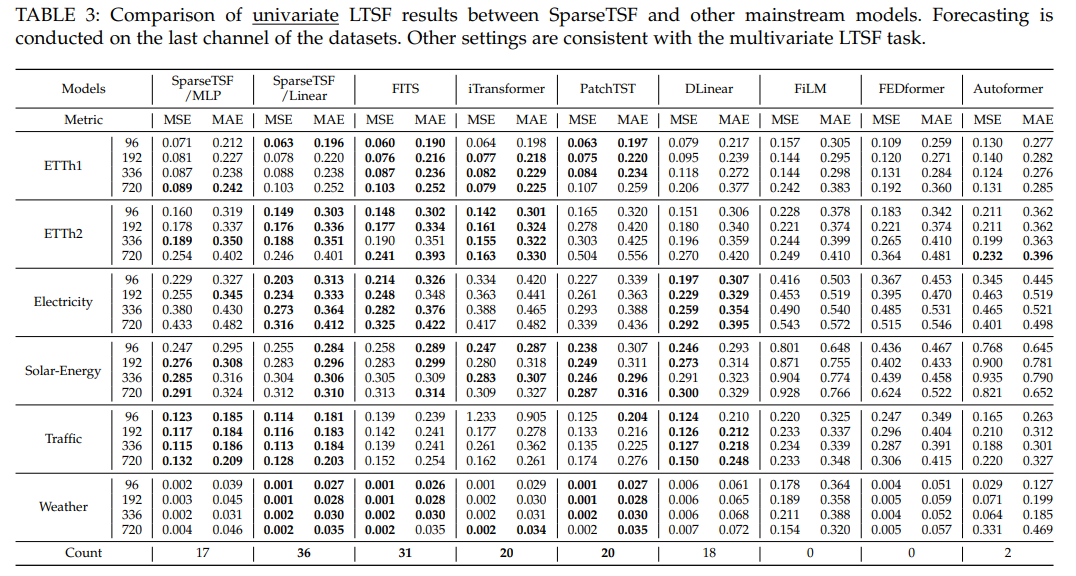
单变量预测：SparseTSF/Linear达最优，线性模型（如FITS）表现优于深度非线性模型（如PatchTST）。

5.3 效率优势

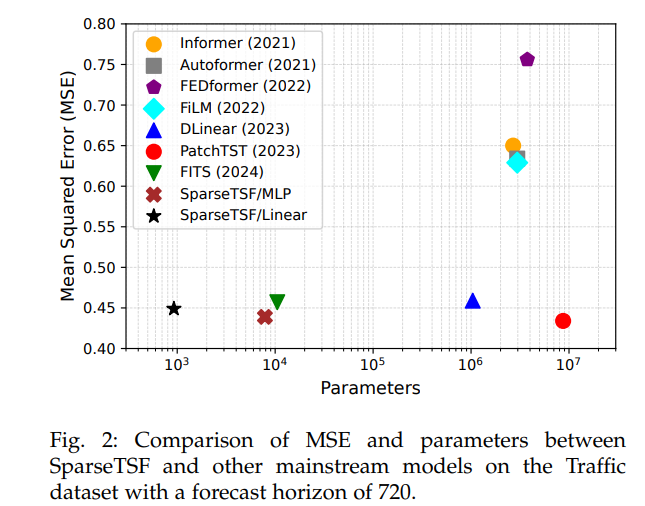
Comparison of MSE and parameters between SparseTSF and other mainstream models on the Traffic dataset with a forecast horizon of 720

参数：Linear变体<1000，MLP变体<8000，远低于FITS（10k级）及其他基线（如DLinear 1.04M）。
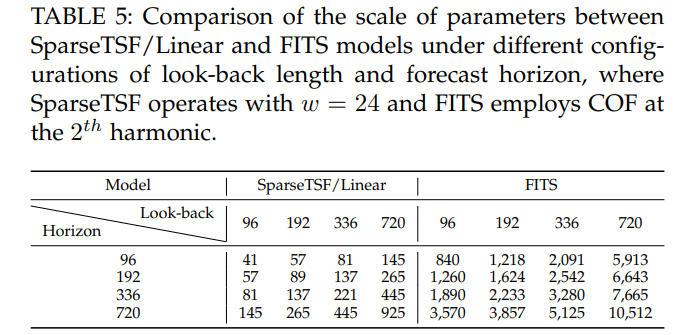
runtime：Traffic数据集上，Linear变体内存112.8MB、单轮45.5s，优于FITS（482.5MB、51.8s）及PatchTST（16.1GB、666.2s）。

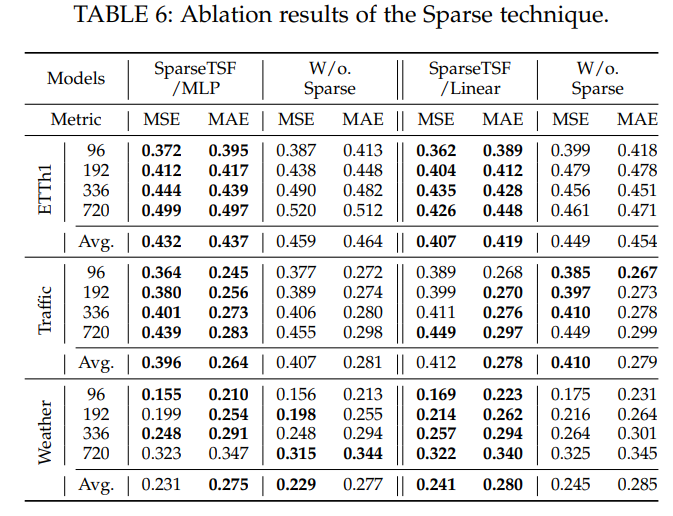
5.4 关键分析

稀疏技术有效性：ETTh1等数据集多数情况降误差，验证技术价值。
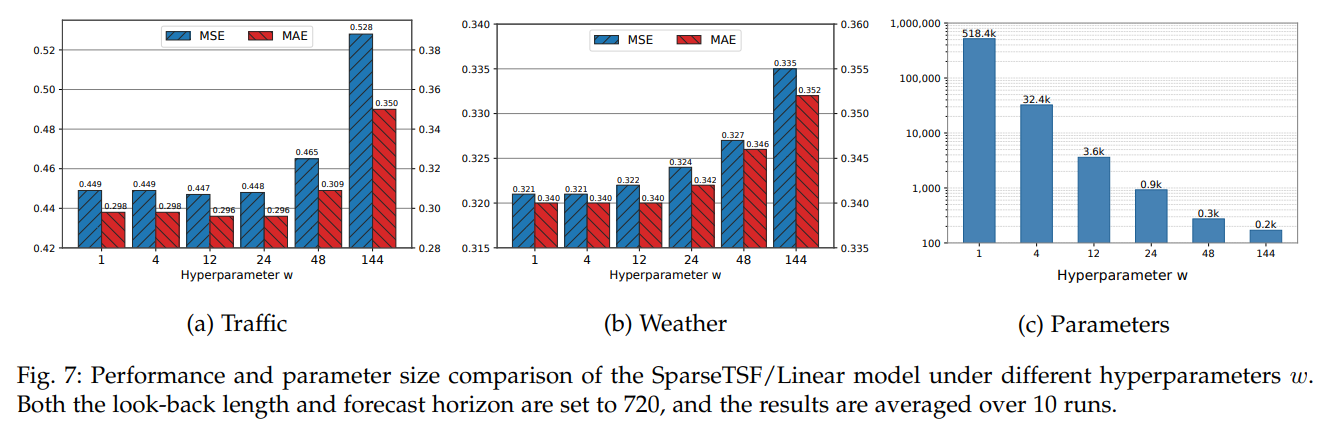
超参数(w)：匹配周期（如(w=24)）性能最优，长周期数据调小(w)平衡精度与参数。
泛化能力：同周期跨域（如ETTh2→ETTh1）表现佳，周期不匹配仍保鲁棒性。
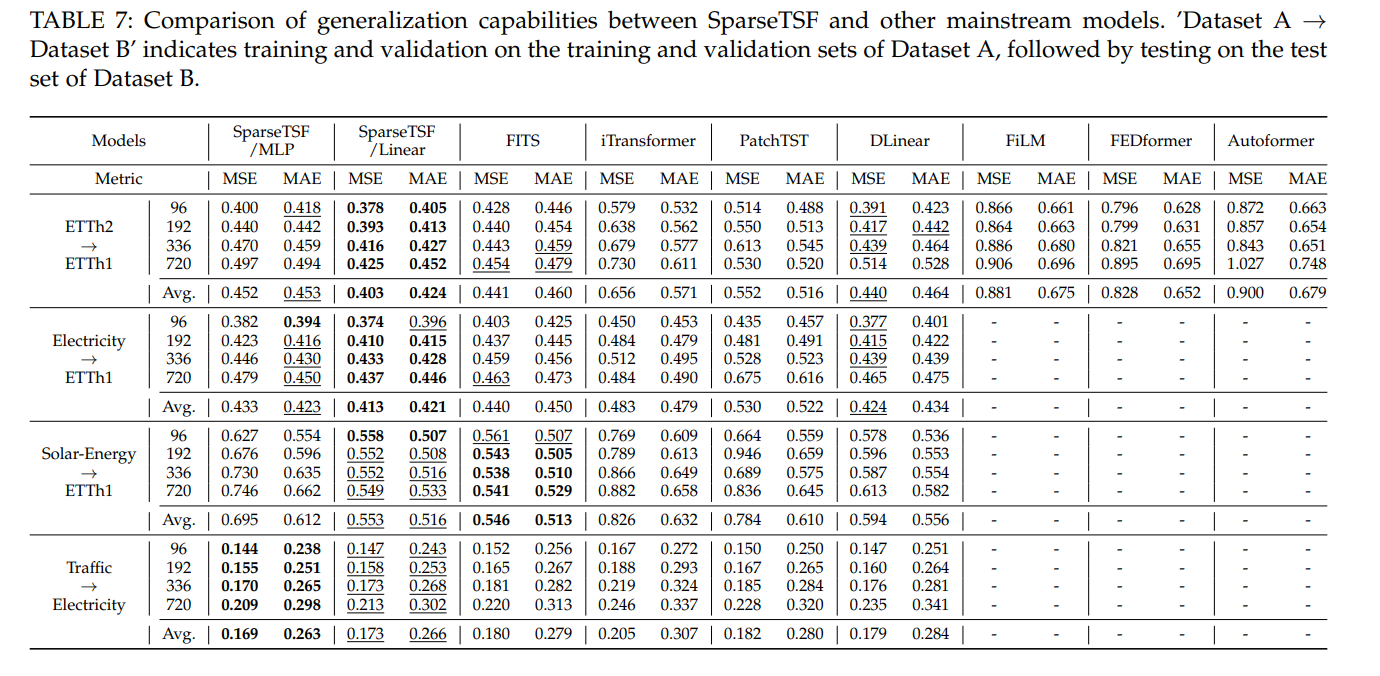
回溯窗口(L)：需覆盖完整周期（如含周周期需(L≥168)），长窗口提升性能。
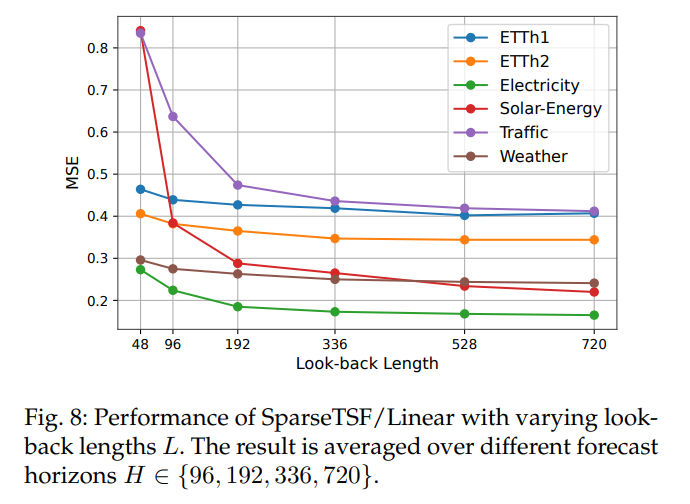
CI策略：长(L)（如720）下，CI方法优于CD方法，MLP变体适配多通道复杂场景。

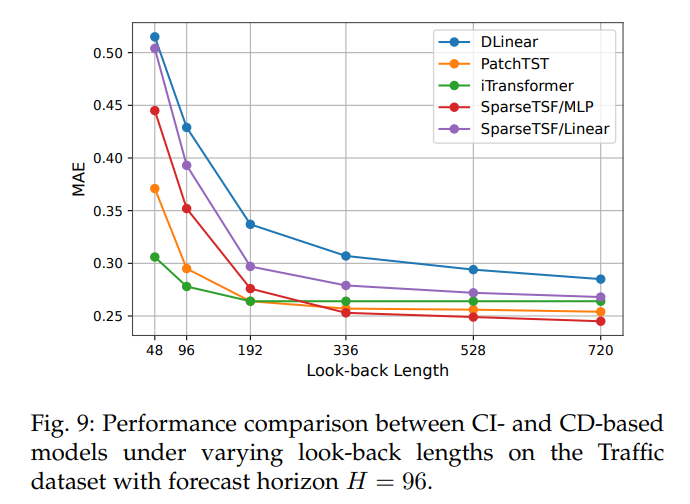
6.【总结展望】

6.1 总结

本文提出跨周期稀疏预测技术及对应的SparseTSF模型，以解决长期时间序列预测（LTSF）中模型复杂、参数冗余的问题。该技术通过对原始序列按周期下采样，将预测任务简化为跨周期趋势预测，既实现数据周期性与趋势的有效解耦，又极大压缩模型参数（Linear变体<1000参数，MLP变体<8000参数）；理论分析证明其稀疏技术可作为隐式正则化，增强模型鲁棒性与泛化能力。实验验证显示，SparseTSF在多变量/单变量LTSF任务中均达竞争性能（如多变量任务MLP变体获39次前三），且效率远超FITS、DLinear等基线，适配计算资源受限、小样本或低质量数据场景，为轻量级LTSF模型发展提供重要突破。

6.2 展望

当前SparseTSF在超长期周期数据（如周期>100）、多交织周期数据（如日-周周期叠加）及回溯窗口不足场景中存在局限，未来将通过设计额外信息提取模块突破这些限制，例如针对多周期数据开发多尺度下采样机制，针对超长期周期数据优化参数连接密度。同时，将进一步探索模型在更复杂时序场景（如含强噪声、非平稳数据）的适配性，持续追求性能与参数规模的最优平衡，推动轻量级LTSF模型在更多实际领域的应用。

7.【即插即用模块代码】

7.1 时间序列分解模块（series_decomp）

功能：将时间序列分解为季节性成分和趋势成分，以便模型分别对不同成分进行处理和预测，提升时间序列预测性能。
核心代码段（即插即用关键）：

class series_decomp(nn.Module):"""Series decomposition block"""def __init__(self, kernel_size):super(series_decomp, self).__init__()self.moving_avg = moving_avg(kernel_size, stride=1)def forward(self, x):moving_mean = self.moving_avg(x)res = x - moving_meanreturn res, moving_mean

即插即用优势：该模块结构独立，仅需传入合适的核大小即可初始化。可轻松嵌入到各种时间序列预测模型（如DLinear、Autoformer、FEDformer、PatchTST等）中，无需对模型主体结构进行大规模修改，能快速实现时间序列的分解功能，帮助模型捕捉不同特征成分。

7.2 多内核时间序列分解模块（series_decomp_multi）

功能：支持使用多个不同的核大小对时间序列进行分解，更灵活地处理具有复杂季节性和趋势特征的时间序列数据。
核心代码段（即插即用关键）：

# 从相关模型（如Film、Autoformer）中可推断其使用方式，结合series_decomp实现多内核分解
# 初始化方式示例
kernel_size = [25, 12]  # 多个核大小
self.decomp = series_decomp_multi(kernel_size)

即插即用优势：继承了series_decomp模块的即插即用特性，同时通过支持多内核大小，能适应更多样化的时间序列数据特征。可根据不同的数据特点灵活选择核大小组合，无需修改模块内部结构，直接在模型中替换单内核分解模块即可使用。

7.3 线性预测模块（Linear）

功能：通过简单的线性变换实现时间序列预测，作为基础预测模块，可单独使用或与其他复杂模块结合使用。
核心代码段（即插即用关键）：

class Model(nn.Module):"""Just one Linear layer"""def __init__(self, configs):super(Model, self).__init__()self.seq_len = configs.seq_lenself.pred_len = configs.pred_lenself.Linear = nn.Linear(self.seq_len, self.pred_len)# 可可视化权重的设置self.Linear.weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))def forward(self, x):# x: [Batch, Input length, Channel]x = self.Linear(x.permute(0,2,1)).permute(0,2,1)return x  # [Batch, Output length, Channel]

即插即用优势：结构简单，参数少，计算效率高。仅需配置序列长度和预测长度即可初始化，可快速集成到各种预测框架中作为基准模型或辅助预测模块，无需复杂的适配工作。

7.4 分解线性预测模块（DLinear中的分解与线性结合部分）

功能：先对时间序列进行分解，再分别对季节性成分和趋势成分应用线性预测，最后将结果融合，结合了分解模块和线性模块的优势。
核心代码段（即插即用关键）：

class Model(nn.Module):"""Decomposition-Linear"""def __init__(self, configs):super(Model, self).__init__()self.seq_len = configs.seq_lenself.pred_len = configs.pred_len# 分解核大小kernel_size = 25self.decompsition = series_decomp(kernel_size)self.Linear_Seasonal = nn.Linear(self.seq_len,self.pred_len)self.Linear_Trend = nn.Linear(self.seq_len,self.pred_len)def forward(self, x):# x: [Batch, Input length, Channel]seasonal_init, trend_init = self.decompsition(x)seasonal_init, trend_init = seasonal_init.permute(0, 2, 1), trend_init.permute(0, 2, 1)seasonal_output = self.Linear_Seasonal(seasonal_init)trend_output = self.Linear_Trend(trend_init)x = seasonal_output + trend_outputreturn x.permute(0, 2, 1)  # [Batch, Output length, Channel]