数据结构9——树

前言：
本专栏属于数据结构相关内容，附带一些代码加深对一些内容的理解，为方便读者观看，本专栏内的所有文章会同时附带C语言和Python对应的代码，（可自行通过目录跳转到对应的部分）辅助不同主修语言的读者去更好的理解对应的内容，若是代码0基础的读者，可先去博主其他专栏学习一下基础的语法及知识点：

魔法天才的跳转链接：

C语言：C基础_Gu_shiwww的博客-CSDN博客
Python语言：python1_Gu_shiwww的博客-CSDN博客
其他数据结构内容可见：数据结构_Gu_shiwww的博客-CSDN博客

1. 什么是树

树(Tree)是n(n>=0)个节点的有限集合T，它满足两个条件 ：

有且仅有一个特定的称为根（Root）的节点；
其余的节点可以分为m（m≥0）个互不相交的有限集合T1、T2、……、Tm，
其中每一个集合又是一棵树，并称为其根的子树（Subtree）。

特征：

一对多，每个节点最多有一个前驱，但可以有多个后继（根节点无前驱，叶节点无后继）

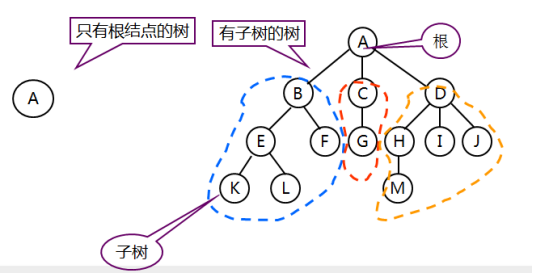
1.1 关于树的一些基本概念

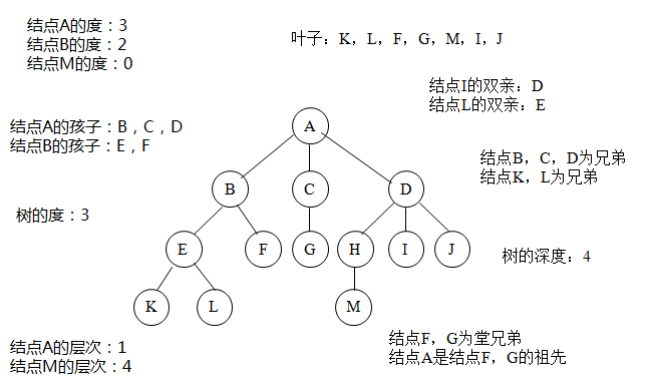
(1)度数：一个节点的子树的个数(一个节点的子树的个数称为该节点的度数,3)

(2)树度数：树中节点的最大度数

(3)叶节点或终端节点: 度数为零的节点

(4)分支节点：度数不为零的节点(B一层)

(5)内部节点：除根节点以外的分支节点 （B，C，D）

(6)节点层次: 根节点的层次为1，根节点子树的根为第2层，以此类推

(7)树的深度或高度: 树中所有节点层次的最大值

1.2 二叉树

1.2.1 概念

二叉树（Binary Tree）是n（n≥0）个节点的有限集合，它或者是空集（n＝0），

或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。
二叉树与普通有序树不同，二叉树严格区分左孩子和右孩子，即使只有一个子节点也要区分左右。//二叉树：节点最大的度数2
满二叉树和完全二叉树

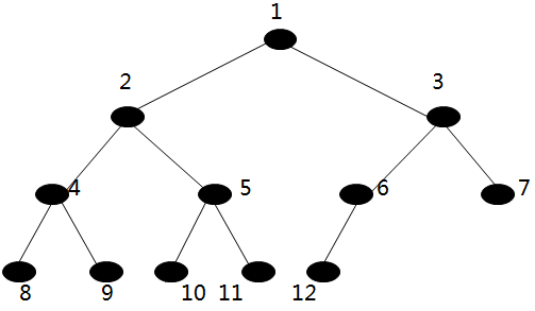
(1)满二叉树： 深度为k（k>=1）时节点为2k - 1(2的k次幂-1)

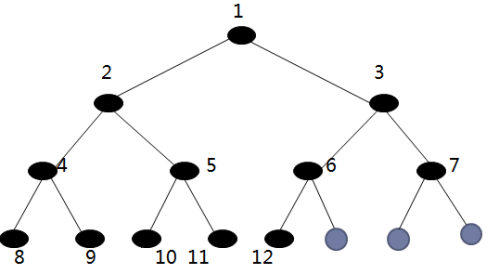
        完全二叉树:只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上

1.2.2 性质（重点）

1. 二叉树第k层（k>=1），节点最多是2的k-1次方个
2. 深度为k（k>=1）的二叉树最多有2的k次方-1个
3. 任意一棵二叉树，树叶的数目比度数为2的节点数目多1

总节点 = 各类节点的和 n = n0 + n1 + n2

总节点 = 所有子节点 + 根节点 n = n1 + 2n2 + 1

n0 + n1 + n2 = n1 + 2n2 + 1

n0 = n2 + 1

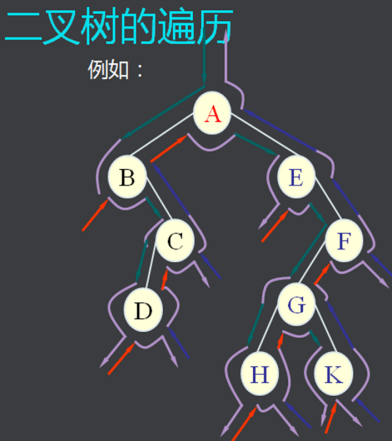
1.2.3 二叉树的遍历（重要）

前序：根 左 右
中序：左 根 右
后序：左 右 根

先序：

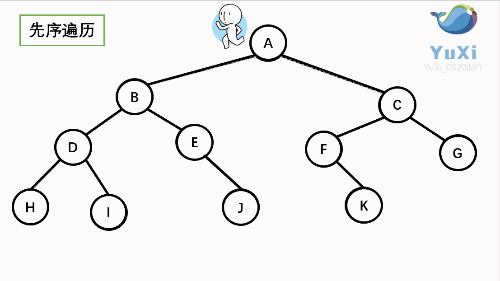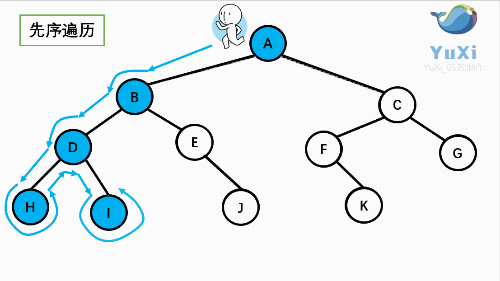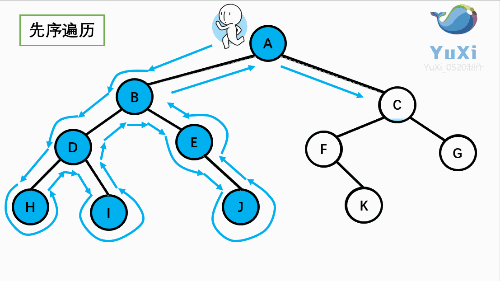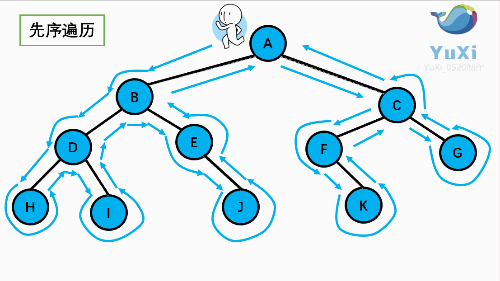
先序：根----->左----->右

ABDHIEJCFKG

中序：

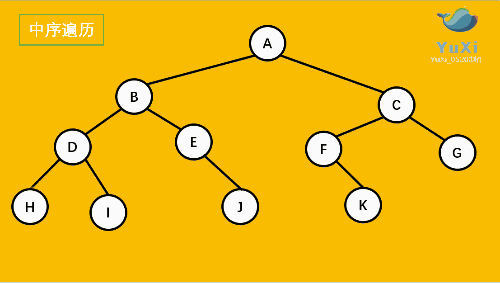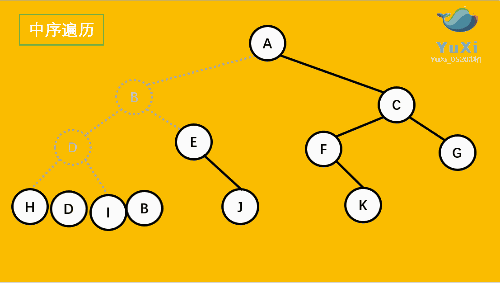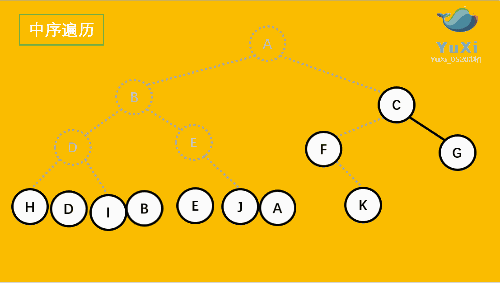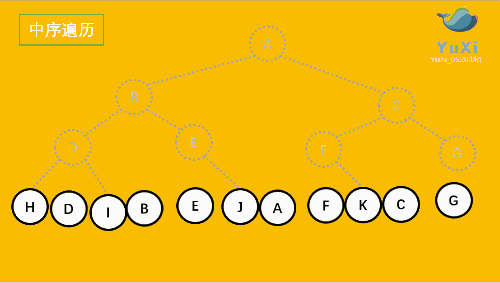
中序：左----->根----->右

HDIBEJAFKCG

后序：

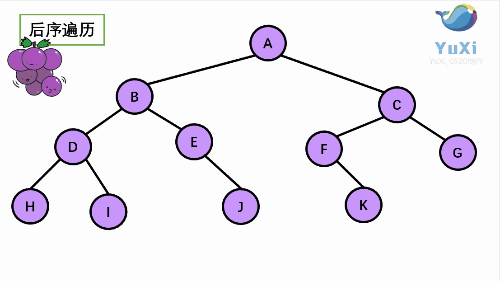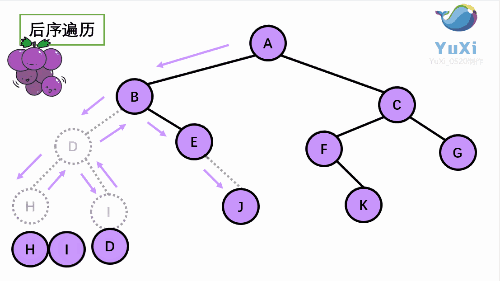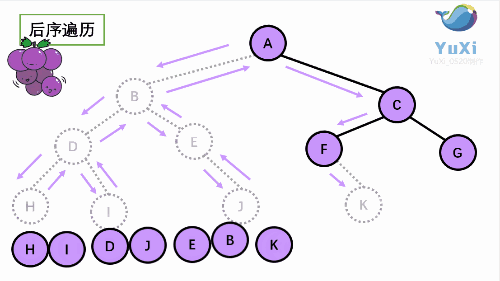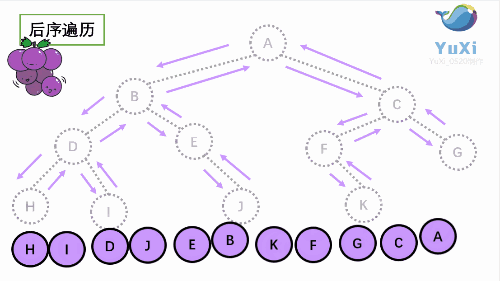
后序：左----->右----->根

HIDJEBKFGCA

*******练习*******

对应下图三种遍历方式输出的结果为：

前序：ABCDEFGHK
中序：BDCAEHGKF
后序：DCBHKGFEA

1.2.4 通过遍历结果画出二叉树

已知遍历结果如下，试着画出对应的二叉树

前序： A B C E H F I J D G K
中序： A H E C I F J B D K G

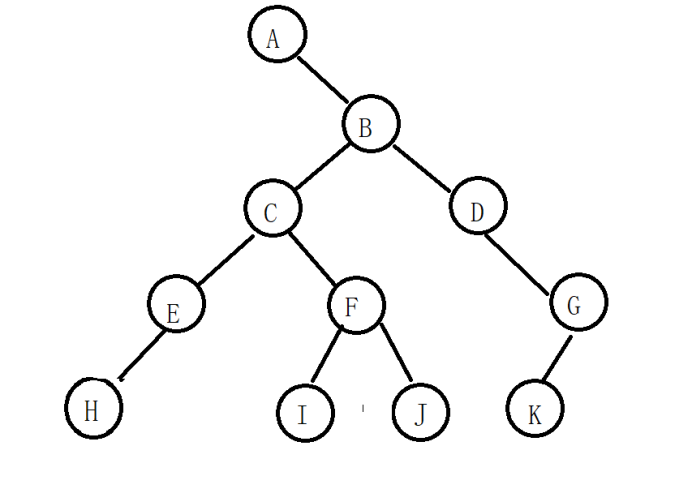
注意：

想要画出完整的树结构，必须要知道中序遍历。

1.2.5 存储结构

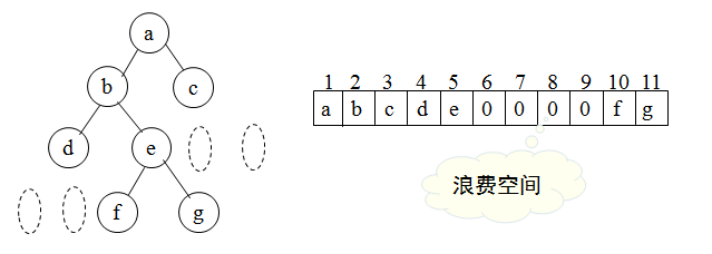
1）顺序存储

顺序存储结构 ：完全二叉树节点的编号方法是从上到下，从左到右，根节点为1号节点。

设完全二叉树的节点数为n
某节点编号为i
当i>1（不是根节点）时，有父节点，其编号为i/2;
当2*i<=n时，有左孩子，其编号为2*i ,否则没有左孩子，本身是叶节点;
当2*i+1<=n时，有右孩子，其编号为2*i+1 ,否则没有右孩子；

节点编号

根节点编号 1
根节点左子节点编号： 2 即 2 * 1
根节点右子节点编号： 3 即 2 * 1 + 1
第n个节点
左子节点编号： 2 * n
右子节点编号： 2 * n + 1
有n个节点的完全二叉树可以用有n+1 个元素的数组进行顺序存储，节点号和数组下标一一对应，下标为零的元素不用。

2）链式存储

当i>1（不是根节点）时，有父节点，其编号为i/2;
当2*i<=n时，有左孩子，其编号为2*i ,否则没有左孩子，本身是叶节点;
当2*i+1<=n时，有右孩子，其编号为2*i+1 ,否则没有右孩子

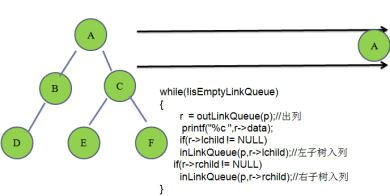
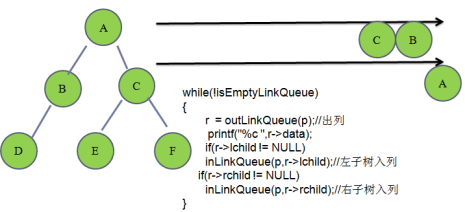
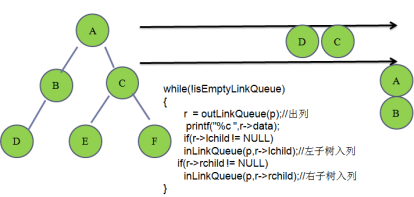
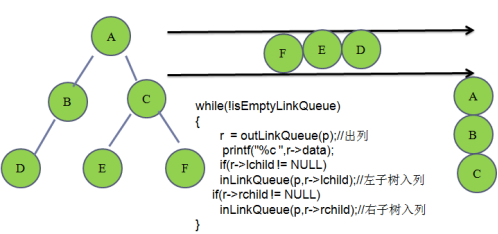
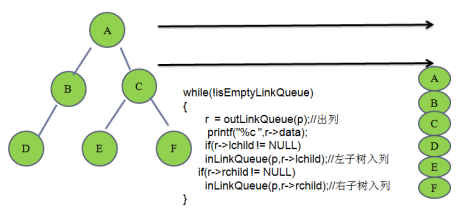
1.3 二叉树的层次遍历

2. 代码实现树的先序、中序、后序遍历

2.1 C语言编程实现三种遍历

#include <stdio.h>
#include <stdlib.h>typedef char datatype_tree;
typedef struct tree_node_t
{datatype_tree data;         // 数据域struct tree_node_t *lchild; // 左子leftstruct tree_node_t *rchild; // 右子right
} bitree_node_t, *bitree_list_t;
// 1.创建一棵树
bitree_list_t CreateBitree(int n, int i)
{bitree_list_t r = (bitree_list_t)malloc(sizeof(bitree_node_t));if (r == NULL){perror(" r malloc err");return NULL;}r->data = i;if (2 * i <= n) // 有左孩子r->lchild = CreateBitree(n, 2 * i);elser->lchild = NULL;if (2 * i + 1 <= n) // 有右孩子r->rchild = CreateBitree(n, 2 * i + 1);elser->rchild = NULL;return r;
}// 2.遍历前序
void PreOrder(bitree_list_t r)
{printf("%d  ", r->data); // 根if (r->lchild != NULL) // 左PreOrder(r->lchild);if (r->rchild != NULL) // 右PreOrder(r->rchild);
}
// 中序
void InOrder(bitree_list_t r)
{if (r->lchild != NULL) // 左InOrder(r->lchild);printf("%d  ", r->data); // 根if (r->rchild != NULL) // 右InOrder(r->rchild);
}
// 后序
void PostOrder(bitree_list_t r)
{if (r->lchild != NULL) // 左PostOrder(r->lchild);if (r->rchild != NULL) // 右PostOrder(r->rchild);printf("%d  ", r->data); // 根
}
// 层次遍历
void unOrder(bitree_list_t *r);// 释放
void Delete(bitree_list_t r)
{if (r->lchild != NULL)Delete(r->lchild);if (r->rchild != NULL)Delete(r->rchild);free(r);r = NULL;
}
int main(int argc, char const *argv[])
{bitree_list_t r = CreateBitree(5, 1);printf("前序遍历:");PreOrder(r);printf("\n中序遍历:");InOrder(r);printf("\n后序遍历:");PostOrder(r);printf("\n");Delete(r);r = NULL;return 0;
}

2.2 C语言编程实现层次遍历

//层次遍历
void unOrder(bitree_t *r)
{//1.创建一个队列,队列的数据域变成指向树节点的指针linkqueue_t *p = createEmptyLinkQueue();if(r != NULL)inLinkQueue(p,r);//2.循环打印while(!isEmptyLinkQueue(p)){r = outLinkQueue(p);printf("%c ",r->data);if(r->lchild != NULL)//只要左子不为空，就入列，之后出列的时候打印inLinkQueue(p,r->lchild);if(r->rchild != NULL)//只要右子不为空，就入列，之后出列的时候打印inLinkQueue(p,r->rchild);}
}

2.3 Python语言实现三种遍历方式

2.3.1 函数接口

class TreeNode:def __init__(self, data=None, left=None, right=None):self.data = dataself.left = leftself.right = rightdef create_bitree(n, i):passdef pre_order(r):passdef in_order(r):passdef post_order(r):pass

2.3.2 创建二叉树

def create_bitree(n, i):  # n = 3root = TreeNode(i)if 2 * i <= n:root.left = create_bitree(n, 2 * i)else:root.left = Noneif 2 * i + 1 <= n:root.right = create_bitree(n, 2 * i + 1)else:root.right = Nonereturn root

2.3.3 先序遍历

def pre_order(r):if r is None:return# 根print(r.data, end='')# 左pre_order(r.left)# 右pre_order(r.right)return

2.3.4 中序遍历

def in_order(r):if r is None:return# 左in_order(r.left)# 根print(r.data, end='')# 右in_order(r.right)

2.3.5 后序遍历

def post_order(r):if r is None:return# 左post_order(r.left)# 右post_order(r.right)# 根print(r.data, end='')

2.3.6 完整代码（可运行）

class TreeNode:def __init__(self, data=None, left=None, right=None):self.data = dataself.left = leftself.right = rightdef create_bitree(n, i):  # n = 3root = TreeNode(i)if 2 * i <= n:root.left = create_bitree(n, 2 * i)else:root.left = Noneif 2 * i + 1 <= n:root.right = create_bitree(n, 2 * i + 1)else:root.right = Nonereturn rootdef pre_order(r):if r is None:return# 根print(r.data, end='')# 左pre_order(r.left)# 右pre_order(r.right)returndef in_order(r):if r is None:return# 左in_order(r.left)# 根print(r.data, end='')# 右in_order(r.right)def post_order(r):if r is None:return# 左post_order(r.left)# 右post_order(r.right)# 根print(r.data, end='')n = 3  # 树的节点(编号从1号开始)root = create_bitree(n, 1)
print("前序遍历:")
pre_order(root)
print("\n中序遍历:")
in_order(root)
print("\n后序遍历:")
post_order(root)