Scikit-learn Python机器学习 - 分类算法 - 决策树

锋哥原创的Scikit-learn Python机器学习视频教程：

https://www.bilibili.com/video/BV11reUzEEPH

课程介绍
​

本课程主要讲解基于Scikit-learn的Python机器学习知识，包括机器学习概述，特征工程(数据集，特征抽取，特征预处理，特征降维等)，分类算法(K-临近算法，朴素贝叶斯算法，决策树等)，回归与聚类算法(线性回归，欠拟合，逻辑回归与二分类，K-means算法)等。

Scikit-learn Python机器学习 - 分类算法 - 决策树

决策树（Decision Tree）是一种常见的监督学习算法，用于分类和回归任务。在分类任务中，决策树通过一系列的“决策”来判断一个样本属于哪个类别。其工作原理就像一棵树，树的每个节点表示一个“决策”，树的叶子节点则代表最终的类别标签。

决策树的目标是通过分裂数据来尽可能纯净地划分不同的类别。

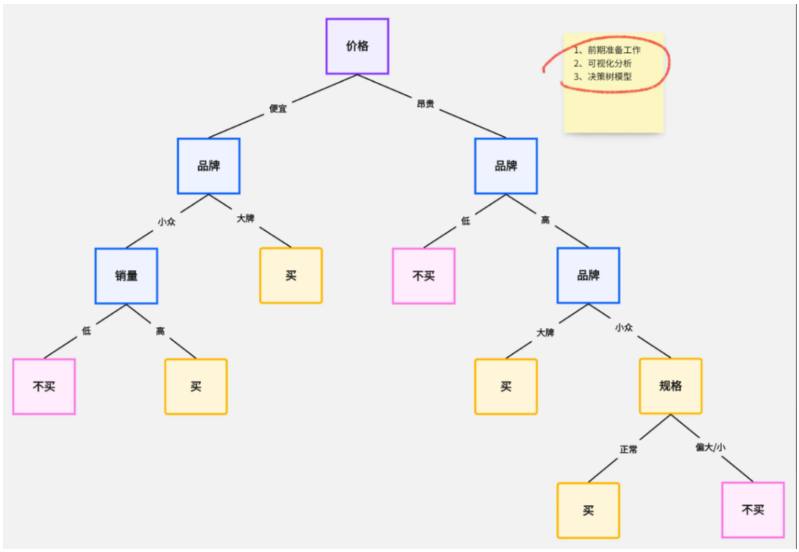
决策树的结构

决策树由根节点、分支节点和叶子节点组成：

1. 根节点：表示整个数据集，包含所有样本。

2. 分支节点：表示特征的决策（如：是/否，真/假等）。

3. 叶子节点：表示最终的类别或预测值。

决策树的工作原理

决策树通过逐层分裂数据，每次选择最能“区分”不同类别的特征来进行分割。它会依据某些准则（如信息增益、基尼系数等）选择最佳的分割特征。

1. 选择最优特征：每次选择一个特征进行划分，目标是使得每一小组的类别尽可能单一（纯度高）。

2. 递归分裂：对每个子集递归地进行上述操作，直到满足停止条件（如树的深度限制、最小样本数限制等）。

3. 生成树结构：最终，树的每个叶子节点代表一个类别。

数学公式：信息增益与基尼系数

1，信息增益（Information Gain）

2，基尼系数（Gini Impurity）

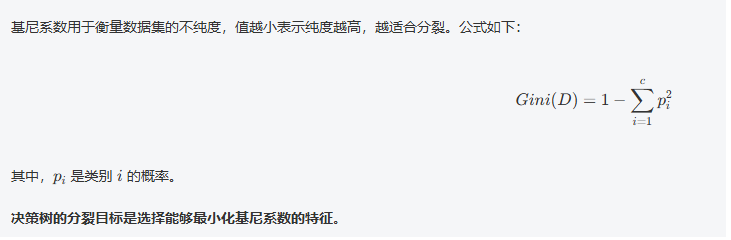
决策树的分裂过程（以信息增益为例）

假设我们有一个包含两个特征 A 和 B 的数据集，目标是根据这两个特征预测目标类别 C。

1. 计算数据集的熵： 首先计算整个数据集的熵（即目标类别的不确定性）。

2. 计算每个特征的条件熵： 对于每个特征（如 A 和 B），计算将数据集按特征值划分后的子集的熵，并加权计算出该特征的条件熵。

3. 计算信息增益： 信息增益是原始数据集的熵减去条件熵。选择信息增益最大的特征进行划分。

4. 递归分裂： 对分裂后的每个子集重复上述步骤，直到所有子集的类别纯度足够高（或达到预设的停止条件）。

具体示例

假设我们有以下数据集：

天气	温度	湿度	风速	类别（是否打球）
晴	热	高	高	否
晴	热	高	低	否
阴	热	高	高	是
雨	温暖	高	高	是
雨	温暖	高	低	是
雨	凉爽	中	高	否
阴	凉爽	中	低	是

我们要预测是否能打球（目标变量）。决策树会依次考察每个特征（天气、温度、湿度、风速）的信息增益，选择最佳特征进行分裂。

1. 计算数据集的熵： 假设类别“是否打球”的分布是 3 个“是”和 4 个“否”，则熵计算如下：

   

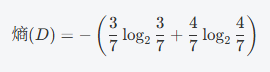
   计算结果为 0.98。

2. 计算信息增益： 假设我们选择“天气”作为第一个特征进行划分，结果是天气的每个取值（晴、阴、雨）对应的子集有不同的熵。我们计算每个子集的熵并加权，得到天气特征的信息增益。

   选择信息增益最大的特征进行分裂，如此递归下去。

具体代码示例

DecisionTreeClassifier 是 scikit-learn 中用于分类任务的决策树模型，它的构造方法（__init__）有多个参数，可以通过这些参数来控制决策树的训练过程和模型复杂度。

DecisionTreeClassifier 构造方法的参数详解：

class sklearn.tree.DecisionTreeClassifier(criterion='gini',splitter='best',max_depth=None,min_samples_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0.0,max_features=None,random_state=None,max_leaf_nodes=None,min_impurity_decrease=0.0,class_weight=None,ccp_alpha=0.0,splitter='best'
)

1. criterion（默认值：'gini'）

• 描述：决定用于选择最佳分裂的质量衡量标准。

• 可选值

  ：

  • 'gini'：基尼系数（Gini Impurity），是衡量数据集不纯度的指标。

  • entropy：信息增益（Information Gain），衡量一个特征分裂数据集后信息的不确定性减少的程度。

• 作用：通过该指标来选择哪个特征的划分最能有效减少数据的不确定性或纯度。

1. splitter（默认值：'best'）

• 描述：决定在每个节点选择分裂特征的策略。

• 可选值

  ：

  • 'best'：每个节点选择最优的特征来分裂。

  • 'random'：每个节点从候选特征中随机选择一个特征来分裂。

• 作用：控制每个节点如何选择用于分裂的特征。'best' 选择最佳的特征，而 'random' 引入了随机性，可能有助于防止过拟合。

1. max_depth（默认值：None）

• 描述：决策树的最大深度，限制树的深度可以防止过拟合。

• 可选值

  ：

  • None：没有限制，树会一直生长，直到所有叶子节点的样本完全纯净或满足停止条件。

  • 任何整数：树的最大深度限制。

• 作用：控制树的复杂度，避免模型过拟合。过大的深度会使得模型过拟合，过小的深度可能导致欠拟合。

1. min_samples_split（默认值：2）

• 描述：在分裂一个节点时，要求每个子节点包含的最小样本数。

• 可选值

  ：

  • 整数：每个节点在进行分裂时，至少需要包含这个数量的样本。

  • 浮动值：表示为样本的比例（0 < min_samples_split < 1），表示每个节点至少需要包含这个比例的样本数。

• 作用：可以防止树的过度生长。如果一个节点的样本数小于该值，就不再继续分裂。

1. min_samples_leaf（默认值：1）

• 描述：每个叶子节点最少包含的样本数。

• 可选值

  ：

  • 整数：叶子节点至少包含的样本数。

  • 浮动值：表示为样本的比例（0 < min_samples_leaf < 1），表示每个叶子节点至少包含这个比例的样本数。

• 作用：可以控制树的复杂度。较大的值会使得叶子节点包含更多样本，有助于防止过拟合。

1. min_weight_fraction_leaf（默认值：0.0）

• 描述：每个叶子节点的最小样本权重和总权重的比值。

• 作用：可以防止训练数据集中某些特定样本的过度影响。一般在样本权重不均时使用。

1. max_features（默认值：None）

• 描述：每次分裂时考虑的特征数量。

• 可选值

  ：

  • None：考虑所有特征进行分裂。

  • 整数：表示在每个节点分裂时考虑的特征数量。

  • 浮动值：表示为特征的比例（0 < max_features < 1），表示每次分裂时选择的特征比例。

  • 'sqrt'：每次分裂时随机选择特征的平方根个数（适用于分类）。

  • 'log2'：每次分裂时随机选择特征的对数个数。

• 作用：限制每次分裂时选择的特征数量，能够有效控制模型的复杂度，尤其是在特征非常多的情况下。

1. random_state（默认值：None）

• 描述：控制随机性，保证实验的可复现性。

• 可选值

  ：

  • None：每次运行时都会生成不同的结果。

  • 整数：固定随机种子，保证每次运行结果相同。

• 作用：当 splitter='random' 或 max_features 设置为随机选择时，使用此参数可以确保结果的可重复性。

1. max_leaf_nodes（默认值：None）

• 描述：树的最大叶子节点数。

• 可选值

  ：

  • None：没有限制，树会一直生长直到满足其他停止条件。

  • 整数：树的最大叶子节点数。

• 作用：限制叶子节点的数量，可以控制树的大小，避免过拟合。

1. min_impurity_decrease（默认值：0.0）

• 描述：每个节点划分时所需的最小不纯度减少量。

• 作用：如果当前节点的划分使得不纯度的减少小于该值，则不再进行划分。

1. class_weight（默认值：None）

• 描述：类别的权重，用于处理类别不平衡问题。

• 可选值

  ：

  • None：所有类别的权重相同。

  • 'balanced'：根据样本的频率自动调整类别权重。

  • 字典：手动指定每个类别的权重。

• 作用：在类别不平衡时，赋予少数类别更大的权重，减少模型的偏向。

1. ccp_alpha（默认值：0.0）

• 描述：用于控制剪枝的复杂度参数。

• 可选值

  ：

  • 0.0：不进行剪枝。

  • 大于0的值：进行剪枝，剪去那些复杂度高而影响泛化性能的子树。

• 作用：通过剪枝来避免过拟合，增加模型的泛化能力。

from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score, classification_report
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier# 1,加载数据
iris = load_iris()
X = iris.data  # 特征矩阵 (150个样本，4个特征：萼长、萼宽、瓣长、瓣宽)
y = iris.target  # 特征值 目标向量 (3类鸢尾花：0, 1, 2)# 2,数据预处理
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)  # 划分训练集和测试集# 3,创建和训练KNN模型
dtc = DecisionTreeClassifier()  # 创建决策树分类器
dtc.fit(X_train, y_train)  # 训练模型# 4,进行预测并评估模型
y_pred = dtc.predict(X_test)  # 在测试集上进行预测
print('决策树预测值：', y_pred)
print('正确值   ：', y_test)accuracy = accuracy_score(y_test, y_pred)  # 计算准确率
print(f'测试集准确率：{accuracy:.2f}')
print('分类报告：\n', classification_report(y_test, y_pred, target_names=iris.target_names))

运行结果：

决策树预测值： [1 1 2 0 0 2 1 1 1 1 2 2 1 2 0 0 1 0 0 1 0 0 0 1 2 2 1 2 2 1]
正确值     ： [1 1 2 0 0 2 1 1 1 1 2 2 1 2 0 0 1 0 0 1 0 0 0 1 2 2 1 2 2 2]
测试集准确率：0.97
分类报告：precision    recall  f1-score   supportsetosa       1.00      1.00      1.00         9versicolor       0.92      1.00      0.96        11virginica       1.00      0.90      0.95        10accuracy                           0.97        30macro avg       0.97      0.97      0.97        30
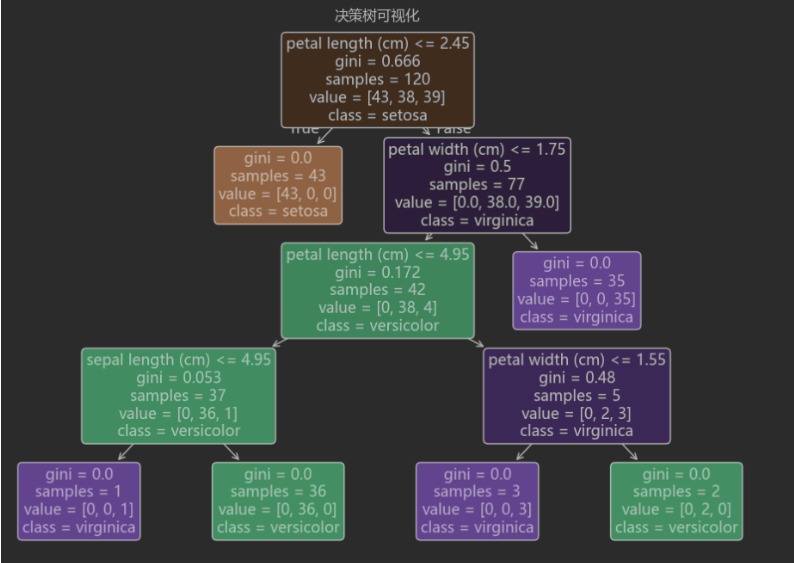
weighted avg       0.97      0.97      0.97        30

决策树可视化

结合matplotlib实现决策树可视化，这样更直观，方便直观的看到具体算法数据。

先安装下matplotlib库以及jupyter库：

pip install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple

pip install jupyter -i https://pypi.tuna.tsinghua.edu.cn/simple

新建DecisionTreeClassifierTest.ipynb文件。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
​
# 1,加载数据
iris = load_iris()
X = iris.data  # 特征矩阵 (150个样本，4个特征：萼长、萼宽、瓣长、瓣宽)
y = iris.target  # 特征值 目标向量 (3类鸢尾花：0, 1, 2)
​
# 2,数据预处理
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)  # 划分训练集和测试集
​
# 3,创建和训练KNN模型
dtc = DecisionTreeClassifier()  # 创建决策树分类器
dtc.fit(X_train, y_train)  # 训练模型
​
import matplotlib
from sklearn.tree import plot_tree
from matplotlib import pyplot as plt
​
# 设置matplotlib使用黑体显示中文
matplotlib.rcParams['font.family'] = 'Microsoft YaHei'
​
# 可视化决策树
plt.figure(figsize=(12, 8))
plot_tree(dtc,filled=True,feature_names=iris.feature_names,class_names=iris.target_names,rounded=True
)
plt.title("决策树可视化")
plt.show()

运行结果：