当前位置：首页 > news >正文

动态规划-详解回文串系列问题

news 2025/9/18 6:43:02

一、最长回文子串（LeetCode 5）

二、回文子串计数（LeetCode 647）

三、分割回文串系列

1. 分割回文串 IV（LeetCode 1745）

2. 分割回文串 II（LeetCode 132）

四、最长回文子序列（LeetCode 516）

五、让字符串成为回文串的最少插入次数（LeetCode 1312）

总结

回文串是字符串算法中的经典主题，涉及“最长回文子串”“回文子串计数”“分割回文串”等多个变种问题。这类问题的核心是利用动态规划挖掘子问题的递推关系，下面逐一解析其解题思路。

一、最长回文子串（LeetCode 5）

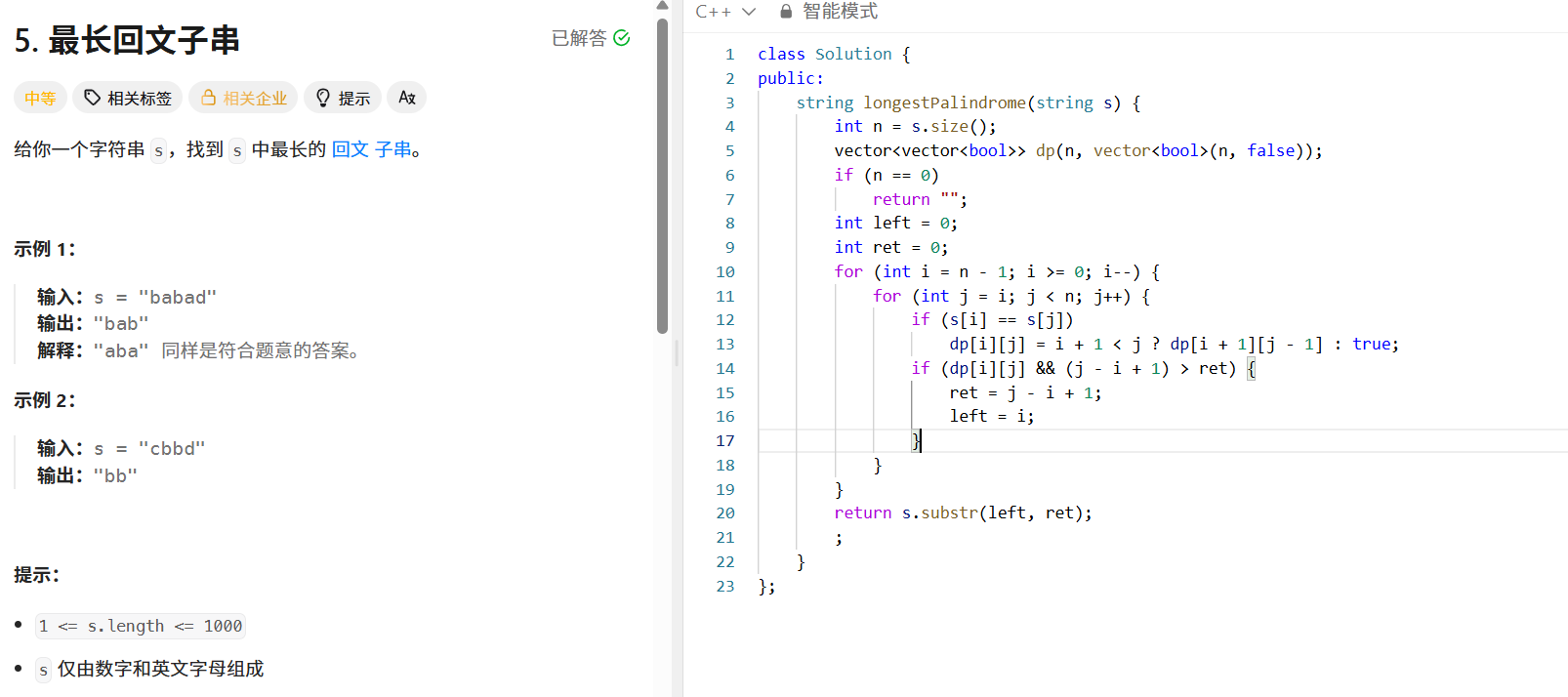
问题：给定字符串 s ，找出最长的连续回文子串。

动态规划思路

- 状态定义： dp[i][j]  表示子串 s[i..j]  是否为回文串（ true/false ）。
- 状态转移：
- 若 s[i] == s[j] ，则 dp[i][j]  由 dp[i+1][j-1]  决定（子串内部是否回文）。
- 边界情况：当 i == j （子串长度为1）时， dp[i][j] = true ；当 j = i+1 （子串长度为2）时， dp[i][j] = (s[i] == s[j]) 。
- 结果记录：遍历过程中记录最长回文串的起始位置 left  和长度 ret 。

代码核心逻辑

vector<vector<bool>> dp(n, vector<bool>(n, false));
int left = 0, ret = 0;
for (int i = n - 1; i >= 0; i--) {for (int j = i; j < n; j++) {if (s[i] == s[j]) {dp[i][j] = (i + 1 < j) ? dp[i+1][j-1] : true;if (dp[i][j] && (j - i + 1) > ret) {ret = j - i + 1;left = i;}}}
}
return s.substr(left, ret);

二、回文子串计数（LeetCode 647）

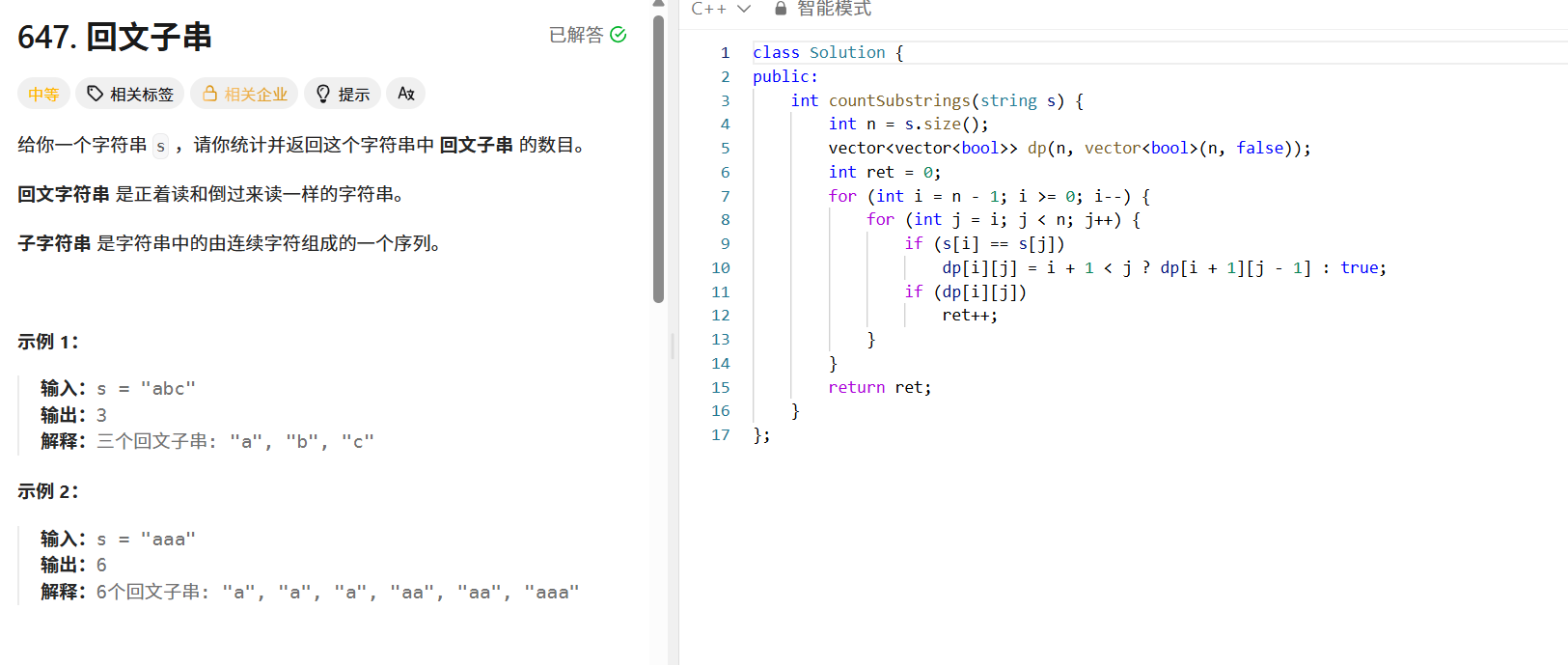
问题：统计字符串中所有回文子串的数量。

动态规划思路

- 状态定义：与“最长回文子串”一致， dp[i][j]  表示 s[i..j]  是否为回文串。
- 状态转移：同上述逻辑，若 s[i] == s[j] ，则 dp[i][j]  由 dp[i+1][j-1]  推导。
- 结果统计：每当 dp[i][j] == true  时，计数器加一。

代码核心逻辑

vector<vector<bool>> dp(n, vector<bool>(n, false));
int ret = 0;
for (int i = n - 1; i >= 0; i--) {for (int j = i; j < n; j++) {if (s[i] == s[j]) {dp[i][j] = (i + 1 < j) ? dp[i+1][j-1] : true;if (dp[i][j]) ret++;}}
}
return ret;

三、分割回文串系列

这类问题的关键是先预处理所有子串是否为回文，再结合具体分割要求推导。

1. 分割回文串 IV（LeetCode 1745）

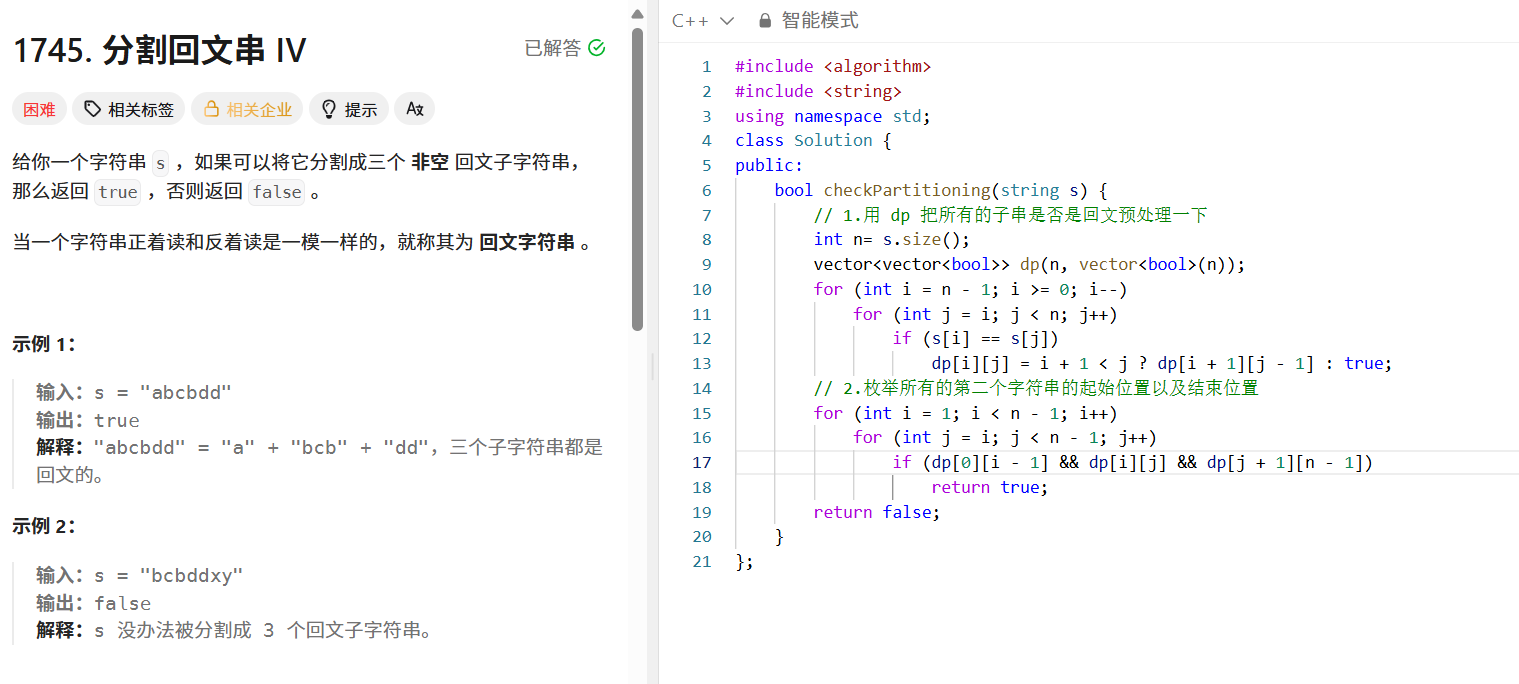
问题：判断字符串能否分割成三个非空回文子串。

解题步骤

- 步骤1：预处理回文子串：用动态规划得到 dp[i][j] （ s[i..j] 是否为回文）。
- 步骤2：枚举分割点：枚举第二个回文子串的起止位置 i 和 j ，验证三个分段 s[0..i-1] 、 s[i..j] 、 s[j+1..n-1] 是否均为回文。

代码核心逻辑


vector<vector<bool>> dp(n, vector<bool>(n, false));
// 预处理回文子串
for (int i = n - 1; i >= 0; i--) {for (int j = i; j < n; j++) {if (s[i] == s[j]) {dp[i][j] = (i + 1 < j) ? dp[i+1][j-1] : true;}}
}
// 枚举第二个子串的分割点
for (int i = 1; i < n - 1; i++) {for (int j = i; j < n - 1; j++) {if (dp[0][i-1] && dp[i][j] && dp[j+1][n-1]) {return true;}}
}
return false;

2. 分割回文串 II（LeetCode 132）

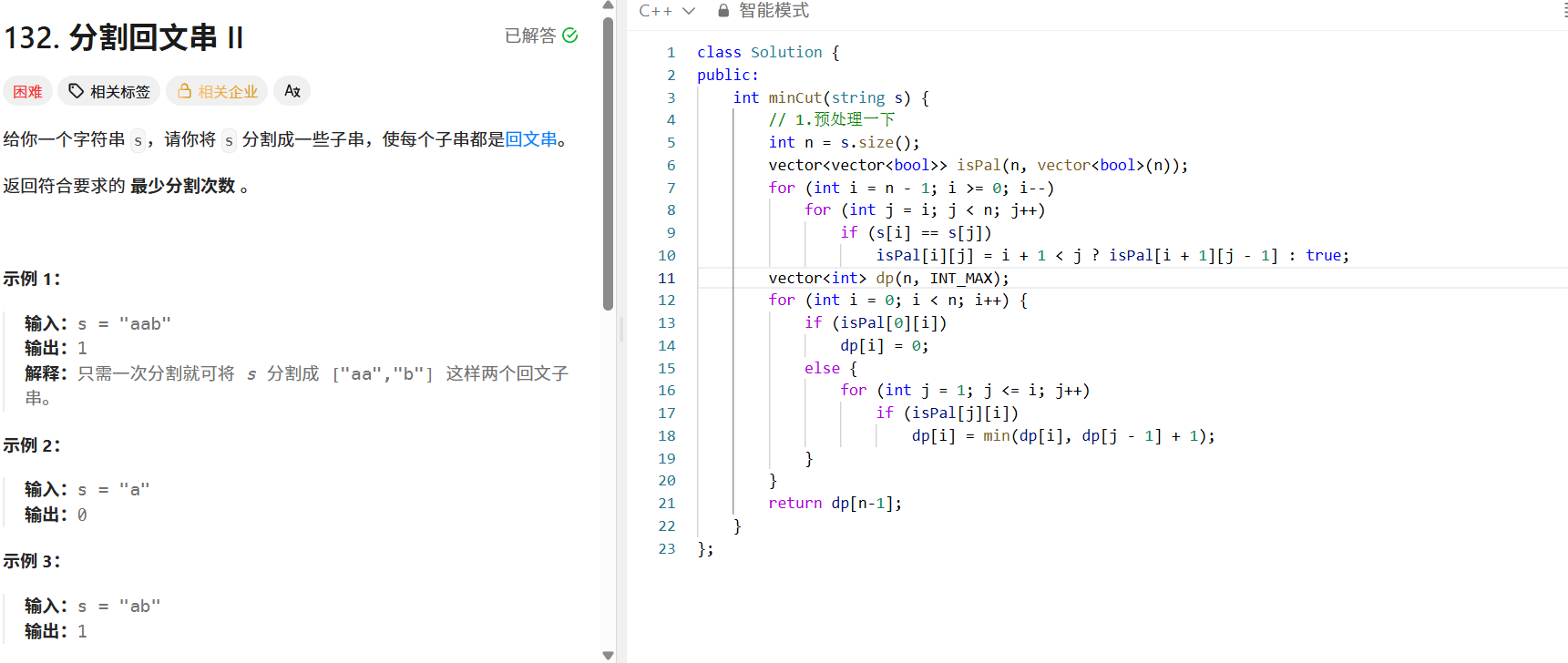
问题：求将字符串分割为全回文子串的最少分割次数。

解题步骤

- 步骤1：预处理回文子串：得到 isPal[i][j] （ s[i..j]  是否为回文）。
- 步骤2：动态规划求最少分割次数：定义 dp[i]  为 s[0..i]  的最少分割次数。
- 若 s[0..i]  本身是回文，则 dp[i] = 0 。
- 否则，枚举分割点 j ，若 s[j..i]  是回文，则 dp[i] = min(dp[i], dp[j-1] + 1) 。

代码核心逻辑

vector<vector<bool>> isPal(n, vector<bool>(n, false));
// 预处理回文子串
for (int i = n - 1; i >= 0; i--) {for (int j = i; j < n; j++) {if (s[i] == s[j]) {isPal[i][j] = (i + 1 < j) ? isPal[i+1][j-1] : true;}}
}
vector<int> dp(n, INT_MAX);
for (int i = 0; i < n; i++) {if (isPal[0][i]) {dp[i] = 0;} else {for (int j = 1; j <= i; j++) {if (isPal[j][i]) {dp[i] = min(dp[i], dp[j-1] + 1);}}}
}
return dp[n-1];

四、最长回文子序列（LeetCode 516）

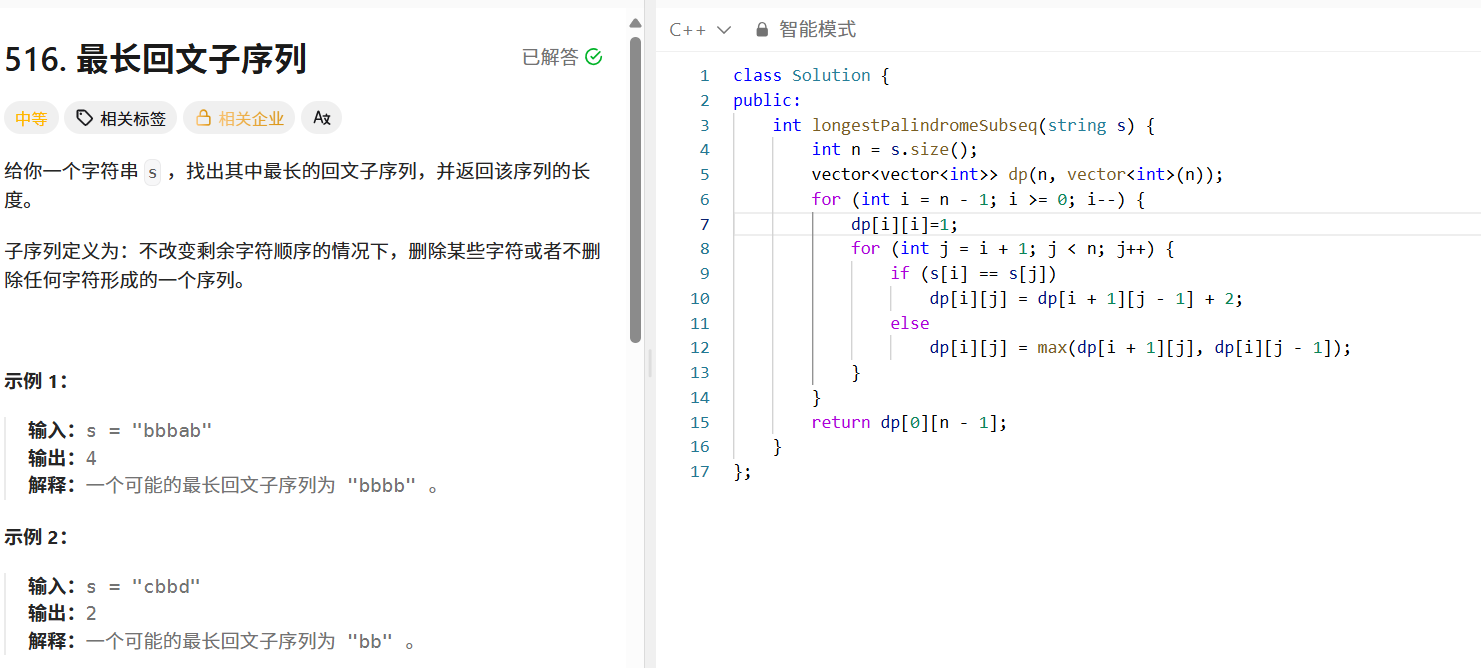
问题：找出最长的回文子序列（子序列不要求连续）。

动态规划思路

- 状态定义： dp[i][j] 表示 s[i..j] 中最长回文子序列的长度。
- 状态转移：
- 若 s[i] == s[j] ，则 dp[i][j] = dp[i+1][j-1] + 2 （两端字符加入子序列）。
- 否则， dp[i][j] = max(dp[i+1][j], dp[i][j-1]) （取子问题的最大值）。
- 边界条件： dp[i][i] = 1 （单个字符的子序列长度为1）。

代码核心逻辑

vector<vector<int>> dp(n, vector<int>(n, 0));
for (int i = n - 1; i >= 0; i--) {dp[i][i] = 1;for (int j = i + 1; j < n; j++) {if (s[i] == s[j]) {dp[i][j] = dp[i+1][j-1] + 2;} else {dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}
}
return dp[0][n-1];

五、让字符串成为回文串的最少插入次数（LeetCode 1312）

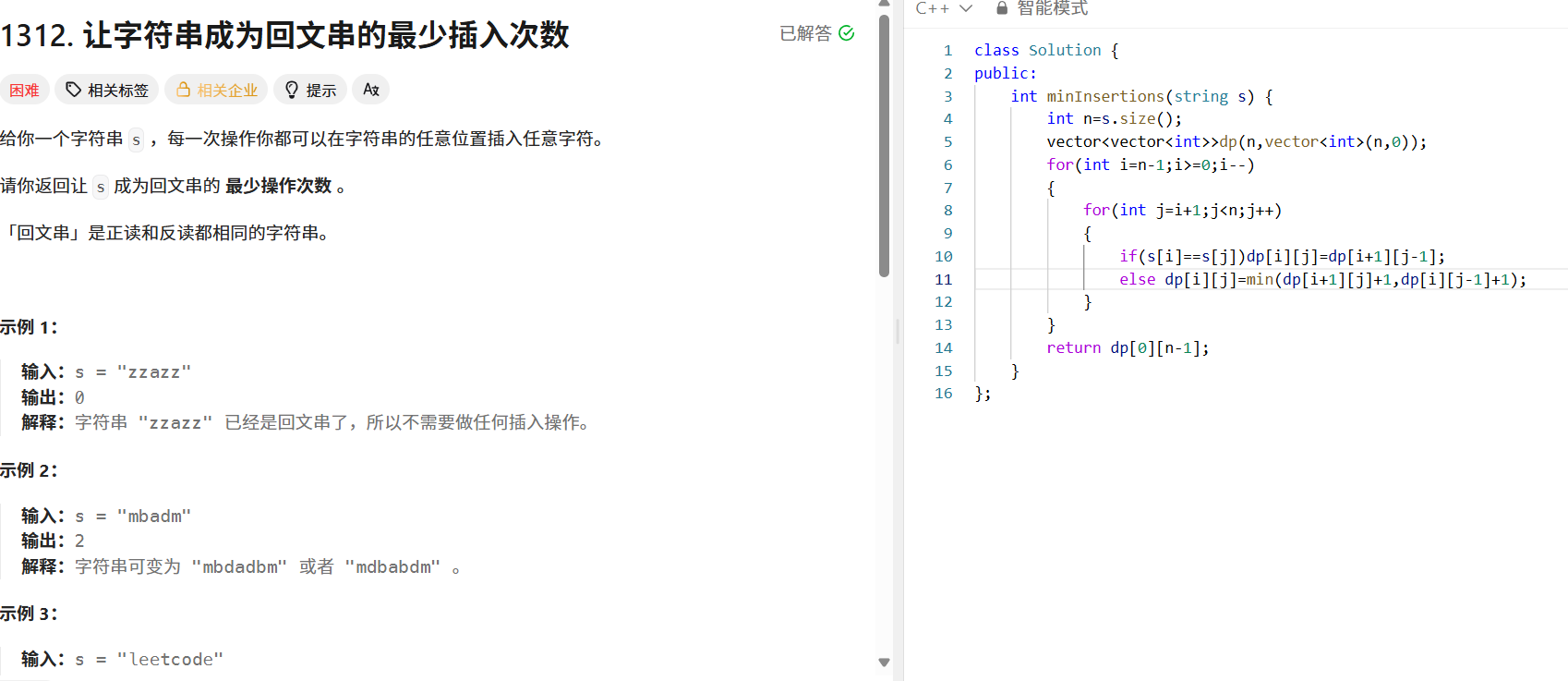
问题：通过插入字符使字符串成为回文，求最少插入次数。

动态规划思路

- 状态定义： dp[i][j] 表示将 s[i..j] 变为回文的最少插入次数。
- 状态转移：
- 若 s[i] == s[j] ，则 dp[i][j] = dp[i+1][j-1] （无需插入，继承子问题结果）。
- 否则， dp[i][j] = min(dp[i+1][j] + 1, dp[i][j-1] + 1) （在左端或右端插入字符，取次数较少的方案）。

代码核心逻辑

vector<vector<int>> dp(n, vector<int>(n, 0));
for (int i = n - 1; i >= 0; i--) {for (int j = i + 1; j < n; j++) {if (s[i] == s[j]) {dp[i][j] = dp[i+1][j-1];} else {dp[i][j] = min(dp[i+1][j] + 1, dp[i][j-1] + 1);}}
}
return dp[0][n-1];