机器人工具标定-记录一下-待验证(没数据)
最近看手眼标定,先把工具标定的原理先理顺一下
核心原理是:标定点尖端在基座坐标系下的位置是不变的,所以4个点可以列出三个等式方程,先求相对位置,再指定方向;
尖端相对位置 * 旋转矩阵 + 末端法兰坐标 = 尖端基座坐标系(等式右边恒等)
1.工具标定往往使用6点法
前三个点是用不同姿态的三个点指向固定的尖端
第四个点是垂直方向的点
第五个点是工具X轴方向的点
第6个点是工具Z轴方向的点
2.前四个点计算尖端点的位置相对于法兰末端的相对坐标,即deltX deltY deltZ
3.第五个点减第四个点方向为X轴轴向
4.第6个点减第四个点方向位Z轴轴向
5.Y方向为Z叉乘X得到的方向
6.向量归一化+deltX deltY deltZ得到工具的转换矩阵
原理:参考论文【基于线激光相机视觉引导的焊接技术研究】 我把原理图直接从论文里粘贴一下



完全按照上面的公式往下理应该是没啥问题,需要注意的列出:
1.前四个点,构建旋转矩阵的时候,需要看下机器人是哪种旋转模式,论文里是ZYX顺序,常见的是XYZ(勃朗特+新松等),需要注意一下
2.4个点能构建的等式是93 33 = 93,按照这个格式构建一下
3.等式类似AX=B,但A是9*3(系数矩阵秩一般等于3 ,为列满秩矩阵。式为不相容方程组),没有逆矩阵,没法直接用,需要求A的广义逆矩阵,如下
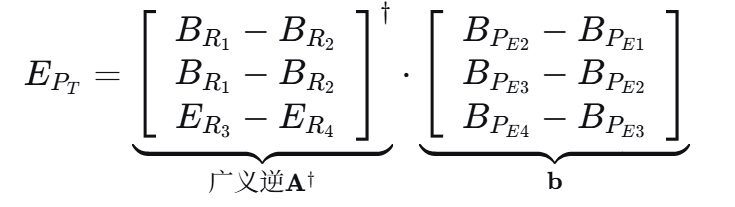
求广义逆矩阵,可以看公式,或者借助Eigen矩阵库,下面代码是粘贴的,没有经过验证,有数据的可以验证一下
博客:利用Eigen求广义逆矩阵

Eigen::MatrixXd MainWindow::pinv(Eigen::MatrixXd A)
{Eigen::JacobiSVD<Eigen::MatrixXd> svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);double pinvtoler = 1.e-8; //toleranceint row = A.rows();int col = A.cols();int k = min(row,col);Eigen::MatrixXd X = Eigen::MatrixXd::Zero(col,row);Eigen::MatrixXd singularValues_inv = svd.singularValues();//奇异值Eigen::MatrixXd singularValues_inv_mat = Eigen::MatrixXd::Zero(col, row);for (long i = 0; i<k; ++i) {if (singularValues_inv(i) > pinvtoler)singularValues_inv(i) = 1.0 / singularValues_inv(i);else singularValues_inv(i) = 0;}for (long i = 0; i < k; ++i) {singularValues_inv_mat(i, i) = singularValues_inv(i);}X=(svd.matrixV())*(singularValues_inv_mat)*(svd.matrixU().transpose());return X;}
原理就这样,手头没数据,有数据的可以测试一下
