算法 --- 队列 + 宽搜(BFS)
队列 + 宽搜(BFS)
当题目涉及“层级扩展”、“最短路径”或“状态转换的最小步数”时,就应该使用队列+宽搜(BFS)。
队列 + 宽搜(BFS)算法主要适用于解决那些需要按层次遍历或寻找无权图最短路径的问题。其核心思想是从一个起点出发,逐层地、均匀地向所有可能的方向探索,确保第一次到达目标时的路径就是最短的。具体适用于以下几类题目:
-
树/图的层级遍历:例如二叉树的层序遍历,或需要按距离起点第K层的所有节点。
-
迷宫/网格最短路径:在二维网格中,从起点到终点,避开障碍物,求移动的最小步数(每次可上下左右移动一格)。这是最经典的BFS应用场景。
-
最小转换步数问题:题目将一种状态(如一个字符串、一个数组配置)通过一系列规则转换为目标状态,求所需的最小操作次数。例如“滑动谜题”、“打开转盘锁”等,每个状态可以看作图的一个节点,一次操作就是连接节点的边。
-
连通块问题:需要找出一个平面或图中所有连通的区域(如岛屿问题),BFS可以有效地遍历并标记整个区域。
为什么用队列?
因为队列“先进先出”(FIFO)的特性完美契合了BFS“先来的先扩展”的需求。它保证了先被访问的节点(离起点更近的层)永远先于后被访问的节点(离起点更远的层)得到处理,从而确保了找到最短路径的正确性。
总结:只要你看到题目要求“最短”、“最少步数”、“按层展开”,你的第一反应就应该是队列+BFS。
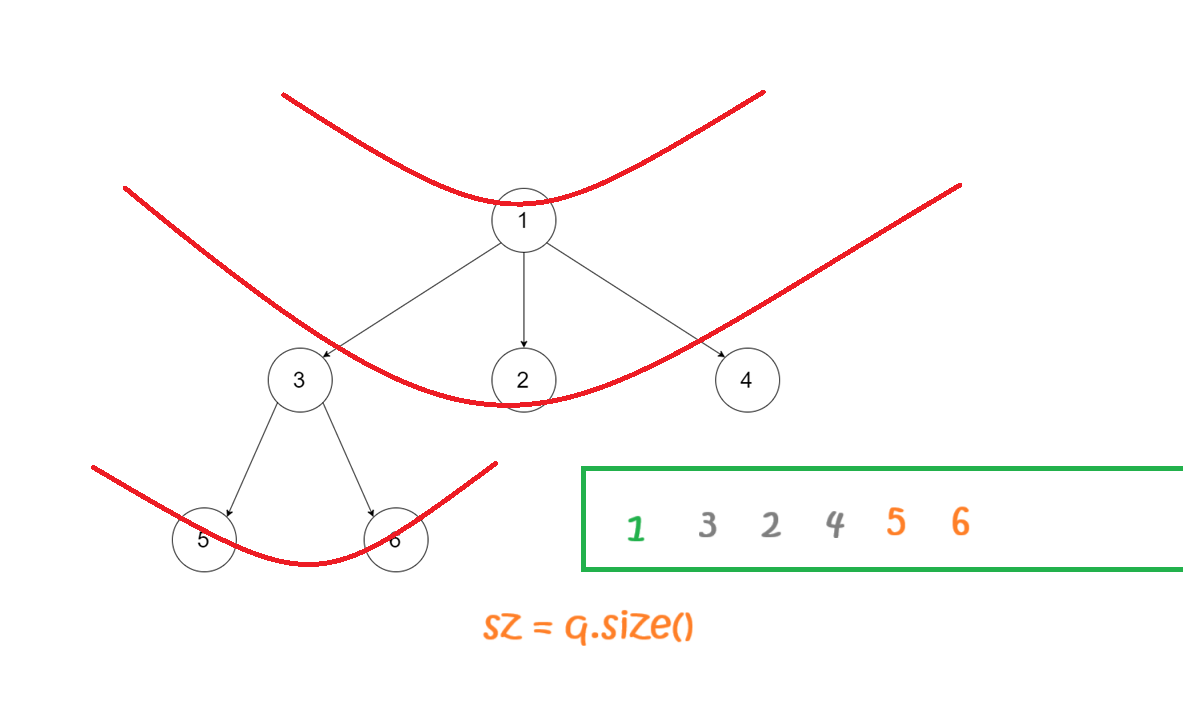
基本的框架就是:
XXX bfs (Node* root) {queue<Node*> q;if(root == nullptr) return ???;q.push(root);while(q.size()){// int sz = q.size();vector<int> tmp;//while(sz--)//{Node* t = q.front();q.pop();//}}return ???
}题目练习
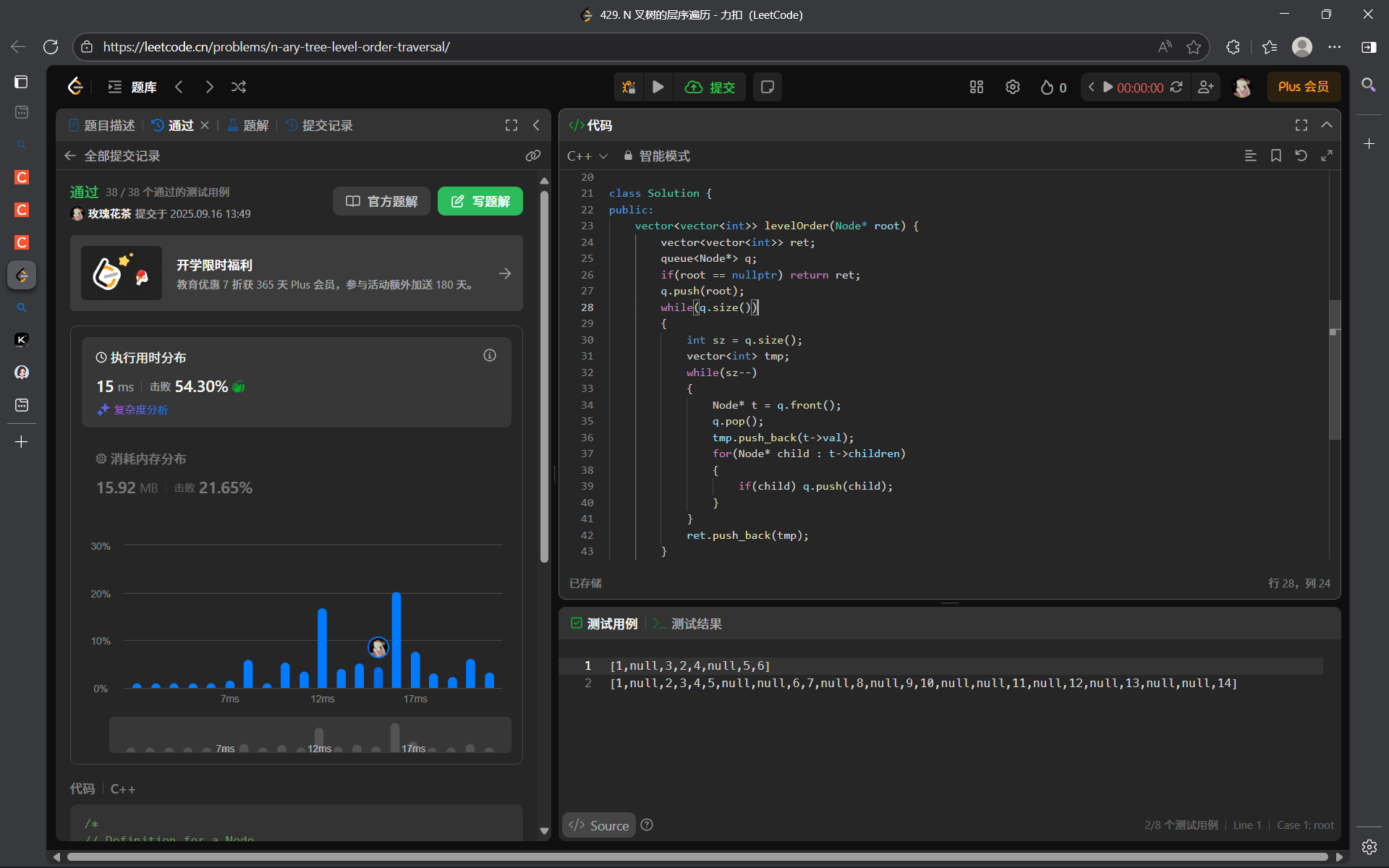
429. N 叉树的层序遍历 - 力扣(LeetCode)
解法:
算法思路:
层序遍历即可~
仅需多加一个变量,用来记录每一层结点的个数就好了。
class Solution {
public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret;queue<Node*> q;if(root == nullptr) return ret;q.push(root);while(q.size()){int sz = q.size();vector<int> tmp;while(sz--){Node* t = q.front();q.pop();tmp.push_back(t->val);for(Node* child : t->children){if(child) q.push(child);}}ret.push_back(tmp);}return ret;}
};
103. 二叉树的锯齿形层序遍历 - 力扣(LeetCode)
解法(层序遍历):
算法思路:
在正常的层序遍历过程中,我们是可以把一层的结点放在一个数组中去的。
既然我们有这个数组,在合适的层数逆序就可以得到锯齿形层序遍历的结果。
class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> ret;if(root == nullptr) return ret;queue<TreeNode*> q;q.push(root);bool flag = true;//正序while(q.size()){int sz = q.size();vector<int> tmp;while(sz--){auto t = q.front();q.pop();tmp.push_back(t->val);if(t->left) q.push(t->left);if(t->right) q.push(t->right);}if(!flag) reverse(tmp.begin(), tmp.end());flag = !flag;ret.push_back(tmp);}return ret;}
};
662. 二叉树最大宽度 - 力扣(LeetCode)
解法(层序遍历):
算法思路:
-
第一种思路(会超过内存限制):
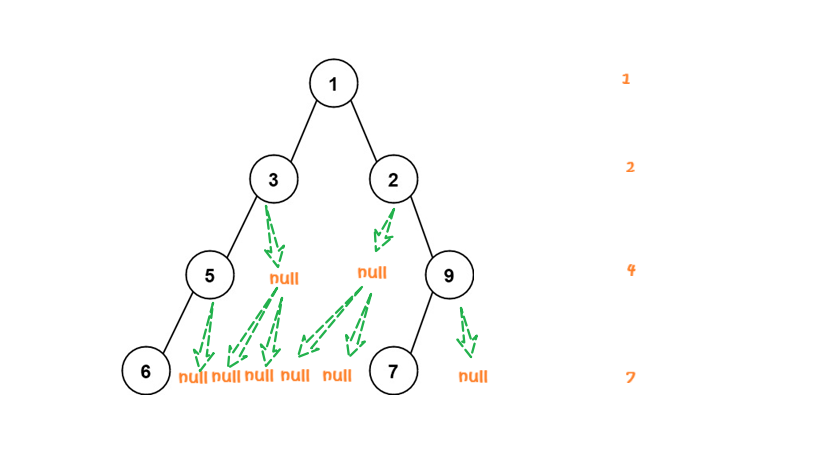
既然统计每一层的最大宽度,我们优先想到的就是利用层序遍历,把当前层的结点全部存在队列里面,利用队列的长度来计算每一层的宽度,统计出最大的宽度。
但是,由于空节点也是需要计算在内的。因此,我们可以选择将空节点也存在队列里面。
这个思路是我们正常会想到的思路,但是极端情况下,最左边一条长链,最右边一条长链,我们需要存几个空节点,会超过最大内存限制。
-
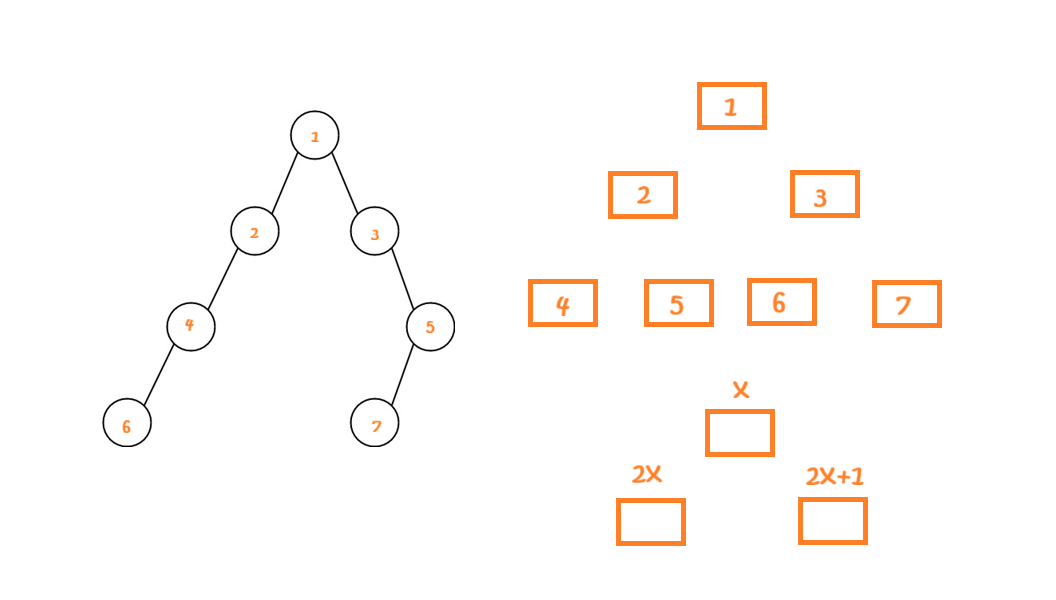
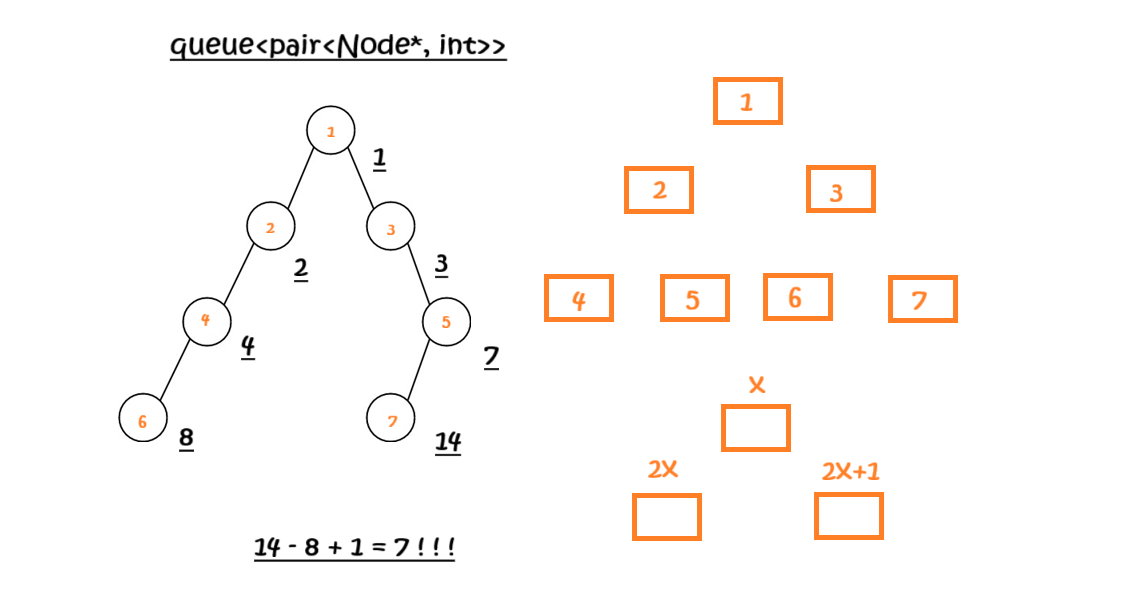
第二种思路(利用二叉树的顺序存储 - 通过根节点的下标,计算左右孩子的下标):
依旧是利用层序遍历,但是这一次队列里面不单单存结点信息,并且还存储当前结点如果在数组中存储所对应的下标(在我们学习数据结构 - 堆的时候,计算左右孩子的方式)。
这样我们计算每一层宽度的时候,无需考虑空节点,只需将当层结点的左右结点的下标相减再加 1 即可。
但是,这里有个细节问题:如果二叉树的层数非常恐怖的话,我们任何一种数据类型都不能存下下标的值。但是没有问题,因为:
-
我们数据的存储是一个环形的结构;
-
并且题目说明,数据的范围在
int这个类型的最大值的范围之内,因此不会超出一圈; -
因此,如果是求差值的话,我们无需考虑溢出的情况。
-
class Solution {
public:int widthOfBinaryTree(TreeNode* root) {vector<pair<TreeNode*, unsigned int>> q;q.push_back({root, 1});unsigned int ret = 0;while(q.size()){auto& [x1, y1] = q[0];auto& [x2, y2] = q.back();ret = max(ret, y2 - y1 + 1);vector<pair<TreeNode*, unsigned int>> tmp;for(auto& [x, y] : q){if(x->left) tmp.push_back({x->left, y * 2});if(x->right) tmp.push_back({x->right, y * 2 + 1});}q = tmp;}return ret;}
};
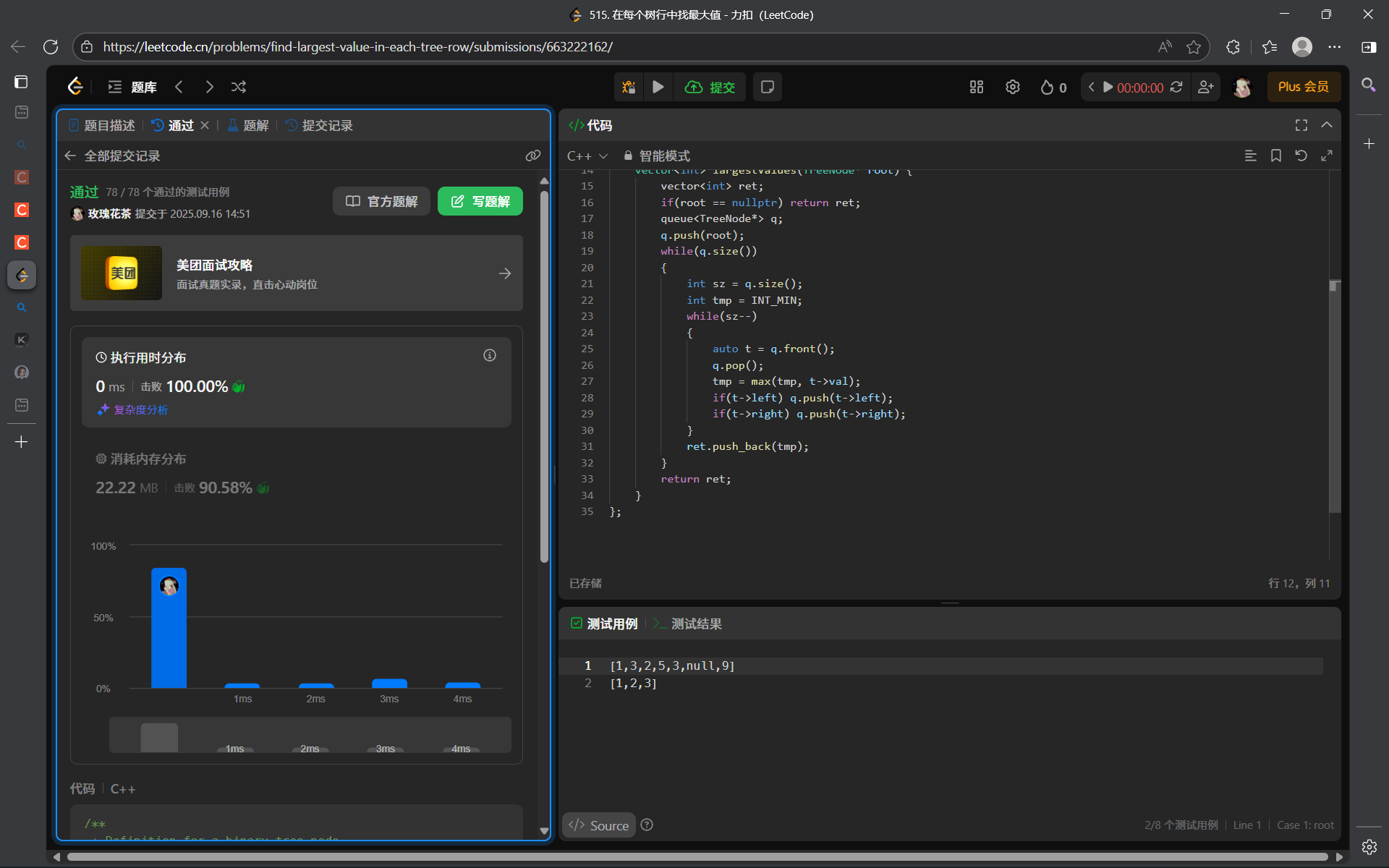
515. 在每个树行中找最大值 - 力扣(LeetCode)
解法(BFS):
算法思路:
层序遍历过程中,在执行让下一层节点入队的时候,我们是可以在循环中统计出当前层结点的最大值的。
因此,可以在 BFS 的过程中,统计出每一层结点的最大值。
class Solution {
public:vector<int> largestValues(TreeNode* root) {vector<int> ret;if(root == nullptr) return ret;queue<TreeNode*> q;q.push(root);while(q.size()){int sz = q.size();int tmp = INT_MIN;while(sz--){auto t = q.front();q.pop();tmp = max(tmp, t->val);if(t->left) q.push(t->left);if(t->right) q.push(t->right);}ret.push_back(tmp);}return ret;}
};