当前位置：首页 > news >正文

机器人导论第六章动力学（1）——牛顿欧拉法推导与详述

news 2025/9/17 7:52:50

机器人动力学分析复习速通

机器人分析分为

牛顿欧拉法、拉格朗日法、高斯法、凯恩方法

matlab提供的逆动力学采用的是牛顿欧拉法：RNE——Recursive Newton-Euler

需要三个参数，第一个是给定最终的角度，第二个是速度，第三个是角加速度，返回各个关节所需要的力矩。
可选参数有重力加速度和负载fext

牛顿欧拉法

我们的目标是给定机器人的关节位置 q、速度 qd 和加速度 qdd，计算出为了产生这个运动状态，每个关节需要施加多大的驱动力矩 。

一上来看到有人问——我们不是用力域雅可比解决了每个关节应该分配多大力矩的问题了吗？

这是我初学的时候也弄混的问题。

“力域雅可比”解决的是一个不同的问题，属于静力学或外力映射范畴，他的目的是将作用在机器人末端执行器上的外力/力矩映射到对应的关节空间力矩。

区别就是一个是给定运动状态，计算每个关节为了达到这个运动状态需要多大力；
另一个则是给定末端的力，计算这个力分配在各个关节上是多大。

牛顿欧拉法的精髓在于正推和逆推，我们来看这个过程：

正向递推（Forward Recursion）：从基座到末端，计算每个连杆的速度、加速度。
反向递推（Backward Recursion）：从末端到基座，计算每个关节需要提供的力和力矩。

我们先大概浏览一遍整个过程，这里看不懂也没关系，大概有个流程印象即可！
我们快速总结一下：
动力学的目的就是计算在某个运动状态下，各个关节应该施加多大的力，因此核心是构建一个“运动状态-力学参数”的方程，牛顿和欧拉两位大佬就提供了。
我们的核心就变成了如何得到各个关节的“真实速度”。
我们已知各个关节的关节空间的速度、角速度、加速度，如何将前一个坐标系的运动参数传递给下一个坐标系计算呢？
这就用到了正推，构建线速度、线加速度、角速度、角加速度以及质心和端点的速度关系。
这里面最难理解的就是对Zi轴的求导，我们把求导拆成先微分再对时间求导，并用红蓝绿坐标系表示了这个过程。
最终得到了运动参数的递推公式。

我们又知道，力的传播是从末端向基座的，因此力的计算就是逆推的过程。
我们先对连杆的相互作用点进行了受力分析，并构建了端点到质心的变换公式，得以计算质心处的合力矩情况。
此时的合力矩指的是xyz三方向的合力矩，但是关节电机只能控制绕z轴旋转的力矩，因此我们将合力矩中的Z方向力矩提取出来，直接用Z的方向向量点积即可。
由此，我们就能通过得知各个关节的关节速度、加速度，从而推导出各个关节需要多大的力矩了！

那么构建运动状态和力的关系的等式就显而易见了：

牛顿方程： $F_i = m \dot{\mathbf{v}}_{C_i}$

用于解决刚体平移的动力学刻画，沟通力与线加速度的关系。

欧拉方程： $N_i = \mathbf{c}_i I \dot\omega_i + \omega_i \times \mathbf{c}_i I \omega_i$

用于解决刚体旋转的动力学刻画，沟通力矩与角速度、角加速度的关系。

欧拉方程具体是如何推导的请参考：【机器人学 3.5 牛顿欧拉递推动力学算法前置知识3】 https://www.bilibili.com/video/BV1Re41127pq/?share_source=copy_web&vd_source=2c56c6a2645587b49d62e5b12b253dca

不看不影响，暂且把它当作和牛顿方程一样的给定式。

其中， $_{}^{C}\textrm{I}$ 是刚体在{C}中的惯性张量。惯性张量矩阵求法可以参考【】

那么要得到连杆质心的力和力矩，就必须要求线加速度、角速度、角加速度了。

由于串联机械臂具有强耦合关系，因此相邻关节之间存在一定递推关系。假设你在旋转肩膀的同时转动胳膊，定义肩膀的角速度ω1，胳膊的角速度ω2，此时，你胳膊的实际角速度并非ω2，而是一个与肩膀角速度相关的函数，意味着当前连杆的运动状态依赖于前一个连杆的运动参数。递推法就是计算当前连杆真实运动状态的方法。

正推

首先对连杆1进行计算，然后利用递推式，就能得知连杆2的运动状态直至关节n。

我们只关心相邻连杆的运动状态关系：

旋转运动参数

角速度

对于角速度：

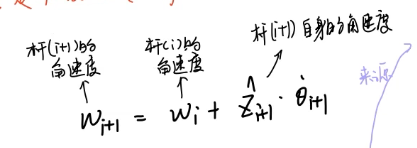
这个式子很好理解，地球自转的同时也绕着太阳公转，因此真实的角速度是公转速度+自转速度。在这里，wi指前一个关节的角速度，即绕太阳的公转速度，第二项是地球绕地轴Zi+1的自转速度。

角加速度

对于角加速度：

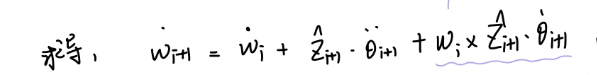
角加速度无非是对角速度求时间的微分。
第一项求导很正常。
第二项求导要注意，是乘积求导法则。对于速度 $\dot\theta$ 求导没问题，重点在于如何对 $\hat{Z}_{i+1}$ 求导

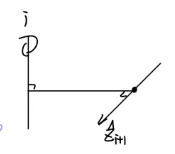
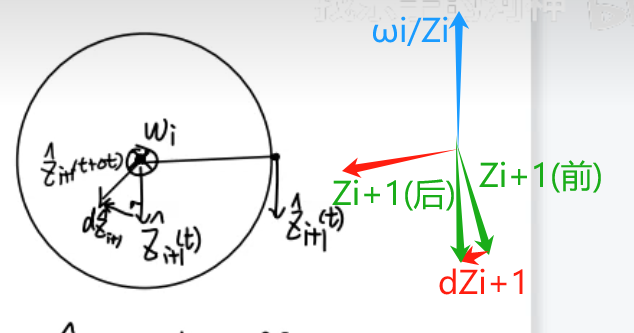
为了简化计算，我们不妨设 $Z_{i}$ 和 $Z_{i+1}$ 互相垂直，那么根据下图，此时的 $d\hat{Z}_{i+1}$ 表示 $\hat{Z}_{i+1}$ 离原来偏移了多少，就可以用 $\hat{Z}_{i+1}$ 与 $\hat{Z}_{i}$ 叉积表示了！

$\hat{Z}_{i+1}$ 前 X $\hat Z_{i}$ 的结果就是最大的红色箭头。假设经过dt后 $\hat{Z}_{i+1}$ 从（前）变到（后），此时 $d\hat{Z}_{i+1}$ 正好与叉积结果平行！

叉积就是乘以sin，于是有：

$|dZ_{i+1}|=|Z_{i+1}|\cdot |\omega_i|\cdot dt \cdot sin(\frac{\pi}{2})$
对于dt求导
$\frac{dZ_{i+1}}{dt}=Z_{i+1} \times \omega_i$

这就是第三项的来源！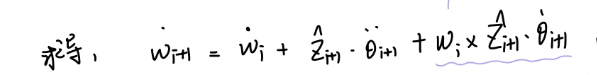

接着，由于我们是根据i系的运动状态计算i+1系的运动参数，因此要把所有参数转入{i+1}系中：
同时利用旋转矩阵（{i}系与{i+1}系的旋转矩阵）将所有参数的上下标统一：

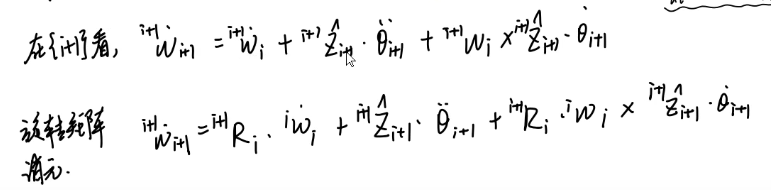
平移运动参数

线速度

线速度不仅会由前一个连杆传递（即便前一个连杆不存在平移，也可能继承了前前个平移关节的线速度）；
如果前一个连杆是旋转关节，由于存在连杆长度R，必然会产生由旋转而产生的线速度 $v_{rotate}=\omega \times R$ 也就是 角速度X半径：

这个 $P^*_{i+1}$ 是指{i}系原点指向{i+1}系原点的向量，也就是连杆长度。

线加速度

同理，求加速度就是对速度求时间的微分。
第一项求导很正常。
第二项求导要注意，是乘积求导法则。

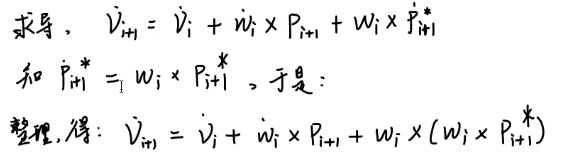
$\dot P^*_{i+1}=w_i \times P^*_{i+1}$ 是显然的线速度就是 角速度X半径嘛

把 $\dot P^*_{i+1}$ 替换进求导的式子，得到上式。

接着，先将各参数转入{i}参考系，再用{i}系与{i+1}系的旋转矩阵 $_{}^{i+1}\textrm{R}_{i}$ 将运动参数转入{i+1}系中。

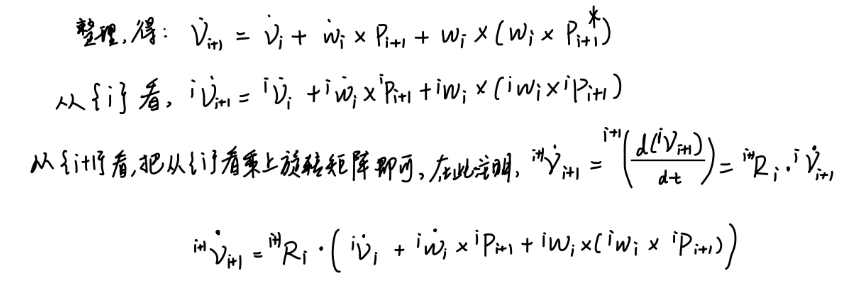
从质心到关节的变换

上面我们刻画了质心的运动参数递推关系，但是在实际控制中，我们肯定控制的是关节，因此还需要将质心处的参数变换到关节上：

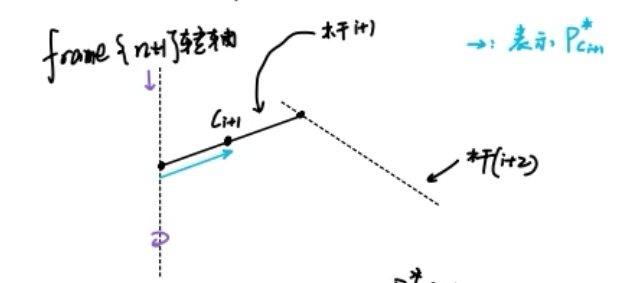
线速度

规定关节坐标系原点指向质心的向量为 $P^*_{C_{i+1}}$ ，那么这显然是一个类似“平移”的操作，因此套用线速度的递推公式：

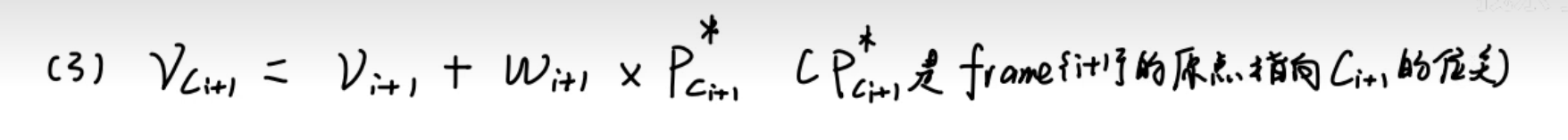
线加速度

同理求导，下式关系显然满足（旋转引起的线速度=角速度X半径）。

因此求导可得：

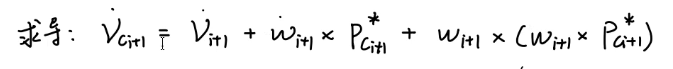
同理，将其转入{i+1}系：

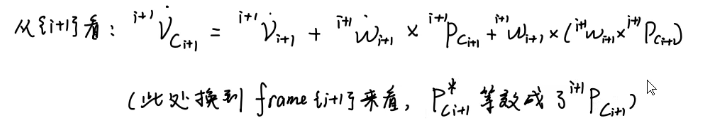
这就是书上这几个不给推导/引用链比你还长的式子的简要理解：

注：
书上的推导是严谨的，但是深邃难懂，我也是二刷才看懂，而且引经据典到6.15式，6.15有引用6.6式，6.6式又引用5.12式等，引用链复杂。此外，从三系变换到i、i+1系变换过于突兀，极其不易理解。
因此在刷完B站能找到的所有关于牛顿欧拉法的视频后给出这个浅显易懂的推导。

汇总

总而言之，我们已经掌握了线速度、线角速度、角速度、角加速度的递推公式：

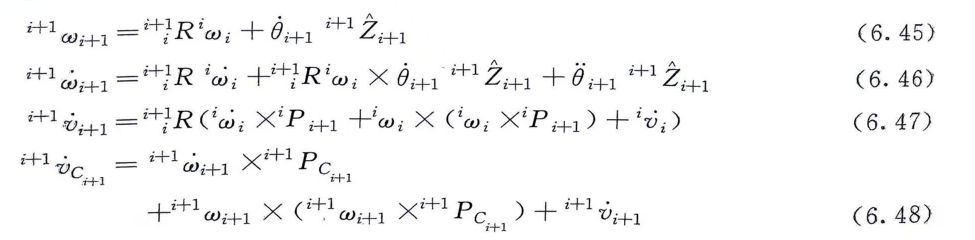
同时，牛顿和欧拉两位大佬也给我们提供了力和力矩的递推公式：

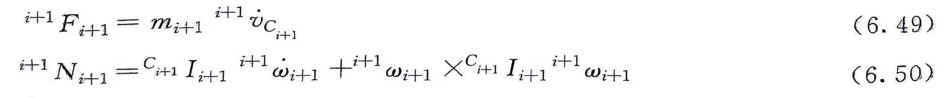
至此，我们就完成了正推公式的推导和理解，我们已经能借助前一个连杆的运动参数计算当前连杆的运动参数了。

知道运动参数后，我们就可以通过从第n连杆往回推各关节需要的力矩了。

反推

反推就是通过力、力矩和运动参数构成的方程，输入运动参数，获得各关节的力矩。

我们采用改进DH参数建模，在改进DH建模方式中，最大的区别就是第i连杆在第i关节的后面。

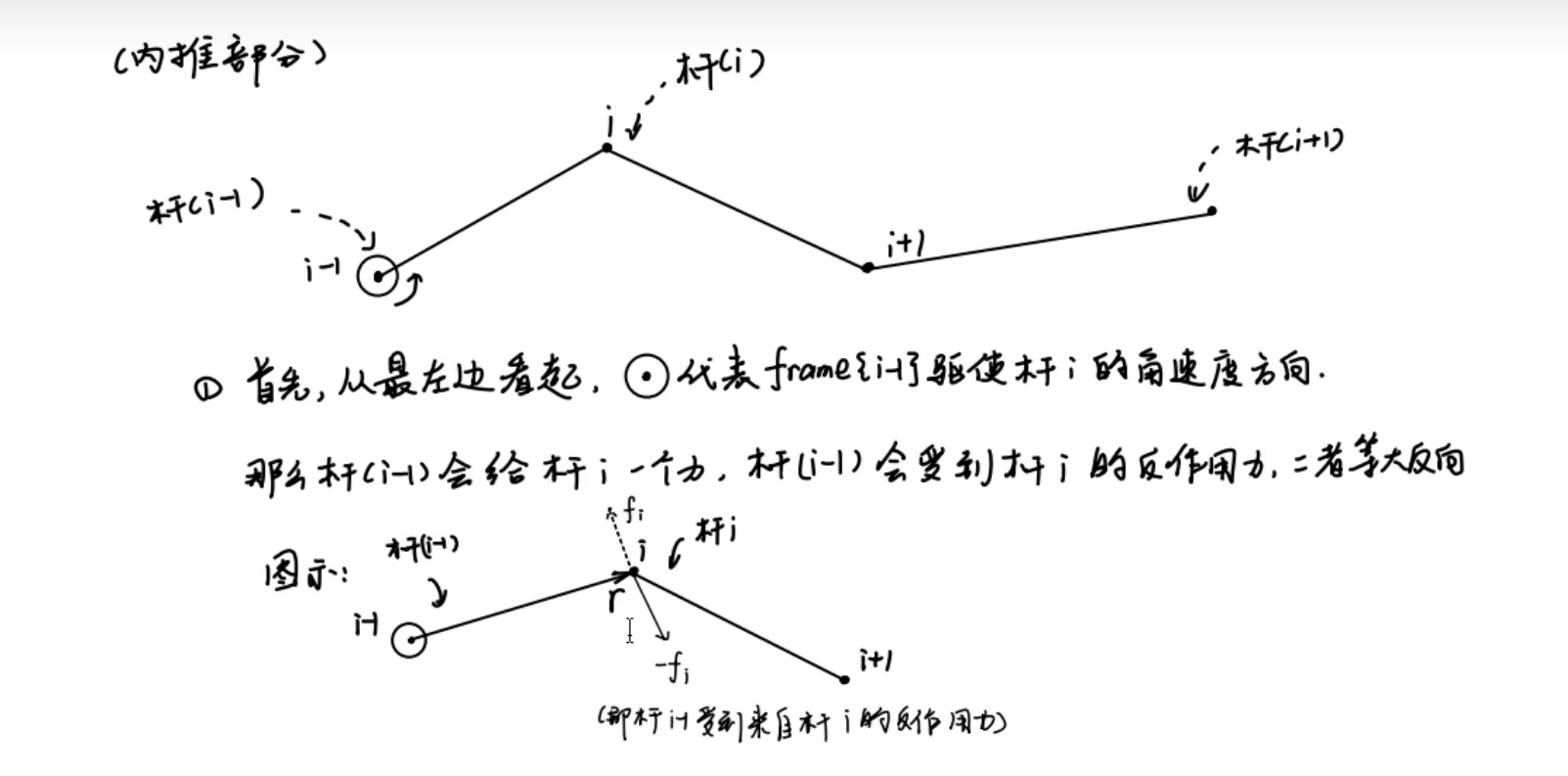
每一个关节都独立产生控制力矩，我们对第i连杆受力分析：
杆i会受到杆(i-1)的作用力 $f_i$ ，也会受到杆(i-1)的反作用力 $f_{i-1}$ 。

因此列出牛二：
$F_i = m_i \cdot \dot{v}_{c_i} = f_i - f_{i+1}$
$f_i = F_i + f_{i+1}$
其中F是该连杆质心处的合力， $f_i$ 、 $f_{i-1}$ 是作用在两侧关节的力。

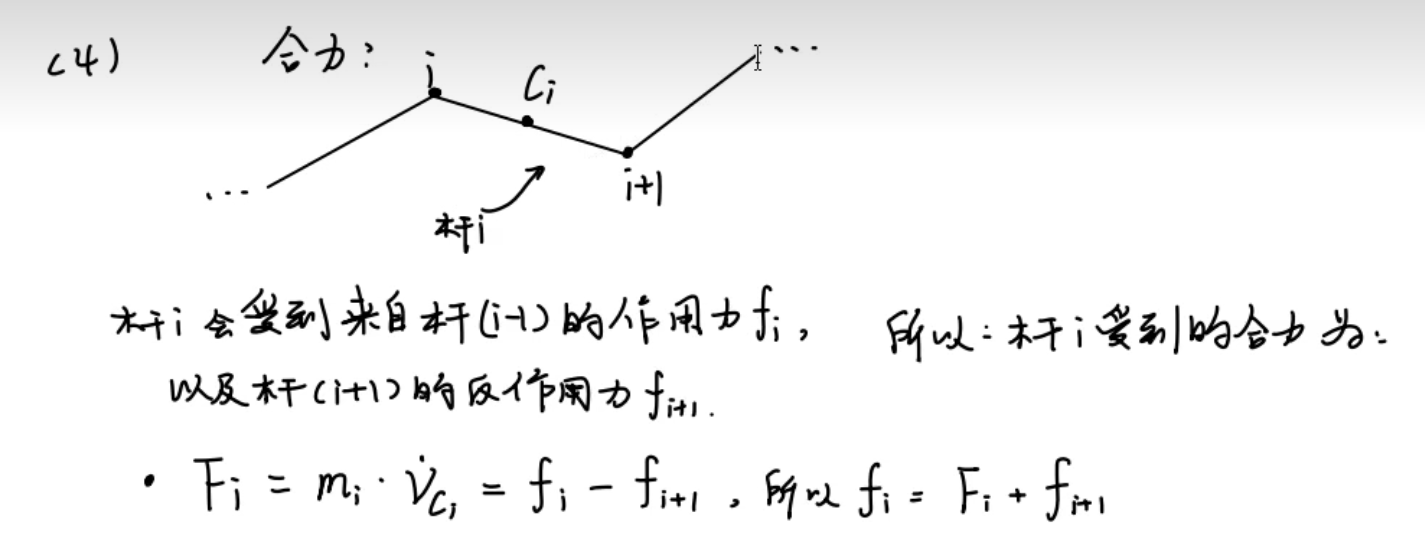
统一到{i}坐标系中：

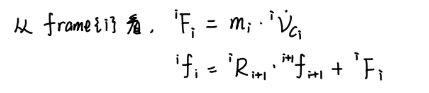
接下来，我们对连杆{i}受力分析：

假设连杆{i}存在前后两段连杆{i-1}{i+1}：
我们的目的是分析连杆{i}质心处的受力情况

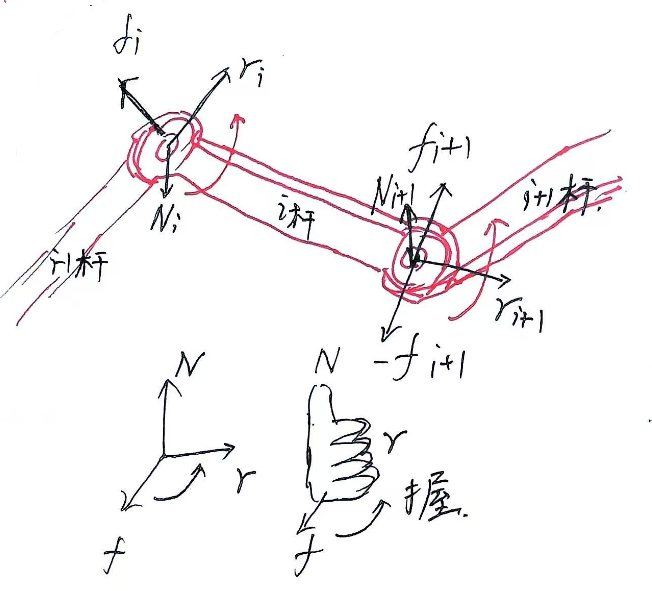
看这张抽象图：
假设所有关节的z旋转轴平行，且垂直纸面向外，这意味逆时针旋转为正向。
首先，关节{i-1}逆时针旋转，因此会给杆{i}一个向左上的力 $f_i$ 。
关节{i}也逆时针旋转，因此会给杆{i}一个向右上的力 $f_{i+1}$ ，自身会受到杆{i+1}的反作用力 $-f_{i+1}$ 。
杆{i-1}对杆{i}施加 fi 的力，力臂为r1，那么根据右手法则，四指由f指向r，得到力矩N的方向朝下（纸内）；
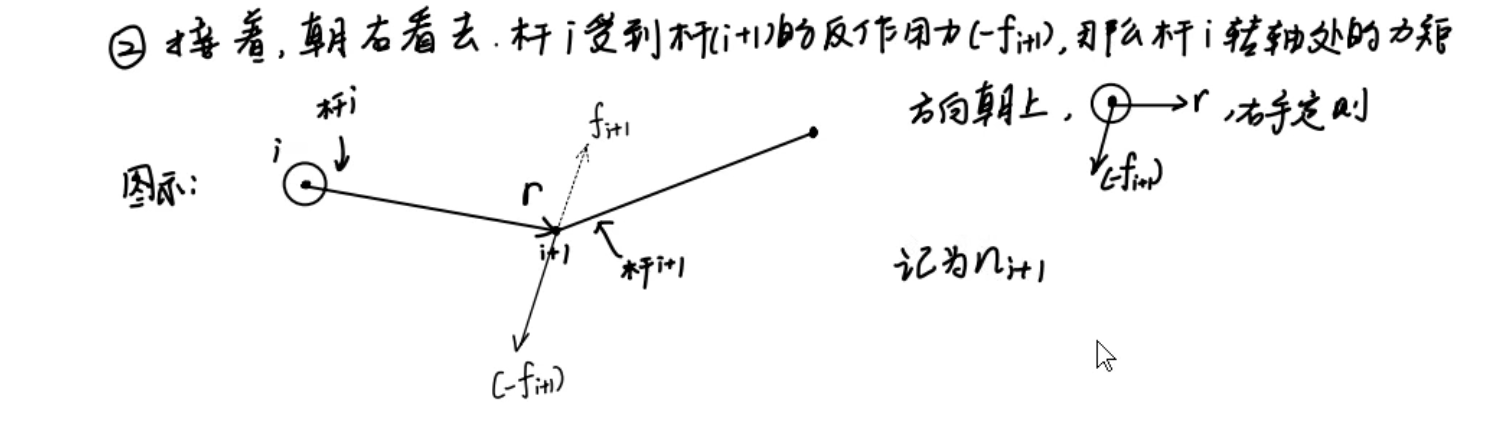
杆{i}对杆{i+1}施加 f1+1的力，力臂为ri+1，那么杆{i+1}同样会施加给它一个反作用力-fi+1，于是四指由f指向r，得到力矩N的方向朝上（纸外）；

我们的目标是要计算质心处和合力矩。目前已经得到两端相邻连杆对杆{i}的作用力矩了，还要将其转换到质心处：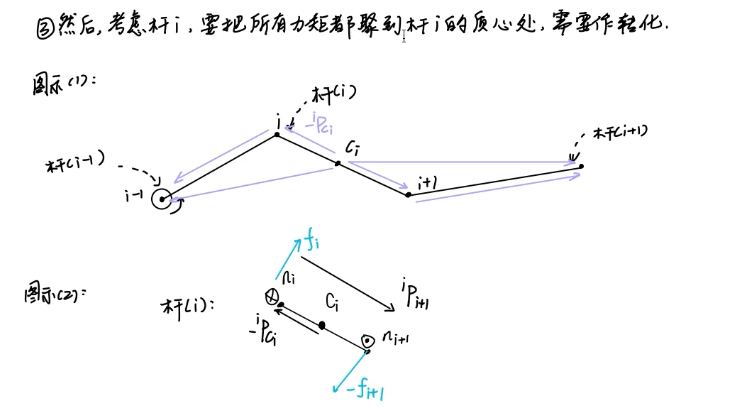

假设质心Ci向杆{i}坐标系原点的向量是 $-_{}^{i}\textrm{P}_{C_i}$ ，那么质心Ci向杆{i+1}坐标系原点的向量就是 $_{}^{i}\textrm{P}_{i+1}-_{}^{i}\textrm{P}_{C_i}$ 。
对于作用于两端的力矩就可以通过这个公式合成到质心处：得到 $_{}^{i}\textrm{N}_{i}$ 就是质心处的合力矩。

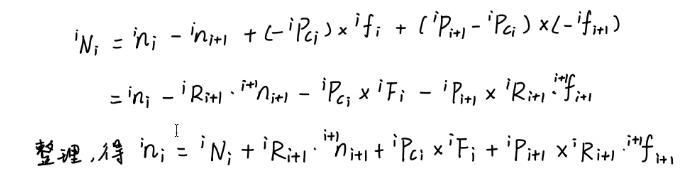
那么关节i应该施加的力可以通过移项得到 $_{}^{i}\textrm{n}_{i}$ ，观察公式，显然是和 $_{}^{i+1}\textrm{n}_{i+1}$ 相关的，因此，要计算前一个关节的力矩，就必须得知后一个关节的力矩。

这就是为什么计算力矩的过程叫做“逆推”！

而至于为什么要引入质心，就是为了构建上面的等式，构建前后关节的力矩关系，从而递推，他就是个中间变量。

我们继续，

实际上， $_{}^{i}\textrm{n}_{i}$ 并不是最终的关节力矩，而是中间计算过程中的一个变量——惯性力矩。

那它和真正的“关节力矩”是什么关系呢？

惯性力矩考虑了当前杆件和相邻杆件的惯性力矩、外力和重力的影响。
但是，我们的关节只能产生绕z轴旋转的力，至于重力或负载给的压力，它根本无法影响，换句话说，重力、压力、等非绕z轴的力无法被关节控制。

因此我们还需要提取与绕Z轴相关的力矩，这很简单，直接用Z轴的方向向量点积即可提取出这个方向上作用的力：

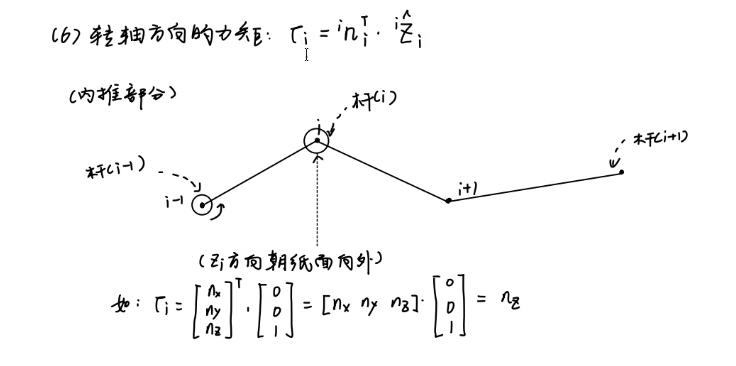
如图， $_{}^{i}\textrm{n}_{i}$ 是一个考虑了xyz三个方向和合力矩，但我们只想要z轴方向的力矩，因此乘以了 $[0,0,1]^T$ 。

至此为止，你就完全掌握了正逆推的过程！！！

我们快速总结一下：

动力学的目的就是计算在某个运动状态下，各个关节应该施加多大的力，因此核心是构建一个“运动状态-力学参数”的方程，牛顿和欧拉两位大佬就提供了。
我们的核心就变成了如何得到各个关节的“真实速度”。
我们已知各个关节的关节空间的速度、角速度、加速度，如何将前一个坐标系的运动参数传递给下一个坐标系计算呢？
这就用到了正推，构建线速度、线加速度、角速度、角加速度以及质心和端点的速度关系。
这里面最难理解的就是对Zi轴的求导，我们把求导拆成先微分再对时间求导，并用红蓝绿坐标系表示了这个过程。
最终得到了运动参数的递推公式。
我们又知道，力的传播是从末端向基座的，因此力的计算就是逆推的过程。
我们先对连杆的相互作用点进行了受力分析，并构建了端点到质心的变换公式，得以计算质心处的合力矩情况。
此时的合力矩指的是xyz三方向的合力矩，但是关节电机只能控制绕z轴旋转的力矩，因此我们将合力矩中的Z方向力矩提取出来，直接用Z的方向向量点积即可。
由此，我们就能通过得知各个关节的关节速度、加速度，从而推导出各个关节需要多大的力矩了！

听懂没？没听懂来705找我，听懂了给自己呱唧呱唧！！！

静力学分析

特别地，当机械臂的速度加速度均为零时，也就是静止时，上面的式子可以得到简化：
下式就刻画了静止时各关节力和力矩的计算方式，它可以分析静态下机械臂的负载能力。
（这一节反而在第五章P108页）

这就是Matlab机器人工具箱的rne的实现逻辑。

为什么选择牛顿欧拉法？

时间复杂度最低——仅O(n)

相对而言，拉格朗日法接近O(n^3)

方法	原理	计算效率
牛顿-欧拉法	牛顿第二定律 + 欧拉方程	⭐⭐⭐⭐⭐ O(n)
拉格朗日法	能量法	⭐⭐ O(n³)
高斯法	最小约束原理	⭐⭐
凯恩法	广义达朗贝尔原理	⭐⭐⭐