11 神经网络研究的一些问题

我们用“例子 + 公式”来分析神经网络研究中的几个问题。

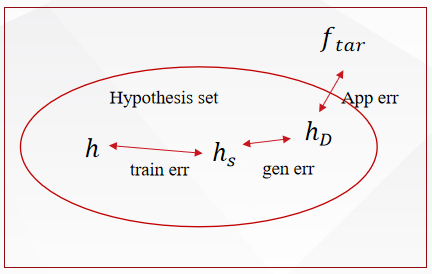
1 误差分析：模型为啥会“错”？错在哪？

就像考试，你考砸了，得搞清楚是：

• 复习没到位？（模型能力不够）
• 考试紧张发挥失常？（训练不够好）
• 平时练习题和考试题不一样？（数据不匹配）

在机器学习中，总误差可以拆成三部分：

1.1 训练误差（Training Error）

“平时做练习题的正确率”

这是模型在训练数据上的表现。比如你给模型看了100张猫狗图，它认错了5张。

公式：
$$\text{Training Error}=\frac{1}{n_{\text{train}}}\sum _{i=1}^{n_{\text{train}}}\mathcal{L}(f_{\theta }(x_i),y_i)$$
其中 $ f_\theta(x_i) $ 是模型预测，$ y_i $ 是真实标签，$ \mathcal{L} $ 是损失函数（如MSE或交叉熵）。

📌 大白话：训练误差越小，说明模型“背题”背得越好。

---

1.2 近似误差（Approximation Error）

“这个学生最聪明也只能考90分”

指最优可能的模型和真实规律之间的差距。

比如真实关系是 $y=\sin (x)$，但你非要用一条直线去拟合，那再怎么调参数也达不到完美。

公式：
$$\text{Approximation Error}=\underset{f\in \mathcal{F}}{\min }{\mathbb{E}}_{(x,y)}[\mathcal{L}(f(x),y)]$$
其中 $\mathcal{F}$ 是你允许的模型集合（比如所有神经网络）。

📌 大白话：如果你的模型家族太弱（比如只允许线性模型），那天花板就低。多层神经网络的厉害之处在于——只要层数够深，它能逼近任何连续函数（这就是著名的“通用逼近定理”）。

✅ 所以：多层网络 → 模型家族更强 → 近似误差更小

---

1.3 泛化误差（Generalization Error）

“平时练习考得好，高考也能考得好吗？”

指模型在没见过的数据上的表现。这才是真正衡量模型好坏的标准。

公式：
$$\text{Generalization Error}={\mathbb{E}}_{(x,y)}[\mathcal{L}(f_{\theta }(x),y)]$$
期望是对真实数据分布取的，但我们只能用测试集来估计它。

📌 大白话：如果训练误差很低，但测试误差很高，那就是“过拟合”——模型死记硬背了训练题，不会举一反三。

🎯 我们的目标是：最小化泛化误差，而不仅仅是训练误差。

---

2 多层网络的优势：为什么“深”比“浅”好？

例子：识别一只猫

• 单层网络：像一个“全能但笨”的人，试图用一条规则判断：“如果颜色是橘色且有胡须，就是猫”。但黑猫怎么办？
• 多层网络：像一个团队协作：
  • 第一层：检测边缘、颜色块
  • 第二层：组合成眼睛、耳朵
  • 第三层：组合成“脸”
  • 最后一层：判断是不是猫

这就是“逐层抽象”。

数学解释：非线性叠加

单层网络（线性）：
$$f(x)=Wx+b$$
只能学线性关系。

两层网络（带激活函数）：
$$h=\sigma (W^{(1)}x+b^{(1)})$$
$$f(x)=W^{(2)}h+b^{(2)}$$
其中 $\sigma$ 是非线性激活函数，比如 ReLU：$\sigma (z)=\max (0,z)$

📌 关键：没有激活函数，再多层也是线性的。
有了非线性，深层网络就能拟合极其复杂的函数。

✅ 优势总结：

• 更少的参数实现更强的表达能力（相比浅而宽的网络）
• 自动学习层次化特征（从边缘→部件→整体）
• 更容易优化（实践中深层往往比浅层表现更好）

---

3 高维问题：如何克服“维度灾难”？

3.1 什么是维度灾难？

想象你在找东西：

• 在一维（一条线）上找：容易。
• 在二维（一个房间）里找：难一点。
• 在高维空间（比如一张图片的所有像素）里找：几乎不可能！

因为随着维度增加，数据变得非常稀疏，距离失去意义，这就是“维度灾难”。

3.2 线性插值的例子

假设我们要近似一个函数 $f^{\ast }$，但不知道它的具体形式，只能通过一些点来估计它。我们可以用这些点做线性插值，就像把点连成直线一样。

一维情况

假设我们在 $[0,1]$ 区间上均匀取了 $n+1$ 个点$x_0,x_1,\dots ,x_n$，每个点之间的距离是 $h=\frac{1}{n}$。然后我们在这 $n+1$ 个点上知道函数的值 $f^{\ast }(x_j)$，并用这些点做线性插值得到$f_{\theta }(x)$。

根据泰勒展开，我们知道在任意两点之间 $x\in [x_{j-1},x_j]$，插值函数和真实函数之间的误差可以表示为：

$$f_{\theta }(x)-f^{\ast }(x)=\frac{1}{2}(x-x_{j-1})(x_j-x)f^{\prime \prime }(\tilde{x})$$

其中$\tilde{x}$ 是某个介于 $x_{j-1}$ 和 $x_j$ 之间的点。这个误差取决于二阶导数$f^{\prime \prime }(\tilde{x})$ 的大小。

由于 $(x-x_{j-1})(x_j-x)$最大不超过 $\frac{h^2}{4}$，所以误差的最大值为：

$$|f_{\theta }(x)-f^{\ast }(x)|\le \frac{h^2}{8}||f^{\prime \prime }|{|}_{\infty }=\frac{n^{-2}}{8}||f^{\prime \prime }|{|}_{\infty }$$

这里的$||f^{\prime \prime }|{|}_{\infty }$ 表示 $f^{\prime \prime }$ 在 $[0,1]$ 区间上的最大绝对值。

高维情况

当我们在更高维度 $d$ 中进行类似操作时，误差会变得更复杂，但基本思想是一样的。误差的上界变为：

$$|f_{\theta }(x)-f^{\ast }(x)|\le C_0{n}^{-\frac{1}{d}2}||D^{2}f|{|}_{\infty }$$

其中 $C_0$ 是一个常数，$D^{2}f$ 表示函数$f$ 的二阶导数矩阵（Hessian矩阵），$||D^{2}f|{|}_{\infty }$ 表示这个矩阵的最大绝对值。

3.3 数值积分的例子

假设我们要计算一个函数 $f(x)$ 在区间 $[0,1]$ 上的积分 $I$：

$$I={\int }_0^{1}f(x)\mathrm{d}x.$$

直接计算积分可能很复杂，所以我们用梯形法则来近似它。

梯形法则

把区间 $[0,1]$ 分成 $n$ 等份，每份长度为 $h=\frac{1}{n}$。然后在每个点$x_i=i\cdot h$ 计算函数值$f(x_i)$，并用这些点做梯形近似：

$$I_n=\frac{h}{2}(f(0)+f(1))+h\sum _{i=1}^{n-1}f(x_i).$$

这个公式的意思是：

• 第一个和最后一个梯形的一半高度分别是 $f(0)$ 和$f(1)$
• 中间的 $n-1$ 个梯形的高度是 $f(x_i)$

误差分析

虽然梯形法能近似积分，但肯定会有误差。误差的上界可以通过二阶导数 $f^{\prime \prime }$ 来估计：

$$|I-I_n|\le \frac{h^2}{8}\Vert f^{\prime \prime }{\Vert }_{\infty }=\frac{n^{-2}}{8}\Vert f^{\prime \prime }{\Vert }_{\infty }.$$

这里的 $\Vert f^{\prime \prime }{\Vert }_{\infty }$ 表示 $f^{\prime \prime }$ 在 $[0,1]$ 区间上的最大绝对值。

高维情况

当我们在更高维度 $d$中进行类似操作时，误差会变得更复杂，但基本思想是一样的。误差的上界变为：

$$|I-I_n|\le \frac{h^{2/d}}{8}\Vert f^{\prime \prime }{\Vert }_{\infty }=\frac{n^{-2/d}}{8}\Vert f^{\prime \prime }{\Vert }_{\infty }.$$

3.4 蒙特卡洛积分的例子

假设我们要计算一个函数 $f(x)$ 在 $d$ 维空间$[0,1{]}^d$ 上的积分$I$：
$$\begin{array}{r}I={\int }_{[0,1{]}^d}f(x)\mathrm{d}x.\end{array}$$

直接计算积分可能很复杂，所以我们用蒙特卡洛方法来近似它。

蒙特卡洛方法

我们在 $[0,1{]}^d$ 区域内随机取 $n$个点$x_1,x_2,\dots ,x_n$，然后计算这些点上的函数值 $f(x_i)$，并取平均值作为积分的近似：
$$\begin{array}{rl}I& ={\int }_{[0,1{]}^d}f(x)\mathrm{d}x\\ & \approx \frac{1}{n}\sum _{i=1}^{n}f(x_i)\end{array}$$

这个公式的意思是：

• 随机取 $n$ 个点
• 计算每个点上的函数值
• 取平均值作为积分的近似

误差分析

虽然蒙特卡洛方法能近似积分，但肯定会有误差。蒙特卡洛积分的误差平方期望值可以通过方差来估计：

$$\begin{array}{rl}\mathbb{E}(I-I_n{)}^2& =\frac{\text{Var}(f)}{n}\end{array}$$

误差平方的期望值为：

$$\begin{array}{rl}\mathbb{E}(I-I_n{)}^2& =\mathbb{E}\left(I-\frac{1}{n}\sum _{i=1}^{n}f(x_i)\right)\left(I-\frac{1}{n}\sum _{i=1}^{n}f(x_i)\right)\\ & =\mathbb{E}\left(\frac{1}{n}\sum _{i=1}^n(I-f(x_i))\cdot \frac{1}{n}\sum _{j=1}^n(I-f(x_j))\right)\\ & =\frac{1}{n^2}\sum _{i,j=1}^n\mathbb{E}(I-f(x_i))(I-f(x_j))\\ & =\frac{1}{n^2}\sum _{i=j}^n\mathbb{E}(I-f(x_i))(I-f(x_j))+\frac{1}{n^2}\sum _{i\ne j}\mathbb{E}(I-f(x_i))(I-f(x_j))\\ & =\frac{\text{Var}(f)}{n},\end{array}$$
这里的 $\frac{\text{Var}(f)}{n}$ 表示函数 $f$ 的方差除以样本数 $n$。这意味着随着样本数 $n$ 的增加，误差会减小。具体来说，误差大约是 $n^{-\frac{1}{2}}$，即样本数$n$的平方根的倒数。这个结果的一个重要特点是它与维度 $d$ 无关，也就是说，即使在高维空间中，只要增加足够的样本数，就可以有效地控制误差。

蒙特卡洛积分现在已经是一个非常成熟的领域，特别是在统计物理学中，研究人员经常需要处理非常高维的数值积分问题。由于蒙特卡洛方法的误差与维度无关，因此它在高维问题中具有很大的优势。

深度神经网络与蒙特卡洛方法的相似性

深度神经网络的结构在某些方面与蒙特卡洛方法有相似之处，尤其是在神经元数量方面。例如，一个简单的神经网络可以表示为：

$$f_{\theta }(x)=\frac{1}{m}\sum _{j=1}^m{a}_j\sigma (w_j\cdot x+b_j).$$

这里：

• $f_{\theta }(x)$ 是神经网络的输出。
• $m$ 是神经元的数量。
• $a_j$ 是每个神经元的权重。
• $\sigma$是激活函数。
• $w_j$ 和 $b_j$分别是第 $j$ 个神经元的权重向量和偏置项。
• $x$ 是输入向量。

这个公式的意思是：神经网络的输出是所有神经元输出的平均值，每个神经元的输出由其权重、偏置和激活函数决定。这种形式与蒙特卡洛方法中的随机抽样和求平均值的过程有些类似。

3.5 总结

• 维度灾难：随着维度增加，数据变得稀疏，直接处理变得困难。
• 线性插值：用已知点做线性连接来近似未知函数，误差可以通过泰勒展开来估计。
• 数值积分：用梯形法则近似积分，误差可以通过二阶导数来估计。
• 蒙特卡洛积分：用随机抽样近似积分，误差可以通过方差来估计。
• 高维插值：在高维空间中，插值误差会变得更加复杂，但基本原理相同。

3.6 神经网络怎么应对？

1. 结构归纳偏置（Inductive Bias）

   • CNN 假设“局部相关”：猫耳朵的像素是挨着的。
   • 所以用卷积核滑动检测局部模式，而不是全连接。

2. 自动降维
   网络把高维输入（如100万像素）压缩成低维“语义特征”（如100维向量表示“猫”）。

3. 稀疏激活
   比如 ReLU：很多神经元输出为0，只有少数“兴奋”，相当于只关注关键信息。

📌 大白话：神经网络不是在高维空间里“瞎撞”，而是聪明地聚焦重点区域，就像人眼不会看每个像素，而是看“轮廓”和“关键部位”。

---

4 参数那么多，为啥还能找到好解？

一个大型神经网络可能有上亿个参数。搜索空间巨大，按理说很难找到好解。但实践中，优化算法（如SGD）往往能找到不错的解。为什么？

4.1 损失函数的“地形”特性

传统认为：损失函数像“崇山峻岭”，到处是坑（局部最优）。

但研究发现：在高维空间中，大部分临界点是鞍点（saddle points），而不是局部最优。

• 局部最优：所有方向都上升
• 鞍点：有些方向上升，有些下降

SGD 的噪声可以帮助跳出鞍点。

4.2 平坦最小值（Flat Minima）泛化更好

SGD 倾向于收敛到“平坦”的最小值区域，这些区域对参数扰动不敏感，泛化性能更好。

4.3 过参数化（Over-parameterization）反而有利

当参数数量远大于样本数时：

• 解空间很大，容易找到训练误差为0的解
• 多个解中，SGD 会隐式地选择“简单”的解（类似正则化）

4.4 优化算法的智慧

• SGD（随机梯度下降）：每次只用一个样本更新，引入噪声，帮助探索。
• Adam：自适应调整每个参数的学习率，快慢结合。

📌 大白话：虽然解空间巨大，但：

• 好解其实不少（不是孤岛）
• SGD 像“盲人下山”，靠随机性和动量，大概率能找到不错的山谷
• 网络结构和数据本身提供了“路标”

---

总结：一张表看懂

问题	大白话解释	关键点
训练误差	平时练习得分	越小越好，但不能只看它
近似误差	学生的智商上限	深网络 → 上限更高
泛化误差	高考成绩	我们真正关心的
多层优势	团队协作 vs 单打独斗	逐层抽象，表达能力强
高维问题	在宇宙中找一颗星	用结构+降维聚焦重点
大量参数	在大海里捞好鱼	好解多，SGD 能游到

---

神经网络的成功，不是靠“暴力搜索”，而是结构设计 + 数据特性 + 优化算法的巧妙结合。理解这些，你就抓住了深度学习的核心逻辑。