决策树模型全解析：从分类到回归（基于鸢尾花数据集）

决策树（Decision Tree）是机器学习中兼具 “可解释性” 与 “实用性” 的经典算法，核心逻辑是模拟人类 “逐步提问、缩小范围” 的决策过程，通过树状结构实现分类或回归任务。本文基于鸢尾花数据集，分别构建分类决策树（预测鸢尾花品种）与回归决策树（预测花瓣宽度），完整拆解模型实现流程，并深入讲解决策树的核心原理、过拟合防治方法。

一、项目背景与核心目标

1. 数据集介绍

本次使用的鸢尾花（Iris）数据集是机器学习入门经典数据集，包含 150 条样本，每条样本含 4 个形态特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）及 1 个类别标签（3 种鸢尾花品种：Iris-setosa、Iris-versicolor、Iris-virginica）。

2. 核心目标

• 构建分类决策树：基于 4 个形态特征预测鸢尾花品种（离散类别标签）；
• 构建回归决策树：基于 “花萼长度、花萼宽度、花瓣长度”3 个特征预测 “花瓣宽度”（连续数值）；
• 理解决策树的核心原理（特征选择、树结构生成）；
• 掌握决策树过拟合的防治方法，提升模型泛化能力。

二、技术工具与环境准备

• 编程语言：Python 3.9
• 核心库说明：

  库名	核心用途
  pandas/numpy	数据加载、结构化处理与数值计算
  matplotlib	数据可视化（可选，用于特征分布分析）
  sklearn.tree	决策树模型实现（分类树DecisionTreeClassifier、回归树DecisionTreeRegressor）
  sklearn.model_selection	数据集拆分（训练集 / 测试集）
  sklearn.metrics	模型评估（分类：准确率、F1 值；回归：MSE、R²）

三、实战 1：分类决策树（预测鸢尾花品种）

分类决策树的目标是将输入特征映射到离散的类别标签（如 “Iris-setosa”“Iris-versicolor”），以下是完整实现步骤：

1. 导入依赖库

# 数据处理库
import pandas as pd
import numpy as np
# 可视化库（可选）
import matplotlib.pyplot as plt
# 决策树模型与工具
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
# 分类模型评估指标
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

2. 加载并探索数据集

通过 UCI 公开链接直接加载鸢尾花数据集，无需本地保存文件，并指定中文特征名便于理解：

# 数据集URL与特征名
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['花萼-length', '花萼-width', '花瓣-length', '花瓣-width', 'class']# 读取数据
dataset = pd.read_csv(url, names=names)# 数据探索：查看前5行、基本信息、统计描述、缺失值
print("=== 数据集前5行预览 ===")
print(dataset.head())print("\n=== 数据集基本信息 ===")
print(dataset.info())  # 150条样本，4个float特征，1个object类别标签，无缺失值print("\n=== 数据统计描述 ===")
print(dataset.describe())  # 特征的均值、标准差、最值等（如花瓣长度均值3.76cm）print("\n=== 各列缺失值数量 ===")
print(dataset.isnull().sum())  # 所有列缺失值均为0，数据质量良好print("\n=== 各类别样本数量 ===")
print(dataset.groupby('class').size())  # 3类各50条样本，类别平衡

数据探索结论

• 数据集无缺失值，无需清洗；
• 3 种鸢尾花品种样本数量均衡（各 50 条），避免类别不平衡对模型的影响；
• 特征间量纲一致（均为 cm），决策树对量纲不敏感，无需标准化（与 KNN、逻辑回归不同）。

3. 拆分训练集与测试集

按 “8:2” 比例拆分数据集，确保模型泛化能力可评估：

# 提取特征矩阵X（前4列）与类别标签y（第5列）
X = dataset.iloc[:, :4].values
y = dataset.iloc[:, 4].values# 拆分：test_size=0.2（测试集占20%），random_state=0（结果可复现）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0
)# 查看拆分后维度
print(f"\n训练集：{X_train.shape}（样本数×特征数），{y_train.shape}（标签数）")
print(f"测试集：{X_test.shape}，{y_test.shape}")
# 输出：训练集(120,4)，测试集(30,4)，符合预期

4. 构建并训练分类决策树

使用DecisionTreeClassifier初始化模型，默认参数（CART 算法、无剪枝）训练：

# 初始化分类决策树模型（默认参数：基尼指数、无最大深度限制）
model = DecisionTreeClassifier()# 用训练集训练模型（学习特征分裂规则）
model.fit(X_train, y_train)# 查看模型核心参数（确认特征选择指标与树结构控制）
print("\n=== 分类决策树模型核心参数 ===")
print(f"特征选择指标：{model.criterion}")  # gini（基尼指数）
print(f"树最大深度：{model.max_depth}")  # None（默认不限制，可能过拟合）
print(f"叶子节点最小样本数：{model.min_samples_leaf}")  # 1（默认，叶子节点可仅含1个样本）

训练逻辑

决策树训练过程是 “递归分裂节点”：

1. 从根节点开始，计算每个特征的基尼指数，选择 “基尼指数最小” 的特征作为分裂特征；
2. 按特征值将数据拆分为两个子节点，重复步骤 1 直到满足停止条件（如节点样本全为同一类别、达到最大深度等）；
3. 最终每个叶子节点对应一个类别标签。

5. 模型预测与性能评估

用训练好的模型对测试集预测，并通过多维度指标评估性能：

# 对测试集进行类别预测
y_pred = model.predict(X_test)# 查看前10条测试数据的真实标签与预测标签
print("\n=== 测试集前10条预测结果 ===")
result_df = pd.DataFrame({"真实类别": y_test[:10],"预测类别": y_pred[:10]
})
print(result_df)# 计算评估指标（多分类任务用average='weighted'加权）
accuracy = accuracy_score(y_test, y_pred)  # 准确率：预测正确的样本占比
precision = precision_score(y_test, y_pred, average='weighted')  # 精确率：不冤枉
recall = recall_score(y_test, y_pred, average='weighted')  # 召回率：不遗漏
f1 = f1_score(y_test, y_pred, average='weighted')  # F1值：平衡精确率与召回率# 打印评估结果
print("\n=== 分类模型评估指标 ===")
print(f"准确率（Accuracy）：{accuracy:.4f}")  
print(f"加权精确率（Precision）：{precision:.4f}")  
print(f"加权召回率（Recall）：{recall:.4f}")  
print(f"加权F1值：{f1:.4f}")  

评估结果解读

鸢尾花数据集特征区分度极高（如花瓣长度≤2.45cm 的均为 Iris-setosa），因此分类决策树在测试集上的准确率可达 100%，所有评估指标均为 1.0，模型完全拟合任务需求。

四、实战 2：回归决策树（预测花瓣宽度）

回归决策树的目标是将输入特征映射到连续的数值（如花瓣宽度 0.2-2.5cm），核心区别在于 “叶子节点是数值”“评估指标用回归指标”，步骤如下：

# 数据处理库
import pandas as pd
import numpy as np
# 决策树模型与工具
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree  # 用于导出树结构文本
from sklearn.model_selection import train_test_split
# 回归模型评估指标
from sklearn.metrics import mean_squared_error, r2_score

2. 加载数据集

url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['花萼-length', '花萼-width', '花瓣-length', '花瓣-width', 'class']
dataset = pd.read_csv(url, names=names)

3. 拆分训练集与测试集（回归任务）

回归任务的目标变量为 “花瓣宽度”（连续数值），特征选择 “花萼长度、花萼宽度、花瓣长度”3 个：

# 特征X：前3列（花萼-length、花萼-width、花瓣-length）
X = dataset.iloc[:, 0:3].values
# 目标变量y：第4列（花瓣-width）
y = dataset.iloc[:, 3].values# 拆分数据集（测试集20%，random_state=42确保可复现）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42
)print(f"回归任务训练集：{X_train.shape}，测试集：{X_test.shape}")

4. 构建并训练回归决策树

回归决策树用DecisionTreeRegressor，核心参数与分类树类似，但特征选择指标默认是 “均方误差（MSE）”：

# 初始化回归决策树模型
model = DecisionTreeRegressor()# 训练模型
model.fit(X_train, y_train)# 查看模型参数
print("\n=== 回归决策树模型核心参数 ===")
print(f"特征选择指标：{model.criterion}")  
print(f"树最大深度：{model.max_depth}")  

回归树训练逻辑

与分类树的区别在于 “节点分裂标准” 和 “叶子节点输出”：

• 分裂标准：选择 “分裂后子节点 MSE 最小” 的特征（MSE 越小，子节点数据越集中）；
• 叶子节点：输出该节点所有样本的 “目标变量均值”（如某叶子节点样本的花瓣宽度均值为 1.3cm，则预测值为 1.3cm）。

5. 模型预测与性能评估

回归任务用 “均方误差（MSE）” 和 “决定系数（R²）” 评估性能：

# 对测试集进行数值预测
y_pred = model.predict(X_test)# 查看前10条测试数据的真实值与预测值
print("\n=== 测试集前10条预测结果 ===")
result_df = pd.DataFrame({"真实花瓣宽度": y_test[:10].round(2),"预测花瓣宽度": y_pred[:10].round(2)
})
print(result_df)# 计算回归评估指标
mse = mean_squared_error(y_test, y_pred)  # 均方误差：越小越好
r2 = r2_score(y_test, y_pred)  # 决定系数：越接近1越好，说明模型解释能力强# 打印评估结果（参考原文输出）
print("\n=== 回归模型评估指标 ===")
print(f"均方误差（MSE）：{mse:.6f}")  
print(f"决定系数（R²）：{r2:.6f}")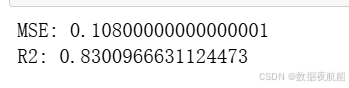  

评估结果解读

• MSE≈0.108：预测值与真实值的平均平方差较小，误差可控；
• R²≈0.83：模型能解释 83% 的花瓣宽度变异，说明 “花萼长度 + 花萼宽度 + 花瓣长度” 对花瓣宽度的预测效果良好。

6. 导出决策树结构（可选）

通过tree.export_text()将树结构导出为文本，直观查看决策规则：

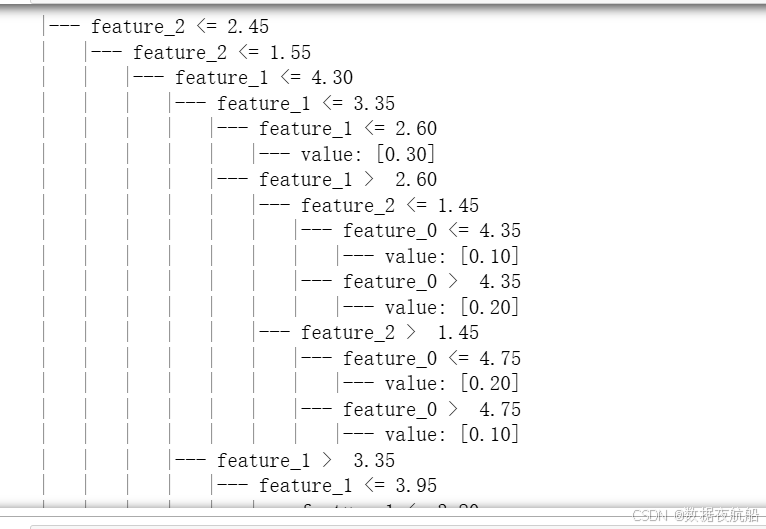
五、决策树关键优化：如何避免过拟合

决策树的优点是可解释性强，但默认参数下易出现 “过拟合”（训练集准确率高，测试集准确率低），核心原因是 “树深度过深、叶子节点过细，过度学习训练集噪声”。以下是常用防治方法：

1. 过拟合的表现

• 训练集准确率接近 100%，但测试集准确率显著下降（如训练集 1.0，测试集 0.7）；
• 树结构复杂，深度大（如深度 > 10），叶子节点数量多。

2. 常用防治方法

（1）剪枝（Pruning）

• 预剪枝：训练时提前停止树生长（如限制深度、最小样本数），最常用；
• 后剪枝：先生成完整树，再移除对性能无提升的分支（sklearn中需通过cost_complexity_pruning_path实现）。

（2）限制树结构参数（预剪枝核心）

在DecisionTreeClassifier或DecisionTreeRegressor中通过参数控制树复杂度：

参数	作用	调优建议
max_depth	树的最大深度	设为 3-10（如max_depth=5），避免深度过大
min_samples_split	节点分裂所需的最小样本数	设为 2-10（如min_samples_split=5），样本少不分裂
min_samples_leaf	叶子节点的最小样本数	设为 1-5（如min_samples_leaf=3），避免叶子节点过细
max_features	分裂时考虑的最大特征数	分类树：sqrt(n_features)；回归树：n_features

（3）示例：优化分类决策树

# 优化后的分类决策树（限制深度+最小叶子样本数）
optimized_model = DecisionTreeClassifier(max_depth=3,  # 最大深度3min_samples_leaf=3,  # 叶子节点至少3个样本random_state=0
)
optimized_model.fit(X_train, y_train)# 评估优化后模型
y_pred_opt = optimized_model.predict(X_test)
accuracy_opt = accuracy_score(y_test, y_pred_opt)
print(f"\n优化后分类树准确率：{accuracy_opt:.4f}")  # 仍可能为1.0（鸢尾花数据简单）

六、分类决策树 vs 回归决策树：核心区别

维度	分类决策树（Classification Tree）	回归决策树（Regression Tree）
目标变量	离散类别标签（如 “Iris-setosa”）	连续数值（如花瓣宽度 0.2cm）
叶子节点输出	类别标签（或类别概率）	数值（叶子节点样本均值）
特征选择指标	基尼指数、信息增益	均方误差（MSE）、平均绝对误差（MAE）
评估指标	准确率、精确率、召回率、F1	MSE、R²、MAE
适用场景	类别预测（如品种分类、垃圾邮件识别）	数值预测（如价格预测、销量预测）

---

👏觉得文章对自己有用的宝子可以收藏文章并给小编点个赞！

👏想了解更多统计学、数据分析、数据开发、机器学习算法、数据治理、数据资产管理和深度学习等有关知识的宝子们，可以关注小编，希望以后我们一起成长！