算法 --- 字符串
字符串
字符串算法题目主要处理文本的查找、匹配、比较、变换和统计问题,其核心特点是输入数据为字符序列,解题关键在于利用其连续性、前缀性、字典序等特性,并常借助哈希、自动机、指针滑动、动态规划等技巧高效处理。
详细分类型与适用场景
当一道题的输入是一个或多个字符串时,你就应该考虑使用字符串算法。以下是主要的题目类型和适用场景:
1. 基础操作与模拟
-
特点:直接考察对字符串的索引、遍历、拼接、反转等基本操作。
-
常见题型:字符串反转、判断回文串、实现基本的字符串转换(如
atoi)、Z字形变换等。 -
适用场景:问题描述本身就像是在指导你一步步操作字符串。
2. 匹配与查找问题
这是字符串问题的核心领域。
-
特点:在一个主串(文本)中查找一个或多个模式串是否存在及出现的位置。
-
常见算法:
-
暴力匹配:简单但低效,适用于小规模数据。
-
KMP算法:高效的单模式串匹配,利用“部分匹配表”避免回溯。
-
Rabin-Karp算法:利用滚动哈希进行多模式串匹配的预处理。
-
字典树(Trie):快速检索字符串集合中是否存在某个前缀或整个字符串。
-
AC自动机:字典树 + KMP 的思想,用于多模式串匹配的终极武器(如敏感词过滤)。
-
-
适用场景:问题中出现“查找子串”、“所有出现位置”、“是否包含某些单词”等关键词。
3. 子串与子序列问题
-
特点:不要求连续(子序列)或要求连续(子串)的序列问题,常求最大、最小、最长、最短等。
-
常见题型:
-
最长回文子串:使用中心扩散法或Manacher算法。
-
最长公共子串/子序列(LCS):经典动态规划问题。
-
最长不含重复字符的子串:使用滑动窗口(双指针)的代表性问题。
-
最短编辑距离:另一个经典的动态规划问题,衡量两个字符串的相似度。
-
-
适用场景:问题要求找到一个满足特定条件的“序列”,且这个序列源自原字符串。
4. 计数与统计问题
-
特点:统计字符串中字符、子串、模式出现的频率、数量或分布。
-
常见题型:统计字母出现次数、统计“优美子串”的数目、不同子串的个数等。
-
适用场景:问题中出现“有多少种”、“出现次数”、“频率最高”等统计性词汇。常结合哈希表来记录频率。
5. 分割与组合问题
-
特点:将字符串按一定规则进行分割,或者由多个部分组合成一个新字符串。
-
常见题型:单词拆分、回文分割、恢复IP地址等。
-
适用场景:问题要求将字符串切割成若干段,每段需要满足特定条件。这类问题通常使用回溯法(DFS) 或动态规划来解决。
6. 表达式 parsing 与计算
-
特点:处理具有特定语法结构的字符串,如数学表达式、JSON、XML等。
-
常见题型:基本计算器(实现加减乘除括号)、逆波兰表达式求值、解析HTML标签等。
-
适用场景:输入字符串具有明确的递归或嵌套结构。解决方案通常是使用栈或递归下降等解析方法。
7. 字符串排序与字典序问题
-
特点:利用字符串的字典序特性进行排序或比较。
-
常见题型:拼接所有字符串使字典序最小、最长快乐前缀、后缀数组等。
-
适用场景:问题要求比较字符串的“大小”或按特定顺序排列字符串。
总结
当你看到问题的输入是字符串,并且问题目标涉及查找、匹配、比较、变换、计数、分割这几种操作时,它就是一个字符串算法题。解决它们的关键是选择合适的数据结构(哈希表、Trie、栈)和算法思想(滑动窗口、动态规划、回溯、自动机)。
题目练习
14. 最长公共前缀 - 力扣(LeetCode)
解法:
算法思路:
解法一(两两比较):
我们可以先找出前两个的最长公共前缀,然后拿这个最长公共前缀依次与后面的字符串比较,这样就可以找出所有字符串的最长公共前缀。
class Solution {
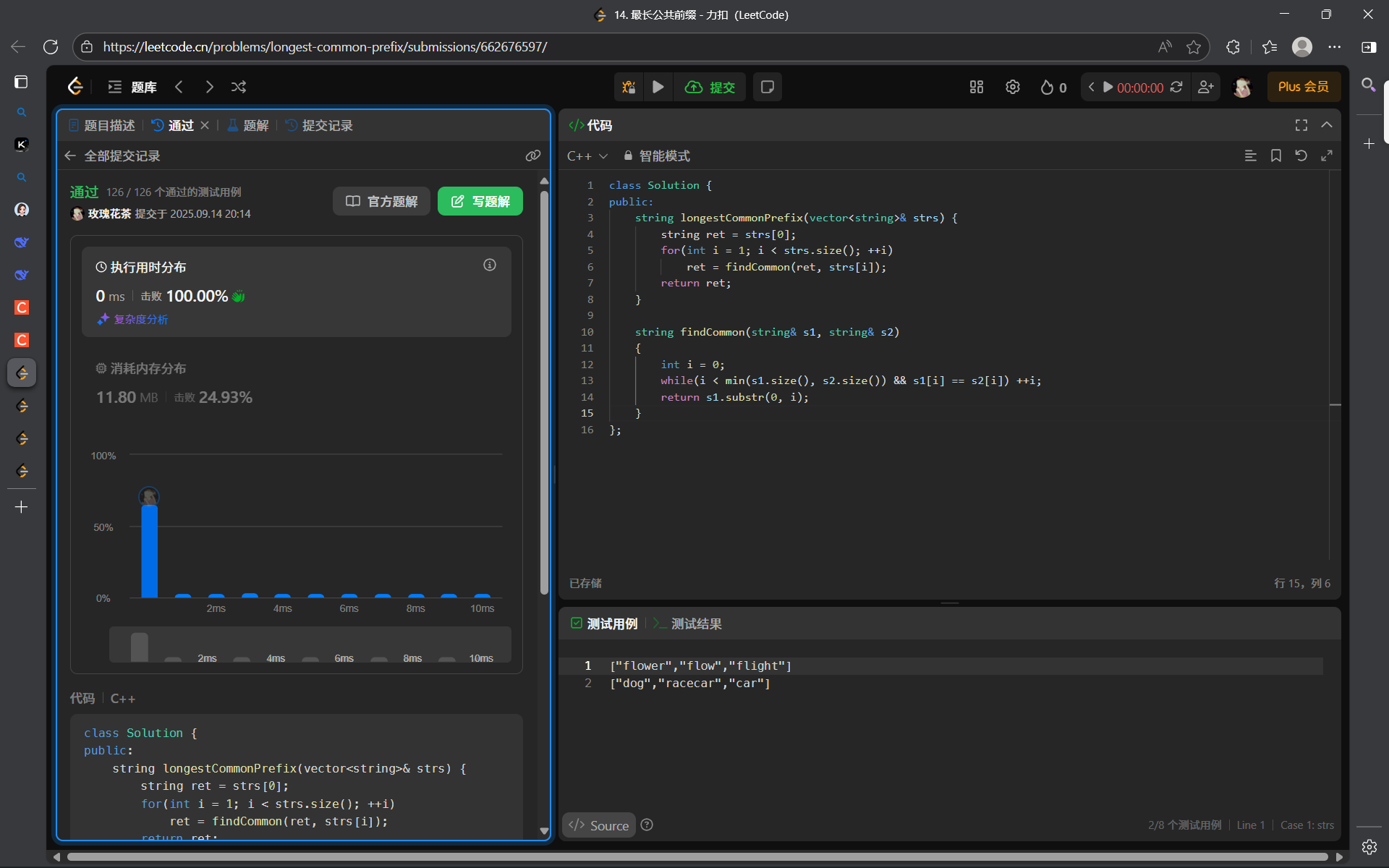
public:string longestCommonPrefix(vector<string>& strs) {string ret = strs[0];for(int i = 1; i < strs.size(); ++i)ret = findCommon(ret, strs[i]);return ret;}string findCommon(string& s1, string& s2){int i = 0;while(i < min(s1.size(), s2.size()) && s1[i] == s2[i]) ++i;return s1.substr(0, i);}
};
解法二(统一比较):
题目要求多个字符串的公共前缀,我们可以逐位比较这些字符串,哪一位出现了不同,就在哪一位截止。
class Solution {
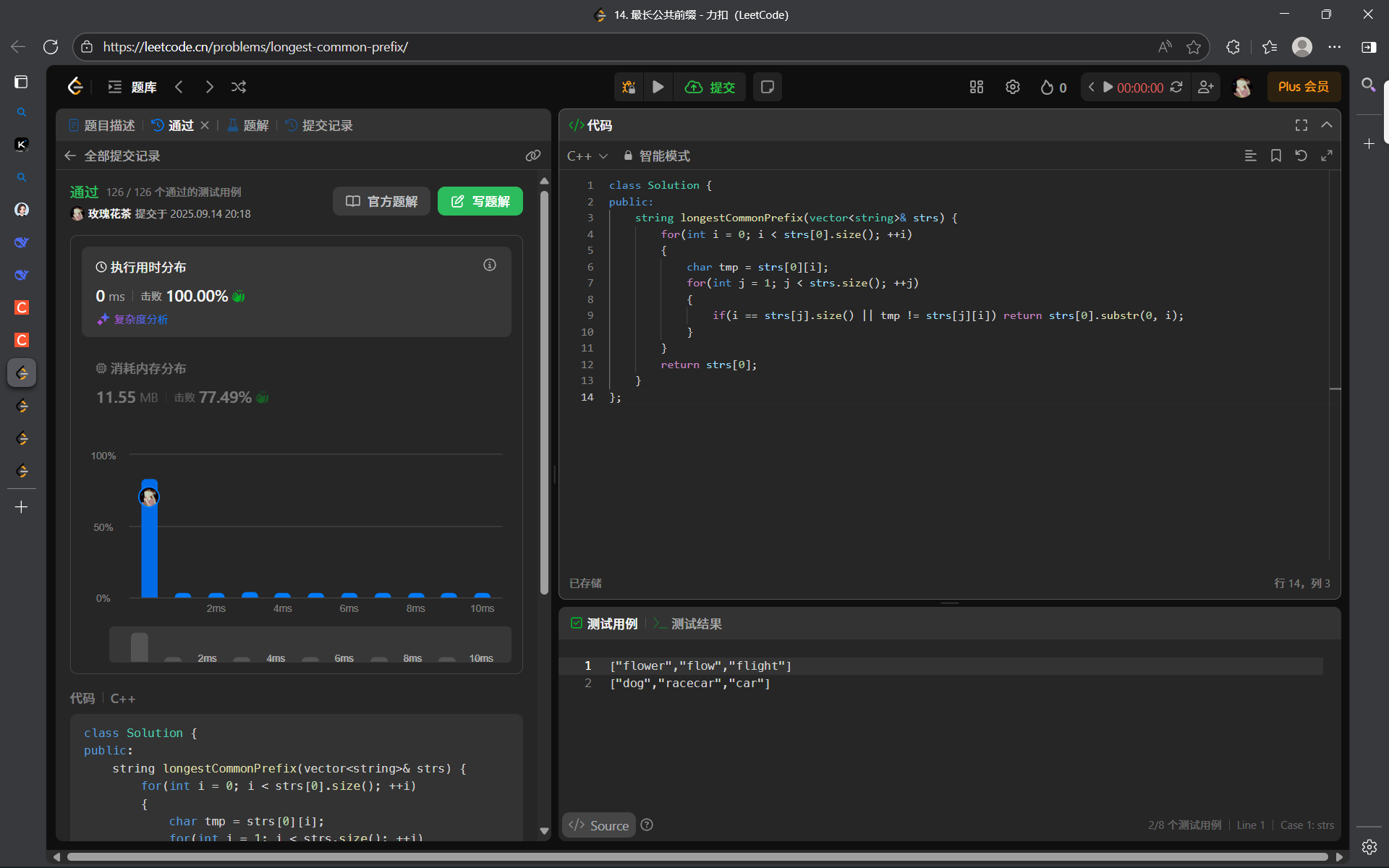
public:string longestCommonPrefix(vector<string>& strs) {for(int i = 0; i < strs[0].size(); ++i){char tmp = strs[0][i];for(int j = 1; j < strs.size(); ++j){if(i == strs[j].size() || tmp != strs[j][i]) return strs[0].substr(0, i);}}return strs[0];}
};
5. 最长回文子串 - 力扣(LeetCode)
解法(中心扩散):
算法思路:
枚举每一个可能的子串非常费时,有没有比较简单一点的方法呢?
对于一个子串而言,如果它是回文串,并且长度大于 2,那么将它首尾的两个字母去除之后,它仍然是个回文串。如此这样去除,一直除到长度小于等于 2 时呢?长度为 1 的,自身与自身就构成回文;而长度为 2 的,就要判断这两个字符是否相等了。
从这个性质可以反推出来,从回文串的中心开始,往左读和往右读也是一样的。那么,是否可以枚举回文串的中心呢?
从中心向两边扩展,如果两边的字母相同,我们就可以继续扩展;如果不同,我们就停止扩展。这样只需要一层 for 循环,我们就可以完成先前两层 for 循环的工作量。
class Solution {
public:string longestPalindrome(string s) {int begin = 0, len = 0, n = s.size();for(int i = 0; i < n; ++i){int left = i, right = i;while(left >= 0 && right < n && s[left] == s[right]){left--;right++;}if(right - left - 1 > len){begin = left + 1;len = right - left - 1;}left = i, right = i + 1;while(left >= 0 && right < n && s[left] == s[right]){left--;right++;}if(right - left - 1 > len){begin = left + 1;len = right - left - 1;}}return s.substr(begin, len);}
};
67. 二进制求和 - 力扣(LeetCode)
解法(模拟十进制的大数相加的过程):
算法思路:
模拟十进制中我们列竖式计算两个数之和的过程。但是这里是二进制的求和,我们不是逢十进一,而是逢二进一。
class Solution {
public:string addBinary(string a, string b) {string ret;int cur1 = a.size() - 1, cur2 = b.size() - 1, t = 0;while(cur1 >= 0 || cur2 >= 0 || t){if(cur1 >= 0) t += a[cur1--] - '0';if(cur2 >= 0) t += b[cur2--] - '0';ret += t % 2 + '0';t /= 2;}reverse(ret.begin(), ret.end());return ret;}
};
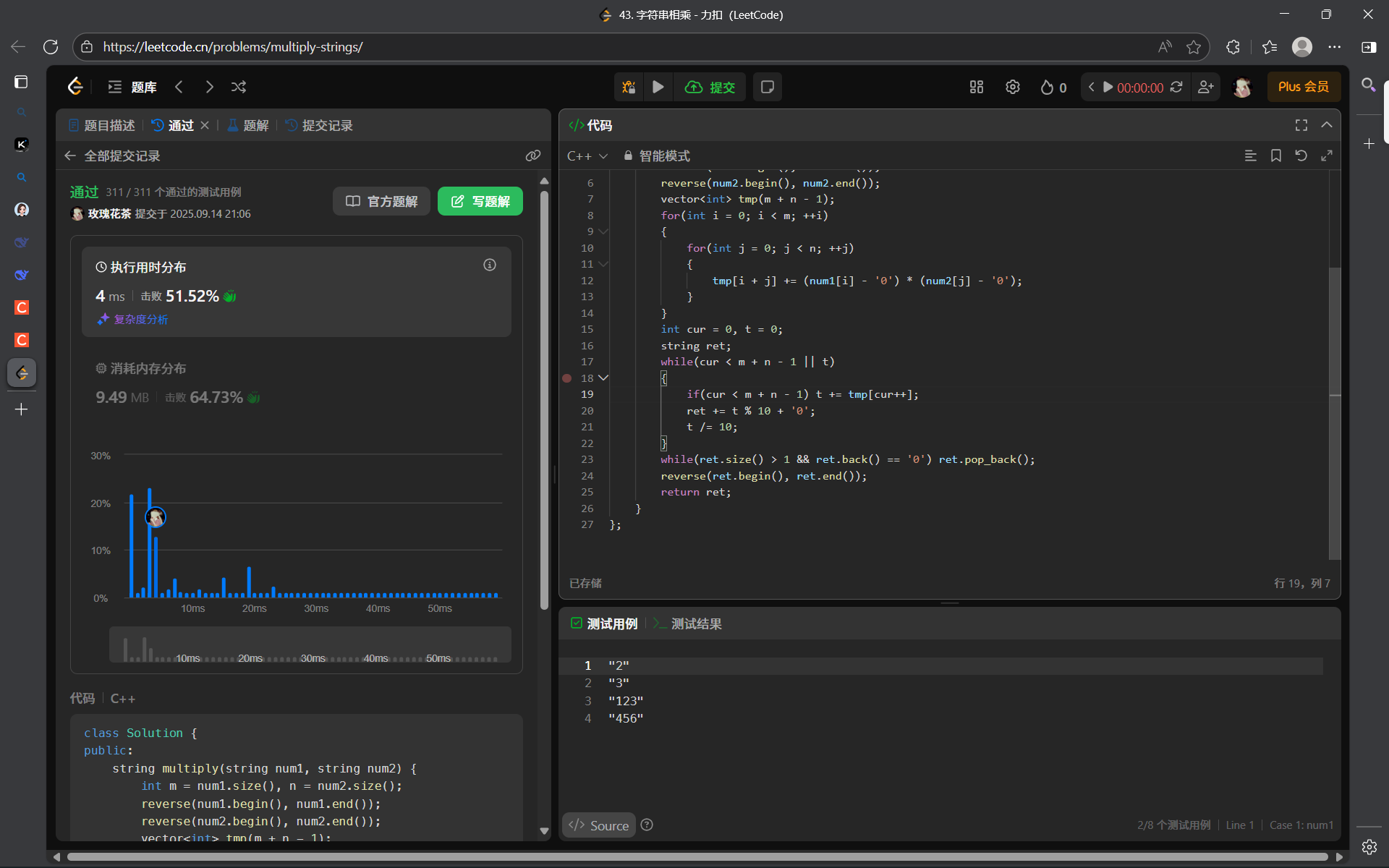
43. 字符串相乘 - 力扣(LeetCode)
解法(无进位相乘然后相加,最后处理进位):
算法思路:
整体思路就是模拟我们小学列竖式计算两个数相乘的过程。但是为了我们书写代码的方便性,我们选择一种优化版本的,就是在计算两数相乘的时候,先不考虑进位,等到所有结果计算完毕之后,再去考虑进位。如下图:

class Solution {
public:string multiply(string num1, string num2) {int m = num1.size(), n = num2.size();reverse(num1.begin(), num1.end());reverse(num2.begin(), num2.end());vector<int> tmp(m + n - 1);for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){tmp[i + j] += (num1[i] - '0') * (num2[j] - '0');}}int cur = 0, t = 0;string ret;while(cur < m + n - 1 || t){if(cur < m + n - 1) t += tmp[cur++];ret += t % 10 + '0';t /= 10;}while(ret.size() > 1 && ret.back() == '0') ret.pop_back();reverse(ret.begin(), ret.end());return ret;}
};