当前位置：首页 > news >正文

[数据结构——Lesson14.快速排序]

news 2025/9/16 7:59:58

前言

学习目标

1.分治策略（Divide and Conquer）

1.1分治策略的核心步骤

1. 分解（Divide）：拆分大问题为子问题

2. 解决（Conquer）：递归求解子问题

3.合并（Combine）：合并子问题结果

1.2分治策略的适用场景

1.3分治策略的优缺点

优点：

缺点：

2.快速排序（Quick Sort）

2.1算法思想：

2.2算法步骤

2.3方法解析

(1)Hoare法

(2)挖坑法

(3)前后指针法

3.复杂度分析

算法优化

① 改变基准值

②三指针分划区间

一、核心定义：3 个指针的初始定位

二、执行流程：cur 遍历与指针调整

三、最终结果：3 个区间的明确划分

③区间优化

非递归实现

前言

上节内容我们讲到了两个排序算法——冒泡排序和选择排序[数据结构——Lesson13.冒泡与选择排序]，这一节我们将详细讲解设计巧妙而且使用非常广泛的排序算法——快速排序。

学习目标

什么是分治策略
快速排序的掌握

1.分治策略（Divide and Conquer）

在学习快排之前，我们先了解一下什么是分治策略？

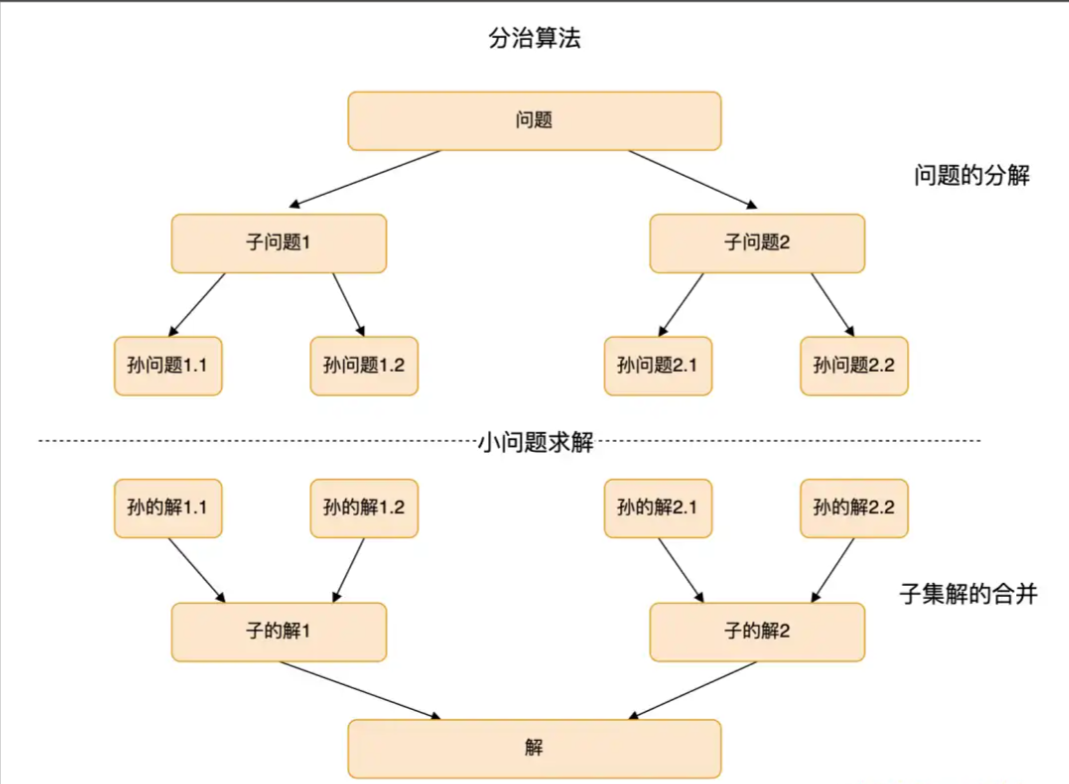
分治策略（Divide and Conquer）是一种经典的算法设计思想，核心逻辑可概括为 “分而治之”—— 将复杂的大问题拆解为多个结构相同、规模更小的子问题，通过解决子问题，最终合并子问题的结果得到原问题的解。它是高效算法（如快速排序、归并排序、二分查找等）的核心思想之一，尤其适用于解决规模庞大、直接求解困难的问题。

1.1分治策略的核心步骤

分治策略的执行过程通常分为 3 个关键阶段，且这 3 个阶段会通过递归（或迭代）重复执行，直到子问题足够简单可直接求解：

1. 分解（Divide）：拆分大问题为子问题

将原问题（规模为 n）按照某种规则拆分为 k个 规模更小、结构与原问题一致 的子问题（例如将规模 n 拆分为 2 个规模 n/2 的子问题）。

关键要求：子问题需与原问题 “同构”（即解决逻辑相同），且拆分后子问题之间 相互独立（无依赖关系，可并行求解）。
示例：对数组 [5,3,7,1,4,8,2] 用分治排序时，可拆分为 [5,3,7] 和 [1,4,8,2] 两个子数组（子问题仍是 “数组排序”，且两个子数组独立）。

2. 解决（Conquer）：递归求解子问题

递归地对每个子问题进行求解：

若子问题规模足够小（达到 “基线条件”，如子数组长度为 1），则直接得到解（单个元素默认有序，无需额外计算）；
若子问题仍较复杂，则继续重复 “分解→解决” 的过程，直到子问题满足基线条件。
示例：上述子数组 [5,3,7] 继续拆分为 [5,3] 和 [7]，其中 [7] 满足基线条件（直接有序），[5,3] 再拆分为 [5] 和 [3]（均满足基线条件）。

3.合并（Combine）：合并子问题结果

将所有子问题的解合并，得到原问题的最终解。

合并是分治策略的 “关键收尾步骤”，不同问题的合并逻辑差异较大（部分简单问题可省略合并，如快速排序）。
示例：归并排序中，需将两个有序子数组（如 [3,5] 和 [7]）合并为一个有序数组 [3,5,7]；而快速排序中，由于子问题的解（有序子区间）本身已在原数组中 “原位有序”，无需额外合并操作。

1.2分治策略的适用场景

并非所有问题都适合分治策略，需满足以下 4 个条件：

问题可拆分：原问题能拆分为多个规模更小的子问题，且子问题结构与原问题一致；
子问题独立：子问题之间无依赖，求解一个子问题时无需依赖其他子问题的中间结果；
基线条件存在：子问题规模缩小到一定程度后，可直接求解（无需继续拆分）；
结果可合并：子问题的解能通过合理逻辑合并为原问题的解。

典型应用场景：

排序算法：快速排序（拆分后无需合并）、归并排序（拆分后需合并）；
查找算法：二分查找（拆分后仅需求解一个子问题）；
数值计算：大整数乘法、矩阵乘法（Strassen 算法）；
组合问题：汉诺塔问题、逆序对计数。

1.3分治策略的优缺点

优点：

降低问题复杂度：将 “无法直接解决的大问题” 拆解为 “可轻松解决的小问题”，大幅降低求解难度；
高效利用资源：子问题独立的特性使其支持并行计算（如多线程求解不同子问题）；
时间复杂度优化：多数分治算法的时间复杂度为 O(NlogN)（如快速排序、归并排序），远优于暴力算法的 O(N²)。

缺点：

空间开销较高：递归实现的分治算法需额外的 “递归调用栈” 空间（如快速排序最坏情况空间复杂度 O(N)）；
合并逻辑复杂：部分问题的合并步骤难度高、开销大（如归并排序的合并需额外数组存储临时结果）；
不适合小规模问题：递归的函数调用 / 返回开销，可能导致分治算法在小规模问题上效率低于简单算法（如快速排序优化中，子数组长度较小时改用插入排序）。

2.快速排序（Quick Sort）

2.1算法思想：

快速排序采用分治策略，通过选择一个基准值，将待排序数据分割为两部分，使得左边部分数据都小于右边部分数据。接着分别对这两部分数据递归进行快速排序，直至整个数据有序。例如对数组 [5, 3, 7, 1, 4, 8, 2, 9, 6, 0] 排序，选择 5 作为基准值，一趟排序后数组分为 [3, 1, 4, 2, 0] 和 [7, 8, 9, 6] 两部分，再分别对这两部分递归排序，最终实现整个数组有序。

2.2算法步骤

Hoare 法：
①设定 left 和 right 指针分别指向数组首尾，选择数组首元素为基准 key；
②right 从右往左找比 key 小的数，left 从左往右找比 key 大的数，找到后交换 left 与 right 下标对应的值，重复直至 right≥left；
③之后交换 key 与 left 或 right 对应的值，记录该位置为 mid，划分数组；
④对 [left, mid - 1] 和 [mid + 1, right] 子数组重复上述过程，直至数组排序完成。

挖坑法：
①设置 left 和 right 指针分别指向数组两端，选取数组首元素为基准值 key 并设起始位置为坑；
②right 从右往左找比 key 小的值放入坑位，形成新坑，left 从左往右找比 key 大的值放入坑位，更新坑位；
③left 与 right 相遇时，将 key 放入最后一个坑，记录位置为 mid；
④划分区间 [left，mid - 1] 与 [mid + 1,right] 重复上述步骤，直至不能划分。

前后指针法：
①将数组第一个元素作为 key 基准值，定义前指针 prev 指向第一个数，后指针 cur 指向第二个数；
②cur 从左往右找比 key 小的值，找到后 ++prev，交换 prev 与 cur 指向的值，cur 继续遍历；
③cur 遍历完后，交换 prev 指向的值与 key，记录此时位置为 mid；
④划分区间 [left，mid - 1] 与 [mid + 1,right] 重复上述步骤，直至不能划分。

稍安勿躁，接下来我们一个一个介绍

2.3方法解析

(1)Hoare法

①设定 left 和 right 指针分别指向数组首尾，选择数组首元素为基准 key；
②right 从右往左找比 key 小的数，left 从左往右找比 key 大的数，找到后交换 left 与 right 下标对应的值，重复直至 right≥left；
③之后交换 key 与 left 或 right 对应的值，记录该位置为 mid，划分数组；
④对 [left, mid - 1] 和 [mid + 1, right] 子数组重复上述过程，直至数组排序完成。

下面我们来看个例子：

① 起始状态，key为数组的起始位置，left在起始位置，right在末尾。

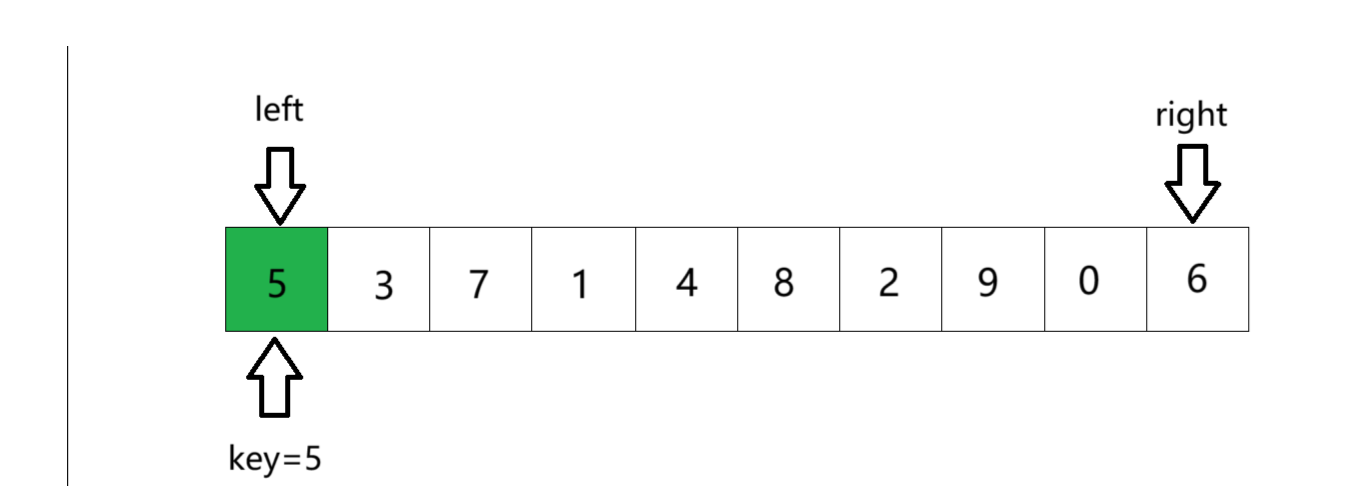
② right先出发（必须！！！），寻找比key小的数字。找到则停下。

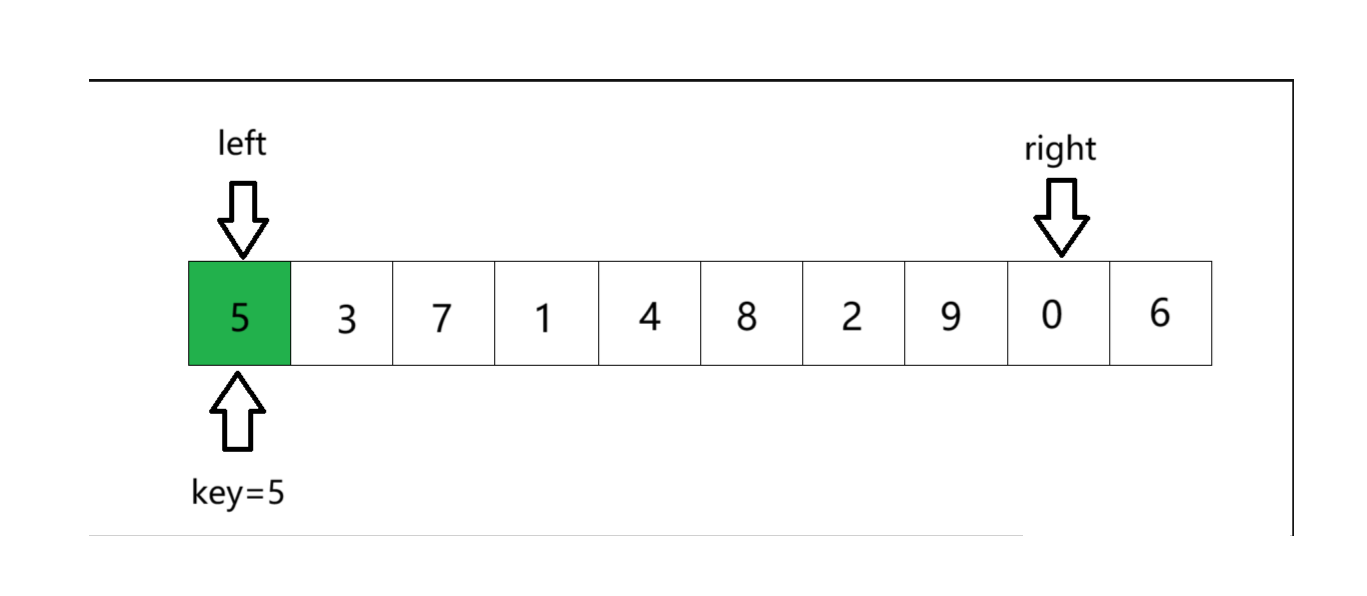
③left出发，寻找比key大的数字。找到则停下。

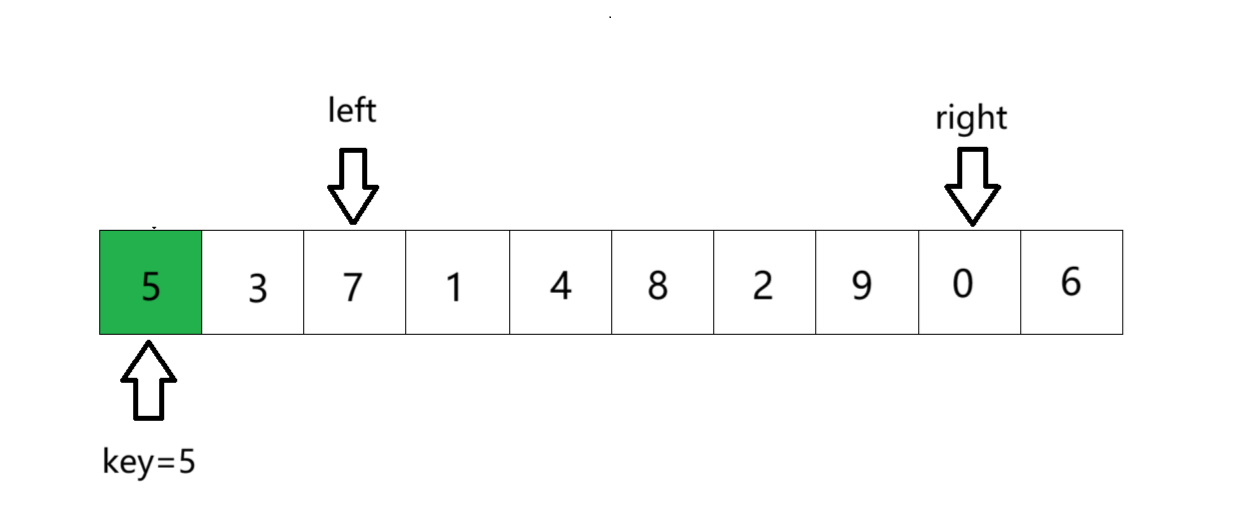
④ 交换left和right的数字。

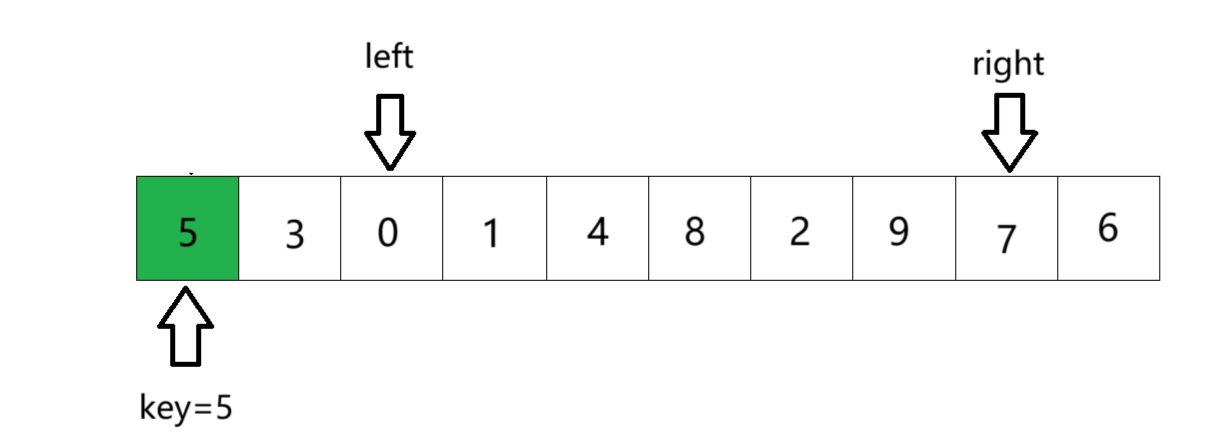
⑤ 接着走，right找比key大的数，left找比key小的数，交换。

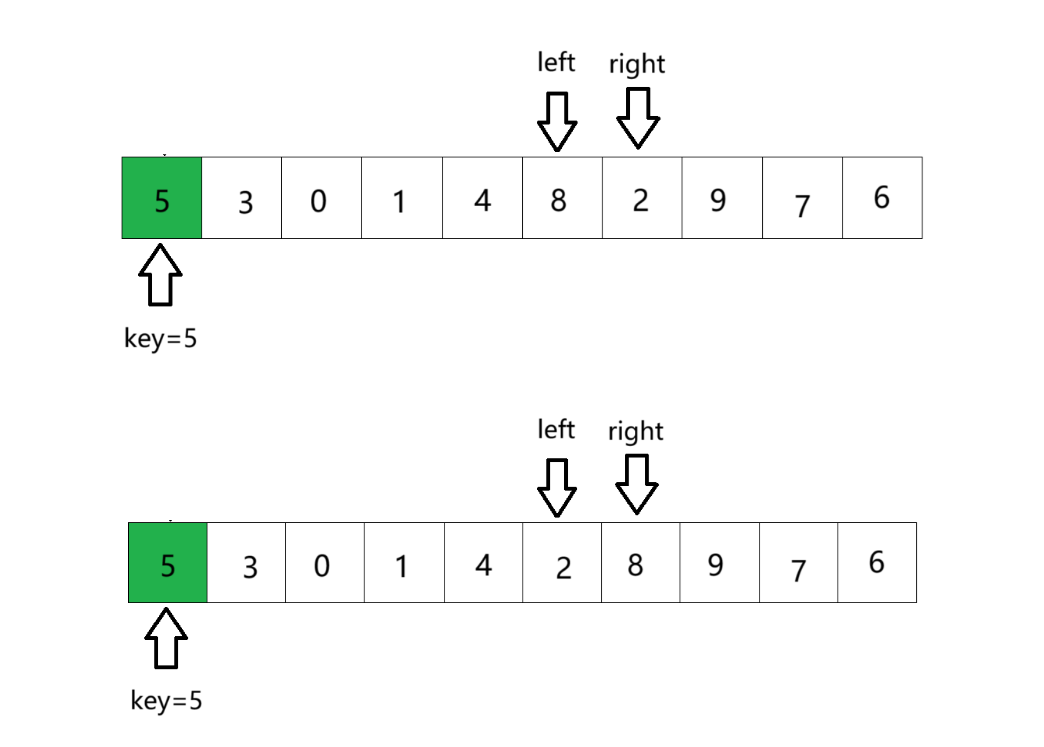
⑥ right接着走，遇到left，此时指向同一位置。

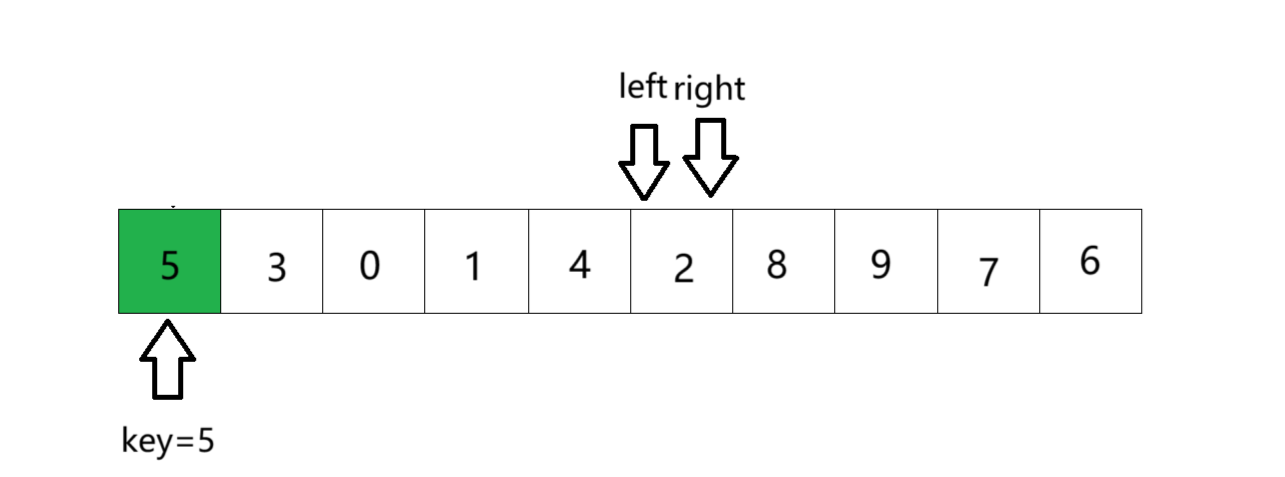
⑦ 将left与right指向的数与key进行交换，则单趟排序就完成了，最后将基准值的下标返回给函数调用者

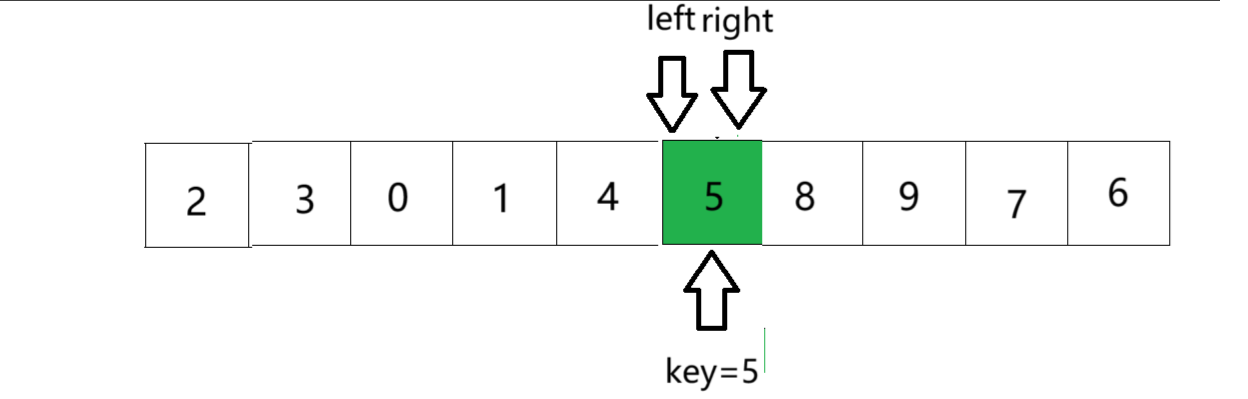
动图演示：

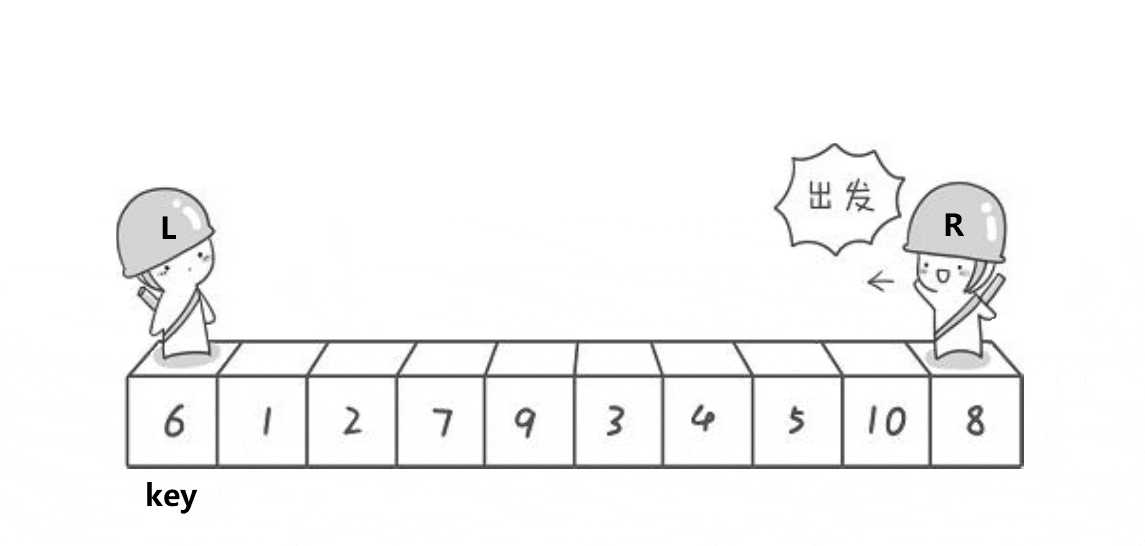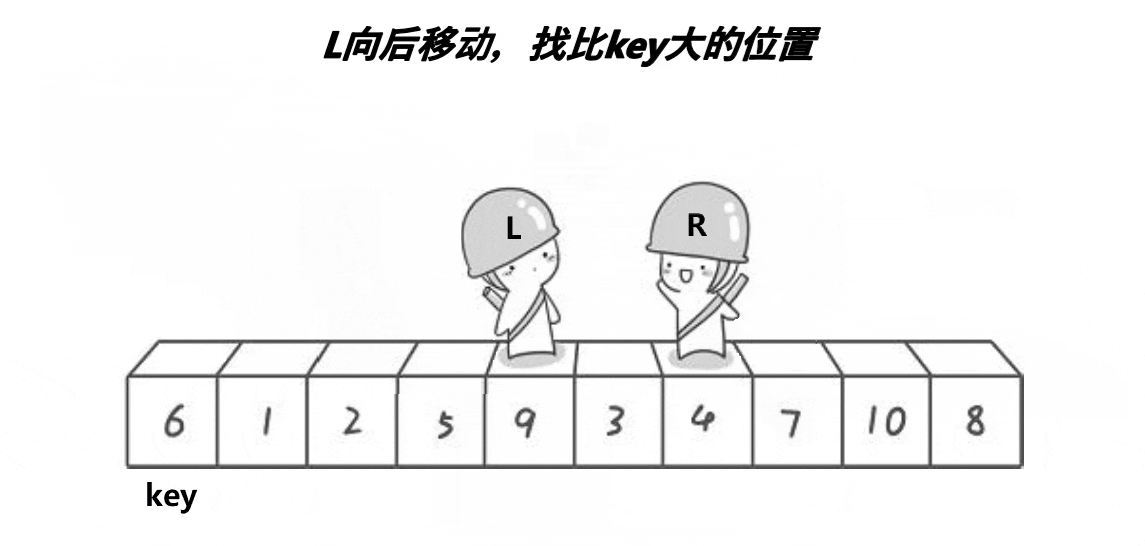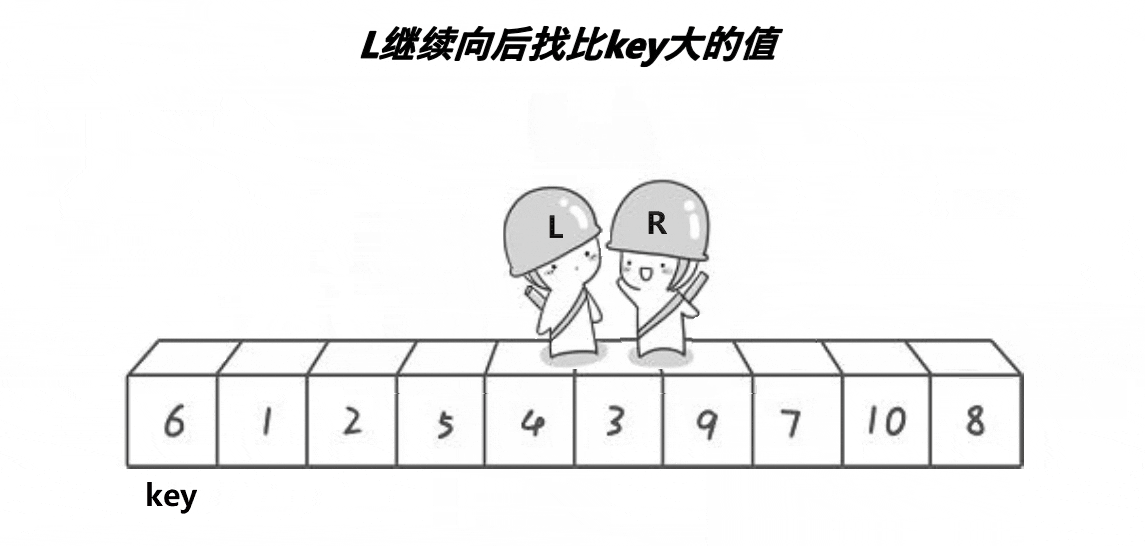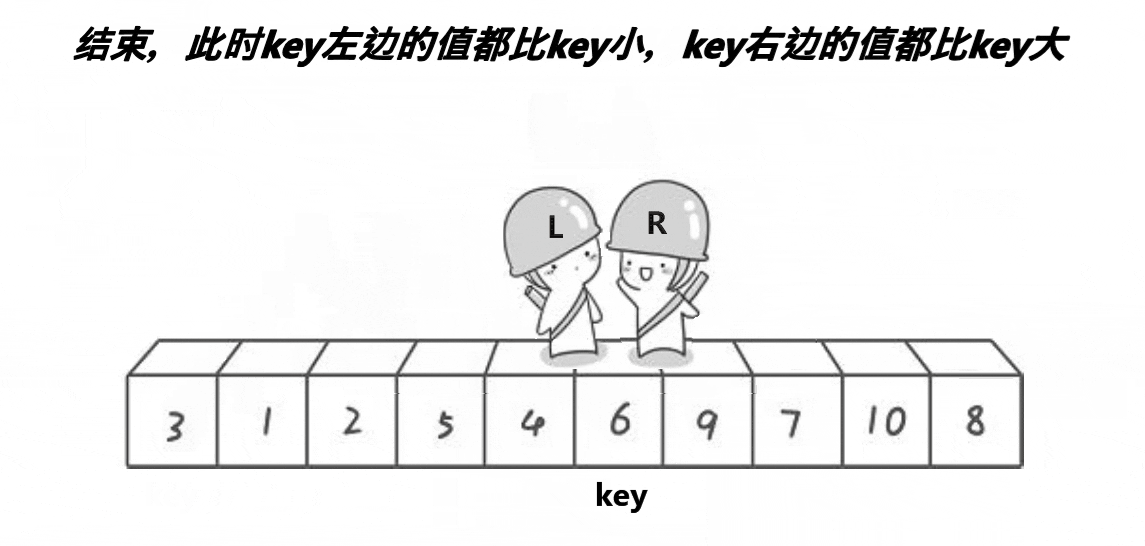
思考：为什么一定要让right比left先走呢❓❓❓

答：保证相遇位置比key小

right 未先遇到 left 的情况：right 从右向左遍历，会先找到一个比 key 小的元素并停下来，然后 left 从左向右遍历，找到比 key 大的元素后，两者交换位置。接着 right 继续向左走，left 继续向右走，重复上述过程。最终 left 向右靠近并与 right 相遇，由于 right 是停在比 key 小的值上，所以相遇位置是比 key 小的位置。
right 先遇到 left 的情况：left 先找到比 key 大的元素停下来，此时 right 与 left 进行交换，交换后 left 指向的值比 key 小。然后 right 继续向左走，可能会直接遇到 left，此时相遇位置同样比 key 小。

若选取数组右边的第一个数作为基准值 key，则通常让 left 指针先走，这样能保证相遇位置比 key 大。

代码实现

// 交换函数
void swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int PartSort1(int* arr, int begin, int end)
{int left = begin;int right = end;int keyi = begin;// 左指针小于右指针，循环继续while (left < right){while (left < right && arr[right] >= arr[keyi])//寻找比key小的值{right--;}while (left < right && arr[left] <= arr[keyi])//寻找比key大的值{left++;}swap(&arr[left], &arr[right]);}int mid = left;swap(&arr[keyi], &arr[mid]);return mid;
}void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}// 获取中间值int mid = PartSort1(arr, left, right);// 递归地对基准值左边的子数组进行快速排序  QuickSort(arr, left, mid - 1);// 递归地对基准值右边的子数组进行快速排序  QuickSort(arr, mid + 1, right);
}

(2)挖坑法

这种方法通过选择一个基准值（key），通常是数组的第一个元素，然后将数组分为两部分：一部分包含所有小于基准值的元素，另一部分包含所有大于基准值的元素。基准值最终位于这两部分的中间。

①设置 left 和 right 指针分别指向数组两端，选取数组首元素为基准值 key 并设起始位置为坑；
②right 从右往左找比 key 小的值放入坑位，形成新坑，left 从左往右找比 key 大的值放入坑位，更新坑位；
③left 与 right 相遇时，将 key 放入最后一个坑，记录位置为 mid；
④划分区间 [left，mid - 1] 与 [mid + 1,right] 重复上述步骤，直至不能划分。

下面我们来看个例子：

① 先定义变量key，存储数组第一个数作为key，此时left指向的位置就是坑。

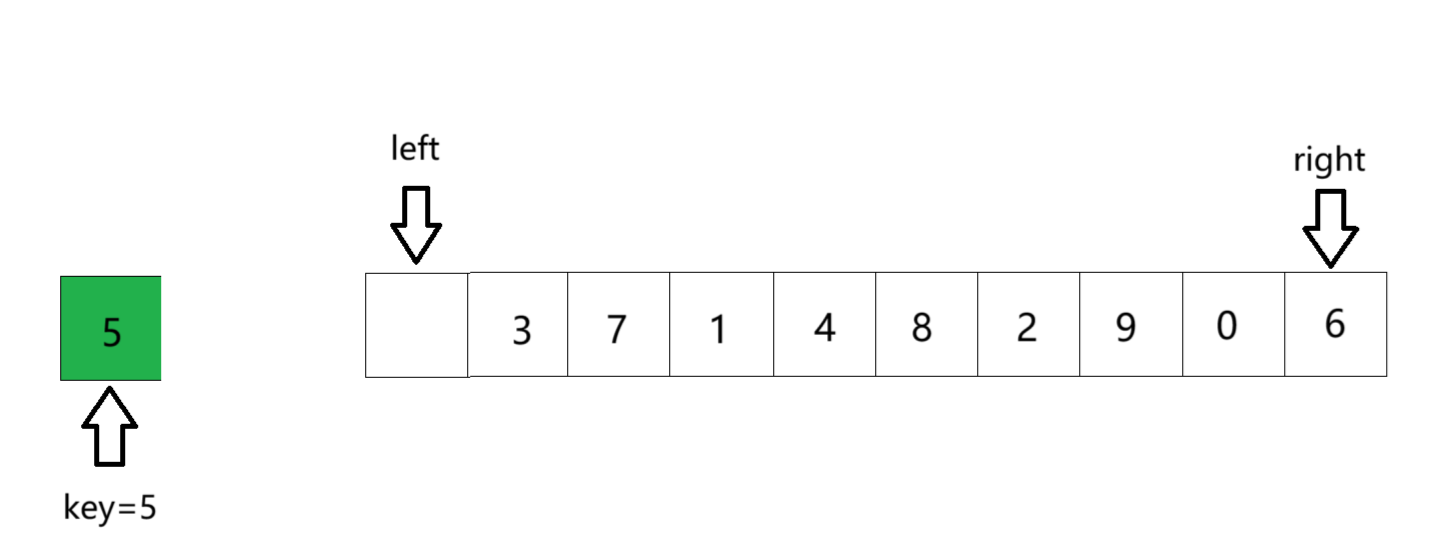
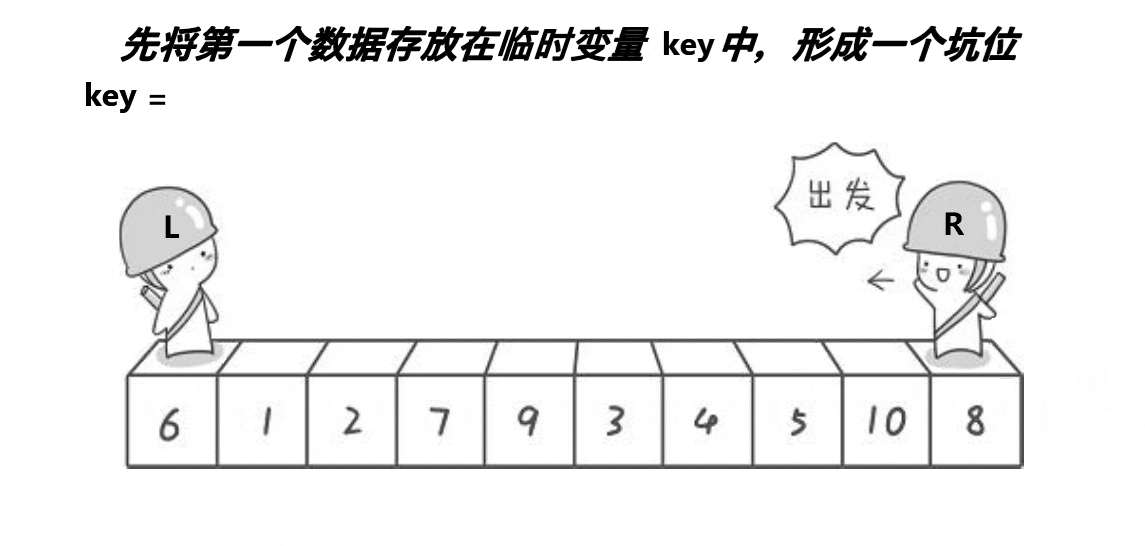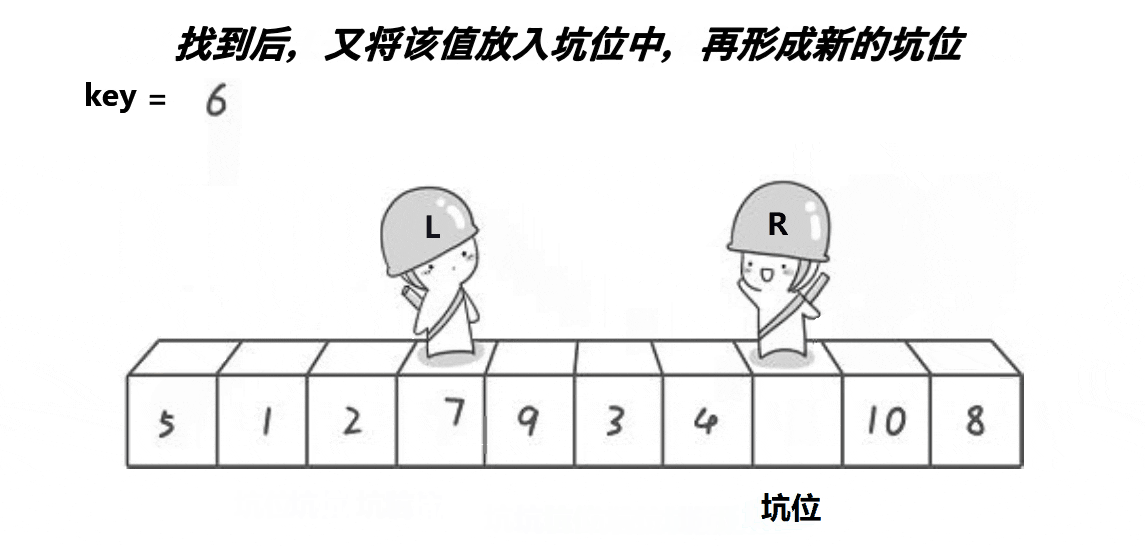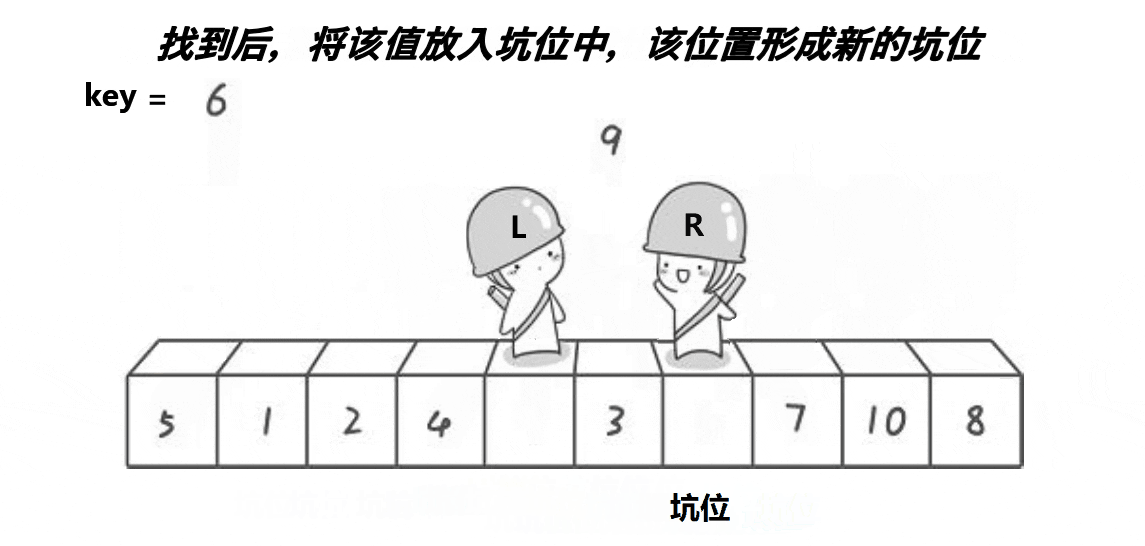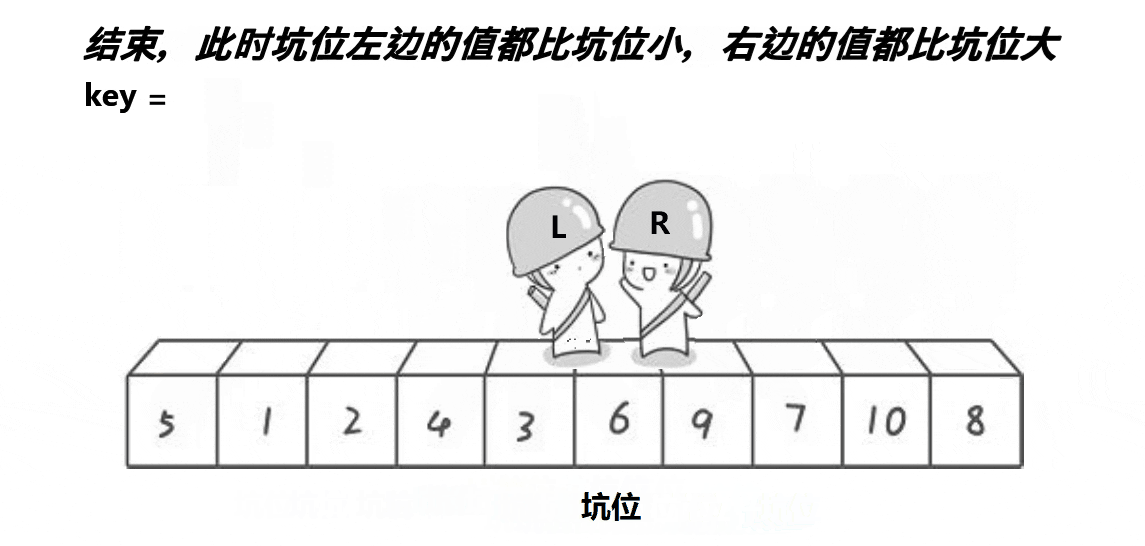
② right开始找小于key的数，找到后停止，将right位置的数放进坑里，此时right位置作为新的坑。

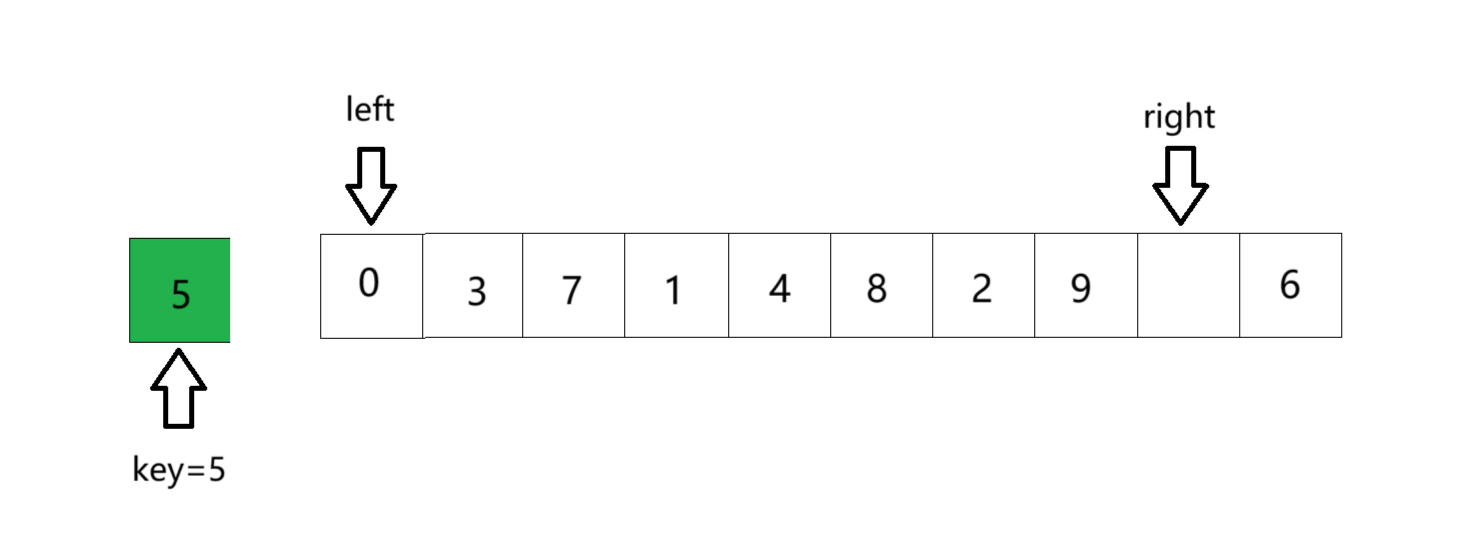
③ left行动寻找比key大的数，找到后停止，并将值放进坑里，此时left位置作为新坑。

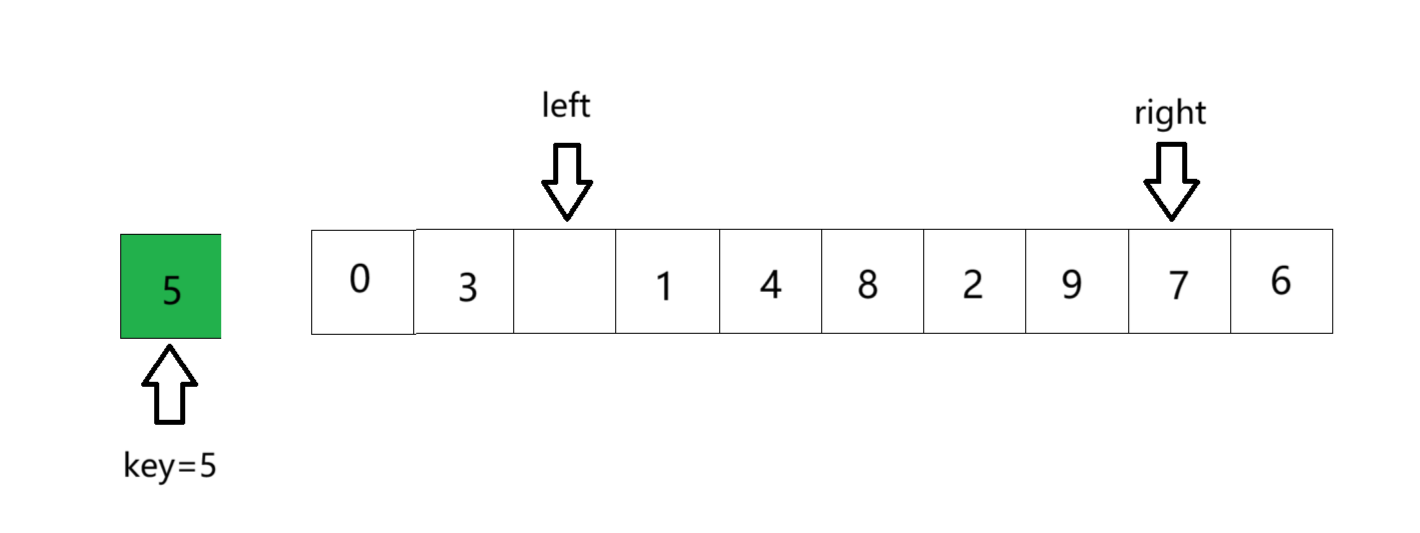
④ 以此循环，直到二者相遇。

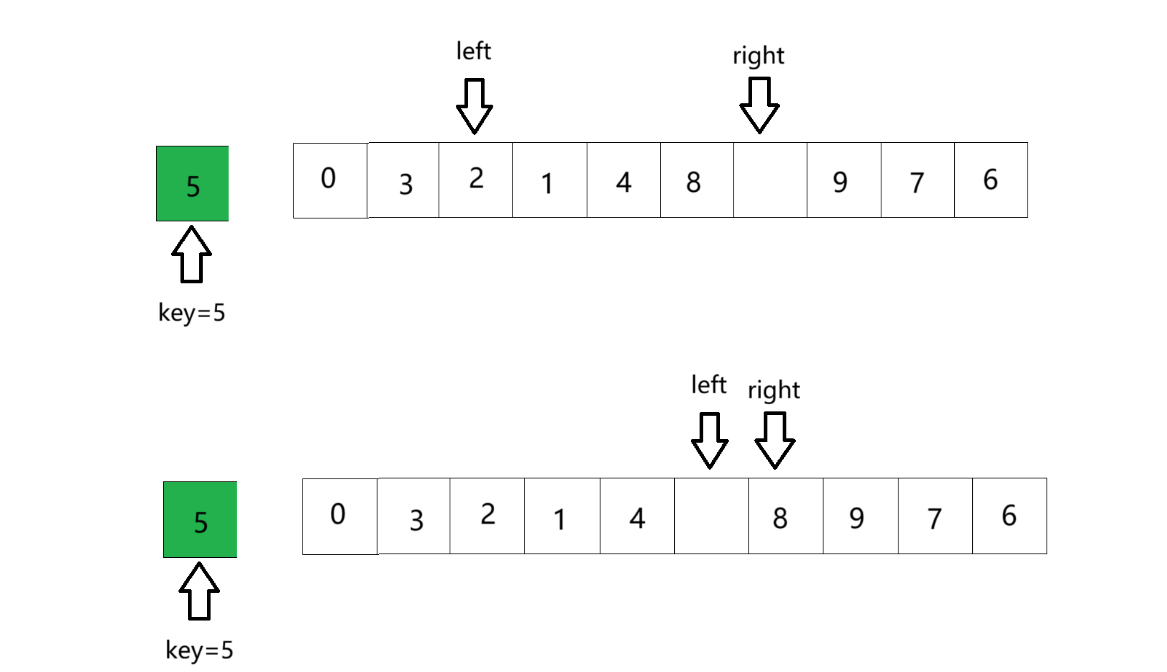
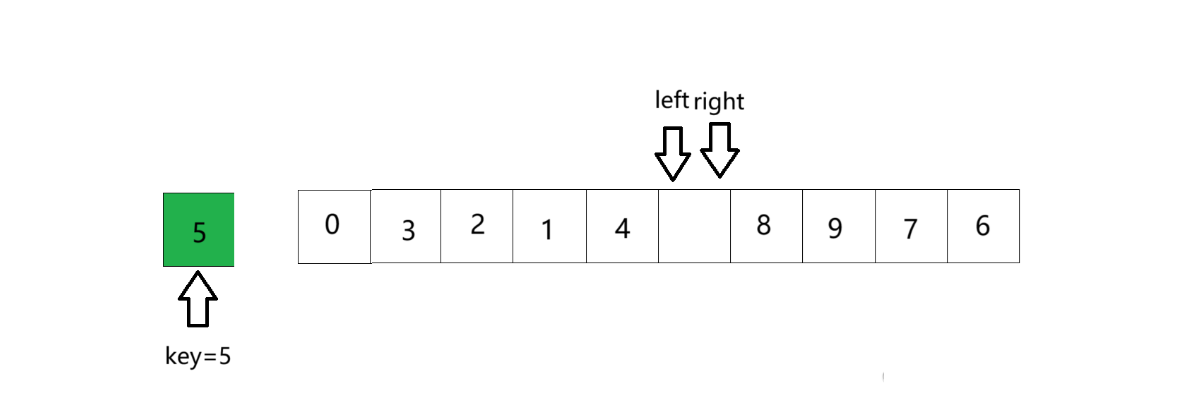
⑤ key值放到坑中，排序完毕，将key值下标返回。

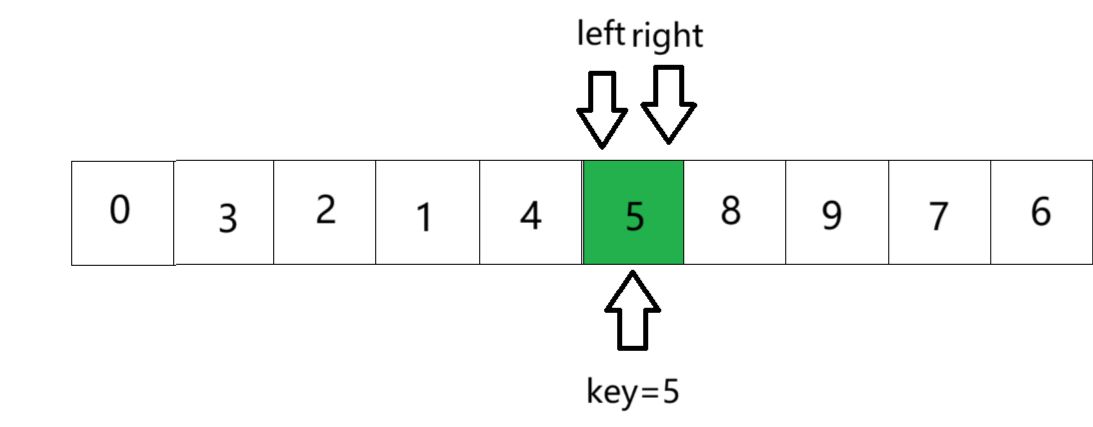
动图演示

代码实现

int PartSort2(int* arr, int begin, int end)
{int left = begin, right = end;int hole = begin;		// 记录当前需要填充的坑位（hole）int key = arr[left];	// 选取最左边的元素作为基准（key）while (left < right){// 从右向左扫描，找到第一个小于等于key的元素while (left < right && arr[right] >= key){right--;}// 将这个小于等于key的元素放到hole位置  arr[hole] = arr[right];hole = right; // 更新hole的位置// 从左向右扫描，找到第一个大于key的元素while (left < right && arr[left] <= key){left++;}// 将这个大于key的元素放到hole位置  arr[hole] = arr[left];hole = left; // 更新hole的位置  }// 循环结束时，left和right相遇，将基准元素放到正确的位置  arr[hole] = key;return hole; // 返回基准元素的位置
}
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}int mid = PartSort2(arr, left, right);//单趟排序// 递归地对基准元素左边的子数组进行快速排序  QuickSort(arr, left, mid - 1);// 递归地对基准元素右边的子数组进行快速排序  QuickSort(arr, mid + 1, right);
}

(3)前后指针法

①将数组第一个元素作为 key 基准值，定义前指针 prev 指向第一个数，后指针 cur 指向第二个数；
②cur 从左往右找比 key 小的值，找到后 ++prev，交换 prev 与 cur 指向的值，cur 继续遍历；
③cur 遍历完后，交换 prev 指向的值与 key，记录此时位置为 mid；
④划分区间 [left，mid - 1] 与 [mid + 1,right] 重复上述步骤，直至不能划分。

来看个例子：

①将数组第一个元素作为key基准值，定义前指针prev指向第一个数，后指针cur指向第二个数。cur从左往右依次遍历找key小的值。此时cur位置的数比key基准值小，所以prev加一后与cur位置的数交换，由于此时prev+1 == cur，所以交换后没有变化

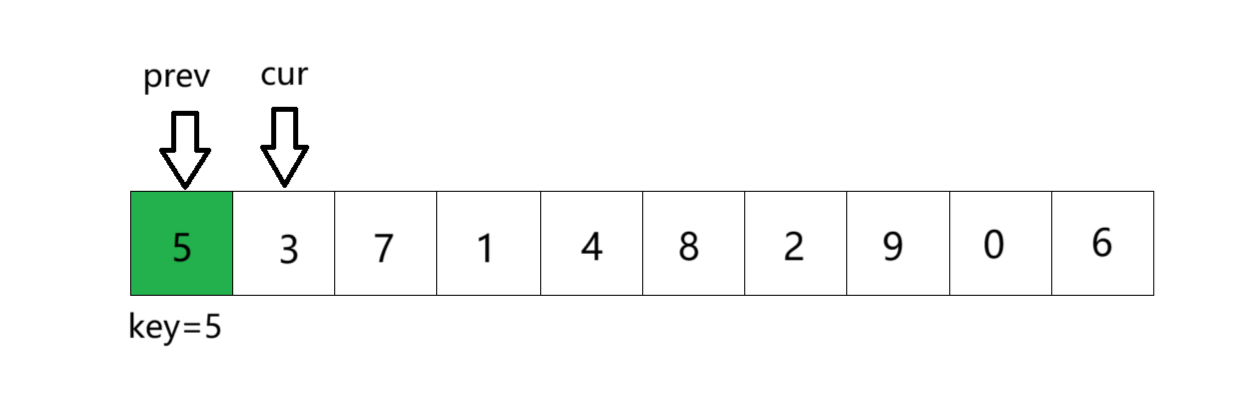
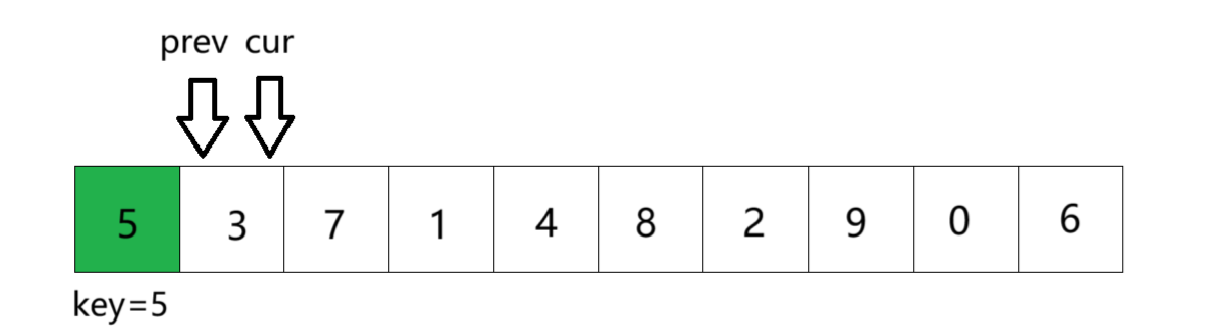
②cur继续走，找到比key小的数。找到后prev加一，交换二者的数。

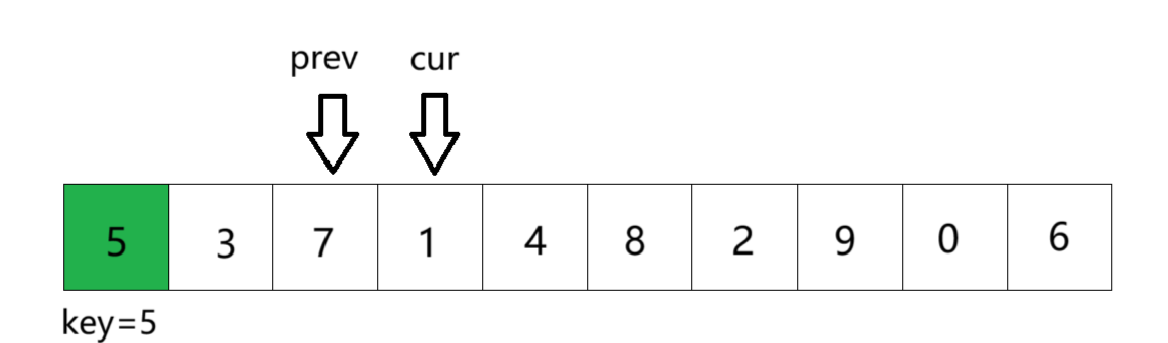
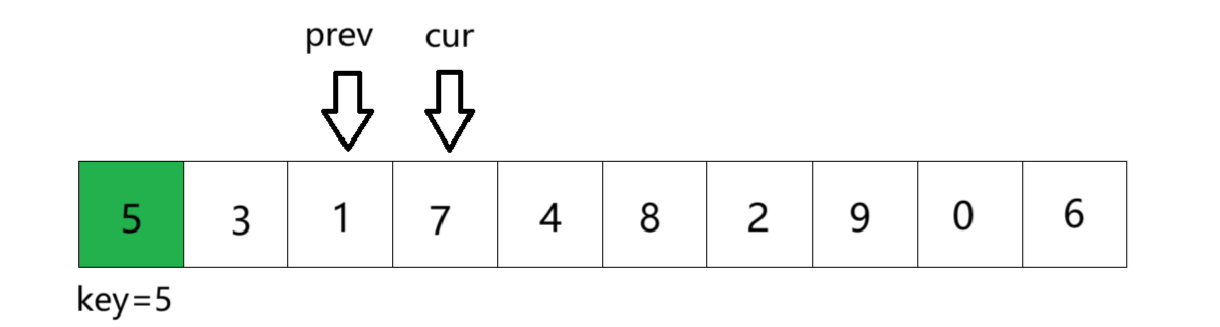
③重复以上步骤。

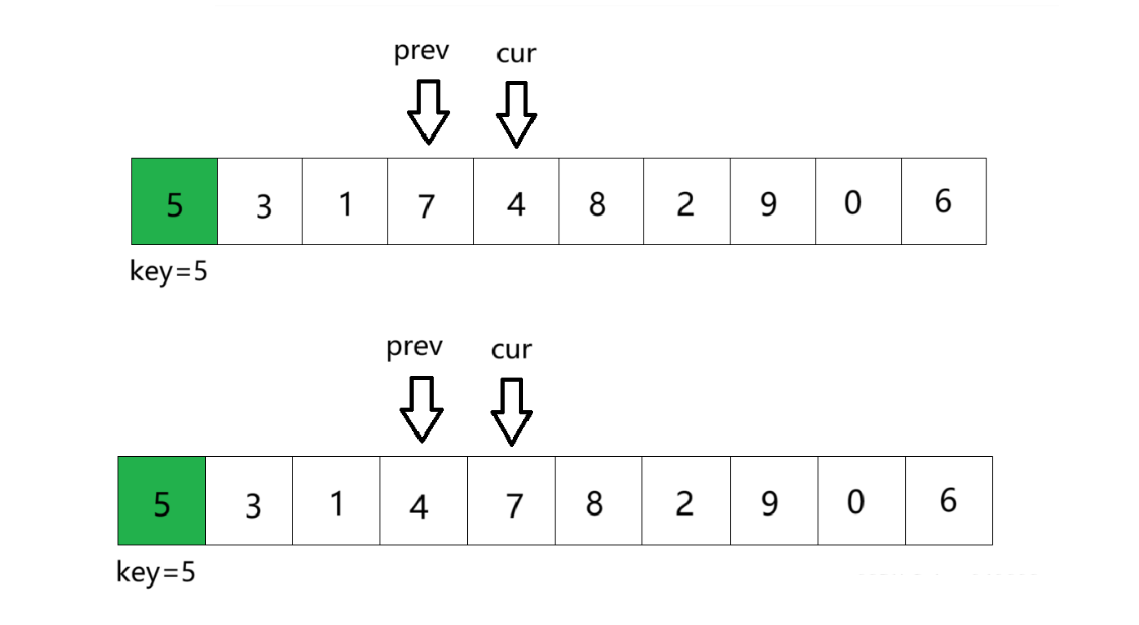
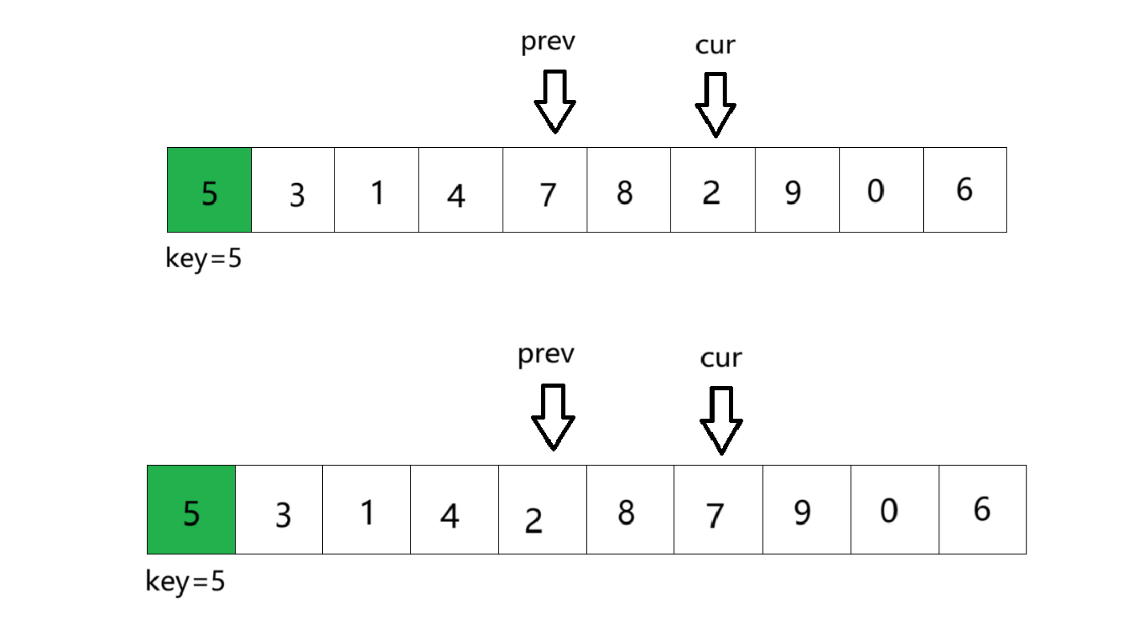
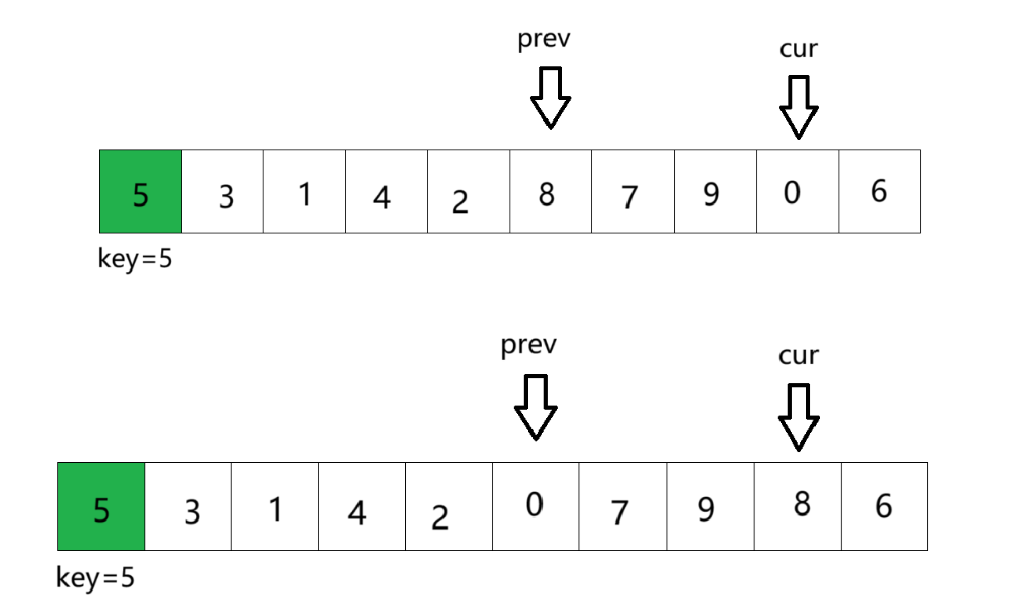
④cur遍历完数组，将prev与key交换数值，完成排序，并将key下标返回

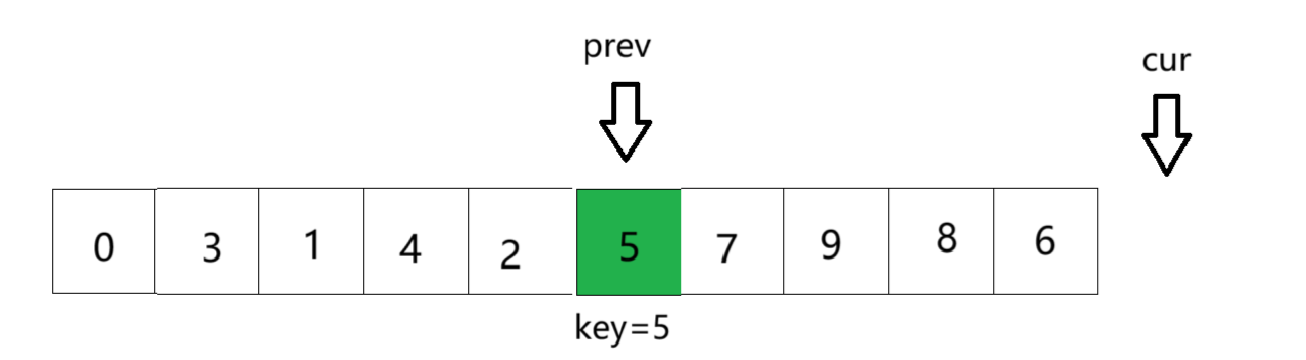
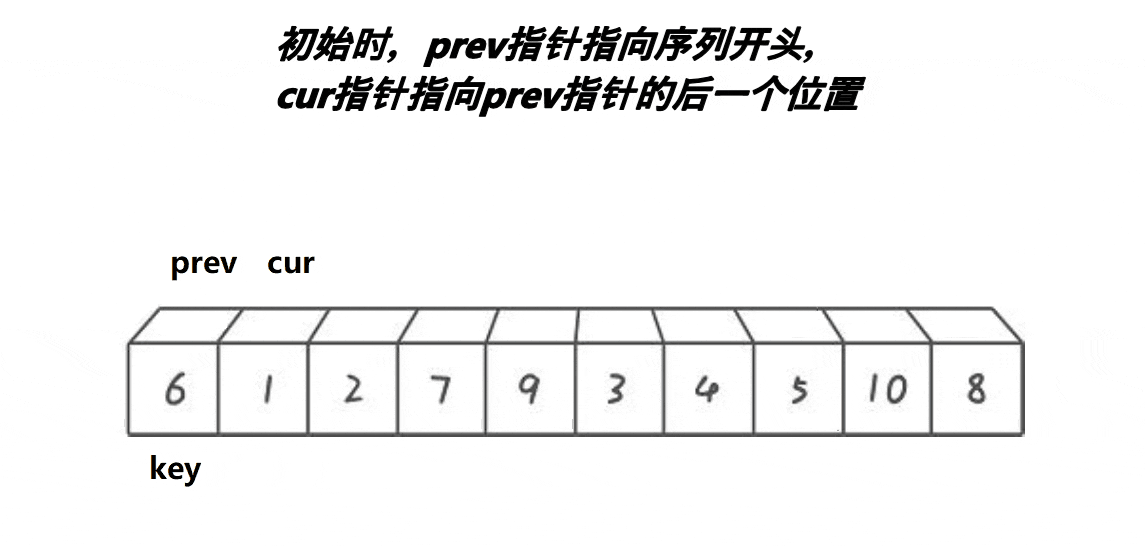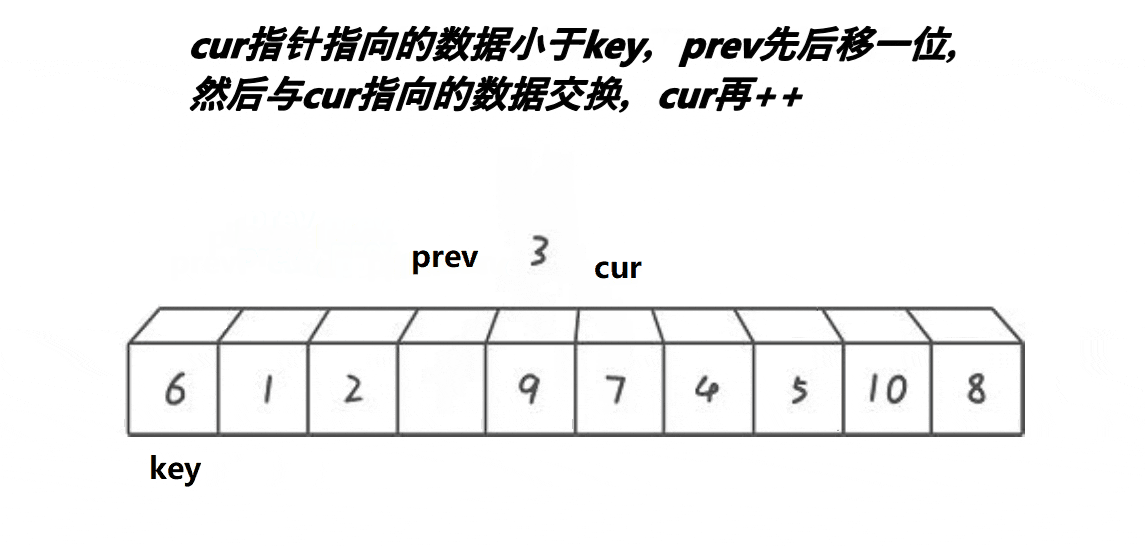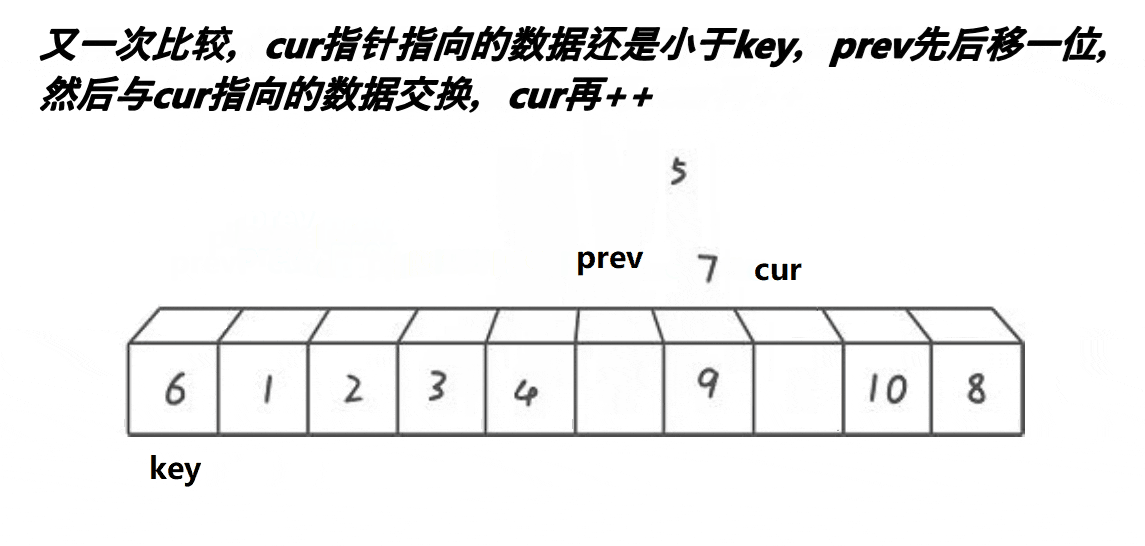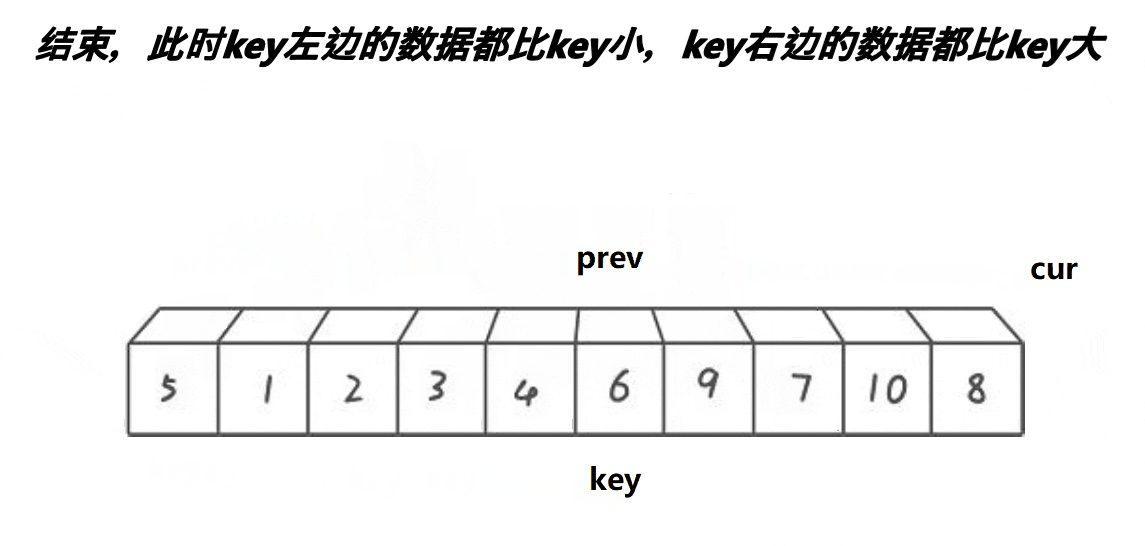
代码实现

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int PartSort3(int* arr, int begin, int end)
{int prev = begin;int cur = begin + 1;int keyi = begin;		// 基准元素的索引while (cur <= end)		// 遍历整个区间  {if (arr[cur] < arr[keyi])//小于则交换{// 将小于基准的元素与prev+1位置的元素交换，并递增prevSwap(&arr[++prev], &arr[cur]);}cur++;}Swap(&arr[prev], &arr[keyi]);// 返回基准元素的最终位置return prev;
}
void QuickSort(int* arr, int left, int right)
{if (left >= right)//不能划分{return;}int mid = PartSort3(arr, left, right);//单趟排序// 递归排序基准元素左边的子数组 QuickSort(arr, left, mid - 1);// 递归排序基准元素右边的子数组 QuickSort(arr, mid + 1, right);
}

3.复杂度分析

时间复杂度：通常情况下，快速排序需要递归 logN 层，每层都需遍历，时间复杂度为 O (NlogN)。但当基准值是数组中的最大或最小值（如有序数组排序且选首元素为基准）时，递归深度为 n，单趟排序也为 n，时间复杂度会变为 O (n²)。

空间复杂度：通常递归 logN 层，空间复杂度为 O (logN) 。若递归过深，如在最坏情况下，空间复杂度可能会接近 O (N)。

思考：由时间复杂度分析可知：当基准值是数组中的最大或最小值（如有序数组排序且选首元素为基准）时，递归深度为 n，单趟排序也为 n，时间复杂度会变为 O (n²)。这样子也会使得时间复杂度增大，使得排序效率极低，那么有没有办法改善呢❓

算法优化

改变基准值：若基准值为数组最值，会使递归深度加深、排序效率降低。可以采用随机数法，在数组中随机选择一个数作为基数，降低选到最大或最小值的概率；或者使用三数取中法，选取数组第一个、中间和最后一个元素中的中间值作为基准元素，减少最坏情况发生。
三指针分划区间：当数组重复元素较多时，普通快排效率降低。三指针分划区间定义 left、cur、right 三个指针，cur 遍历数组，根据 arr [cur] 与 key 的大小关系进行不同操作，最终将数组划分为小于 key、等于 key、大于 key 三个区间，提高排序效率。
区间优化：当递归到较深层级且子数组长度较短时，快速排序递归的函数调用和返回开销明显。可以设定数组长度下限阈值，当子数组长度小于阈值时，改用插入排序，提升效率。

逐一分析：

① 改变基准值

在我们选择基准值时，都是以数组中第一个数作为基准值进行排序，这样写的好处是非常方便且易懂，但是也有个大问题。
如果基准值是数组中的最大或最小值时，会导致快速排序的递归深度会非常深，排序效率会很低。
若是一个有序数组使用快速排序，则递归深度为n，单趟排序也为n，时间复杂度为O(n^2)。
为了防止出现这种情况，我们需要改变基准值：

1）随机数

在数组中随机选择一个数作为基数，每次都选到最大或最小的概率很小，但是有概率会选到最大或最小值。

#include <stdlib.h>
#include <time.h>
int GetRandIndex(int* arr, int left, int right)
{srand((size_t)time(NULL));	return rand() % (right-left+1) +left;
}

2）三数取中

int GetMid(int* arr, int left, int right)
{int mid = (left + right) / 2;if (arr[left] < arr[mid]){if (arr[mid] < arr[right]){return mid;}else if (arr[left] > arr[right]){return left;}else{return right;}}else   //arr[left] > arr[mid]{if (arr[mid] > arr[right]){return mid;}else if (arr[mid] > arr[left]){return left;}else{return right;}}
}

②三指针分划区间

除了数组有序的情况外，当数组的重复元素较多时，也会导致快排的效率降低。这时我们需要用上三指针分划区间。

三指针分划区间是快速排序算法中的一种分区策略，它主要用于处理包含多个相同基准值元素的数组。

1）步骤

一、核心定义：3 个指针的初始定位

算法通过 3 个指针划分数组，初始状态如下（假设数组下标从 0 开始）：

指针名称	初始指向位置	核心作用
left	数组首元素（下标 0）	标记 “小于 key 的区间” 的右边界（最终left左侧均为小于 key 的元素）
cur	数组第二个元素（下标 1）	遍历指针，负责逐个检查元素与 key 的大小关系
right	数组最后一个元素（下标len(arr)-1）	标记 “大于 key 的区间” 的左边界（最终`right`右侧均为大于 key 的元素）
key	划分基准值（需提前指定，如数组首元素、中间元素等）	作为划分标准，将数组分为 “小于、等于、大于” 三类元素

二、执行流程：cur 遍历与指针调整

cur从左向右遍历数组，根据arr[cur]与key的大小关系，执行 3 种操作，直至cur > right（遍历终止条件）：

当arr[cur] < key：
交换arr[cur]与arr[left]（将 “小于 key 的元素” 归入left左侧的区间）；
同时cur++（继续遍历下一个元素）、left++（“小于 key 的区间” 右边界右移）。

当arr[cur] > key：
交换arr[cur]与arr[right]（将 “大于 key 的元素” 归入right右侧的区间）；
仅right--（“大于 key 的区间” 左边界左移），不移动 cur（因为交换后cur指向的新元素未检查过）。

当arr[cur] == key：
无需交换，直接cur++（“等于 key 的元素” 自然落在中间区间，继续遍历下一个元素）。

三、最终结果：3 个区间的明确划分

遍历终止（cur > right）后，数组被精准划分为 3 个不重叠的连续区间，区间范围固定：

区间类型	区间范围（下标）	区间内元素特点
小于 key	`[begin, left-1]`（`begin`为数组起始下标，通常是 0）	所有元素严格小于`key`
等于 key	[left, right]	所有元素等于`key`
大于 key	`[right+1, end]`（`end`为数组结束下标，通常是`len(arr)-1`）	所有元素严格大于`key`

2）代码实现

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int GetMid(int* arr, int left, int right)
{int mid = (left + right) / 2;if (arr[left] < arr[mid]){if (arr[mid] < arr[right]){return mid;}else if (arr[left] > arr[right]){return left;}else{return right;}}else   //arr[left] > arr[mid]{if (arr[mid] > arr[right]){return mid;}else if (arr[mid] > arr[left]){return left;}else{return right;}}
}void ThreeDivision(int* arr, int* left, int* right)
{int key = arr[*left];		// 以数组的第一个元素作为基准值int cur = *left + 1;		// 从数组的第二个元素开始遍历while (cur <= *right){if (arr[cur] < key)		// 如果当前元素小于基准值{// 与left指向的元素交换，并移动left和curSwap(&arr[(*left)++], &arr[cur++]);}else if (arr[cur] > key){// 与right指向的元素交换，并移动right  // 注意：这里不移动cur// 因为新交换到cur位置的值可能需要再次比较Swap(&arr[cur], &arr[(*right)--]);}else{cur++;}}
}
void QuickSort(int* arr, int begin, int end)
{if (begin >= end){return;}	int mid = GetMid(arr, begin, end);Swap(&arr[begin], &arr[mid]);int left = begin;int right = end;ThreeDivision(arr, &left, &right);//三指针划分区间//[begin, left - 1][left, right][right + 1, end]// 递归排序基准元素左边的子数组 QuickSort(arr, left, mid - 1);// 递归排序基准元素右边的子数组 QuickSort(arr, mid + 1, right);
}

③区间优化

在快速排序算法中，当递归到较深层级且处理的子数组长度较短时，继续使用递归快速排序可能会导致效率降低。

为什么效率会降低❓：

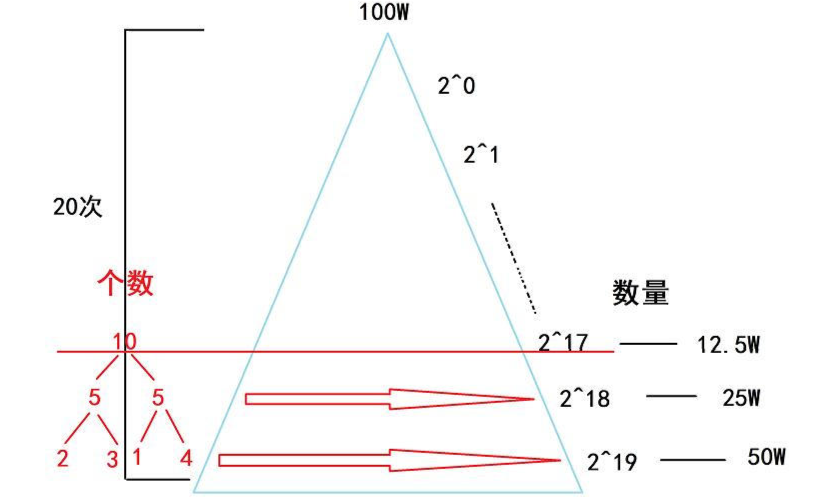
快速排序的递归类似于二叉树的形式，每次递归调用都会涉及函数调用和返回的开销，包括保存和恢复调用栈的上下文。当递归层级很深且处理的子问题规模很小时，这些开销会变得更加明显：

递归调用开销占比升高：短子数组排序本身计算量小，而每次递归的函数上下文保存等开销占比大幅增加，拖慢整体效率；
栈空间占用与溢出风险：递归层级深，栈空间消耗多，可能引发溢出，即使未溢出也影响系统性能；
缓存利用率低：短子数组数据难有效利用缓存，数据访问开销增大；
难借局部有序性：深层子数组常具局部有序性，快排无法利用，而适合的算法（如插入排序）未被启用，效率相对偏低。

为了优化这种情况，可以设定一个数组长度的下限阈值。当子数组长度小于这个阈值时，不再采用递归快速排序，而是改用效率更高的插入排序算法。

void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//数组长度小于10时，调用插入排序if (right - left + 1 < 10){InsertSort(arr + left, right - left + 1);return;}int mid = PartSort3(arr, left, right);//单趟排序// 递归排序基准元素左边的子数组 QuickSort(arr, left, mid - 1);// 递归排序基准元素右边的子数组 QuickSort(arr, mid + 1, right);
}

非递归实现

当递归太深时会存在栈溢出的风险，因此，为了避免这种风险我们除了采用尾递归优化空间外，我们还可以采用非递归的形式实现快速排序。

非递归实现的方法需要使用数据结构——栈，利用其后进先出的形式模拟实现递归。

如果不太清楚的可以看看这篇文章[数据结构——lesson6.栈]

实现步骤

初始化：检查传入的数组区间是否有效，若begin >= end，则无需排序，直接返回。创建一个栈用于存储子区间的起始和结束下标，并将待排序数组的初始区间(begin, end)的起始和结束下标压入栈中。
循环处理：当栈不为空时，进入循环。从栈中弹出当前区间的结束下标end和起始下标begin。
单趟排序：对当前区间(begin, end)进行单趟排序，找到基准值key的正确位置keyi。
确定并压入子区间：根据基准值的位置keyi，将当前区间划分为左右两个子区间(begin1, end1)和(begin2, end2)。若右子区间(begin2, end2)包含多于一个元素，则将其起始和结束下标压入栈中；同理，若左子区间(begin1, end1)包含多于一个元素，也将其起始和结束下标压入栈中。通常先压入右子区间再压入左子区间，以符合递归快速排序的前序遍历顺序。
重复处理：回到步骤 2，继续处理栈中的下一个区间，直到栈为空。此时，所有子区间都已排序完毕，非递归快速排序结束。
销毁栈：最后，销毁栈，释放其占用的内存资源。

void QuickSortNonR(int* arr, int left, int right)
{ST st;STInit(&st);// 将初始的排序范围（整个数组）的左右边界压入栈中STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){// 先从栈中弹出的为左边界int begin = STTop(&st);STPop(&st);// 后从栈中弹出的为右边界int end = STTop(&st);STPop(&st);// 对当前子数组进行分区，并返回基准值的最终位置int keyi = PartSort(arr, begin, end);// 区间划分为[begin, keyi-1] keyi [keyi+1, end]// 如果基准值右侧还有元素需要排序// 则将右边界和基准值右侧第一个元素的索引压入栈if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}// 如果基准值右侧还有元素需要排序// 则将右边界和基准值右侧第一个元素的索引压入栈if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);
}

结束语

本节说到了快排有三种递归的方法，分别是挖坑法、左右指针法以及前后指针法，而且还有非递归的写法，为的就是防止递归太深导致的栈溢出问题

下文我们将介绍两种外部排序算法——归并排序与计数排序

感谢你的三连支持！！！