C++基础(13)——list类的模拟实现
目录
一、接口函数和类总览
二、节点结构体的实现
构造函数
三、迭代器结构体的实现
迭代器模版参数
构造函数
重载++运算符
重载--运算符
重载==运算符
重载*运算符
重载->运算符
四、list的模拟实现
默认成员函数
构造函数
拷贝构造函数
赋值运算符重载函数
析构函数
迭代器相关函数
访问容器的相关函数
插入和删除函数
insert
erase
push_back和pop_back
push_front和pop_front
其他函数
size
clear
empty
swap
一、接口函数和类总览
我们想要实现list类,需要一个节点的结构体,一个迭代器结构体,还要有一个list类。
总览:
#include <cstddef>
#include <initializer_list>
#include <iostream>
#include <assert.h>namespace xywl {// 首先,我们需要一个节点类,带模版参数的template<class T>struct list_node {T _data;list_node<T>* _next;list_node<T>* _prev;list_node(const T& data = T()) : _data(data), _next(nullptr), _prev(nullptr) {}};// list的迭代器template<class T, class Ref, class Ptr>struct list_iterator {typedef list_node<T> Node;typedef list_iterator<T, Ref, Ptr> Self;Node* _node;list_iterator(Node* node):_node(node){}Ref operator*();Ptr operator->();Self& operator++();Self& operator--();Self& operator++(int);Self& operator--(int);bool operator!=(const Self& s) const;bool operator==(const Self& s) const;};// list类的实现template<class T>class list {typedef list_node<T> Node;public:typedef list_iterator<T, T&, T*> iterator;typedef list_iterator<T, const T&, const T*> const_iterator;iterator begin();iterator end();const_iterator begin() const;const_iterator end() const;void empty_init();list();list(std::initializer_list<T> in);list(const list<T>& t);list<T>& operator=(list<T> t);~list();void clear();void swap(list<T>& t);void push_back(const T& x);void push_front(const T& x);iterator insert(iterator pos, const T& x);void pop_back();void pop_front();iterator erase(iterator pos);size_t size() const;bool empty() const;Node* _head;size_t _size;};
}二、节点结构体的实现
我们首先要明确一点,就是我们实现的list类在底层是一个带头节点的双向循环链表。所以我们实现节点的时候要有前驱和后继指针。如图:

所以我们在实现节点类的时候,就需要存储如下几个信息:数据,前驱节点的地址和后继节点的地址。
所以说我们这个结构体只需要实现一个构造函数即可:
构造函数
这里我们默认给两个指针传入空指针,数据默认是指定类型的默认构造函数传入的值:
template<class T>
struct list_node
{T _data;list_node<T>* _next;list_node<T>* _prev;list_node(const T& data = T()) : _data(data), _next(nullptr), _prev(nullptr) {}
};三、迭代器结构体的实现
我们这里就会十分好奇,之前我们也没有单独实现一个迭代器结构体,为什么这里要实现呢?
这是因为之前我们实现的string类和vector类都是在一个连续的空间里面的,我们可以通过原生的指针实现自增、自减和解引用的操作。但是我们实现list是链表,链表的节点在内存中的位置可是随机的,我们不可能通过使用节点指针的自增和自减操作来实现对节点的数据进行操作的。所以我们这里需要实现迭代器结构体。
所以我们这里需要对于节点指针进行封装,对于节点操作的各个运算符进行合理地重载。
迭代器模版参数
我们这里可以看到我们在实现迭代器结构体的模板参数列表中传入了三个模板参数:
template<class T, class Ref, class Ptr>我们这里T就是我们数据类型,Ref(reference)是引用类型,Ptr(pointer)是指针类型。
同时我们的list类的模拟实现里面,有两种迭代器类型:
typedef list_iterator<T, T&, T*> iterator;
typedef list_iterator<T, const T&, const T*> const_iterator;我们这里之所以要实现两种,是因为我们要满足不同的使用需求。
我们还需要说明一下,我们在实现迭代器对象的时候也将参数模版重定义了:
typedef list_iterator<T, Ref, Ptr> Self;构造函数
我们这里实现的迭代器结构体实际上就是分装了一个节点的指针,归根到底还是对指针的操作。所以我们这里的构造函数的实现就是对于指针的赋值了:
list_iterator(Node* node):_node(node) {}重载++运算符
我们这里需要实现两种++操作,分别是前置++和后置++:
前置++:
我们实现前置++就是返回自增后的数据,实现起来也非常简单:
Self& operator++() {_node = _node->_next;return *this;
}后置++:
和前置++不同,我们需要返回++之前的值,所以我们需要用临时变量先存储一下我们的当前的对象的成员,然后再自增,最后返回那个临时变量:
Self& operator++(int) {Self temp(*this);_node = _node->_next;return temp;
}重载--运算符
这里的逻辑和++雷同,也是实现两个:
前置--:
Self& operator--() {_node = _node->_prev;return *this;
}后置--:
Self& operator--(int) {Self temp(*this);_node = _node->_prev;return temp;
}重载==运算符
我们使用等于的运算符的时候,只需要判断这两个迭代器是不是同一个位置的迭代器即可,也就是判断迭代器中的指针的指向是不是相同的:
bool operator==(const Self& s) const {return _node == s._node;
}重载*运算符
我们使用借用的时候就是要获取到这个位置的数据内容即可,也就是返回当前接待的指针所指向的数据即可:
Ref operator*() {return _node->_data;
}重载->运算符
我们在使用迭代器的时候有可能会使用到->运算符,比如我们的list容器存储的类型不是内置类型而是自定义类型,我们在拿到了一个位置的迭代器的时候,就需要使用->来访问成员:
Ptr operator->() {return &_node->_data;
}这里我们有可能会有一个疑问,就是我们重载了->符号,但是我们只是获得了对应数据的地址,也就是说我们还要调用一次->符号才能获取到正真的数据(第一个箭头是调用了重载函数返回指针,第二个箭头才是指针取访问对象中的成员),但是事实上我们只需要使用一个箭头,这是因为我们的编译器做了识别处理,为了增加可读性省略了一个箭头,但是我们还是要明白这里的过程。
四、list的模拟实现
默认成员函数
构造函数
这里就是我们之前学习到的只是了,我们在创建一个双向循环的链表的时候,初始化的状态是申请了一个头节点,然后让这个节点的前驱指针和后继指针都是指向自己的,如图:
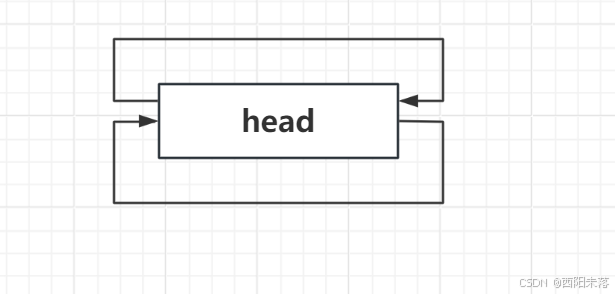
void empty_init() {_head = new Node;_head->_next = _head;_head->_prev = _head;_size = 0;
}
list() {empty_init();
}注意:我们这里为了让代码更加美观,就把初始化动作单独封装成了一个函数。
拷贝构造函数
这里的实现逻辑比较简单,就是先初始化出来一个节点,然后我们遍历传进来的list的每一个节点,然后将这每一个节点都尾插到开始创建的对象里面:
list(std::initializer_list<T> in) {empty_init();for(auto& s : in) {push_back(s);}
}赋值运算符重载函数
我们的赋值运算符重载函数有两种常见的写法,这里和我们之前的string类的模拟实现可以说是一模一样了:
写法一:传统写法
这里的实现逻辑比较容易理解,就是先将原来的对象清空,然后将传入的对象里面的数据一个一个的尾插到我们清空的对象里面:
lsit<T>& operator=(const list<T>& in) {if(this != &in) {clear();for(auto& s : in) {push_back(s);}}return *this;
}写法二:现代写法
这里也是用到了swap函数来进行操作,这种写法的原理和之前是想string的原理如出一辙就不多说了。
list<T>& operator=(list<T> t) {swap(t);return *this;
}析构函数
析构函数就是将对象中的每一个节点都释放,然后将头节点置空即可:
~list() {clear();delete _head;_head = nullptr;
}迭代器相关函数
我们首先需要实现的就是获取begin和end这两个迭代器,我们根据带头双向循环链表的基本定义,我们就可以知道begin就是头节点的下一个节点,而我们的end就是最后一个有效数据的下一个节点也就是头节点了。
iterator begin() {return _head->_next;
}
iterator end() {return _head;
}我们这里还需要实现一个const对象的相关函数:
const_iterator begin() const
{return _head->_next;
}
const_iterator end() const
{return _head;
}访问容器的相关函数
我们这里主要是实现back和front这两个函数,一个返回第一个有效数据,一个返回最后一个有效数据即可:
T& front() {return *begin();
}T& back() {return *(--end());
}插入和删除函数
insert
这里的实现逻辑需要一些之前学习链表的知识了,为了简化操作,我们可以保存住当前位置的指针和前驱指针,当然了如果你不嫌麻烦也可以不保存直接实现对应的逻辑,最后要返回新的节点的迭代器,我们可以根据下面的图来尝试:
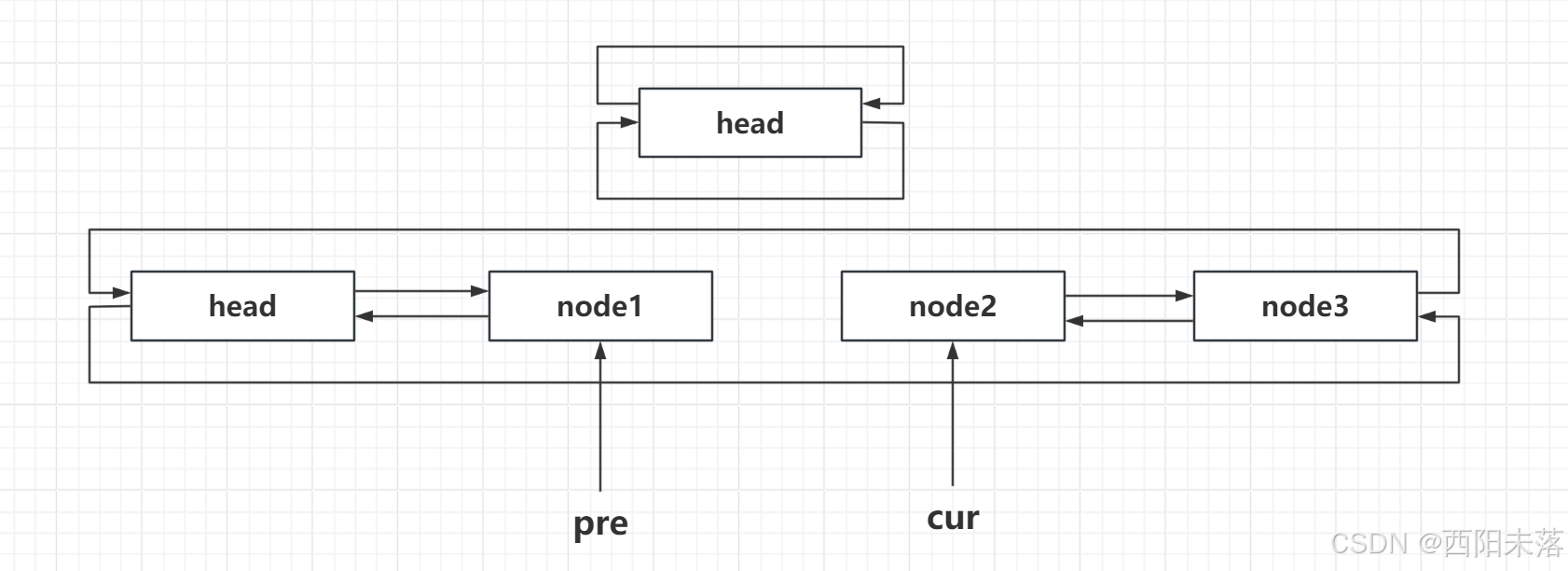
iterator insert(iterator pos, const T& x) {Node* cur = pos._node;Node* prev = cur->_prev;Node* newnode = new Node(x);newnode->_next = cur;cur->_prev = newnode;prev->_next = newnode;newnode->_prev = prev;++_size;return newnode;
}erase
我们首先要建立没有该位置节点的连接关系,然后删除该节点,最后返回下一个位置的迭代器:
iterator erase(iterator pos) {assert(pos != end());Node* prev = pos._node->_prev;Node* next = pos._node->_next;next->_prev = prev;prev->_next = next;delete pos._node;_size--;return next;
}push_back和pop_back
其实这里的两个操作完全可以复用我们实现的insert函数和erase函数,也就是下面的代码:
void push_back(const T& x) {insert(end(), x);
}
void pop_back() {erase(--end());
}push_front和pop_front
这里的实现也是可以完全的复用之前的insert和erase函数:
void push_front(const T& x) {insert(begin(), x);
}
void pop_front() {erase(begin());
}其他函数
size
我们这里就是要返回有效的数据个数,而我们在定义成员的就考虑到了这个情况,所以我们只需要返回_size:
size_t size() const {return _size;
}clear
这个函数就是清空对象中的节点的函数,我们只需要遍历一遍,然后删除每一个节点就行了:
void clear() {auto it = begin();while(it != end()) {it = erase(it);}
}empty
这个函数就是判断是不是空,我们这里因为提前定义了_size,所以只需要判断_size是不是空的:
bool empty() const {return _size == 0;
}swap
这个函数就是用来交换我们的头节点指针和我们的有效数据个数的,我们这里需要在前面加上std::的作用域限定符,告诉编译器我们是用的库函数提供的swap而不是自己实现的:
void swap(list<T>& t) {std::swap(_head, t._head);std::swap(_size, t._size);
}五、总的实现代码
#include <cstddef>
#include <initializer_list>
#include <iostream>
#include <assert.h>namespace xywl {// 首先,我们需要一个节点类,带模版的template<class T>struct list_node {T _data;list_node<T>* _next;list_node<T>* _prev;list_node(const T& data = T()) : _data(data), _next(nullptr), _prev(nullptr) {}};// list的迭代器template<class T, class Ref, class Ptr>struct list_iterator {typedef list_node<T> Node;typedef list_iterator<T, Ref, Ptr> Self;Node* _node;list_iterator(Node* node):_node(node){}Ref operator*() {return _node->_data;}Ptr operator->() {return &_node->_data;}Self& operator++() {_node = _node->_next;return *this;}Self& operator--() {_node = _node->_prev;return *this;}Self& operator++(int) {Self temp(*this);_node = _node->_next;return temp;}Self& operator--(int) {Self temp(*this);_node = _node->_prev;return temp;}bool operator!=(const Self& s) const {return _node != s._node;}bool operator==(const Self& s) const {return _node == s._node;}};template<class T>class list {typedef list_node<T> Node;public:typedef list_iterator<T, T&, T*> iterator;typedef list_iterator<T, const T&, const T*> const_iterator;iterator begin() {return _head->_next;}iterator end() {return _head;}const_iterator begin() const{return _head->_next;}const_iterator end() const {return _head;}void empty_init() {_head = new Node;_head->_next = _head;_head->_prev = _head;_size = 0;}list() {empty_init();}list(std::initializer_list<T> in) {empty_init();for(auto& s : in) {push_back(s);}}list(const list<T>& t) {empty_init();for(auto& s : t) {push_back(s);}}list<T>& operator=(list<T> t) {swap(t);return *this;}~list() {clear();delete _head;_head = nullptr;}void clear() {auto it = begin();while(it != end()) {it = erase(it);}}void swap(list<T>& t) {std::swap(_head, t._head);std::swap(_size, t._size);}void push_back(const T& x) {insert(end(), x);}void push_front(const T& x) {insert(begin(), x);}iterator insert(iterator pos, const T& x) {Node* cur = pos._node;Node* prev = cur->_prev;Node* newnode = new Node(x);newnode->_next = cur;cur->_prev = newnode;prev->_next = newnode;newnode->_prev = prev;++_size;return newnode;}void pop_back() {erase(--end());}void pop_front() {erase(begin());}iterator erase(iterator pos) {assert(pos != end());Node* prev = pos._node->_prev;Node* next = pos._node->_next;next->_prev = prev;prev->_next = next;delete pos._node;_size--;return next;}size_t size() const {return _size;}bool empty() const {return _size == 0;}private:Node* _head;size_t _size;};
}
