[温习C/C++]0x06 坐标系中矩形重叠类问题分析
系列文章目录
[温习C/C++]0x00-STL标准模板库概述
[温习C/C++]0x01-STL泛型算法-持续更新长文版
[温习C/C++]0x03-sort排序
[温习C/C++]0x04 C++刷题基础编码技巧
[温习C/C++]0x05 C++刷题技巧—set自定义排序及查找
C++刷题技巧—坐标系中矩形重叠类问题分析
- 系列文章目录
- 更新日志
- 问题描述
- 正向判断重叠
- 分析思路
- 反向判断重叠
- 分析思路
更新日志
| 日期 | 变更内容 |
|---|---|
| 2025-09-14 | 完成初稿 |
问题描述
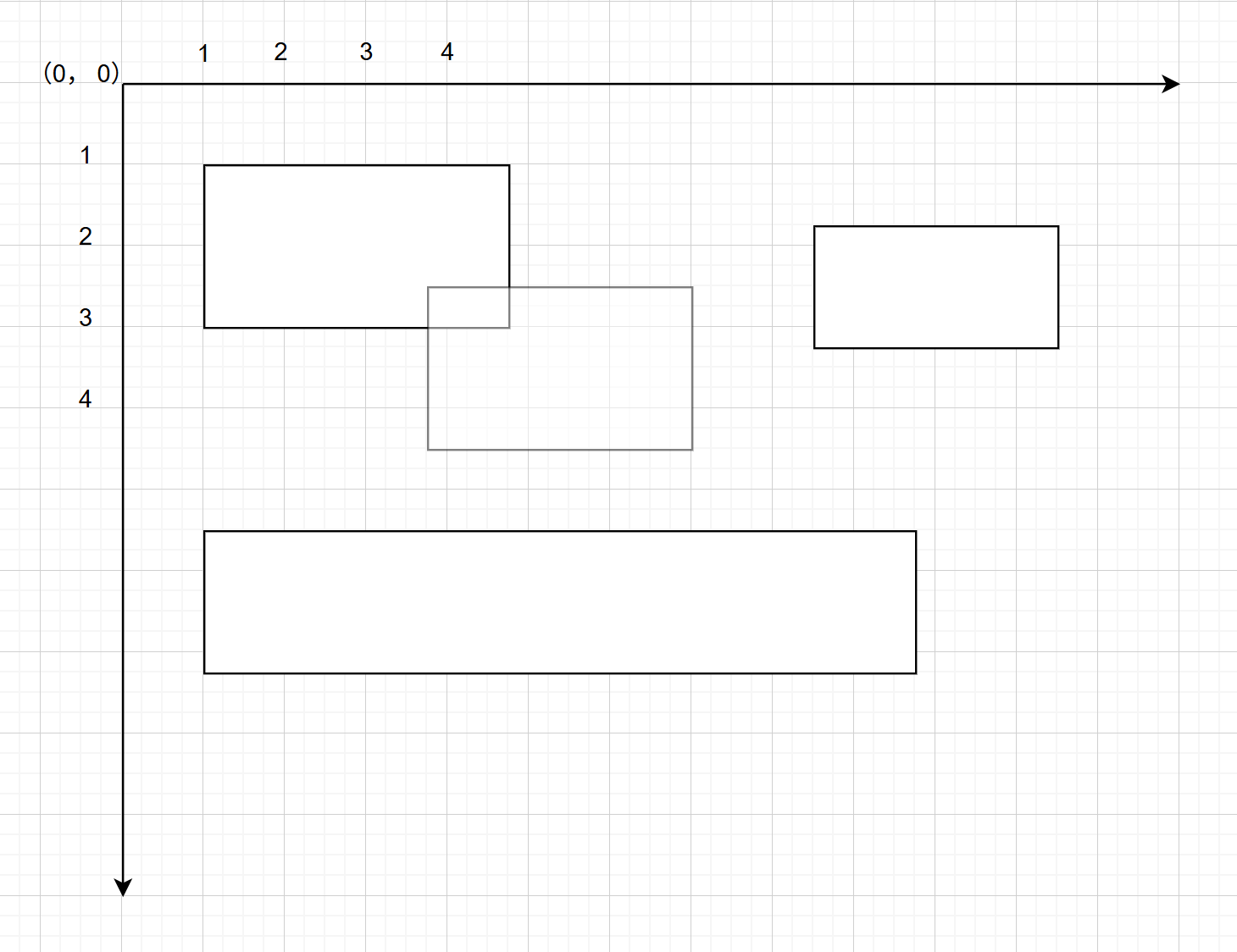
如图所示,当前需要在坐标系内绘制矩形,那如何判断新绘制的矩形与已有的矩形是重合的? 如果重合则不可以绘制;同时,可以要求消除重叠的所有矩形。
正向判断重叠
判断哪些情况下两个矩形会重叠。
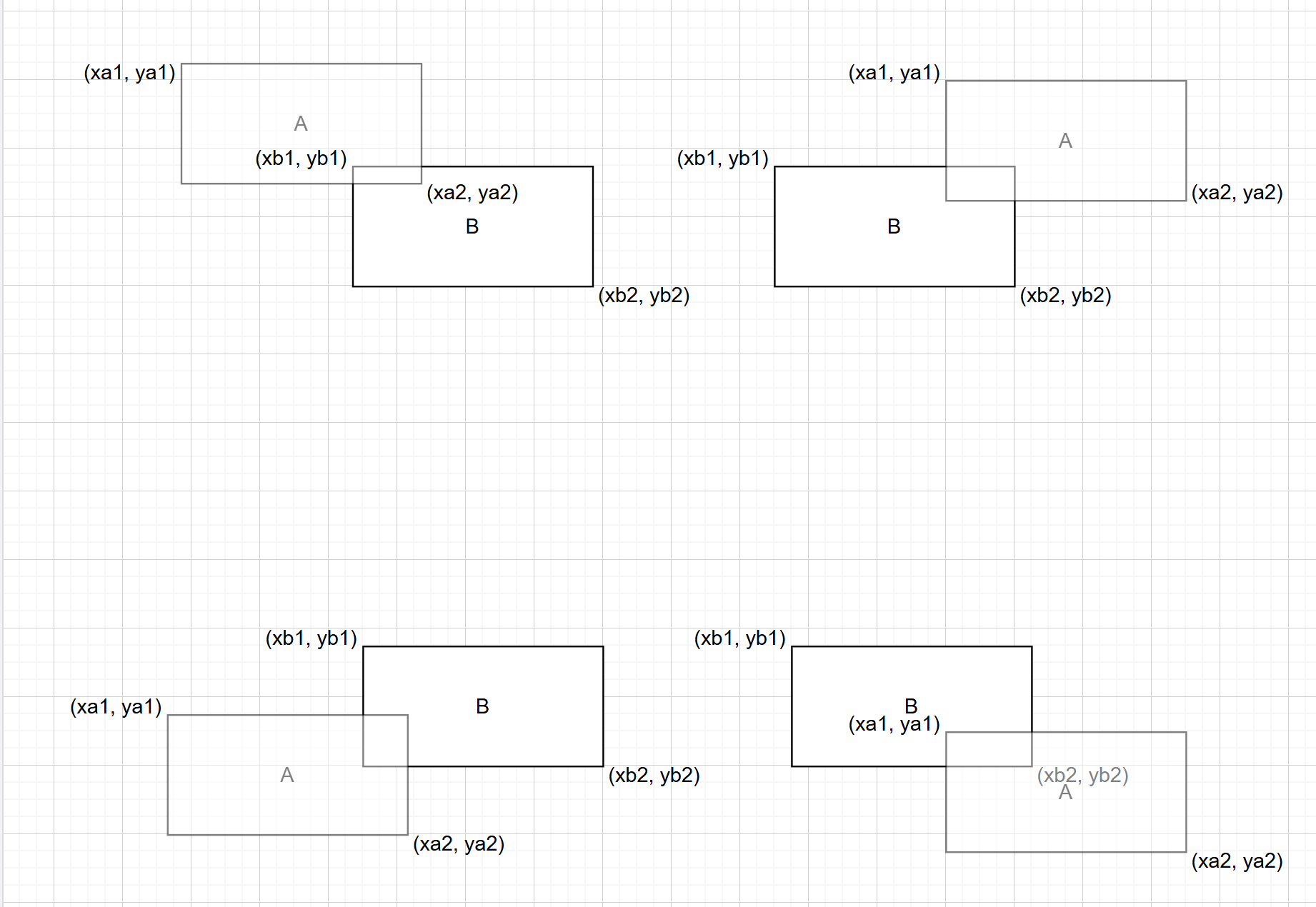
可判断矩形A的四个角是否在矩形B内,只要任意一个角位于矩形B内,则两个矩形是重叠的。
如果矩形A完全在矩形B内,则A的四个角都在矩形B内。
分析思路
分别将矩形A的左上角开始坐标(xa1, ya1) 和 B的右下结束角坐标(xb2, yb2)比较;A右下角结束坐标(xa2, ya2)和 B左上角开始坐标(xb1, yb1)做比较。
观察以上图形,可以得到以下结论:
- A矩形开始行 xa1 <= B矩形结束行 xb2
- A矩形开始列 ya1 <= B矩形结束列 yb2
- A矩形结束行 xa2 <= B矩形开始行 xb1
- A矩形结束列 ya2 <= B矩形开始列 yb1
即同时满足以上四个条件则,矩形重合。
反向判断重叠
哪些场景是不重合的?
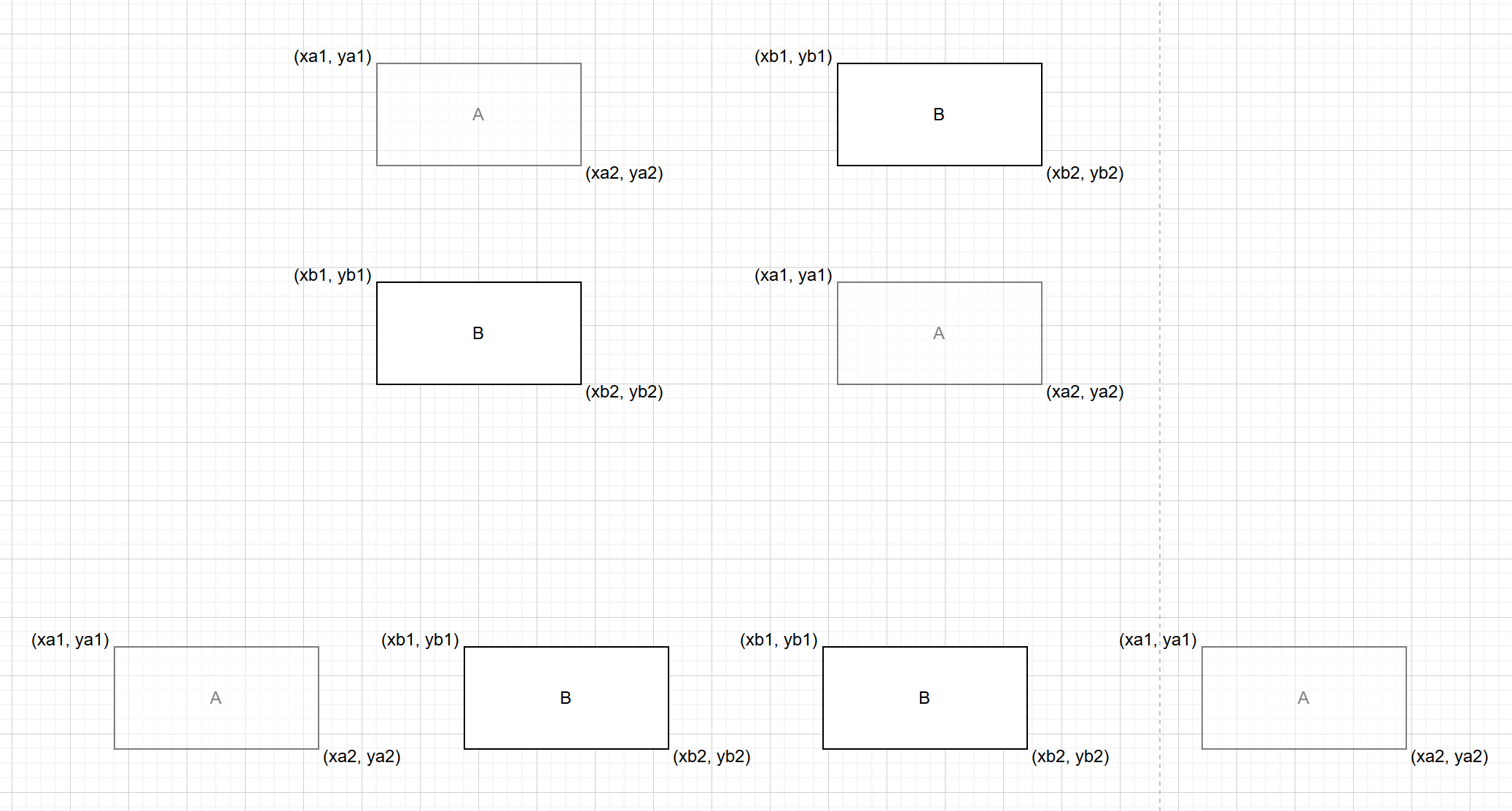
分析思路
A在B上方,A在B下方,A在B左侧,A在B右侧。
- A在B上方: xa2 > xb1
- A在B下方: xa1 < xb2
- A在B左侧: ya2 < yb1
- A在B右侧: ya1 > yb2
以上四个条件只要满足其中一个就能说明这两个矩形不重合。
