枚举：扫雷

题目：P2327 [SCOI2005] 扫雷 - 洛谷

题目概述：给你雷的信息位置，最多有几种雷旳摆放方案？

思路：雷的位置不同的方案其实就两个。

• 第一个位置没有雷
• 第一个位置有雷

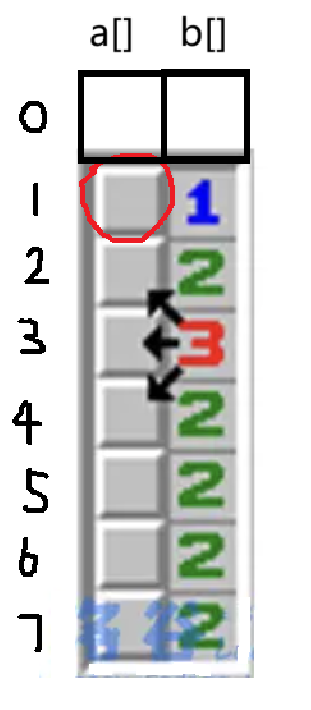
我们可以根据第一个位置，推算出接下来的位置有几个雷。

雷的数量 = 雷的个数 - 雷周边一圈的雷。

1. 假设第一个位置没有雷 （a[1] = 0）

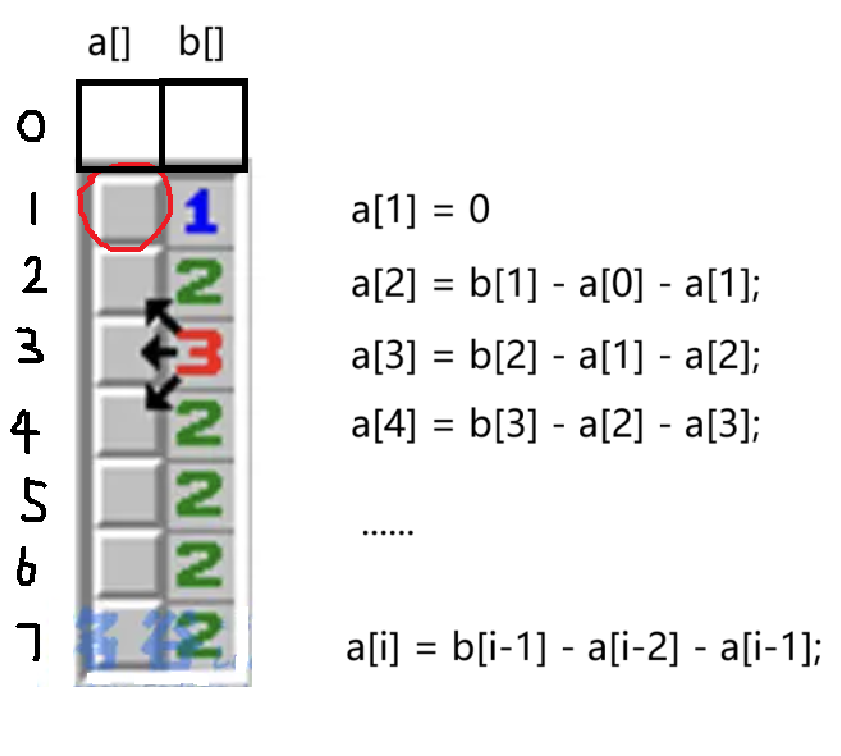
2. 假设第一个位置有雷  （a[1] = 1）

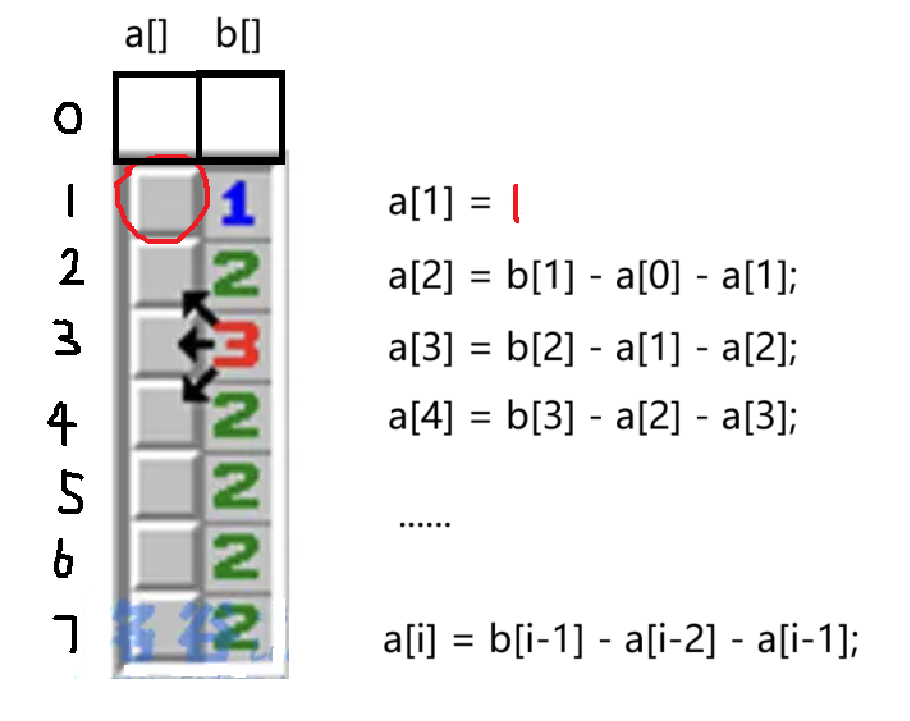
无论哪种方案，我们最后都可以 得出公式：a[i] = b[i-1] - a[i-2] - a[i-1];

一个位置，只有两个可能，要么有雷，有么没有雷。

如果a[i]这个位置雷的数量 < 0 或者 > 1，说明这个雷的摆放方案不存在！所以每次计算完a[i]，都要判断a[i]是否符合范围。

另外注意，a[n+1]位置的雷的数量必须等于0。这个比较容易忽略。（否则说明摆放方案不存在）

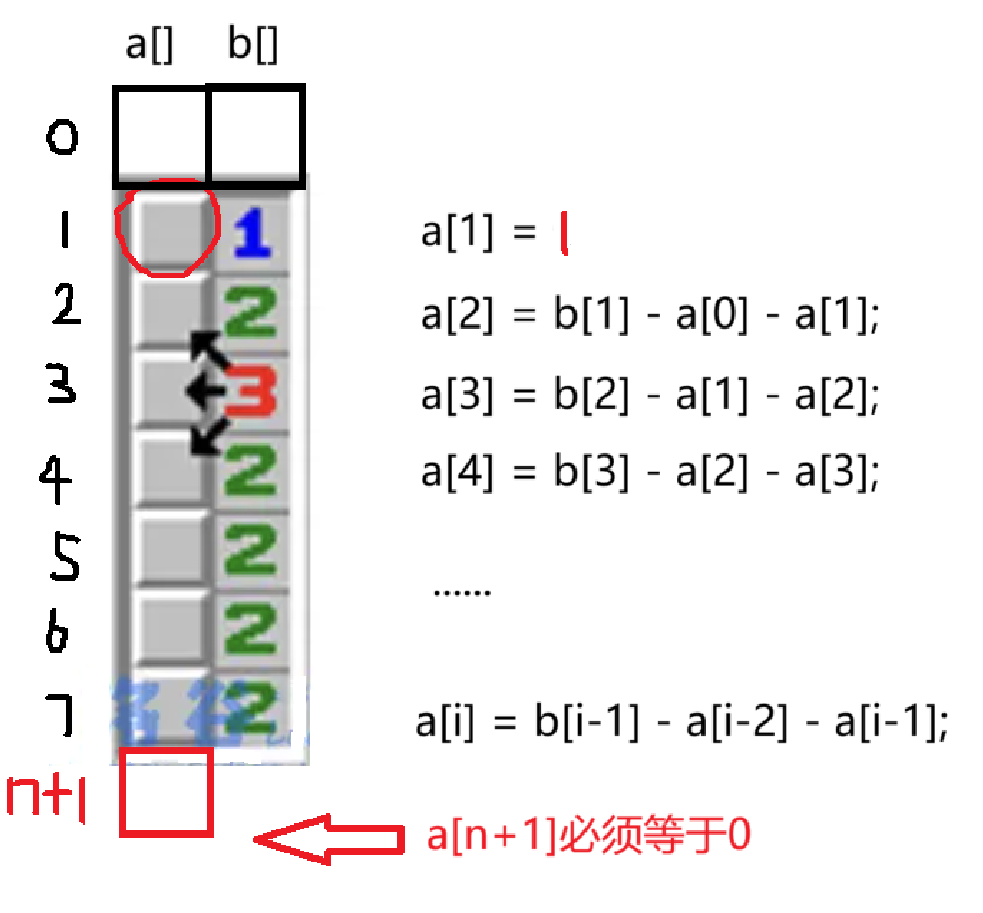
总结：假设第一个位置有雷和没有雷。计算a[i]雷的个数，雷的个数要符合基本条件，a[i]位置的雷必须是0或者1，a[n+1]位置的雷必须是0。

#include <iostream>using namespace std;
const int N = 1e4 + 10;int a[N], b[N];
int n;//可以设置两个函数，一个有雷，一个没有雷
int check1()
{a[1] = 1;   for (int i = 2; i <= n; i++)  //注意i的循环从2开始{a[i] = b[i-1] - a[i-2] - a[i-1];if (a[i] < 0 || a[i] > 1) return 0;}a[n+1] =  b[n] - a[n-1] - a[n];if (a[n+1] != 0) return 0;return 1;
}int check2()
{a[1] = 0;for (int i = 2; i <= n; i++){a[i] = b[i-1] - a[i-2] - a[i-1];if (a[i] < 0 || a[i] > 1) return 0;}a[n+1] =  b[n] - a[n-1] - a[n];if (a[n+1] != 0) return 0;return 1;
}int main()
{cin >> n;for (int i = 1; i <= n; i++) cin >> b[i];cout << check1() + check2() << endl; return 0;
}

该代码的时间复杂度为 ​​O(n)​​。

• 主函数中的循环用于读取输入数组 b，执行次数为 n，因此时间复杂度为 O(n)。

• 函数 check1和 check2各自包含一个从 2 到 n 的循环，因此每个函数的时间复杂度为 O(n)。

总时间复杂度为 O(n) + O(n) = O(n)。