当前位置：首页 > news >正文

机器学习（三）：决策树

news 2025/9/15 10:10:29

决策树

$\hspace{1.68em}$ 在之前的线性回归和逻辑回归的章节中，我们已经知道机器学习可以按照提出的数据模型进行拟合或者分类，那么是否有可能通过一种结构实现这两种功能？可以使用决策树这种模型

分类任务

$\hspace{1.6em}$ 我们总想通过尽可能少的时间判断出一个有 n 个特征的对象属于哪一类别，有时采集的样本中不需要确定所有特征的取值，就已经能够判断有这部分的特征的对象所属类别，那么这样的背景就让树这种结构可以发挥加速判别的作用，为了应对各种可能的对象特征，怎么采用一个固定的结构去判别不确定的对象？
$\hspace{1.6em}$ 此时怎么设计树的节点关系，即判别的顺序非常重要，可以通过以下几种指标：

熵
信息论中将量化揭开不确定面纱的程度的指标称为熵，熵越大，说明依照当前的判别结构，能够得到的信息越少。其数学表达为： $-\sum_{i=1}^{n} p_i \log_2 p_i$ ，
GINI 系数
GINI 系数是一种衡量数据不纯度（或不确定性）的指标，用于反映数据分布的集中程度。其取值范围在 0 到 1 之间
对于有 K 个类别的数据集，假设某节点中第 i 类样本的比例为 $p_i$ ，则该节点的 GINI 系数定义为： $Gini=1−∑i=1Kpi2\text{Gini} = 1 - \sum_{i=1}^K p_i^2$

两种判别指标的差异

计算复杂度：GINI 系数无需计算对数，计算效率更高，尤其适合大规模数据。
平滑性：GINI 系数是二阶导数连续的函数，而熵函数（涉及对数）在极值点附近变化更敏感。
实际应用：CART 算法默认使用 GINI 系数，ID3/C4.5 算法使用熵和信息增益。

有了判别指标怎么去构造决策树？

构建决策树

下面用一个例子来进行分类，通过四个特征判断当前对象对应的label应该是yes，还是no

F1-AGE	F2-WORK	F3-HOME	F4-LOAN	label
0	0	0	0	no
0	0	0	1	no
0	1	0	1	yes
0	1	1	0	yes
0	0	0	0	no
1	0	0	0	no
1	0	0	1	no
1	1	1	1	yes
1	0	1	2	yes
1	0	1	2	yes
2	0	1	2	yes
2	0	1	1	yes
2	1	0	1	yes
2	1	0	2	yes
2	0	0	0	no

构建决策树的递归算法框架

根据上面提到的指标确定当前特征中最能降低不确定性的那个特征
从未分类的分类特征集中去掉上一步确定的特征，再把该特征添加到已经分类好的特征集中
按照该特征的不同取值，将数据集进行切分，不同的切分情况对应不同的子树，也就是说，一个子树应该通过特征 + 特征取值两者同时确定

每次函数调用都确定出当前层应该选择的最优分类特征，其函数头为

createTree(dataset,labels,featLabels)

表示的是按照当前的数据集 dataset，基于已经分类好的特征集 featLabels 中，从当前的未分类的特征集 labels 中选出当前的最优分类特征，并构造一颗子树连接到当前的位置中

直到出现以下两种情况后停止构造子树：
case1: 当前数据集中的所有标签均取同样的值
case2: 当前数据集中的特征只剩一个
对于 case2, 可能存在虽然特征1个，但是对应的标签类别数量却大于等于2，此时应该通过多数选择法，将数据集中出现的标签数量最多的作为当前子树的节点值返回

$\hspace{1.68em}$ 通过判别指标能够确定决策树中节点的父子关系，但是决定最后训练效果的还是在测试集上的正确率，所以模型训练完毕之后必须考虑其过拟合问题，与之前的线性回归和逻辑回归模型中引入超参数的正则化方法不同，决策树模型更多考虑的是数的形状作为正则化的手段

决策树针对过拟合问题中的正则化方法

对于决策树来说，对树的形状进行限制往往能抑制过拟合问题，这种限制可以通过算法进行实现，主要可以从两种角度进行限制

对迭代终止条件的设定，这种设定又分为三类

控制数的叶子节点的数量：min_samples_split（节点在分割之前必须具有的最小样本数），min_samples_leaf（叶子节点必须具有的最小样本数），max_leaf_nodes（叶子节点的最大数量），
控制每个节点的分支数量：max_features（在每个节点处评估用于拆分的最大特征数）
控制决策树的最大深度：max_depth(树最大的深度)

在选择特征作为决策节点的时候就进行预处理

引入 C4.5 算法作为选择特征的判断方法，C4.5 算法用 $Gain(A)IV(A)\text{Gain Ratio}(A) = \frac{\text{Information Gain}(A)}{\text{IV}(A)}$ 其中 $IV(A)\text{IV}(A)$ 是节点的自身熵，计算方法是 $∑i=1m∣Di∣∣D∣log⁡2(∣Di∣∣D∣)\sum_{i=1}^{m} \frac{|D_i|}{|D|} \log_2 \left( \frac{|D_i|}{|D|} \right)$ ，这个算法能够有效抑制某个节点的分支过多的情况
C4.5的改进CART树，每一个分类节点只用考虑属于某一特征或者不属于某一特征，那么最终构建的决策树就会是一颗二叉树

其他问题

$\hspace{1.68em}$ 对于分类场景，需要明确的是有可能存在以下问题：

即使是在训练集上，也可能存在当输入各个特征的取值之后，决策树能够得到的只是具有最大可能性的类别，
决策树（如 DecisionTreeClassifier）默认通过轴平行的超平面划分特征空间，这导致了决策树对数据方向非常敏感，比如对于下面的分类问题：

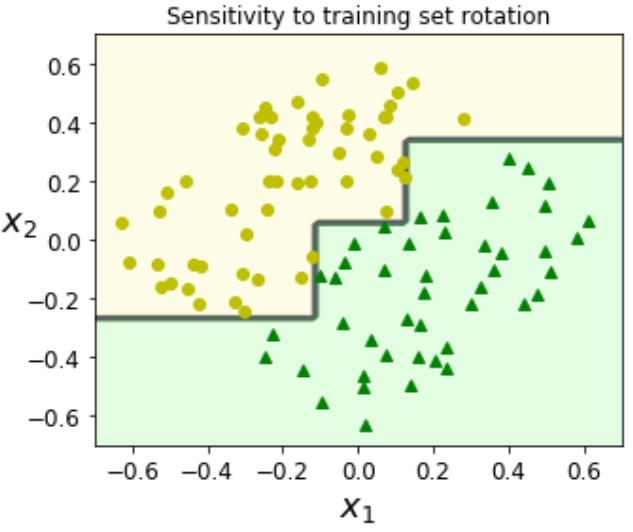
$\hspace{1.68em}$ 这里的边界变多，模型复杂度增加：树的深度和节点数增多，这个特点就需要我们使用各种方法对数据的特征进行正则化，注意这里不是模型训练本身需要正则化，而是数据的特征选取并不是最优。这种现象也可称为 特征间的共线性特征。
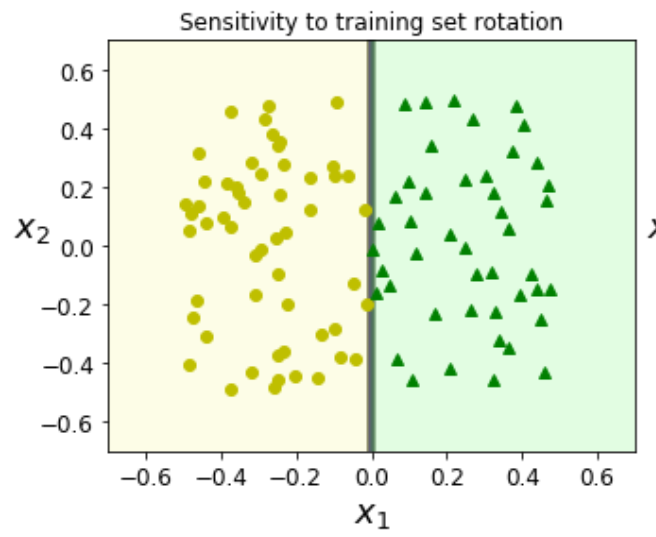
$\hspace{1.68em}$ 解决的方案，PCA：主成分分析法，本质上就是对现有特征进行线性变换，让两个特征正交，对[x1, x2]进行线性变换之后变成下图所示的样子：
在这里插入图片描述