当前位置：首页 > news >正文

LSTM 深度解析：从门控机制到实际应用

news 2025/9/15 6:47:18

LSTM介绍

在深度学习领域，循环神经网络 (RNN) 是处理序列数据的强大工具，但传统 RNN 在处理长序列时面临两个主要挑战：短时记忆和梯度消失 / 爆炸问题。当序列长度增加时，RNN 很难捕捉到序列中相隔较远的信息之间的依赖关系，这种现象被称为 "记忆健忘症"。同时，在反向传播过程中，梯度会随着时间步的推移而逐渐消失或爆炸，导致模型难以学习到长期依赖关系。

LSTM（Long Short-Term Memory，长短期记忆网络）的诞生正是为了解决这些问题。它通过引入记忆单元和门控机制，能够有效地处理长期依赖信息，在自然语言处理、语音识别、时间序列预测等诸多领域取得了巨大的成功。与传统 RNN 相比，LSTM 在梯度保持能力、长序列建模精度和训练收敛速度等方面都有显著提升。

LSTM 核心架构与原理

细胞状态：信息传递的高速公路

LSTM 的核心是细胞状态(Cell State)，它就像一条贯穿 LSTM 单元的 “信息高速公路”，可以在序列的处理过程中长时间地保存和传递信息。细胞状态可以选择性地更新和遗忘信息，从而实现对长期依赖的建模。

与传统 RNN 不同，LSTM 中的信息传递主要通过细胞状态而非隐藏状态进行，这使得重要信息能够在不受干扰的情况下传递，有效避免了梯度消失问题。

三大智能门控系统

LSTM 通过三个门控机制来控制信息的流动：遗忘门、输入门和输出门。这些门控机制使用 sigmoid 激活函数，输出 0 到 1 之间的值，表示信息通过的比例。

门控类型	功能类比	数学表达式	物理意义
遗忘门	智能记忆过滤器		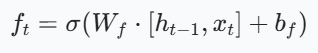决定从细胞状态中丢弃哪些信息
输入门	新知融合系统	$(i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i))$	决定将哪些新信息添加到细胞状态中
输出门	信息蒸馏器		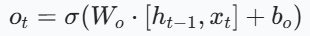决定细胞状态的哪些部分将作为当前时刻的输出

其中:σ表示 sigmoid 函数，它将值压缩在 0 和 1 之间，类似于 "门开合的大小程度"

记忆更新过程详解

LSTM 的记忆更新过程可以分为以下几个步骤：

遗忘门操作： 根据当前输入和上一时刻的隐藏状态，计算遗忘门的值f_t，决定从细胞状态中丢弃哪些信息。
输入门操作： 计算输入门的值i_t，决定将哪些新信息添加到细胞状态中。同时，生成候选值C~t，用于更新细胞状态。
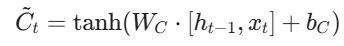
细胞状态更新： 根据遗忘门和输入门的输出，更新细胞状态。
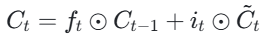
输出门操作： 计算输出门的值o_t，并根据更新后的细胞状态生成当前时刻的隐藏状态。

这个过程可以理解为：遗忘门决定丢弃过去的多少信息，输入门决定添加多少新信息，输出门决定输出多少当前信息。通过这种机制，LSTM 能够选择性地记住或忘记信息，从而实现对长期依赖的建模。

LSTM 如何缓解梯度消失问题？

LSTM 缓解梯度消失问题的关键在于其细胞状态的直接传递路径。当遗忘门f_t处于闭合状态（值接近 1）时，细胞状态C_t的梯度可以直接沿着最下面这条短路线传递到C_t−1，不受参数W的影响。

这使得梯度在反向传播时能够更有效地在时间序列中传递，避免了梯度消失或爆炸问题。相比之下，传统 RNN 的梯度在反向传播时需要反复乘以参数矩阵，容易导致梯度消失或爆炸。LSTM 通过这种 “短路连接” 机制，使得梯度能够在更长的序列中保持有效，从而更好地学习长期依赖关系。

LSTM 变体：双向 LSTM 和 GRU

双向 LSTM (BiLSTM)

传统的 LSTM 只能从前向后处理序列，而双向 LSTM(Bidirectional LSTM) 通过同时运行两个 LSTM 来克服这一限制：一个按照序列的正向顺序处理数据，另一个按照反向顺序处理数据。

双向 LSTM 的结构与原理

BiLSTM 的结构非常直观：它由两个单向 LSTM 层组成，一个是正向 LSTM，从序列的开始到结束逐步处理数据；另一个是反向 LSTM，从序列的结束到开始进行处理。在每个时间步，BiLSTM 将正向隐藏状态和反向隐藏状态进行拼接或其他融合操作，得到该时间步的最终隐藏状态表示。

这种结构使得 BiLSTM 能够同时获取序列中每个元素的前后文信息，从而更全面地捕捉序列的特征和上下文关系。在处理自然语言文本等序列数据时，一个词或短语的含义往往依赖于其周围的上下文，BiLSTM 通过融合前后向信息，能够更好地理解每个位置的上下文。

门控循环单元 (GRU)

门控循环单元(Gated Recurrent Unit, GRU) 是 LSTM 的一种简化版本，它将两个门 (输入门和遗忘门) 合并为一个门，称为更新门。GRU 由 Cho 等人于 2014 年提出，在许多应用中表现出与 LSTM 相当甚至更优的性能。

GRU 的结构与原理

GRU 的结构比 LSTM 更简单，主要包含两个门：

更新门(Update Gate)：决定丢弃哪些旧信息，添加哪些新信息。它将 LSTM 中的输入门和遗忘门合并为一个门。
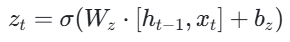
重置门(Reset Gate)：控制前一时刻隐层单元h_ t−1对当前词x_t的影响。

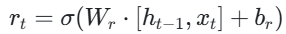
GRU 的工作原理如下：

计算更新门z_t和重置门r_t的值
根据重置门的值计算候选隐藏状态h_t
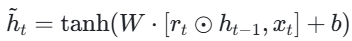
根据更新门的值更新隐藏状态

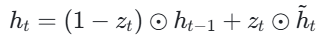
当更新门z_t接近 0 时，GRU 会忽略当前输入，直接传递前一时刻的隐藏状态，这构成了从h_t−1到h_t的 “短路连接”，有效缓解了梯度消失现象。

LSTM 与 GRU 的对比

虽然 GRU 的结构更加简洁，但它在许多应用中表现出与 LSTM 相当的性能，在某些情况下甚至更优。两者的主要区别在于：

特性	LSTM	GRU
门控机制	三个门 (输入门、遗忘门、输出门)	两个门 (更新门、重置门)
记忆载体	使用记忆单元 (Cell State)	直接使用隐藏状态
结构复杂度	较高	较低
计算效率	较低	较高
参数数量	较多	较少

GRU 的优点包括结构简化、计算效率高、参数数量少，因此在某些场景下训练速度更快。LSTM 的优点是能够更灵活地控制信息的流动，可能更适合处理复杂的序列数据。

在实际应用中，两者的选择通常取决于具体任务和资源限制。虽然 GRU 的结构更简单，但在许多情况下，它与 LSTM 的性能差异并不显著。

LSTM 实现与代码示例

在 PyTorch 中，LSTM 的实现非常简洁。PyTorch 提供了torch.nn.LSTM类，我们可以通过简单的代码构建 LSTM 模型。

import torch
import torch.nn as nn# 定义LSTM模型
class LSTMModel(nn.Module):def __init__(self, input_size, hidden_size, num_layers):super().__init__()self.lstm = nn.LSTM(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers,batch_first=True)self.fc = nn.Linear(hidden_size, 1)  # 全连接层用于输出def forward(self, x):# x形状: (batch_size, seq_len, input_size)out, _ = self.lstm(x)  # out形状: (batch_size, seq_len, hidden_size)out = self.fc(out[:, -1, :])  # 取最后一个时间步的输出return out# 参数设置
input_size = 8  # 输入特征维度，如包含开盘价、收盘价等8个特征
hidden_size = 64  # 隐层维度
num_layers = 3  # 三层堆叠结构# 实例化模型
model = LSTMModel(input_size, hidden_size, num_layers)# 示例输入
batch_size = 32
seq_len = 10
x = torch.randn(batch_size, seq_len, input_size)
output = model(x)
print(output.shape)  # 输出形状: (32, 1)