当前位置：首页 > news >正文

代码随想录二刷之“动态规划”～GO

news 2025/9/13 9:07:56

动规五部曲分别为：

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

基础题目

1.509. 斐波那契数 - 力扣（LeetCode）

func fib(n int) int {if n < 2{return n}pre,cur := 0,1for i := 2;i<=n;i++{next := pre + curpre = curcur = next}return cur
}

感悟：最开始想开数组了，然后发现挺多余的

2.70. 爬楼梯 - 力扣（LeetCode）

func climbStairs(n int) int {if n == 1{return n}dp := make([]int,n+1)dp[1] = 1dp[2] = 2for i:= 3;i<=n;i++{dp[i] = dp[i-1]+dp[i-2]}return dp[n]
}

感悟：弱智

3.746. 使用最小花费爬楼梯 - 力扣（LeetCode）

func minCostClimbingStairs(cost []int) int {if len(cost) == 1{return cost[0]}dp := make([]int,len(cost)+1)//到达i层的花费dp[0] = 0dp[1] = 0dp[2] = min(cost[0],cost[1])for i := 3;i<=len(cost);i++{dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])}return dp[len(cost)]
}
func min(i,j int)int{if i < j{return i}else{return j}
}

感悟：没有上一题弱智

4.62. 不同路径 - 力扣（LeetCode）

func uniquePaths(m int, n int) int {dp := make([][]int,m)for i := range dp{dp[i] = make([]int,n)dp[i][0] = 1}for j := 0;j < n;j++{dp[0][j] = 1}for i := 1;i < m;i++{for j := 1;j < n;j++{dp[i][j] = dp[i-1][j] + dp[i][j - 1]}}return dp[m-1][n-1]
}

感悟：个人感觉依旧挺弱智

5.63. 不同路径 II - 力扣（LeetCode）

func uniquePathsWithObstacles(obstacleGrid [][]int) int {m, n := len(obstacleGrid), len(obstacleGrid[0])//如果在起点或终点出现了障碍，直接返回0if obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1 {return 0}dp := make([][]int, m)for i, _ := range dp {dp[i] = make([]int, n)}// 初始化, 如果是障碍物, 后面的就都是0, 不用循环了for i := 0; i < m && obstacleGrid[i][0] == 0; i++ {dp[i][0] = 1}for i := 0; i < n && obstacleGrid[0][i] == 0; i++ {dp[0][i] = 1}for i := 1; i < m; i++ {for j := 1; j < n; j++ {if obstacleGrid[i][j] != 1 {dp[i][j] = dp[i-1][j] + dp[i][j-1]}}}return dp[m-1][n-1]
}

感悟：上道题一样弱智，只不过多了个障碍物

6.343. 整数拆分 - 力扣（LeetCode）

func integerBreak(n int) int {dp := make([]int,n+1)dp[1] = 1dp[2] = 1for i := 3;i <= n;i++{for j := 1;j < i;j++{dp[i] = max(dp[i],max((i-j)*j,(i-j)*dp[j]))}}return dp[n] 
}
func max(a, b int) int{if a > b {return a}return b
}

感悟：这道题以前都做过两遍了，这次居然又犯了相同的错误。

//贪心（数学归纳法证明）
对于整数 n > 4，将其拆分为尽可能多的3，能使乘积最大化。
func integerBreak(n int) int {if n == 2 {return 1}if n == 3 {return 2}if n == 4 {return 4}result := 1for n > 4 {result *= 3n -= 3}result *= nreturn result
}

7.96. 不同的二叉搜索树 - 力扣（LeetCode）

func numTrees(n int) int {if n == 1{return 1}dp := make([]int,n+1)//二叉搜索树个数dp[0] = 1dp[1] = 1for i := 2;i <= n;i++{for j := 1;j<=i;j++{dp[i] += dp[i-j]*dp[j-1]}}return dp[n]
}

感悟：这道题刚才又卡顿了，但是观察之后，就发现了递推公式。

背包问题

1.0-1背包问题46. 携带研究材料（第六期模拟笔试）

我觉得先遍历物品比较容易

package mainimport ("fmt"
)func main() {var m,n int//m表示物品种类，n表示行李空间fmt.Scan(&m,&n)weight := make([]int,m)value := make([]int,m)for i := 0;i < m;i++{fmt.Scan(&weight[i])}for i := 0;i < m;i++{fmt.Scan(&value[i])}dp := make([][]int,m)//dp[i][j]表示能装j的情况下，选择0-i物品能产生的最大价值for i := range dp{dp[i] = make([]int,n+1)}for i := weight[0];i <= n;i++{dp[0][i] = value[0]}for i := 1;i < m;i++{for j := 0;j <= n;j++{if j < weight[i]{dp[i][j] = dp[i-1][j]}else{dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])}}} fmt.Println(dp[m-1][n])
}func max(x, y int) int {if x > y {return x}return y
}

感悟：背包问题其实很好敲，就是边界问题，比如初始化的时候加不加1，写for循环条件的时候有没有等于，这种小细节。还有就是初始化的小小细节。

func main() {var m,n int//m表示物品种类，n表示行李空间fmt.Scan(&m,&n)weight := make([]int,m)value := make([]int,m)for i := 0;i < m;i++{fmt.Scan(&weight[i])}for i := 0;i < m;i++{fmt.Scan(&value[i])}dp := make([]int,n+1)//滚动数组//装j个物体的最大价值for i := 0;i < m;i++{for j := n;j >= weight[i];j--{dp[j] = max(dp[j],dp[j-weight[i]]+value[i])}}fmt.Println(dp[n])
}func max(x, y int) int {if x > y {return x}return y
}

感悟：滚动数组不需要初始化，是因为不像是二维数组dp[i-1][j]这种，数组不会越界，本身就是从0开始遍历。

2.416. 分割等和子集 - 力扣（LeetCode）

但当 "重量=价值" 时，意味着：

每个物品的重量就是它的价值
我们想要在不超过背包容量的前提下，最大化装入物品的总重量

func canPartition(nums []int) bool {sum := 0for _,num := range nums{sum += num}if sum % 2 == 1{return false}target := sum/2dp := make([]int,target + 1)//dp[i]表示，装重量为i的物品所能装的最多数量for i := 0; i < len(nums);i++{for j := target;j>=nums[i];j--{dp[j] =  max(dp[j],dp[j-nums[i]]+nums[i])}}return dp[target] == target
}

感悟：这道题其实印象挺深刻的，因为前几天和XZR battle过。当时我的思路是排序（本题不是必须的）然后回溯（因为当时刚复习完回溯，很深刻）下面是回溯法示例，但是超时了

func canPartition(nums []int) bool {sum := 0for _,num := range nums{sum += num}if sum % 2 == 1{return false}target := sum/2var backtrack func(start,currentSum int)boolbacktrack = func(start,currentSum int)bool{if currentSum == target{return true}if currentSum > target{return false}for i := start;i < len(nums);i++{if backtrack(i+1,currentSum + nums[i]) == true{return true}}return false}return backtrack(0, 0)
}

3.1049. 最后一块石头的重量 II - 力扣（LeetCode）

func lastStoneWeightII(stones []int) int {sum := 0for _, v := range stones {sum += v}target := sum / 2dp := make([]int,target+1)//背包容量为target的情况下，能装下的最多石头重量for i := 0; i < len(stones); i++ {for j := target; j >= stones[i]; j-- {dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])}}return sum - 2 * dp[target]
}func max(a, b int) int {if a > b {return a}return b
}

感悟：这道题最开始没发现他和分割等和子集很类似，但后来发现无非就是将石头分成两堆，使两堆的重量差最小。比如一堆是dp[target]，另一堆是sum-dp[target]。做差得：sum-2*dp[target]

4.494. 目标和 - 力扣（LeetCode）

感悟：二刷依旧没做出来，但是回溯可以。

func findTargetSumWays(nums []int, target int) int {result := 0var backtracking func(start int, currentSum int)backtracking = func(start int, currentSum int) {if start == len(nums) {if currentSum == target {result++}return  // 必须返回，否则会继续执行下面的递归！}backtracking(start+1,currentSum+nums[start])backtracking(start+1,currentSum-nums[start])}backtracking(0, 0)return result
}

假设加法的总和为x，那么减法对应的总和就是sum - x
所以我们要求的是x - (sum - x) = target
x = (target + sum) / 2

func findTargetSumWays(nums []int, target int) int {sum := 0//加 x,减 sum -x//x - (sum - x) = target//target = 2*x-sumfor _,v := range nums{sum += v}if abs(target) > sum || (sum+target)%2 == 1{return 0}bag := (sum + target) / 2dp := make([]int, bag+1)//背包容量为j的时候，可以装的最多种类数dp[0] = 1for i := 0; i < len(nums); i++ {for j := bag; j >= nums[i]; j-- {dp[j] += dp[j-nums[i]]}}return dp[bag]
}func abs(x int) int {return int(math.Abs(float64(x)))
}

5.474. 一和零 - 力扣（LeetCode）

func findMaxForm(strs []string, m int, n int) int {dp := make([][]int,m+1)for i,_ :=range dp{dp[i] = make([]int,n+1)}//最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。for i := 0; i < len(strs); i++ {// 对每个字符串统计0和1的个数zero := strings.Count(strs[i], "0")one := len(strs[i]) - zero// 从后向前遍历背包容量for j := m; j >= zero; j-- {for k := n; k >= one; k-- { dp[j][k] = max(dp[j][k], dp[j-zero][k-one] + 1)}}}return dp[m][n]
}func max(a,b int) int {if a > b {return a}return b
}

感悟：就是这道题的思路我好难思考啊，第一个难点：逐字符判断，

每个字符串处理时，都会更新所有相关的容量状态
dp[j][k] 记录的是历史最优解
从后向前遍历保证每个字符串只被使用一次

6.完全背包52. 携带研究材料（第七期模拟笔试）

package main
import "fmt"func main(){//n表示物品种类，v表示背包容量var n, v intfmt.Scan(&n, &v)weight := make([]int,n+1)value := make([]int,n+1)for i := 1; i <= n; i++ {fmt.Scan(&weight[i], &value[i])}dp := make([]int,v+1)//dp[j]表示容量为j的时候最大价值for i := 1;i <= n;i++{//物品种类for j := weight[i];j<=v;j++{//容量dp[j] = max(dp[j],dp[j-weight[i]] + value[i])}}fmt.Println(dp[v])
}func max(a, b int) int {if a > b {return a}return b
}

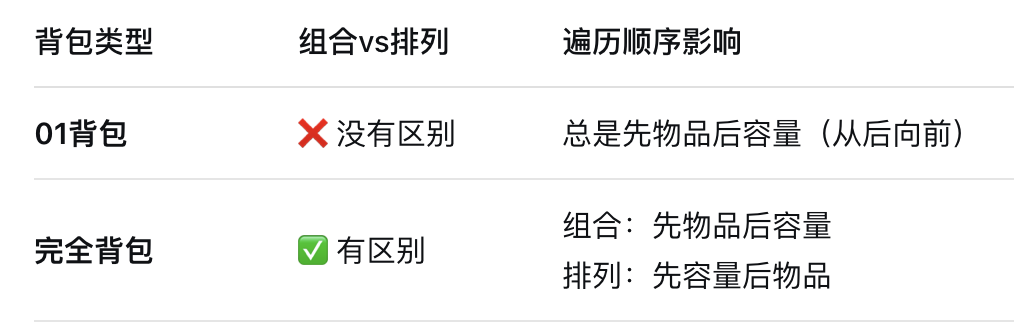
感悟：0-1背包与完全背包的区别，我个人感觉就是遍历顺序吧。以外层遍历是遍历背包为例，

8.377. 组合总和 Ⅳ - 力扣（LeetCode）

func combinationSum4(nums []int, target int) int {//定义dp数组dp := make([]int, target+1)// 初始化dp[0] = 1// 遍历顺序, 先遍历背包,再循环遍历物品for j:=0;j<=target;j++ {for i:=0 ;i < len(nums);i++ {if j >= nums[i] {dp[j] += dp[j-nums[i]]}}}return dp[target]
}

9.爬楼梯进阶版 57. 爬楼梯（第八期模拟笔试）

package mainimport "fmt"func climbStairs(n int, m int) int {dp := make([]int, n+1)dp[0] = 1for i := 1; i <= n; i++ {for j := 1; j <= m; j++ {if i-j >= 0 {dp[i] += dp[i-j]}}}return dp[n]
}func main() {var n, m intfmt.Scan(&n, &m)result := climbStairs(n, m)fmt.Println(result)
}

感悟：没什么难度，只需要能判断出它是完全背包问题，是排列问题还是组合问题，最后要求得是极值问题还是求方法数/组合数问题

10.322. 零钱兑换 - 力扣（LeetCode）

感悟：就是很普通的完全背包问题，记住完全背包模板，同时分辨好下面的那些情况就OK。一刷的时候犯的问题：dp[j] = max(dp[j],dp[j-coins[i]]+1)递推公式写错了，我写的这个

func change(amount int, coins []int) int {dp := make([]int,amount+1)//dp[i]表示，达到amount的时候的凑成金额的方式数量dp[0] = 1for i := 0;i < len(coins);i++{for j := coins[i];j <= amount;j++{dp[j] += dp[j-coins[i]]}}return dp[amount]
}

11.279.完全平方数

感悟：这道题比较基础，只不过最开始最外层不小心初始化成0了。。。。😭

func numSquares(n int) int {dp := make([]int,n+1)for i := 1; i <= n; i++ {dp[i] = math.MaxInt32}dp[0] = 0for i := 1;i <= n;i++{for j := 1;j * j <= i;j++{dp[i] = min(dp[i],dp[i - j * j]+1)}}return dp[n]
}

12.139.单词拆分

看到这个题就应该联想到回溯那一章敲过的分割IP地址那个题，也就是说遍历切割点。所以这个

func wordBreak(s string, wordDict []string) bool {n := len(s)// dp[i] 表示 s[0:i] 能否被拆分为字典中的单词dp := make([]bool, n+1)dp[0] = true // 空字符串可以被拆分wordDictset := make(map[string]bool)for _,v := range wordDict{wordDictset[v] = true}for i := 1;i <= n;i++{for j := 0;j < i;j++{//j表示分割点if dp[j] && wordDictset[s[j:i]]{dp[i] = truebreak}}}return dp[n]
}

dp[i] 表示字符串 s 的前 i 个字符能否被拆分为字典中的单词
初始化 dp[0] = true（空字符串可以被拆分）
对于每个位置 i，检查所有可能的分割点 j（0 ≤ j < i）
如果 dp[j] 为真且子串 s[j:i] 在字典中，则 dp[i] 为真
最终返回 dp[n]，其中 n 是字符串长度

13.总结

问能否能装满背包（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

动态规划：416.分割等和子集(opens new window)
动态规划：1049.最后一块石头的重量 II(opens new window)

问装满背包有几种方法：dp[j] += dp[j - nums[i]] ，对应题目如下：

动态规划：494.目标和(opens new window)
动态规划：518. 零钱兑换 II(opens new window)
动态规划：377.组合总和Ⅳ(opens new window)
动态规划：70. 爬楼梯进阶版（完全背包）(opens new window)

问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

动态规划：474.一和零(opens new window)

问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

动态规划：322.零钱兑换(opens new window)
动态规划：279.完全平方数

无论循环顺序如何，dp[] 的索引永远代表的是容量/目标值

打家劫舍

1.198.打家劫舍

func rob(nums []int) int {dp := make([]int,len(nums)+1)//dp[i]表示偷盗到i号房屋的时候，获得的最大金额dp[1] = nums[0]for i := 2;i <= len(nums);i++{dp[i] = max(dp[i-1],dp[i-2]+nums[i-1])}return dp[len(nums)]
}

感悟：一点不难，就是注意索引是否越界

2.213.打家劫舍2️⃣

感悟：这道题二刷时候的思路有点点忘了，所以首先考虑不偷第一个房子，然后考虑不偷最后一个房子。因为首尾房子是相连的（环形），其中不偷首尾的房子上面两种情况已经包括了

func rob(nums []int) int {n := len(nums)if n == 0 {return 0}if n == 1 {return nums[0]}result1 := robLinear(nums[1:])//偷最后一间房result2 := robLinear(nums[:n-1])//不偷最后一间房return max(result1, result2)
}func robLinear(nums []int) int {n := len(nums)if n == 0 {return 0}if n == 1 {return nums[0]}dp := make([]int, n)dp[0] = nums[0]dp[1] = max(nums[0], nums[1])for i := 2; i < n; i++ {dp[i] = max(dp[i-1], dp[i-2] + nums[i])}return dp[n-1]
}

3.337.打家劫舍3️⃣

感悟：取父节点或者不取父节点两种情况，然后分别取最大值.[树形dp]

func rob(root *TreeNode) int {if root == nil{return 0}if root.Left == nil && root.Right == nil{return root.Val}val1 := root.Val//偷父节点if root.Left != nil{val1 += rob(root.Left.Left)+rob(root.Left.Right)}if root.Right != nil{val1 += rob(root.Right.Right)+rob(root.Right.Left)}val2 := rob(root.Left)+rob(root.Right)return max(val1,val2)
}

方法二：在暴力基础上使用记忆化递归

func rob(root *TreeNode) int {set := make(map[*TreeNode]int)return dfs(root, set)
}func dfs(root *TreeNode, set map[*TreeNode]int) int {if root == nil {return 0}if val, exists := set[root]; exists {return val}val1 := root.Valif root.Left != nil {val1 += dfs(root.Left.Left, set) + dfs(root.Left.Right, set)}if root.Right != nil {val1 += dfs(root.Right.Left, set) + dfs(root.Right.Right, set)}val2 := dfs(root.Left, set) + dfs(root.Right, set)result := max(val1, val2)set[root] = resultreturn result
}func max(a, b int) int {if a > b {return a}return b
}

方法三：状态dp

func rob(root *TreeNode) int {if root == nil{return 0}var dfs func(root *TreeNode)[2]intdfs = func(root *TreeNode)[2]int{if root == nil{return [2]int{0,0}}left := dfs(root.Left)right := dfs(root.Right)v1 := root.Val + left[0] + right[0]//取根节点。1v2 := max(left[0],left[1]) + max(right[0],right[1])// 0return [2]int{v2, v1}}result := dfs(root)return max(result[0],result[1])
}
func max(a, b int) int {if a > b {return a}return b
}

股票问题

1.121. 买卖股票的最佳时机

只能买一张

对于递推公式：dp[i][1]，某一天持有股票，可以有前一天持有股票（如果有），以及如果那一天正好第一次买入股票，即-prices[i]。因为只能买一支股票。如果可以买多张，那么dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])(如果不是-prices[i]，说明有可能不是第一次买。但如果是 -prices[i]限制了只能买一次)

func maxProfit(prices []int) int {//只能买一支股票if len(prices) == 0{return 0}sum := 0min := prices[0]for i := 1;i<len(prices);i++{profit := prices[i] - minif profit > sum{//更新最大收益sum = profit}if prices[i] < min{min = prices[i]//寻找买入价格最低点,去求利润最大点}}return sum
}func maxProfit(prices []int) int {if len(prices) == 0{return 0}dp := make([][]int,len(prices))for i := 0; i < len(prices); i++ {dp[i] = make([]int, 2)}dp[0][0] = 0dp[0][1] = -prices[0]for i := 1; i < len(prices); i++ {dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])dp[i][1] = max(dp[i-1][1], -prices[i])}return dp[len(prices)-1][0]
}

2.122. 买卖股票的最佳时机 II

允许同一天买卖

func maxProfit(prices []int) int {if len(prices) == 0 {return 0}dp := make([][]int,len(prices))for i := 0;i < len(prices);i++{dp[i] = make([]int,2)}//dp[i][0]表示第i天不持有股票的最大收益//dp[i][1]表示第i天持有股票的最大收益dp[0][0] = 0dp[0][1] = -prices[0]for i := 1;i < len(prices);i++{dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i])dp[i][1] = max(dp[i-1][1],dp[i-1][0] - prices[i])}return dp[len(prices)-1][0]
}

3.123. 买卖股票的最佳时机 III

感悟：一刷的时候已经很熟练了

func maxProfit(prices []int) int {if len(prices) == 0{return 0}dp := make([][]int,len(prices))for i := 0;i<len(prices);i++{dp[i] = make([]int,4)}dp[0][0] = -prices[0]dp[0][1] = 0dp[0][2] = -prices[0]dp[0][3] = 0for i := 1;i < len(prices);i++{dp[i][0] = max(dp[i-1][0],-prices[i])dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i])dp[i][2] = max(dp[i-1][2],dp[i-1][1]-prices[i])dp[i][3] = max(dp[i-1][3],dp[i-1][2]+prices[i])}//dp[i][0]表示第i天第一次买入,dp[i][1]表示第i天第一次卖出//dp[i][2]表示第i天第二次买入,dp[i][3]表示第i天第二次卖出return max(dp[len(prices)-1][3],dp[len(prices)-1][1])
}

4.188. 买卖股票的最佳时机 IV

感悟：只不过在上面那个题的基础之上引入了k（若干次买入卖出）

func maxProfit(k int, prices []int) int {if k == 0 || len(prices) == 0 {return 0}dp := make([][]int, len(prices))for i := range dp {dp[i] = make([]int,2*k+1)}for j := 1; j < 2 * k; j += 2 {dp[0][j] = -prices[0]}for i := 1; i < len(prices); i++ {for j := 0; j < 2 * k; j += 2 {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i])dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i])}}return dp[len(prices) - 1][2 * k]
}

5.309. 买卖股票的最佳时机含冷冻期

感悟：这道题也很简单，我觉得不难

func maxProfit(prices []int) int {if len(prices) == 1{return 0}dp := make([][]int,len(prices))for i := range dp{dp[i] = make([]int,3)}dp[0][0] = -prices[0]dp[0][1] = 0//0 买入，1卖出，2冷冻期for i := 1;i < len(prices);i++{dp[i][0] = max(dp[i-1][0],dp[i-1][2] - prices[i])dp[i][1] = max(dp[i-1][1],dp[i-1][0] + prices[i])dp[i][2] = max(dp[i-1][2],dp[i-1][1])}return max(dp[len(prices)-1][1],dp[len(prices)-1][2])
}

6.714. 买卖股票的最佳时机含手续费

func maxProfit(prices []int, fee int) int {dp := make([][2]int,len(prices))dp[0][0] = -prices[0]for i := 1;i<len(prices);i++{dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i])dp[i][1] = max(dp[i-1][1],dp[i-1][0] + prices[i] - fee)}return dp[len(prices)-1][1]
}

感悟：股票问题都很基础，感觉以后不用刷了

子序列问题

子序列不一定连续（比如做前面数组的题经常性的一位子序列是连续的）

还要明确dp数组的含义，即处理完前 i 个元素、前 j 个元素后的全局最优解，才返回dp[i][j]。如果题干的意思，你能发现最优解可能在不用处理到最后之前就能找到的，这个时候dp数组含义就是以nums[i]结尾的最长递增子序列。！！！🙌🏼

子序列（不连续）

1.300. 最长递增子序列

方法一：动态规划。递推公式刚才居然蒙住了😭🥵
dp[i]：以 nums[i] 结尾的最长递增子序列长度

func lengthOfLIS(nums []int) int {if len(nums) == 0{return 0}dp := make([]int,len(nums))//dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度for i := range dp{dp[i] = 1}res := 1for i := 1;i < len(nums);i++{for j := 0;j < i;j++{if nums[i] > nums[j]{dp[i] = max(dp[i],dp[j]+1)}}if dp[i] > res{res = dp[i]}}return res
}

方法二（优化）：贪心+二分

func lengthOfLIS(nums []int) int {if len(nums) == 0{return 0}dp := []int{}//dp的长度就是当前找到的最长递增子序列的长度//dp[i]表示每个长度子序列的最小尾部//只关心如何让尾部更小以支持未来扩展，不关心 dp 数组本身是否是实际 LISfor _,num := range nums{if len(dp) == 0 || dp[len(dp) - 1]  <  num{dp = append(dp,num)}else{l, r:= 0, len(dp) - 1for l <= r{mid := (r - l)/2 + lif dp[mid] >= num{r = mid - 1}else{l = mid + 1}}dp[l] = num}}return len(dp)
}

感悟：收获很大；首先明确了如果在for循环中定义的变量，作用于只有在for里面。二分查找也明确了一些，比如二分查找之后l一定是大于等于要查找的元素的。因为最后l > r终止循环，所以最后用dp[l]去承接num。最后本题的贪心思路很巧妙，即只关心如何让尾部更小，以支持未来的可扩展。dp[i]表示长度为len(dp)的时候，序列是以该元素结尾的。很巧妙！！同时降低了时间复杂度

2.1143. 最长公共子序列

func longestCommonSubsequence(text1 string, text2 string) int {dp := make([][]int,len(text1)+1)for i := range dp{dp[i] = make([]int,len(text2)+1)}for i := 1;i <= len(text1);i++{for j := 1;j <= len(text2);j++{if text1[i-1] == text2[j-1]{dp[i][j] = dp[i-1][j-1]+1}else{dp[i][j] = max(dp[i][j-1],dp[i-1][j])}}}return dp[len(text1)][len(text2)]
}

感悟：还好，不难，递推公式比较熟练了！！！然后递推公式还有一点感悟：即如果当前元素匹配不了的话，那么就把s或者t的尾元素删了（即dp[i-1][j],dp[j][i]）

3.1035. 不相交的线

func maxUncrossedLines(nums1 []int, nums2 []int) int {if len(nums1) == 0 || len(nums2) == 0{return 0}dp := make([][]int,len(nums1)+1)for i := range dp{dp[i] = make([]int,len(nums2)+1)}for i := 1;i <= len(nums1);i++{for j := 1;j <= len(nums2);j++{if nums1[i-1] == nums2[j-1]{dp[i][j] = dp[i-1][j-1] + 1}else{dp[i][j] = max(dp[i-1][j],dp[i][j-1])}}}return dp[len(nums1)][len(nums2)]
}

感悟：这道题就是最长公共子序列，一刷过二刷不难

子序列（连续）

1.674. 最长连续递增序列

动态规划，思路清晰，还好～🙃
dp[i]：以 nums[i] 结尾的最长递增子序列长度

func findLengthOfLCIS(nums []int) int {if len(nums) <= 1{return len(nums)}res := 1dp := make([]int,len(nums))for i := range dp{dp[i] = 1}for i := 1;i < len(nums);i++{if nums[i] > nums[i-1]{dp[i] = dp[i-1]+1}if dp[i] > res{res = dp[i]}}return res
}

2.718. 最长重复子数组

自己写的，就是些小细节，总导致无法AC。
dp[i][j] 表示 “以 nums1[i-1] 和 nums2[j-1] 结尾的最长公共连续子数组的长度”
举个例子A[0]如果和B[0]相同的话，dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0，正好符合递推公式逐步累加起来。因为dp从1开始遍历的！！！

func findLength(nums1 []int, nums2 []int) int {if len(nums1) == 0 || len(nums2) == 0{return 0}dp := make([][]int, len(nums1)+1)for i := range dp {dp[i] = make([]int, len(nums2)+1)}res := 0for i := 1;i <= len(nums1);i++{for j := 1;j <= len(nums2);j++{if nums1[i-1] == nums2[j-1]{dp[i][j] = dp[i-1][j-1]+1}if res < dp[i][j]{//这里也有贪心的思想，及时更新res  = dp[i][j]}}} return res
}

3.53. 最大子数组和

感悟：经过今天的训练之后，思路顺畅了

func maxSubArray(nums []int) int {if len(nums) == 0{return 0}res := nums[0]dp := make([]int,len(nums))//dp[i]表示，以nums[i]结尾的元素的连续子数组的最大和dp[0] = nums[0]for i := 1;i < len(nums);i++{/*if nums[i] + dp[i-1] < nums[i]{dp[i] = nums[i]}else{dp[i] = nums[i] + dp[i-1]}*/dp[i] = max(nums[i],nums[i]+dp[i-1])if dp[i] > res{res = dp[i]}}return res
}

编辑距离

1.392. 判断子序列

这个和最长公共子序列的区别是，这个判断是不是子序列，即dp[i][j]表示相同子序列的长度。

func isSubsequence(s string, t string) bool {dp := make([][]int,len(t)+1)for i := range dp{dp[i] = make([]int,len(s)+1)}//dp[i][j]表示以下标i-1为结尾的字符串t，和以下标j-1为结尾的字符串s，相同子序列的长度为dp[i][j]。for i := 1;i <= len(t);i++{for j := 1;j <= len(s);j++{if t[i-1] == s[j-1]{dp[i][j] = dp[i-1][j-1]+1}else{dp[i][j] = dp[i-1][j]}}} return dp[len(t)][len(s)] == len(s)
}

感悟：这道题递推公式的感悟，如果当前元素匹配，那么dp[i][j] = dp[i-1][j-1]+1。如果当前元素不匹配，那么可以把t尾元素删了（因为是在t里面找s,即dp[i-1][j]）。初始化的问题：某一个串为空，dp[i][j]都为0，因为根据定义来看，相同序列都为0.

2.115. 不同的子序列

（出现的个数）

func numDistinct(s string, t string) int {dp := make([][]int,len(s)+1)for i := range dp{dp[i] = make([]int,len(t)+1)dp[i][0] = 1//这里dp[i][0]，表示s的索引是i-1，t的索引是-1}//以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]//当t为空字符串时，所有s都有一个空子序列与之匹配，所以需要初始化dp[i][0] = 1。for i := 1;i <= len(s);i++{//在s里找tfor j := 1;j <= len(t);j++{if s[i-1] == t[j-1]{dp[i][j] = dp[i-1][j-1] + dp[i-1][j]}else{dp[i][j] = dp[i-1][j]}}}return dp[len(s)][len(t)]
}

感悟：这道题不太难，就是用s里面找t。如果s[i-1]==t[i-1]，dp[i][j] = dp[i-1][j-1]+dp[i-1][j](因为是s找t,所以比如bagg和bag。开始找s串的上一个元素了)。如果不相等。那么dp[i][j] = dp[i-1][j],状态就变成了s[i-2]和t[j-1]（因为是在s中找t）所以dp[i][j] = dp[i-1][j]。初始化问题：s为空的时候，再怎么说都不能变成t的，但是t为空的时候，s是有空串能和t匹配的。

3.583. 两个字符串的删除操作

func minDistance(word1 string, word2 string) int {dp := make([][]int,len(word1) + 1)for i := range dp{dp[i] = make([]int,len(word2) + 1)}for i := 1;i <= len(word1);i++{for j := 1;j <= len(word2);j++{if word1[i-1] == word2[j-1]{dp[i][j] = dp[i-1][j-1] + 1}else{dp[i][j] = max(dp[i-1][j],dp[i][j-1])}}}return len(word1) + len(word2) - 2 * dp[len(word1)][len(word2)]
}

感悟：我觉得蛮简单的，就是最长公共子序列的变种

4.72. 编辑距离

func minDistance(word1 string, word2 string) int {dp := make([][]int,len(word1)+1)for i := range dp {dp[i] = make([]int, len(word2)+1)}//word1变成word2的最小操作数for i := 0;i <= len(word1);i++{dp[i][0] = i//删除}for j := 0;j <= len(word2);j++{dp[0][j] = j//添加}for i := 1;i <= len(word1);i++{for j := 1;j <=len(word2);j++{if word1[i-1] == word2[j-1]{dp[i][j] = dp[i-1][j-1]}else{dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1}//替换、删除、（删除）}}return dp[len(word1)][len(word2)]
}

感悟：二刷刚开始的时候刷这个题是有点懵的，但是慢慢的发现，确定好递推公式之后其他的和子序列的思路都差不多。这里引用XZL的名言：多刷题，以后每道题的思路都是不一样的。所以不要去刻意对比某道题和某道题的递推公式为什么不一样

回文

1.647. 回文子串

func countSubstrings(s string) int {res := 0dp := make([][]bool,len(s))for i := range dp{dp[i] = make([]bool,len(s))}for i := len(s)-1;i>=0;i--{for j := i;j < len(s);j++{if s[i] == s[j]{if j - i <=1{res++dp[i][j] = true}else if dp[i+1][j-1]{res++dp[i][j] = true}}}}return res
}

感悟:

情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
情况二：下标i 与 j相差为1，例如aa，也是回文子串
情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
关于递推顺序的感悟：首先[i,j]，其次要看[i+1,j-1]所以，从左下到右上

2.516. 最长回文子序列

func longestPalindromeSubseq(s string) int {dp := make([][]int,len(s))for i := range dp{dp[i] = make([]int,len(s))dp[i][i] = 1}//dp[i][j]表示i到j范围内的最长回文序列长度for i := len(s)-1;i >= 0;i--{for j := i + 1;j < len(s);j++{//i==j的情况初始化的时候搞完了if s[i] == s[j]{dp[i][j] = dp[i+1][j-1] + 2}else{dp[i][j] = max(dp[i+1][j],dp[i][j-1])}}}return dp[0][len(s)-1]
}

感悟：本题的遍历顺序我觉得可以稍微背一下。首先根据回文，如果s[i] == s[j]的时候，i到j是否可以构成回文序列，完全取决于dp[i+1][j-1]是否是回文。所以相当于从dp[i+1][j-1]推到dp[i][j]。所以从左下推到右上。递推公式就可以顺理成章的写下来了。
本题和回文子串的区别：回文子串求个数，所以dp[i][j]是bool形，true一个，res就加一个。最后返回res。然后三种情况要记牢：a、aa、baab。然后左下到右上。而最长回文子序列求的是最长回文序列长度，所以dp[i][j]是int类型的。然后遍历顺序一样，递推公式也能顺理成章的写出来。然后刚才AC的时候，dp[i][j] = max(dp[i+1][j],dp[i][j-1])这里多写了一项，dp[i+1][j-1]，因为没必要，前两个已经包括了dp[i+1][j-1].