【java】常见排序算法详解

---

一.插入排序

插入排序一般分为两种： 1.直接插入排序 2.希尔排序

1.1 直接插入排序

对于一个数组，假设[arr[0],…,arr[i-1]]是排好序的，待排位置为arr[i]，从后往前依次和待排部分元素比较，直到找到待插入位置，之后将原位置及其后面的元素后移即可，之后不断重复即可；

代码示例：

public class InsertSort {public static void insertSort(int[] arr) {int i=0,j=0,tmp=0,n=arr.length;if(n==0||n==1) return ;for(i=1;i<n;i++) {//i位置为待插入元素tmp=arr[i];//tmp与[0,i-1]元素依次比较，且比较过程直接移动元素for(j=i-1;j>=0&&arr[j]>tmp;j--) {arr[j+1]=arr[j];}arr[j+1]=tmp;}}public static void main(String[] args) {int[] arr=new int[]{9,8,7,6,5,4,3,2,1};insertSort(arr);for(int x:arr) System.out.print(x+" ");}
}

直接插入排序的特点：

• 直接插入排序是一种稳定的排序算法
• 直接插入排序的数组越有序，排序效率越高
• 直接插入排序的时间复杂度为O(n^2),空间复杂度为O(1)

1.2 希尔排序

核心思路：

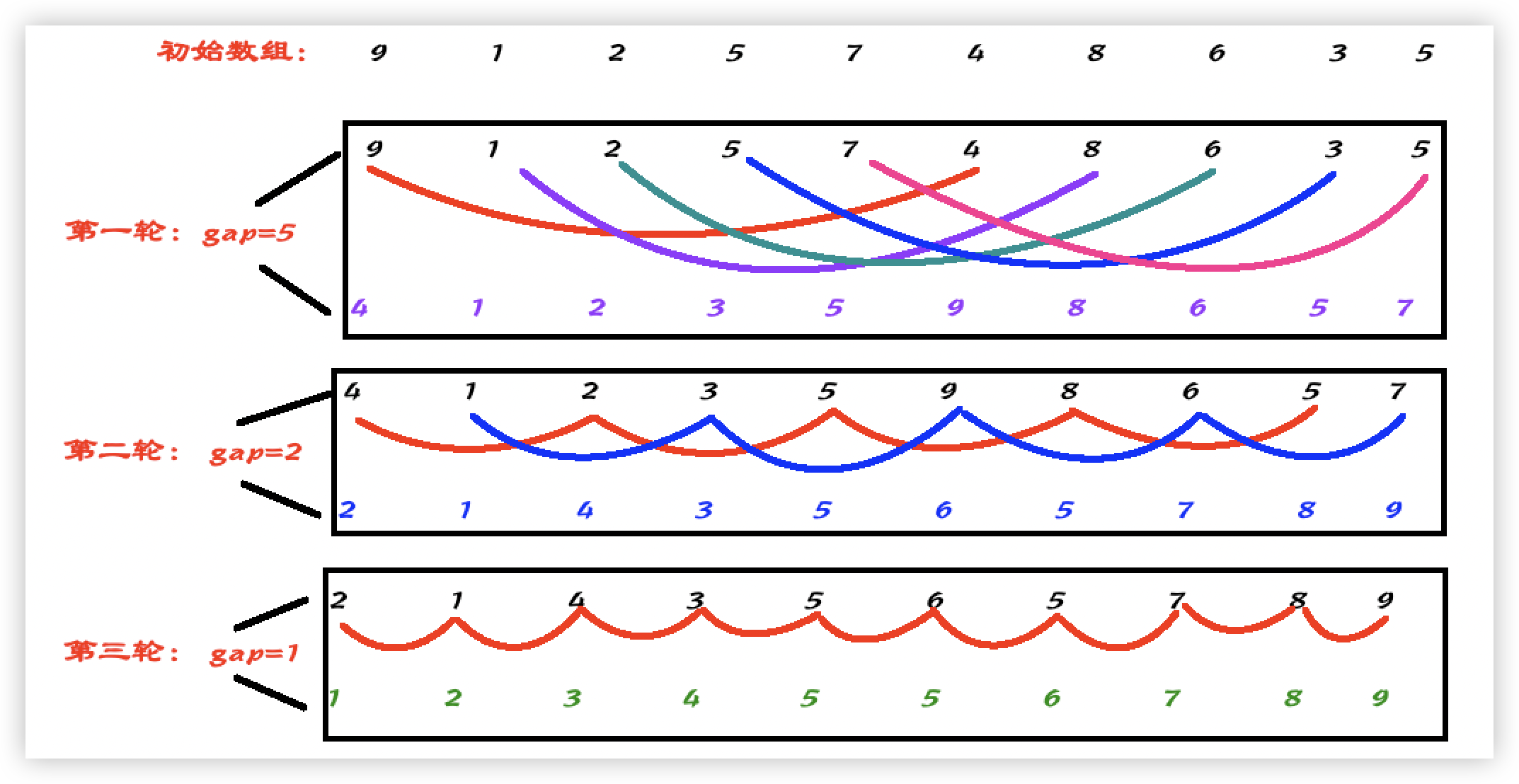
选取一个整数gap，将所有距离为gap的元素分为一组，对每个分组进行插入排序；
缩小gap的值，之后重新按照上述规则进行排序，直到gap=1停止排序；

public static void shell(int[] arr,int gap) {for(int i=gap;i<arr.length;i++) {	for(int j=i;j>=gap;j-=gap) {if(arr[j-gap]>arr[j]) {Swap.swap(arr, j-gap, j);}else {break;}}}
}public static void shellSort(int[] arr) {int gap=arr.length;while(gap>1) {gap/=2;shell(arr, gap);}
}public static void main(String[] args) {int[] arr=new int[]{9,8,7,6,5,4,3,2,1};shellSort(arr);for(int x:arr) System.out.print(x+" ");
}

希尔排序的特点：

• 希尔排序是对插入排序的优化，gap>1之前的排序是预排序，是为了让数组更接近有序
• 希尔排序的时间复杂度不好估计，因为gap的选择和更新策略有很多种，是不确定的；

二.选择排序

选择排序一般分为两种：1.选择排序 2.堆排序

2.1 选择排序

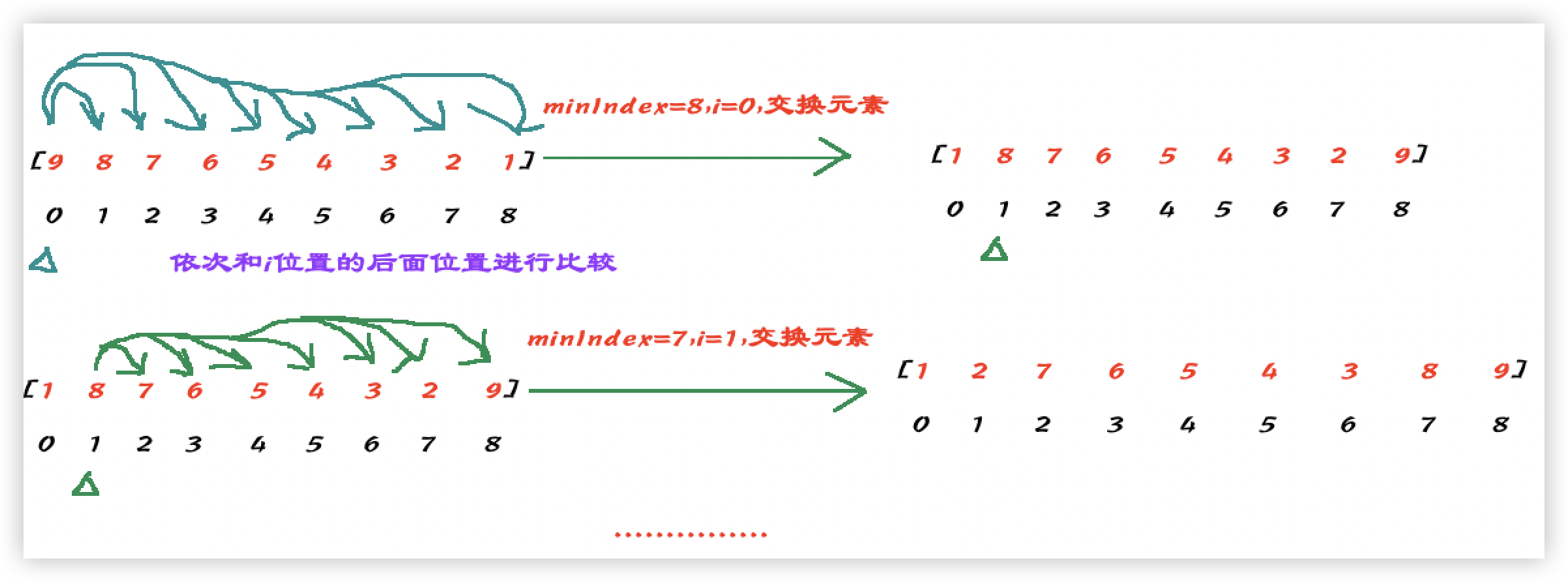
以升序为例，其基本思想为： 对于每个元素nums[i]，依次和其后面的元素进行比较，记录最小值所在下标index，交换i，index处的元素;

public class SelectSort {public static void selectSort(int[] arr) {//依次遍历每个元素for(int i=0;i<arr.length;i++) {int minIndex=i;//依次和后面的元素比较，获得最小值的indexfor(int j=i+1;j<arr.length;j++) {if(arr[minIndex]>arr[j]) {minIndex=j;					}}swap(arr, minIndex, i); //交换 i,index处的元素}}public static void main(String[] args) {int[] arr=new int[]{9,8,7,6,5,4,3,2,1};selectSort(arr);for(int x:arr) System.out.print(x+" ");}
}

选择排序的特点：

• 选择排序是不稳定的算法
• 选择排序的时间复杂度为O(n^2),空间复杂度为O(1)

2.2 堆排序

升序建大堆，降序建小堆；
堆排序的基本思路：

1. 首先建立一个空堆，之后依次插入数组元素，每次插入后调整堆，使其满足堆结构
2. 取出堆顶元素，堆最后一个元素代替堆顶，向下调整时满足堆结构;
3. 重复操作2，依次取出的元素即为已经排好序的序列；

public class HeapSort {public static void heapSort(int[] arr) {createHeap(arr);   //建大(小)堆int end=arr.length-1;while(end>0) {swap(arr, 0, end);   //堆顶，堆底元素互换shiftDown(arr,0, end); //向下调整end--;}}public static void createHeap(int[] array) {int size=array.length;for(int i=(size-1-1)/2;i>=0;i--) {shiftDown(array,i, size);  }}//i为要调整的位置//size为数组实际大小//向下调整的时间复杂度：O(logn)private static void shiftDown(int[] array,int i,int size) {int child=2*i+1;while(child<size) {  //只有节点有孩子就进循环//获取孩子节点最大值所在下标//1.如果无右孩子=》index=child   //2.有左右孩子  =》index=elem[child]<elem[child+1]?child+1:childint maxPos=(child+1<size)&&(array[child]<=array[child+1])?child+1:child;//如果已经是大根堆，则无需调整if(array[maxPos]<=array[i]) {break;}//节点交换，位置更新Swap.swap(array,i,maxPos);i=maxPos;child=2*i+1;}}public static void main(String[] args) {int[] arr=new int[]{1,9,7,6,0,5,3,8};heapSort(arr);for(int x:arr) System.out.print(x+" ");}
}   

三.交换排序

交换排序一般分为两种： 1.冒泡排序 2.快速排序

3.1 冒泡排序

每次将起点当作最值，依次和其他元素对比，如果不是最值，则两两交换，使得每次移动的都是最值，最终将最值放入末尾；之后循环此操作依次找出第k小的值；

public static void bubbleSort(int[] array) {int n=array.length;for(int i=0;i<n;i++) {boolean flag=false; //标记位，如果未发生交换，说明整体有序for(int j=0;j<n-i-1;j++) {if(array[j]>array[j+1]) {Swap.swap(array, j, j+1);flag=true;}}if(!flag==true) {break;}}}	  

3.2 快速排序

3.2.1 Hoare版

每次选择最左侧元素作为轴元素，右找小，左找大，最终找到轴元素的合适位置；

public static int partion3(int[] array,int l,int r) {int left=l,right=r;int ret=array[left];while(left<right) {//往右找小，找到停止while(left<right&&ret<=array[right]) {right--;}//往左找大，找到停止while(left<right&&ret>=array[left]) {left++;}//保证 左<轴元素<右 =》交换两个数据Swap.swap(array, left, right);}//l的位置即轴元素原来在的位置，交换位置Swap.swap(array, left, l);//返回轴元素的最终位置return left;
}
public static void quickSort3(int[] array,int l,int r) {if(l>=r) {return ;}//获取轴元素在排好序后的下标int index=partion3(array,l,r);//对轴元素的左侧继续取轴quickSort3(array,l,index-1);//对轴元素的右侧继续取轴quickSort3(array,index+1,r);
}

3.2.2 挖坑法

每次选取最左侧元素作为坑pivot,右找大，左找下，最终确定合适的坑的位置。

public static int partion(int[] array,int l,int r) {//每次选第一个元素作为坑int pivot=array[l];int left=l,right=r;while(left<right) {//必须加上left<right,因为不加可能即使left>right也不会停止//向右找比坑小的元素，找到停止并将小的放到left处while(left<right&&pivot<=array[right]) {right--;}//向右找比坑大的元素，找到停止并将大的放到right处array[left]=array[right];while(left<right&&pivot>=array[left]) {left++;}array[right]=array[left];}//全部找完,left即为坑的位置array[left]=pivot;//返回坑的位置return left;
}
public static void quickSort(int[] array,int l,int r) {if(l>=r) {return ;}int pivot=partion(array,l,r);//坑左边找新坑quickSort(array, l, pivot-1);//坑右边找新坑quickSort(array, pivot+1, r);
}

3.2.3 双指针法

一开始定义两个首位指针，首指针始终执行<x的边界，尾指针始终指向>x的边界；

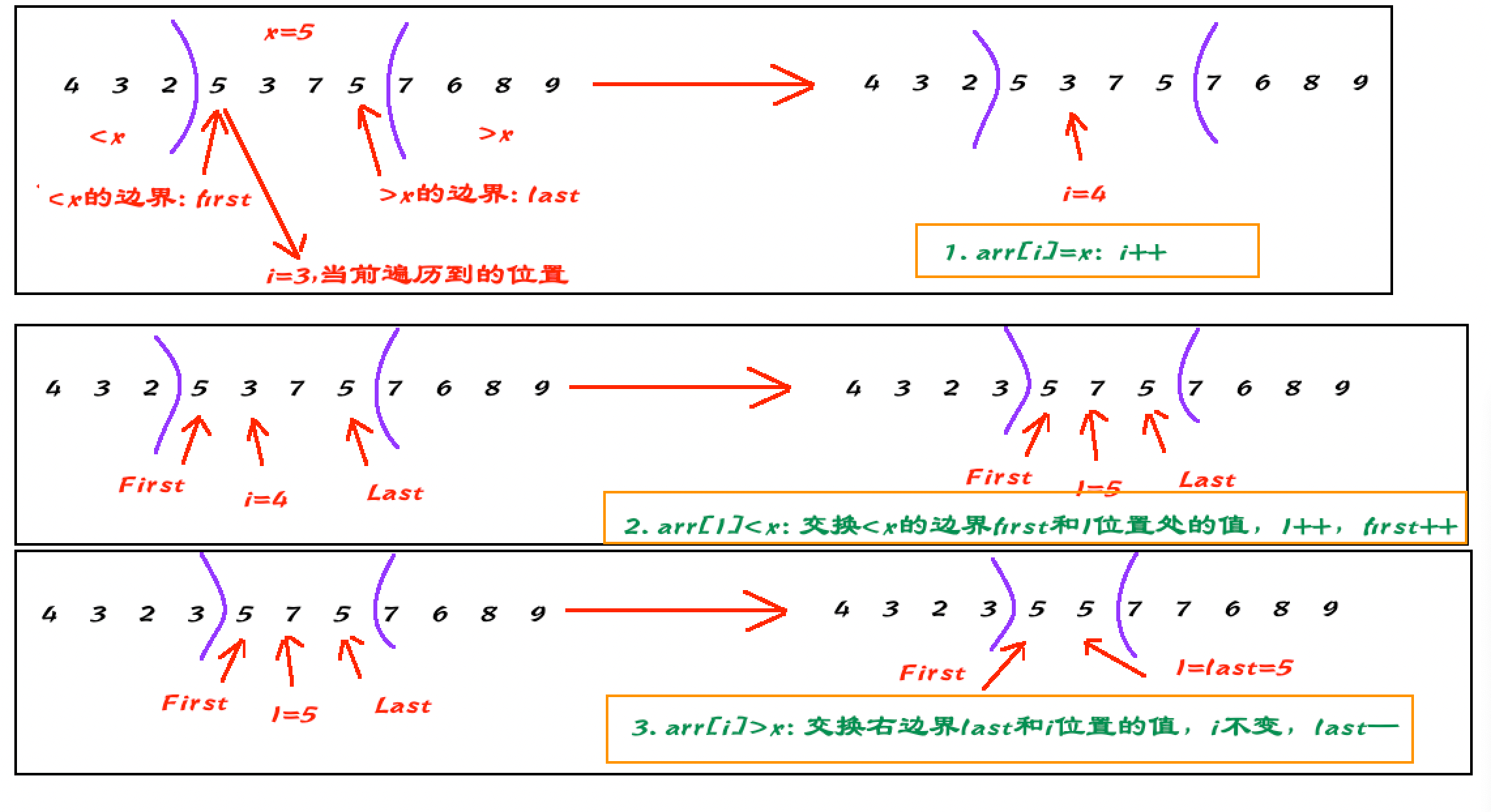
//first: <x的边界，即该处的值>=x
//last:  >x的边界，即该处的值<=x
//=>结合划分，最终一定有  arr[first]=arr[last]=x，且[first,last]表示均为x的部分
public static int first,last;
//对区间[l,r]内的元素进行划分，划分为三部分 <x   ==x    >x 并返回==x部分的位置
public static void partion1(int[] array,int l,int r,int target) {first=l;  //<x的边界last=r;   //>x的边界int i=l;while(i<=r&&i<=last) {//1.如果 arr[i]<x  => 交换i和first处的值，i++,first++;if(array[i]<target) {Swap.swap(array, first++, i++);}//2.如果 arr[i]>x  => 交换i和last处的值，last--,i不变，因为不知道//交换后的arr[i]的值属于哪部分else if(array[i]>target) {Swap.swap(array, last--, i);}//3.如果arr[i]==x  => i++else {i++;}}	
}
//递归过程本质是： 前序遍历(中左右)
public static void quickSort1(int[] array,int l,int r) {if(l>=r) {return ;}int x=array[l];  //选取第一个元素作为轴元素(可改进)//该函数结束，使得[l,r]分为三部分： 1.[l,first)<x  2.[first,last]=x 3.(last,r]>xpartion1(array,l,r,x);//防止全局变量被覆盖int left=first;int right=last;quickSort1(array,l,left-1);quickSort1(array,right+1,r);
}

快排本质就是： 二叉树的前序遍历

3.2.4 快排的优化

1.三数取中：
即每次从 left,right,(left+right)/2，三个位置中，选择这些位置对应值的中位数作为pivot;

2.小区间优化：
即便有三数取中，但这样的快排仍然有着问题。由上面的理论可知，快排实际就相当于二叉树的前序遍历，而树随着层的增高，其每层节点以指数形式上升，每个节点就是一次递归，因此可见，当区间越来越小，其时间消耗反而越来越多，因此，当区间小到一定层度时，改为其他的非递归排序，如插入排序；

3.随机快排：
如上的两种优化策略均无法实现真正的O(n * logn)的复杂度，但如果采用随机快排，即每次随机选取轴元素的策略，那么可以使时间复杂度的期望达到真正意义的O(n * logn);
将双指针版的快排做如下修改：

//修改前：
int x=array[l];  //选取第一个元素作为轴元素
//修改后
int x = nums[left + random.nextInt(right - left + 1)];

四.归并排序

归并排序和快排采用的均是分治思想；
主要思路：

1. 不断以中点为轴，划分左右区间；
2. 不断对左区间进行同样方式的划分，直到无法划分，返回
3. 不断对右区间进行同样方式的划分，直到无法划分，返回
4. 重复对有序区间[l,mid]和[mid+1,r]的元素进行合并，直到合并成完整区间

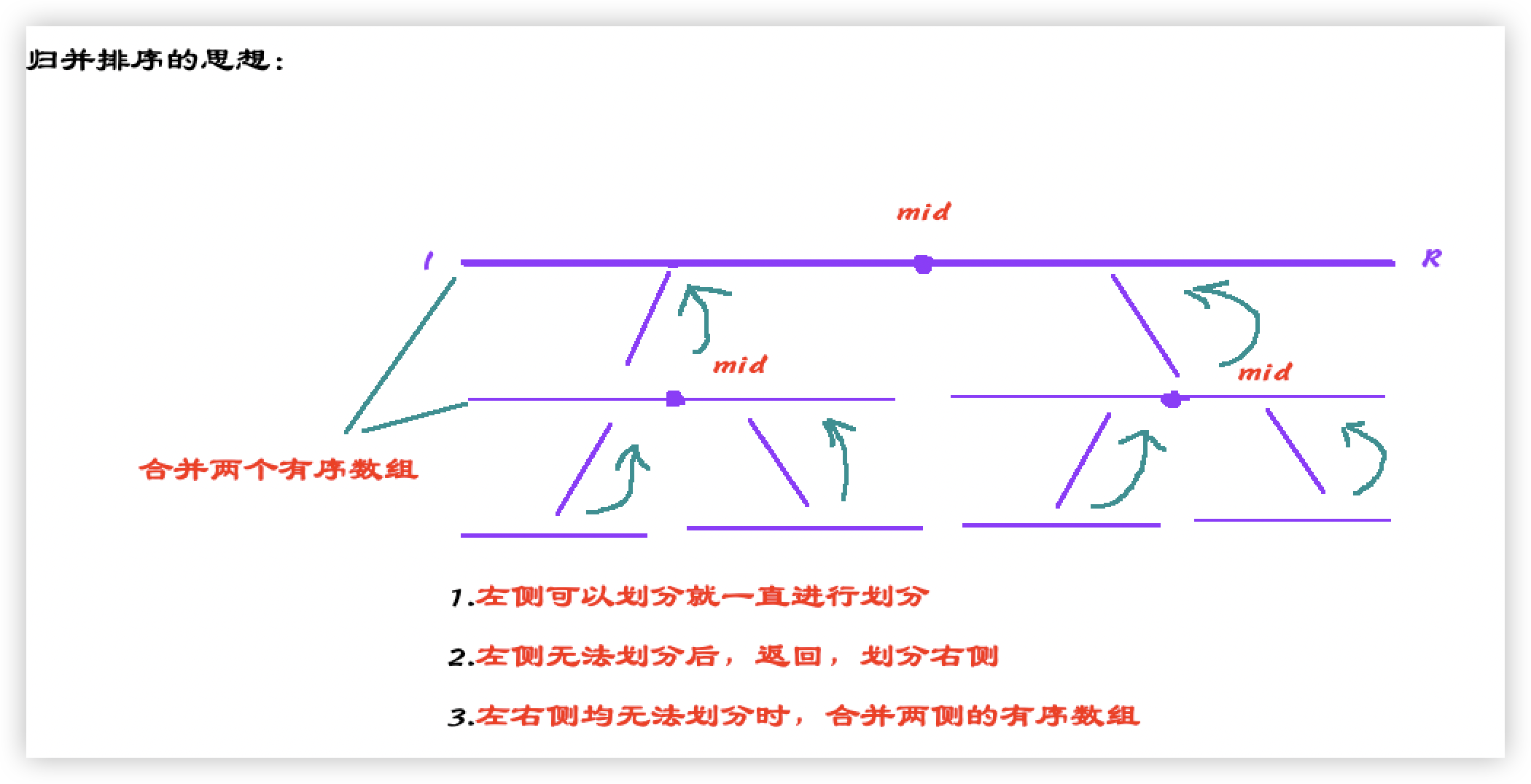
如上，可以看着归并排序本质就是树的后序遍历(左右中)；

public static int[] tmp;public static void mergeSort(int[] array,int l,int r) {//如过区间只要1个元素或者下标越界，直接返回if(l>=r) {return ;}//划分区间=》找中间点int mid=l+(r-l)/2;//划分左区间mergeSort(array, l, mid);//左区间无法划分时，划分右区间mergeSort(array, mid+1, r);//合并区间： [l,mid]+[mid+1,r] => [l,r]//tmp=new int[r-l+1]  =>可以在递归中定义，但每次递归均需要定义，因此建议写成全局变量int p1=l,p2=mid+1,p=0;while(p1<=mid&&p2<=r) {tmp[p++]=(array[p1]<array[p2])?array[p1++]:array[p2++];}while(p2<=r) {tmp[p++]=array[p2++];}while(p1<=mid) {tmp[p++]=array[p1++];}//将合并后的数组还原到原数组for(int i=l;i<=r;i++) {array[i]=tmp[i-l];}
}public static void sortArray(int[] nums) {tmp=new int[nums.length];mergeSort(nums, 0, nums.length-1);
}

归并排序的特点：

• 归并排序的时间复杂度为O(nlog(n)),空间复杂度为O(n)
• 归并排序是稳定的算法
• 归并排序的缺点是O(n)的空间复杂度，更多用在外排序中

五.总结

排序方式	最好时间复杂度	最坏时间复杂度	空间复杂度	稳定性
冒泡排序	O(n^2)	O(n^2)	O(1)	稳定
插入排序	O(n)	O(n^2)	O(1)	稳定
选择排序	O(n^2)	O(n^2)	O(1)	不稳定
希尔排序	O(n)	O(n^2)	O(1)	不稳定
堆排序	O(n* logn)	O(n* logn)	O(1)	不稳定
快速排序	O(n* logn)	O(n^2)	O(logn)~O(n)	不稳定
归并排序	O(n* logn)	O(n* logn)	O(n)	稳定