P8456 「SWTR-8」地地铁铁 题解

Description

原题意很简洁。

主要注意简单路径不能经过重复的节点。

Solution

小清新图论题，给出题人点赞。

不能重复经过节点，那实际上一条路径就是走进一个点双、过割点、然后再进一个点双。

于是很自然地建一棵广义圆方树。

情况分为两种，$(x,y)$ 在同一点双和在不同点双。

先考虑在同一点双，按照点双里面有的边的种类再分为只有一种和两种都有。

对于第一种，那没办法，这个点双肯定没有合法的点对，总不能走出去再进来吧。

对于第二种，由于点双的性质，任一对点对间至少有两条点不交的路径，只有两点之间每一条路径都只有一种字母才不合法（而且一个点双中最多只有一对），否则一定合法，形如这样：

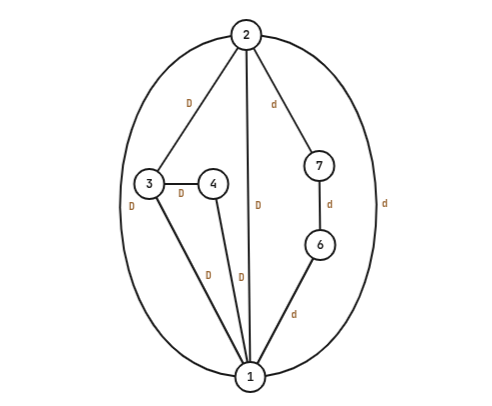
图中 $(1,2)$ 就是一对不合法的点对，而其他所有点对 $(x,y)$ 都合法。

若 $x,y$ 都在同一种边上，如 $(6,7)$，就有 $7\to \cdots \to 2\to \cdots \to 1\to \cdots \to 6$ 这种路径，$2\to \cdots \to 1$ 走与 $7\to \cdots \to 2$ 不同的边即可，否则如 $(3,6)$ 这种，就有 $3\to \cdots \to 1/2\to \cdots \to 6$ 这样子的路径。

如果不存在 $(1,2)$ 这种点对，那 $(x,y)$ 间若干条路径一定有一条是 d和 D都有的，不然就是 $(1,2)$ 了。

如何判断一个点双中是否有这种点对呢？

发现只有 $1$ 和 $2$ 与两种边都相连，因为如果有第三个点 $x$ 也是这样的，那么一定存在合法路径 $1\to x\to 2$。

所以只要计算点双中与两种边都相连的点的数量，如果其为 $2$，那么这个点双的贡献为 $\frac{size\times (size-1)}{2}-1$，否则为 $\frac{size\times (size-1)}{2}$。

然后考虑 $(x,y)$ 不在同一点双的情况。

首先对每个方点求出其 $pos$ 值，$pos=1$ 表示此点双只有 d边，$pos=2$ 表示只有 D边，$pos=3$ 表示两种边都有。

找到 $(x,y)$ 在圆方树上路径中所有方点，只要出现了 $pos=3$ 的或者 $pos=1/2$ 都出现了，就是合法的。

但是会发现一个问题，如果 $pos=3$ 的方点在路径上的与它相连的两个圆点恰好就分别是上图中 $1$ 和 $2$ 那样，那这个点双就只能提供一种边。

由于现在求的是跨过这个点双的路径，所以还要走其他的点双，不管其他提供的哪种边，这个点双给另外一种边就合法了。

至于怎么求，圆方树上树形 dp即可。这种 dp多写就好了，推荐 P10140。

$f_{x,1/2/3}$ 表示 $x$ 这个点的子树内有多少个圆点到 $x$ 的路径上已经是 $1/2/3$ 类型（定义与 $pos$ 类似）了，注意圆点和方点的区别，圆点的 $f$ 是不含自己的，方点则是不含上面那个圆点的，以及在方点算贡献更复杂，具体实现见代码。

时间复杂度是 $O(n+m)$，复杂度瓶颈在于怎么求每个点双中与两种边都相连的点的数量。

如果遍历点双的导出子图，然后判断每个点的话，在菊花图中会被卡成 $O(n^2)$。

所以直接对每条边考虑，若两端点在同一点双 $b$ 内就把这条边放到 $a_b$ 中，计算 $b$ 的 $pos$ 与贡献时遍历 $a_b$ 即可。至于找 $b$，圆方树上两点中间的方点就是 $b$，复杂度 $O(n+m)$。

Code

#include<bits/stdc++.h>
using namespace std;
#define pb push_back
#define ll long long
const int N=4e5+10,M=1e6+10;
int c,n,m,tot,cnt,fl;
int head[N],dfn[N],low[N],pos[N],fa[2*N],f[2*N][4];
bool vis[N][3],ff[3];
ll ans;
stack<int> s;
vector<int> v[2*N];
vector<pair<int,int> > a[N];
struct edge{int to,next,tp;
}e[2*M];
void add(int x,int y,char z){e[++tot]={y,head[x],z=='d'?1:2};head[x]=tot;
}
int find(int x,int y){  //找点双if(fa[x]==fa[y]) return fa[x];if(x==fa[fa[y]]) return fa[y];if(y==fa[fa[x]]) return fa[x];return 0;
}
void dfs(int x,int fax){s.push(x);dfn[x]=low[x]=++cnt;for(int i=head[x];i;i=e[i].next){int y=e[i].to;if(y==fax) continue;if(dfn[y]) low[x]=min(low[x],dfn[y]);else{dfs(y,x);low[x]=min(low[x],low[y]);if(low[y]>=dfn[x]){fl++;while(s.top()!=y){v[fl].pb(s.top());v[s.top()].pb(fl);s.pop();}s.pop();v[fl].pb(y),v[y].pb(fl);v[fl].pb(x),v[x].pb(fl);}}}
}
void get(int x,int fax){fa[x]=fax;for(int y:v[x]){if(y==fax) continue;get(y,x);}
}
void sol(int x,int fax){int sav[4]={0,0,0,0};for(int y:v[x]){if(y==fax) continue;sol(y,x);if(x<=n){ans+=(ll)f[y][1]*(sav[2]+sav[3]);  //圆点处算贡献不用考虑啥ans+=(ll)f[y][2]*(sav[1]+sav[3]);ans+=(ll)f[y][3]*(sav[1]+sav[2]+sav[3]);}else{  //方点处要考虑路径的终点是在点双内还是在另一棵子树内if(pos[x-n]==1) ans+=(ll)(v[x].size()-1)*(f[y][2]+f[y][3]);  //终点在该点双内else if(pos[x-n]==2) ans+=(ll)(v[x].size()-1)*(f[y][1]+f[y][3]);else ans+=(ll)(v[x].size()-1)*(f[y][1]+f[y][2]+f[y][3]);  //v[x].size()-1的原因是不算这棵子树与方点直接相连的那个圆点，因为在下面已经算过了ans+=(ll)f[y][1]*(sav[2]+sav[3]);  //只是经过点双ans+=(ll)f[y][2]*(sav[1]+sav[3]);ans+=(ll)f[y][3]*(sav[1]+sav[2]+sav[3]);if(pos[x-n]==1||pos[x-n]==3) ans+=(ll)f[y][2]*(sav[2]);if(pos[x-n]==2||pos[x-n]==3) ans+=(ll)f[y][1]*(sav[1]);}for(int i=1;i<=3;i++)sav[i]+=f[y][i];}if(x<=n){for(int i=1;i<=3;i++) f[x][i]=sav[i];}else if(pos[x-n]==1){f[x][1]=v[x].size()-1+sav[1];f[x][3]=sav[2]+sav[3];}else if(pos[x-n]==2){f[x][2]=v[x].size()-1+sav[2];f[x][3]=sav[1]+sav[3];}else f[x][3]=v[x].size()-1+sav[1]+sav[2]+sav[3];
}
int main(){ios::sync_with_stdio(0);cin.tie(nullptr);cin>>c>>n>>m;for(int i=1;i<=m;i++){int x,y;char z;cin>>x>>y>>z;add(x,y,z);add(y,x,z);}fl=n;dfs(1,0);get(1,0);for(int x=1;x<=n;x++){  //将每条边预处理进一个点双for(int i=head[x];i;i=e[i].next){int y=e[i].to,z=find(x,y);if(!z) continue;a[z-n].push_back({x,e[i].tp});}}for(int i=n+1;i<=fl;i++){  //求与两种边都相连的点的数量int tmp=0;ff[1]=ff[2]=0;for(int x:v[i]) vis[x][1]=vis[x][2]=0;for(auto [x,tp]:a[i-n]) vis[x][tp]=ff[tp]=1;for(int x:v[i]) tmp+=(vis[x][1]&vis[x][2]);pos[i-n]=ff[1]+ff[2]*2;if(pos[i-n]==3) ans+=(ll)v[i].size()*(v[i].size()-1)/2-(tmp==2);}sol(1,0);cout<<ans<<'\n';return 0;
}