当前位置：首页 > news >正文

【3DV 进阶-3】Hunyuan3D2.1 训练代码详细理解之-Flow matching 训练 loss 详解

news 2025/9/12 11:53:38

【3D 入门-指标篇上】3D 网格重建评估指标详解与通俗比喻
【3D 入门-指标篇下】 3D重建评估指标对比-附实现代码
【3D 入门-3】常见 3D 格式对比，.glb / .obj / .stl / .ply
【3D 入门-4】trimesh 极速上手之 3D Mesh 数据结构解析（Vertices / Faces）
【3D 入门-5】trimesh 极速上手之 Hunyuan3D-2.1 中的“非水密网格“处理流程
【3D 入门-6】大白话解释 SDF(Signed Distance Field) 和 Marching Cube 算法
【3D 入门-7】理解 SDF(Signed Distance Field) 不是什么？与相对坐标的区别
【3D 入门-8】通过 Hunyuan3D2.1 的代码来理解 SDF 和 marching cubes（上）
【3D 入门-9】通过 Hunyuan3D2.1 的代码来理解 SDF 和 marching cubes（下）
【3DV 进阶-1】Hunyuan3D2.1 训练代码详细理解上-模型调用流程
【3DV 进阶-2】Hunyuan3D2.1 训练代码详细理解下-数据读取流程
Rectified Flow 相关：【整流模型（一） / 扩散模型（十一）】SD1.5 / SDXL / SD3 / Flux 整体区别梳理汇总，扩散与整流（Rectified Flow）的区别

Loss 计算的关键代码位于 /pathHunyuan3D-2.1/hy3dshape/hy3dshape/models/diffusion/transport/transport.py

总结下训练目标，和图像生成类似：

可以“宽松地”理解为：denoiser 在潜变量空间学习“如何从噪声生成 latent（latent 由 surface 通过 ShapeVAE 编码而来）”，从而在采样时重建/生成这个 latent。
严格来说，它不是直接对 latent 做回归重建，而是用 Flow matching 的训练目标，学习噪声→数据路径上的“速度/噪声”（vector field/score）。
- 监督信号由 VAE 编码得到的 z 和随机时间 t 决定的目标速度/噪声给出。

具体的代码理解如下：

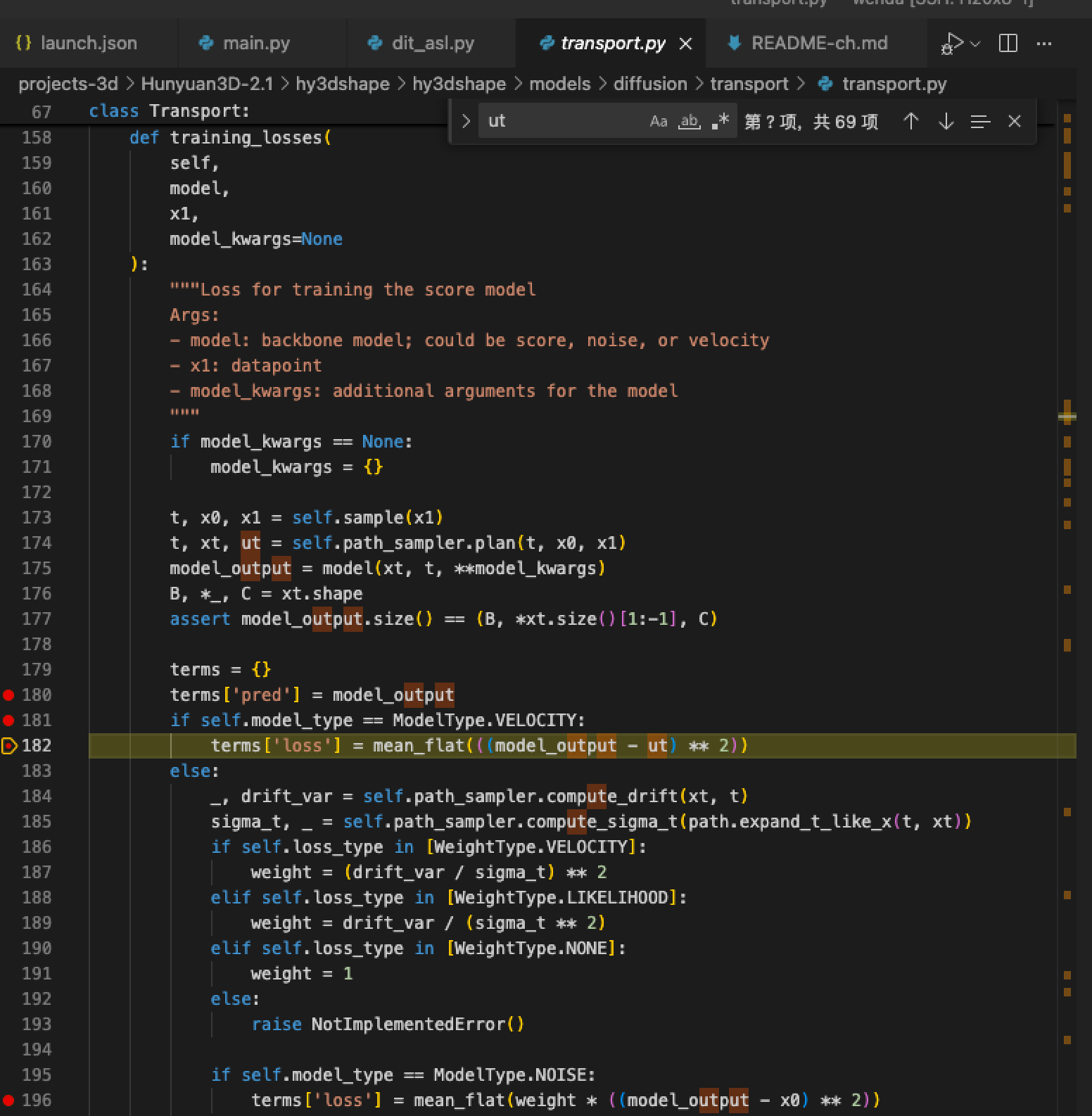
training_losses

输入是 x1（lantent）
关键步骤是 self.sample(x1) 和 self.path_sampler.plan
最后通过对 **model_output 和 ut （GT）**之前的 MSE loss (均方误差)

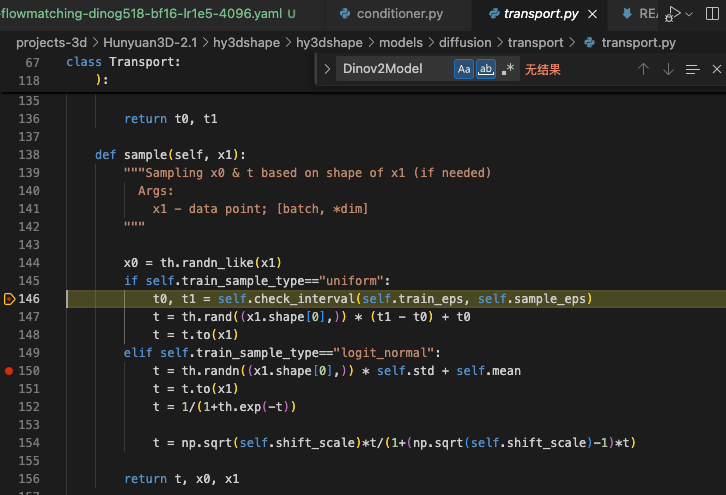
sample(x1)

x1（数据点）: 目标分布的样本，形状与模型输出一致。在本项目里就是 VAE 对 surface 编码得到的潜变量 latents（即要“生成/重建”的对象）。
x0（噪声起点）: 与 x1 同形状的标准正态随机张量 th.randn_like(x1)，代表从高斯先验出发的“源分布”。
t（时间标量）: 每个样本一个标量，表示在“从 x0 走到 x1”的路径上的位置。
采样方式：
- uniform: 在 (t0, t1) 上均匀采样，区间由 check_interval(self.train_eps, self.sample_eps) 决定，以避开端点的数值不稳定。
- logit_normal: 先按高斯采样再经 sigmo id、shift_scale 映射，得到偏向某些时间段的分布。
  形状为 [batch]，每个样本一个 t。
- 返回的是 (t, x0, x1)；随后用路径规划器得到中间状态和监督目标（速度/向量场）

self.path_sampler.plan(t, x0, x1)

x1（数据样本）: 真实分布的样本。在本项目中是 VAE 对 surface 编码得到的 latent，作为“目标端”。
x0（噪声起点）: 与 x1 同形状的标准高斯噪声，作为“源端”，从这里出发要被运输到 x1。
t（时间标量）: 每个样本一个 t∈(0,1)，表示在“从 x0 到 x1”的路径上的位置。训练时随机采样覆盖全时刻。
xt（路径上的点）: 在给定 t 下，路径定义（Linear/VP/GVP）算出的中间状态，模型的输入之一。
ut（目标速度/向量场）: 在给定路径与 t 下的“真速度”/“所需运输方向”。例如 Linear 时 ut = x1 - x0（与 t 无关）。
model_output: 模型对给定 (xt, t, cond) 预测的速度（或等价的噪声/score 的重参数化）。

path_sampler.plan 代码具体做了什么？

路径类型: 由配置的 path_type 决定，映射见 Transport 内部（Linear→ICPlan，VP→VPCPlan，GVP→GVPCPlan）。核心接口一致：返回 (t, xt, ut)。
以 Linear 路径 ICPlan 为例（最直观）：
- 将标量 t 广播到 x 的形状维度以便逐元素计算：

def expand_t_like_x(t, x):dims = [1] * (len(x.size()) - 1)t = t.view(t.size(0), *dims)return t

系数与导数：
- alpha_t = t（乘在数据端 x1 上），sigma_t = 1 - t（乘在噪声端 x0 上）
- d_alpha_t = 1，d_sigma_t = -1

def compute_alpha_t(self, t): return t, 1
def compute_sigma_t(self, t): return 1 - t, -1

路径上的点 x_t 与目标速度/向量场 u_t：
- x_t = alpha_t * x1 + sigma_t * x0 = t * x1 + (1 - t) * x0
- u_t = d_alpha_t * x1 + d_sigma_t * x0 = x1 - x0（线性情形下与 t 无关）

def compute_mu_t(self, t, x0, x1):t = expand_t_like_x(t, x1)alpha_t, _ = self.compute_alpha_t(t)sigma_t, _ = self.compute_sigma_t(t)return alpha_t * x1 + sigma_t * x0def compute_xt(self, t, x0, x1):xt = self.compute_mu_t(t, x0, x1); return xtdef compute_ut(self, t, x0, x1, xt):t = expand_t_like_x(t, x1)_, d_alpha_t = self.compute_alpha_t(t)_, d_sigma_t = self.compute_sigma_t(t)return d_alpha_t * x1 + d_sigma_t * x0def plan(self, t, x0, x1):xt = self.compute_xt(t, x0, x1)ut = self.compute_ut(t, x0, x1, xt)return t, xt, ut

在训练里如何用:
- 用 plan 得到 (t, x_t, u_t)，把 x_t, t 喂给模型，预测 model_output，用 MSE 对齐目标 u_t：

t, x0, x1 = self.sample(x1)
t, xt, ut = self.path_sampler.plan(t, x0, x1)
model_output = model(xt, t, **model_kwargs)
terms['loss'] = mean_flat(((model_output - ut) ** 2))