当前位置：首页 > news >正文

手眼标定之已知同名点对，求解转换RT，备份记录

news 2025/9/12 9:19:40

机器人手眼标定，往往需要获取相机和机器人末端工具和相机坐标系的转换关系，此处只介绍一种眼在手外，3D相机的解算方法

前提条件

获取到机器人工具坐标系下和3D相机坐标系下的同名点
方法：
1.可以自动获取，通过放固定模型的靶标，识别靶标中心点一类的，如小圆柱体顶面圆心
2.手动拾取，关联2D和3D相机像素和深度，直接在图像上拾取平面位置和深度

求解转换关系

公式可以完成参考这篇文章，人家写的很好，而且另一篇有严密推导，似懂非懂，我直接借用公式了

转载：https://blog.csdn.net/u012836279/article/details/80203170

这篇文章是拿python写的，我不会用，我用C++复现和测试一下
基本原理和公式贴一下图
去中心化，如果两组点是同名点，去中心化后应该只有旋转变换了，先求旋转在算偏移
1.计算重心，即XYZ求均值即可
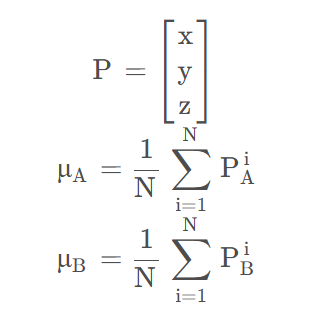
在这里插入图片描述
2.去中心化，即每个点减去重心

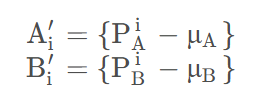
3.构建协方差矩阵

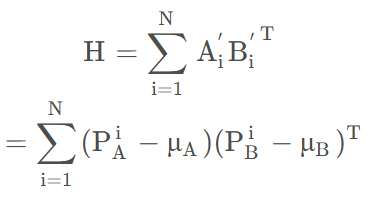
4.SVD分解，SVD分解后R = VUT

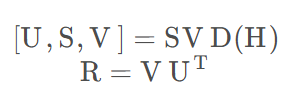
5. 求平移量，用俩重心算

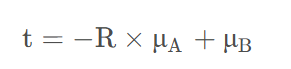
贴上C++代码验证一下

我找了三组数据，都是先找的点，在3D软件中，任意做了旋转平移刚性变换，数据抄出来使用的，算是能验证精度了，当前可以适当更改一下加点误差，看看算出来误差和坐标还准不准

#include <Eigen/Dense>
#include <Eigen/SVD>
#include <iostream>
#include <vector>Eigen::Vector3d CalculateCenxyz(Eigen::MatrixXd xyzvec)
{double xsum = 0;double ysum = 0;double zsum = 0;int num = xyzvec.rows();for (int i = 0; i < num; i++) {xsum += xyzvec(i,0);ysum += xyzvec(i,1);zsum += xyzvec(i,2);}return Eigen::Vector3d(xsum / num, ysum / num, zsum / num);
}
Eigen::MatrixXd CalculateSubCenxyz(Eigen::MatrixXd xyzvec, Eigen::Vector3d cenxyz) {int num = xyzvec.rows();Eigen::MatrixXd out;out.resize(num, 3);for (int i = 0; i < num; i++) {out(i, 0) = xyzvec(i, 0) - cenxyz[0];out(i, 1) = xyzvec(i, 1) - cenxyz[1];out(i, 2) = xyzvec(i, 2) - cenxyz[2];}return out;
}
float CalculateRT(std::vector<Eigen::Vector3d>src, std::vector<Eigen::Vector3d>dst, Eigen::Matrix4d &RT) {//参数计算的格式Eigen::MatrixXd A, B;A.resize(src.size(), 3);B.resize(dst.size(), 3);for (int i = 0; i < src.size(); i++) {A(i, 0) = src[i][0]; A(i, 1) = src[i][1]; A(i, 2) = src[i][2];}for (int i = 0; i < dst.size(); i++) {B(i, 0) = dst[i][0]; B(i, 1) = dst[i][1]; B(i, 2) = dst[i][2];}if (src.size() != dst.size()){return -1;}const int N = src.size(); // 点数const int d = 3; // 维度//计算质心点Eigen::Vector3d srccenxyz, dstcenxyz;srccenxyz = CalculateCenxyz(A);dstcenxyz = CalculateCenxyz(B);//去中心化Eigen::MatrixXd srccentered = CalculateSubCenxyz(A, srccenxyz);Eigen::MatrixXd dstcentered = CalculateSubCenxyz(B, dstcenxyz);//构建协方差矩阵Eigen::MatrixXd H = srccentered.transpose() * dstcentered;//对H进行SVD分解Eigen::JacobiSVD<Eigen::MatrixXd> svd(H, Eigen::ComputeFullU | Eigen::ComputeFullV);//计算旋转矩阵R (使用SVD结果)Eigen::MatrixXd R = svd.matrixV() * svd.matrixU().transpose();// 确保旋转矩阵的行列式为+1 (避免反射)if (R.determinant() < 0) {Eigen::MatrixXd V = svd.matrixV();V.col(3 - 1) *= -1; // 将最后一列取反R = V * svd.matrixU().transpose();}//计算平移矩阵Eigen::Vector3d t = dstcenxyz - R * srccenxyz;// 8. 计算变换后的点集Eigen::MatrixXd A_transformed = (A * R.transpose()).rowwise() + t.transpose();std::cout << "变换后的点集A:\n" << A_transformed << "\n\n";std::cout << "原始点集B:\n" << B << "\n\n";// 9. 计算变换误差Eigen::MatrixXd error = B - A_transformed;double rmse = sqrt(error.array().square().sum() / (N * d));RT(0, 0) = R(0, 0); RT(0, 1) = R(0, 1); RT(0, 2) = R(0, 2); RT(0, 3) = t[0];RT(1, 0) = R(1, 0); RT(1, 1) = R(1, 1); RT(1, 2) = R(1, 2); RT(1, 3) = t[1];RT(2, 0) = R(2, 0); RT(2, 1) = R(2, 1); RT(2, 2) = R(2, 2); RT(2, 3) = t[2];RT(3, 0) = 0; RT(3, 1) = 0; RT(3, 2) = 0; RT(3, 3) = 1;return rmse;
}
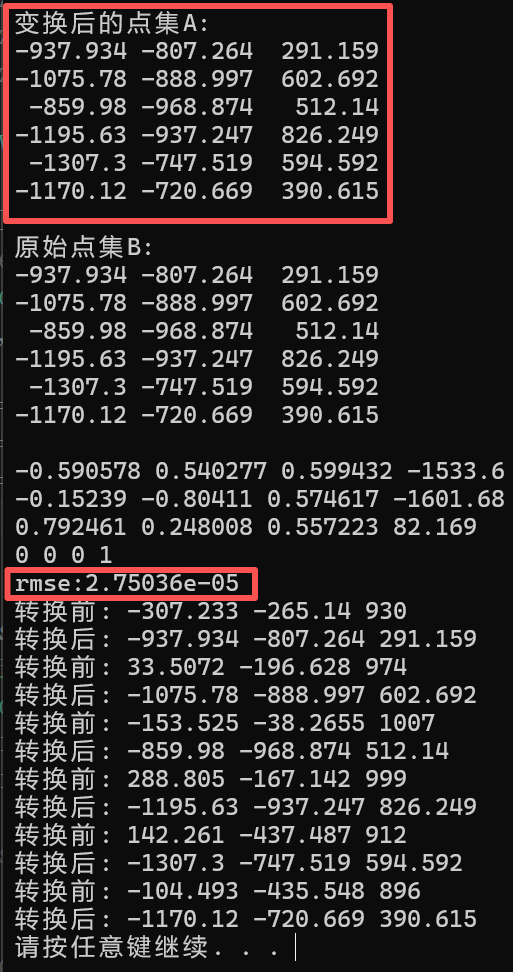
int main() {//外部做接口做成这个Eigen::Vector3d格式std::vector<Eigen::Vector3d>src,dst;src.push_back(Eigen::Vector3d(-307.233, -265.14, 930));src.push_back(Eigen::Vector3d(33.5072, -196.628, 974));src.push_back(Eigen::Vector3d(-153.525, -38.2655, 1007));src.push_back(Eigen::Vector3d(288.805, -167.142, 999));src.push_back(Eigen::Vector3d(142.261, -437.487, 912));src.push_back(Eigen::Vector3d(-104.493, -435.548, 896));dst.push_back(Eigen::Vector3d(-937.93444824 , -807.26367188, 291.15930176));dst.push_back(Eigen::Vector3d(-1075.77783203, -888.99725342, 602.69195557));dst.push_back(Eigen::Vector3d(-859.97985840 , -968.87390137, 512.13989258));dst.push_back(Eigen::Vector3d(-1195.63476563, -937.24676514, 826.24877930));dst.push_back(Eigen::Vector3d(-1307.30078125, -747.51934814, 594.59216309));dst.push_back(Eigen::Vector3d(-1170.11645508, -720.66943359, 390.61462402));/*src.push_back(Eigen::Vector3d(100, 0, 0));src.push_back(Eigen::Vector3d(100, 100, 100));src.push_back(Eigen::Vector3d(0, 100, 0));src.push_back(Eigen::Vector3d(0, 0, 100));dst.push_back(Eigen::Vector3d(-108.54067993, -37.01885223, -190.20104980));dst.push_back(Eigen::Vector3d(-2.08551025, -94.98533630, -117.35063171));dst.push_back(Eigen::Vector3d(-135.92652893, -121.73773193, -80.32509613));dst.push_back(Eigen::Vector3d(-83.49967957, -175.86019897, -200.00042725));*///src.push_back(Eigen::Vector3d(100, 0, 1));//src.push_back(Eigen::Vector3d(500, 0, 5));//src.push_back(Eigen::Vector3d(0, 100, 3));//src.push_back(Eigen::Vector3d(0, 500, 4));//dst.push_back(Eigen::Vector3d(6040.03369141, 2504.92944336, -64.71488953));//dst.push_back(Eigen::Vector3d(6108.16162109, 2302.78710938, 273.68286133));//dst.push_back(Eigen::Vector3d(5981.70751953, 2629.77734375, -96.57476807));//dst.push_back(Eigen::Vector3d(5826.48486328, 2931.66308594, 115.01904297));Eigen::Matrix4d RT;float rmse = CalculateRT(src, dst, RT);std::cout << RT(0, 0) << " " << RT(0, 1) << " " << RT(0, 2) << " " << RT(0, 3) << std::endl;std::cout << RT(1, 0) << " " << RT(1, 1) << " " << RT(1, 2) << " " << RT(1, 3) << std::endl;std::cout << RT(2, 0) << " " << RT(2, 1) << " " << RT(2, 2) << " " << RT(2, 3) << std::endl;std::cout << RT(3, 0) << " " << RT(3, 1) << " " << RT(3, 2) << " " << RT(3, 3) << std::endl;std::cout << "rmse:" << rmse<<std::endl;for (int i = 0; i < src.size(); i++) {Eigen::Vector4d srcp(src[i][0], src[i][1], src[i][2], 1.0);Eigen::Vector4d dstp = RT * srcp;std::cout << "转换前: " << srcp[0] << " " << srcp[1] << " " << srcp[2] << std::endl;std::cout << "转换后: " << dstp[0] << " " << dstp[1] << " " << dstp[2] << std::endl;}return 0;
}