当前位置：首页 > news >正文

掌握梯度提升：构建强大的机器学习模型介绍

news 2025/9/12 9:16:18

本篇文章Master Gradient Boosting for Powerful Machine Learning Models适合希望深入了解梯度提升（GBM）技术的读者。文章的亮点在于清晰地解释了GBM的工作原理，并比较了不同GBM模型（如XGBoost、LightGBM和CatBoost）的特点与性能。

文章目录

1 引言
2 什么是梯度提升
3 什么是集成学习技术
- 3.1 Bagging
- 3.2 Boosting
- 3.3 Snapshot Ensemble
- 3.4 权重平均
- 3.5 Stacking
- 3.6 投票法
4 GBM 的工作原理
- 4.1 弱学习器的输出
- 4.2 优化步长
- - 4.2.1 XGBoost (Extreme Gradient Boosting)
  - 4.2.2 LightGBM (Light Gradient-Boosting Machine)
  - 4.2.3 CatBoost (Categorical Boosting)
5 模拟实验
- 5.1 定义自定义分类器
- 5.2 数据集准备
- 5.3 模型调优
- 5.4 评估
- 5.5 结果
6 结论

1 引言

集成学习技术是机器学习中常见的技术，用于提高模型预测的准确性。

在本文中，我将从理论和编码模拟两个方面，深入探讨梯度提升（Gradient Boosting），这是一种广泛使用的集成策略。

2 什么是梯度提升

梯度提升（或梯度提升机，GBM）是一种集成学习技术，属于**提升（boosting）**范畴，它通过顺序构建弱模型来捕捉复杂的非线性依赖关系。

在此过程中，每个弱模型（通常是只有几个叶节点的浅层决策树）都试图使用梯度下降算法来最小化前一个模型的损失（残差），并整体上改进预测。

3 什么是集成学习技术

在详细介绍 GBM 之前，让我们快速了解一下机器学习中集成学习技术的概况。

其基本概念是结合多个模型（或深度学习中的神经元）以提高整体预测准确性和鲁棒性。提升是其中一种技术，但我们还有许多其他选择。

以下是集成学习技术的核心框架：

3.1 Bagging

在自助采样（bootstrap samples）上独立训练多个模型，然后对其预测进行平均/投票。
目标：降低方差。
主要例子：随机森林（Random Forest）（一种经典的 Bagging 方法，由决策树集成）。

3.2 Boosting

顺序训练模型，每个模型都纠正前一个模型的错误。
目标：降低偏差。
主要例子：梯度提升（Gradient Boosting）、AdaBoost（自适应提升，为错误分类的训练样本分配权重）。

3.3 Snapshot Ensemble

在深度学习中，训练单个神经网络并对其预测进行平均，以避免训练多个大型网络。

3.4 权重平均

训练多个模型并平均它们的权重（在深度学习中）。
主要方法包括随机权重平均（Stochastic Weight Averaging, SWA）。

3.5 Stacking

通过在基础模型的输出上训练一个元模型（或“元学习器”），来结合多个不同的基础模型的预测。

3.6 投票法

一种决定模型预测胜者的方法。
硬投票（多数投票）：获得单个模型最多票数的类别获胜。
软投票（加权平均）：对于分类任务，平均概率最高的类别获胜。对于回归任务，通常是平均预测值。

4 GBM 的工作原理

GBM 通过在简单的基础模型（所谓的“弱学习器”）上不断构建一个经过优化的集成模型，以最小化人类通过损失函数定义的损失。

下图展示了集成模型 $F$ 如何通过添加弱学习器（ $h$ ，红色、黄色和绿色表示）来不断优化预测的整个过程。

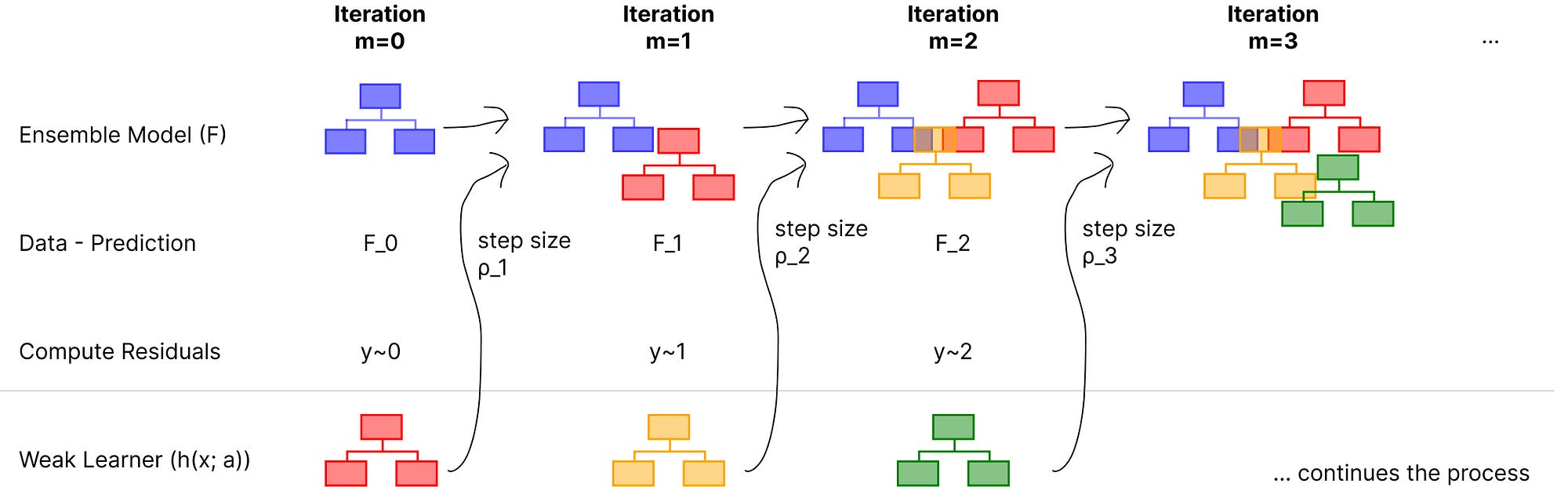
图：梯度提升利用简单决策树作为学习器的迭代过程

以随机迭代 $m$ 为例，此过程定义为将新弱学习器的输出添加到前一次迭代中集成模型的输出：

$F_m(x)$ ：第 $m$ 次迭代后更新的集成模型。
$F_{m-1}(x)$ ：前一次（第 $m - 1$ 次）迭代的集成模型。
$ρm\rho_m$ ：定义新弱学习器步长的缩放因子。
$h(x; a_m)$ ：在当前（第 $m$ 次）迭代中添加到集成模型中的弱学习器。

步长和新弱学习器的输出都影响最终预测。因此，我们将分别探讨它们。

4.1 弱学习器的输出

弱学习器被训练来预测伪残差（或残差， $y~i\tilde{y}_i$ ，也称为负梯度）。

残差表示集成模型损失函数最陡峭下降的方向和幅度，针对每个训练样本。

在数学上，这些值是通过对损失函数（ $L$ ）相对于集成模型的预测（ $F(x_i)$ ）求负偏导（梯度）来计算的：

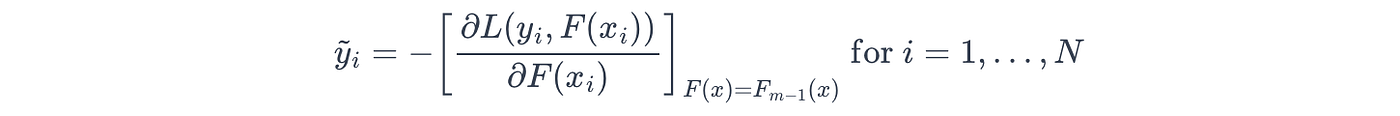
然后，算法通过调整其模型参数（ $a_m$ ），引导新的弱学习器（ $h(x; a_m)$ ）纠正这些错误，使其朝着损失最小化的方向发展：

在公式中，缩放因子（ $β\beta$ ）表示学习率或分配给弱学习器的权重。在某些实现中， $β\beta$ 可能会单独优化或固定。

4.2 优化步长

训练完弱学习器后，算法决定最佳步长（ $ρ\rho$ ），它定义了新弱学习器对集成模型贡献的程度。

在数学上，最佳步长是通过线搜索找到的，其中集成模型最小化_更新_预测与其相应真实标签之间的损失（ $L$ ）：

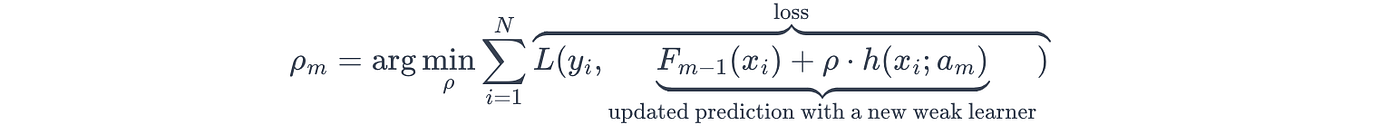
（ $y$ ：对应的真实标签， $a_m$ ：弱学习器的参数）

这是集成模型防止自身向某个弱学习器迈出过大步长，并因此过度拟合特定学习器的重要一步。

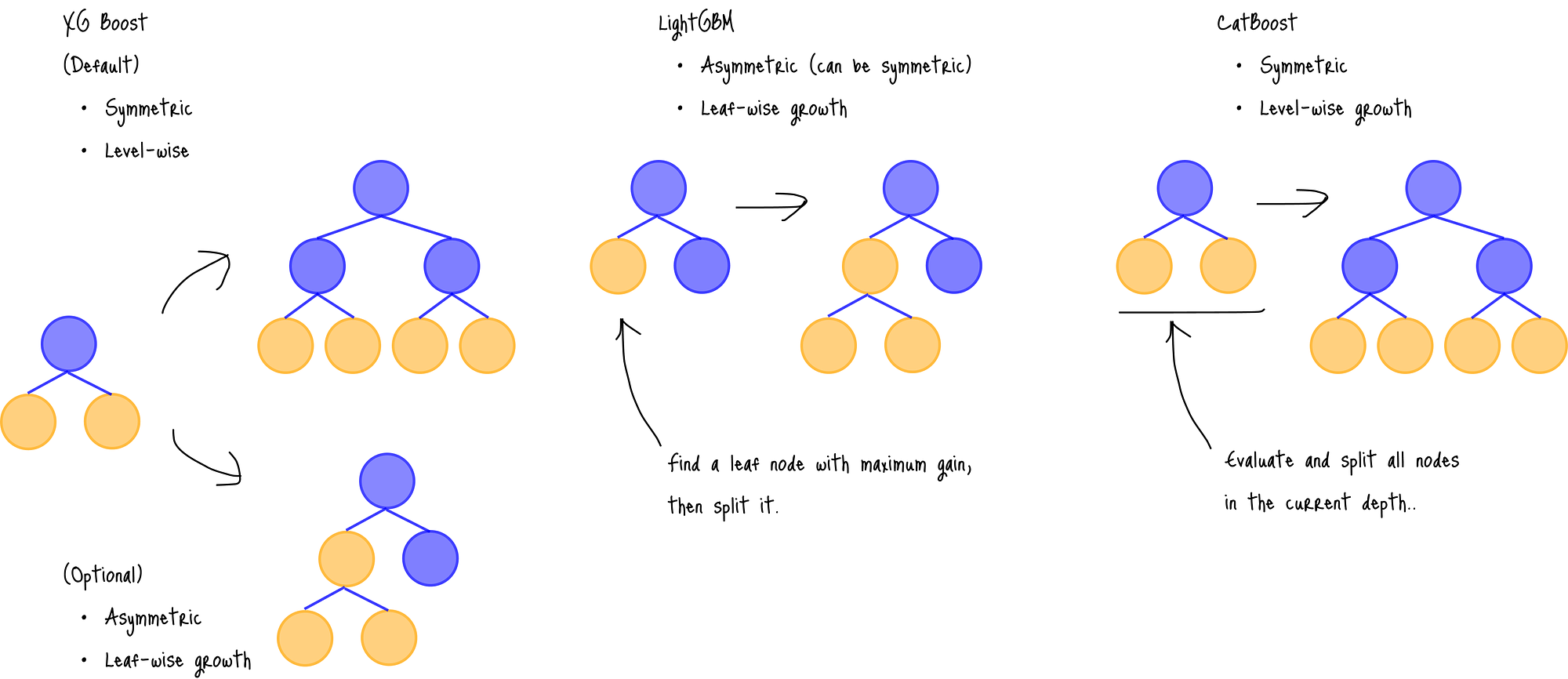
GBM 系列主要模型对比：XGBoost、LightGBM 和 CatBoost

以下是每个模型的详细比较。

4.2.1 XGBoost (Extreme Gradient Boosting)

XGBoost 是 GBM 系列中最经典的模型。

树类型：对称/非对称，**层级（level-wise）**或深度优先生长。
利用近似贪婪算法或基于直方图的算法来寻找树的最佳分裂点。
可以处理数值和类别特征（但不能处理原始文本特征）。
必须对类别特征应用编码，例如独热编码、标签编码或均值编码。
由 DMLC 开发。

4.2.2 LightGBM (Light Gradient-Boosting Machine)

LightGBM 在处理大型数据集方面表现出色，主要归功于其高效的基于直方图的算法和采样方法，如 GOSS 和 EFB。

擅长处理大型数据集。
树类型：非对称，**叶级（leaf-wise）**生长。
利用基于直方图的算法来寻找树的最佳分裂点。
基于梯度的单侧采样（Gradient-based One-Side Sampling, GOSS）：模型选择性地在训练数据的_子集_上进行训练，重点关注具有较大梯度的样本——这意味着被错误分类或拟合较差的样本。
独占特征捆绑（Exclusive Feature Bundling, EFB）：模型将很少同时取非零值的互斥特征合并到一个捆绑中，并减少特征数量以加速训练。
可以处理数值和类别特征（但不能处理原始文本特征）。
无需对类别特征应用编码。
由微软开发。

4.2.3 CatBoost (Categorical Boosting)

CatBoost 可以处理更多多样化的特征，利用其独特的Ordered Target Encoding、Ordered Boosting等方法，其效率主要来自其对称的树结构。

树类型：对称，**层级（level-wise）**生长。
可以_直接_处理数值、类别、原始文本和嵌入特征，无需显式编码。
利用**有序目标编码（Ordered Target Encoding）方案，将类别特征转换为数值；以及一种称为有序提升（Ordered Boosting）**的训练方案，在训练开始前对整个训练数据集进行随机排列，并让弱学习器只使用较早出现的数据点。
由于有序提升技术及其对称的树结构，可以内在减少过拟合。
由 Yandex 开发。

我将在下一节比较它们的性能。

5 模拟实验

我将使用 Scikit-learn、Keras 和 CatBoost 库构建以下四种模型，并比较它们的性能。

自定义 GB 分类器（CustomGB 类）
XGBoost 分类器
LightGBM 分类器
CatBoost 分类器
逻辑回归（作为主要基线模型）
深度前馈网络（作为次要基线模型）。

5.1 定义自定义分类器

我将首先定义带有 fit()、predict_proba() 和 predict() 函数的自定义分类器。

在迭代循环中，我将二元交叉熵损失定义为损失函数，并简化了残差（rho）的计算。

import numpy as np
from sklearn.tree import DecisionTreeRegressorclass CustomGB:def __init__(self, learning_rate, n_estimators, max_depth=1):self.learning_rate = learning_rateself.n_estimators = n_estimatorsself.max_depth = max_depthself.random_state = 42self.learners = []self.F_0 = Noneself.epsilon = 1e-10def fit(self, X, y):self.F_0 = np.log(y.mean() / (1 - y.mean()))F_m = np.full(len(y), self.F_0)for _ in range(self.n_estimators):p = np.exp(F_m) / (1 + np.exp(F_m))rho = y - plearner = DecisionTreeRegressor(max_depth=self.max_depth, random_state=self.random_state).fit(X, rho)terminal_node_ids = learner.apply(X)for j in np.unique(terminal_node_ids):current_id = terminal_node_ids == jgamma = rho[current_id].sum() / ((p[current_id] * (1 - p[current_id])).sum() + self.epsilon)F_m[current_id] += self.learning_rate * gammalearner.tree_.value[j, 0, 0] = gammaself.learners.append(learner)return selfdef predict_proba(self, X):F_m_pred = np.full(len(X), self.F_0)for learner in self.learners:F_m_pred += self.learning_rate * learner.predict(X)return np.exp(F_m_pred) / (1 + np.exp(F_m_pred))def predict(self, X, threshold=0.5):probabilities = self.predict_proba(X)return (probabilities >= threshold).astype(int)

5.2 数据集准备

我使用了[与投票和 stacking 方法相同的数据集]来比较性能，并在应用列转换和 SMOTE 缩放后生成了训练集、验证集和测试集：

(2826, 61) (2826,) (500, 61) (500,) (500, 61) (500,)

回顾一下，基础数据集是来自 UC Irvine 机器学习库的电信客户流失数据（根据 Creative Commons Attribution 4.0 International [(CC BY 4.0) 许可获得许可) ，包含 3,500 个数据样本和 14 个特征：

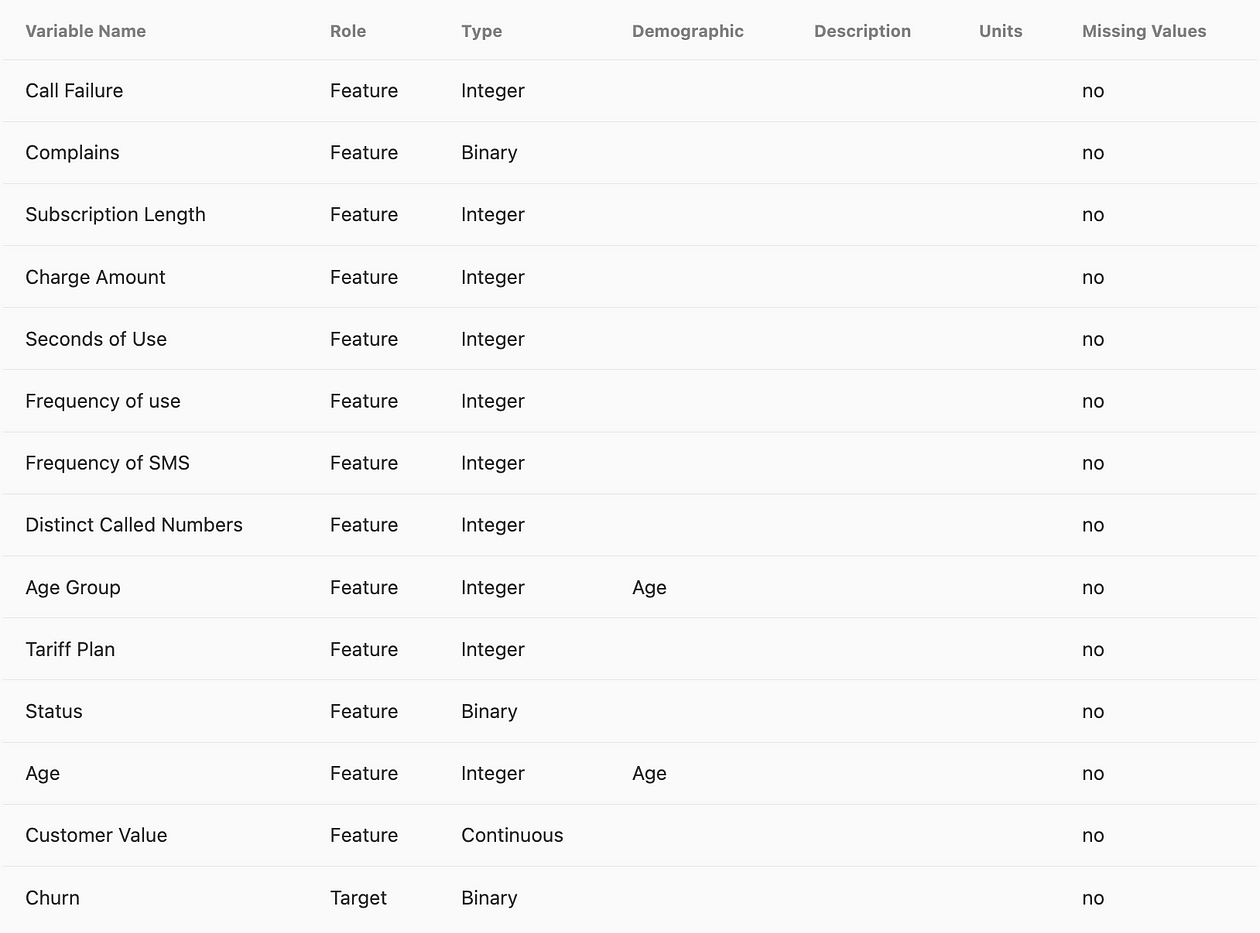
变量表

5.3 模型调优

我为所有模型设置了相似的关键参数值，以便进行公平的性能比较。

以下代码块显示了模型的基线定义，这些模型在预处理后的训练样本上进行训练。

from sklearn.ensemble import GradientBoostingClassifier, HistGradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
from catboost import CatBoostClassifierlearning_rate = 0.01
n_estimators = 5000
max_depth = 1custom_gbm = CustomGB(learning_rate=learning_rate,n_estimators=n_estimators,max_depth=max_depth
).fit(X_train_processed, y_train)sklearn_xgb = GradientBoostingClassifier(loss='log_loss',learning_rate=learning_rate,n_estimators=n_estimators,subsample=1.0,
).fit(X_train_processed, y_train)sklearn_lgb = HistGradientBoostingClassifier(loss='log_loss',learning_rate=learning_rate,max_depth=max_depth,max_iter=n_estimators,l2_regularization=0.01,early_stopping=True,validation_fraction=0.1,n_iter_no_change=10
).fit(X_train_processed, y_train)cat = CatBoostClassifier(iterations=n_estimators,learning_rate=learning_rate,depth=max_depth,loss_function='Logloss',eval_metric='Accuracy',random_seed=42,early_stopping_rounds=10
).fit(X_train_processed, y_train)sklearn_lr = LogisticRegression(penalty='l2',tol=1e-4,max_iter=n_estimators,
).fit(X_train_processed, y_train)import tensorflow as tf
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Input
keras_model = Sequential([Input(shape=(X_train_processed.shape[1],)),Dense(32, activation='relu'),Dropout(0.1),Dense(16, activation='relu'),Dropout(0.1),Dense(1, activation='sigmoid')
])
keras_model.compile(optimizer='adam',loss='binary_crossentropy',metrics=['accuracy']
)
history = keras_model.fit(X_train_processed, y_train,epochs=n_estimators,batch_size=32,validation_split=0.2,verbose=0
)

这里值得注意的是，基于外部库构建的分类器具有 L1、L2 和早停等正则化框架。

我设置了 L2 项和早停，同时确保了相对较多的 epoch 数量（n_estimators）。实际上，保持较高的 epoch 数量对于提高弱学习器的准确性至关重要。

5.4 评估

我对训练集、验证集和测试集进行了预测，并计算了准确率分数。

from sklearn.metrics import accuracy_scorey_pred_train =  model.predict(X=X_train_processed)
y_pred_val = model.predict(X_val_processed)
y_pred_test = model.predict(X=X_test_processed)
print(f'\n{model_names[i]}\nTrain: {accuracy_score(y_train, y_pred_train):.4f} Test: {accuracy_score(y_test, y_pred_test):.4f}')loss_train, accuracy_train = keras_model.evaluate(X_train_processed, y_train)
loss_val, accuracy_val = keras_model.evaluate(X_val_processed, y_val)
loss_test, accuracy_test = keras_model.evaluate(X_test_processed, y_test)
print(f"\nDFN - Train Accuracy: {accuracy_train:.4f}, Test Accuracy: {accuracy_test:.4f}")