水题记录1.7

luogu10207

link

先考虑暴力的 $n^2$ 的 $DP$

可以发现，对于多次经过一个位置的球时，只可能在最后一次拿。这样显然更优。

因此可以得出，第一个拿起的球要么是 $1$ 号球，要么是 $n$ 号球。

并且，在一定时间内所拿起的球，一定会是一段前缀和一段后缀。

考虑区间 $dp$，设 $f[l,r,0/1,0/1]$ 表示从 $1/n$ 出发，已经拿走了 $a_{1\sim l-1},a_{r+1\sim n}$ 范围内的球，当前在 $l/r$ 的方案数。

另外可以发现一个性质，去重后有效点数 $\ge 1000$ 则肯定无解，证明考虑最优情况下需要的时间也是 $n^2$ 级别的。

于是这题就做完了。

代码：

	memset(f,0x3f3f3f3f,sizeof f);f[1][n][0][0]=f[1][n][1][1]=0;for(int len=n-1;len>=1;len--){for(int l=1;l+len-1<=n;l++){int r=l+len-1;int res=cnt[a[l-1]]+cnt[m]-cnt[a[r]]+1;for(int o=0;o<=1;o++){f[l][r][o][0]=min(f[l-1][r][o][0]+res*(a[l]-a[l-1]),f[l][r+1][o][1]+res*(a[r+1]-a[l]));f[l][r][o][1]=min(f[l-1][r][o][0]+res*(a[r]-a[l-1]),f[l][r+1][o][1]+res*(a[r+1]-a[r]));}}}cin>>q;while(q--){int st,en,ti;cin>>st>>en>>ti;int ans=1e9;if(a[1]<=en){int id=upper_bound(a+1,a+n+1,en)-a-1;ans=min(ans,f[id][id][0][0]+abs(st-a[1])+(cnt[a[n]]+1)*abs(en-a[id]));ans=min(ans,f[id][id][1][0]+abs(st-a[n])+(cnt[a[n]]+1)*abs(en-a[id]));}if(en<=a[n]){int id=lower_bound(a+1,a+n+1,en)-a;ans=min(ans,f[id][id][0][0]+abs(st-a[1])+(cnt[a[n]]+1)*abs(en-a[id]));ans=min(ans,f[id][id][1][0]+abs(st-a[n])+(cnt[a[n]]+1)*abs(en-a[id]));}cout<<(ans+cnt[m]<=ti?"Yes\n":"No\n");

CF703E

link

考虑 DP，设 $f[i,j]$ 表示前 $i$ 个数选一些乘积为 $j$ 最小选的数以及所选数之和。

时间复杂度 $O(nk)$ 不可做。

考虑去掉无用状态，发现只有 $k$ 的因数状态有用，可得 $10^{12}$ 内因子最多为 $6720$

那么我们就这样子昨晚这题了，时间复杂度为 $O(nd(k)\omega (k))$

注意特判掉 $k=1$ 的情况。

需要注意的是，回溯路径的时候，需要记录当前节点用过没有，不能直接记录前驱，要不然有可能能会记录重复导致 WA。

因此可得，时间复杂度允许，用这种方式。

代码如下：

struct fy{int sum,cnt,used,pre1;
}f[N][M];for(int i=1;i<=n;i++)cin>>a[i],b[i]=__gcd(a[i],k);if(k==1){int mi=1e12,mid;for(int i=1;i<=n;i++)if(a[i]<mi)mi=a[i],mid=i;cout<<1<<"\n"<<mid<<"\n";return 0;}for(int i=1;i*i<=k;i++){if(k%i==0){d[++cd]=i;if(i*i!=k)d[++cd]=k/i;}}sort(d+1,d+cd+1);map<int,int>id;id.clear();for(int i=1;i<=cd;i++)id[d[i]]=i;int inf=0x3f3f3f3f;for(int i=0;i<N;i++)for(int j=0;j<M;j++)f[i][j]={0,inf,0,0};f[0][1]={0,0,0,0};for(int i=0;i<n;i++){for(int j=1;j<=cd;j++){if(f[i][j].cnt==inf)continue;f[i+1][j]=min1(f[i+1][j],{f[i][j].sum,f[i][j].cnt,0,j});lll ne=b[i+1]*d[j];lll o=1;ne=gcd(ne,k*o);int nx=id[ne];f[i+1][nx]=min1(f[i+1][nx],{f[i][j].sum+a[i+1],f[i][j].cnt+1,1,j});}}int ans=0;vector<int>id1;id1.clear();if(f[n][cd].cnt==inf){cout<<-1<<"\n";return 0;}int x=n,y=cd;while(x>0){if(f[x][y].used)id1.push_back(x),ans++;y=f[x][y].pre1,x--;}

CF1497D

link

转换为图。

首先对于 $i<j<k$，$c_k-c_j>c_j-c_i$

考虑 $f[i]$ 表示以 $i$ 结尾的得分最大值。

考虑按照路径长度从小到大更新。

具体的，枚举 $i$，然后枚举每一个小于 $i$ 的 $j$，尝试更新 $i,j$。

正确性考一条路径经过的边权单调递增，而我们这样子也是单调递增的，那么肯定是对的。

那么这题就做完了。

代码：

cin>>n;for(int i=1;i<=n;i++)cin>>tag[i];for(int i=1;i<=n;i++)cin>>s[i],f[i]=0;for(int i=1;i<=n;i++)for(int j=i-1;j>=1;j--){if(tag[i]==tag[j])continue;int v=abs(s[i]-s[j]);int di=f[i],dj=f[j];f[i]=max(f[i],dj+v);f[j]=max(f[j],di+v);}int ans=0;for(int i=1;i<=n;i++)ans=max(ans,f[i]);cout<<ans<<"\n";

CF1593G

link

注意到，( 和 ) 没有区别，[ 和 ] 没有区别。

考虑需要代价的情况，可以构造出 [([( 的情况，此时需要 $2$ 的代价。

再看合法情况，考虑到一对合法的匹配，位置上是一奇一偶。

由于 [ 可以转换成 (，所以只需要看 [ 即可。

可以得出，需要改变的 [ 数即为奇数位置上 [ 的数量和偶数位置上 ] 数量的差值。

解释的话可以看图：

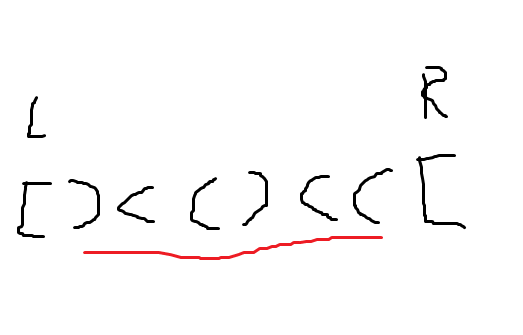
找到 $L$,$R$ 使得中间没有 [，显然如果间隔偶数个，中间的 ( 一定可以两两配对。

中间是奇数个，考虑若这两个无法抵消掉，是多出来的，那么显然只能将它们改写成 ( 来配对。

故这种策略是可行的。

代码：

		cin>>s;int n=s.size();s=" "+s;for(int i=1;i<=n;i++){s[i]=(s[i]==')'?'(':(s[i]==']'?'[':s[i]));s2[i][0]=s2[i-1][0]+((i%2==0)&&(s[i]=='['));s2[i][1]=s2[i-1][1]+((i%2==1)&&(s[i]=='['));}int q;cin>>q;while(q--){int l,r;cin>>l>>r;cout<<abs(s2[r][0]-s2[l-1][0]-s2[r][1]+s2[l-1][1])<<"\n";}