Ackley函数：优化算法领域的复杂试金石

在计算数学和优化理论中，评估算法的性能需要一个能够模拟现实问题复杂性的测试基准。Ackley函数正是这样一个精心设计的数学构造，它以其看似简单却极具欺骗性的表面，成为了优化算法研究领域的标准试金石。这个函数不仅考验着算法寻找全局最优解的能力，更揭示了优化过程中可能遇到的各种陷阱和挑战。

Ackley函数的数学定义展现了一种巧妙的复杂性组合。对于一个$n$维向量$\mathbf{x}=(x_1,x_2,\dots ,x_n)$，函数表达式为：
$$f(\mathbf{x})=-a\cdot \exp \left(-b\sqrt{\frac{1}{n}\sum _{i=1}^n{x}_i^2}\right)-\exp \left(\frac{1}{n}\sum _{i=1}^n\cos (c\cdot x_i)\right)+a+\exp (1)$$
其中参数通常取值为$a=20$，$b=0.2$，$c=2\pi$。这个公式由三个主要部分组成：第一个指数项控制着从中心向外的衰减模式，第二个指数项引入了高频振荡，而常数项$a+\exp (1)$则确保了函数在远离原点时保持正值。

这个函数的全局最小值出现在原点$\mathbf{x}=0$处，此时函数值为$f(0)=0$。然而，找到这个看似简单的最小值却是一项极具挑战性的任务，因为函数在搜索空间中设置了多重障碍。首先，当算法探索远离中心的区域时，会遇到几乎完全平坦的高原，这里的梯度值接近于零，使得基于梯度的优化方法难以找到有效的下降方向。其次，函数表面布满了由余弦项产生的无数局部极小点，这些"陷阱"会误导算法过早收敛到次优解。

为了直观理解Ackley函数的复杂地形，我们可以通过Python可视化其二维版本。以下代码生成了函数的等高线图，清晰展示了其独特的景观特征：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cmdef ackley_2d(x, y, a=20, b=0.2, c=2*np.pi):"""二维Ackley函数实现"""term1 = -a * np.exp(-b * np.sqrt(0.5 * (x**2 + y**2)))term2 = -np.exp(0.5 * (np.cos(c * x) + np.cos(c * y)))return term1 + term2 + a + np.exp(1)# 生成网格数据
x = np.linspace(-5, 5, 400)
y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
Z = ackley_2d(X, Y)# 绘制等高线图
plt.figure(figsize=(10, 8))
contour = plt.contourf(X, Y, Z, levels=50, cmap=cm.viridis)
plt.colorbar(contour, label='Function Value')
plt.contour(X, Y, Z, levels=10, colors='white', linewidths=0.5)
plt.title('Ackley函数二维等高线图', fontsize=14)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.scatter(0, 0, c='red', s=50, label='全局最小值 (0,0)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

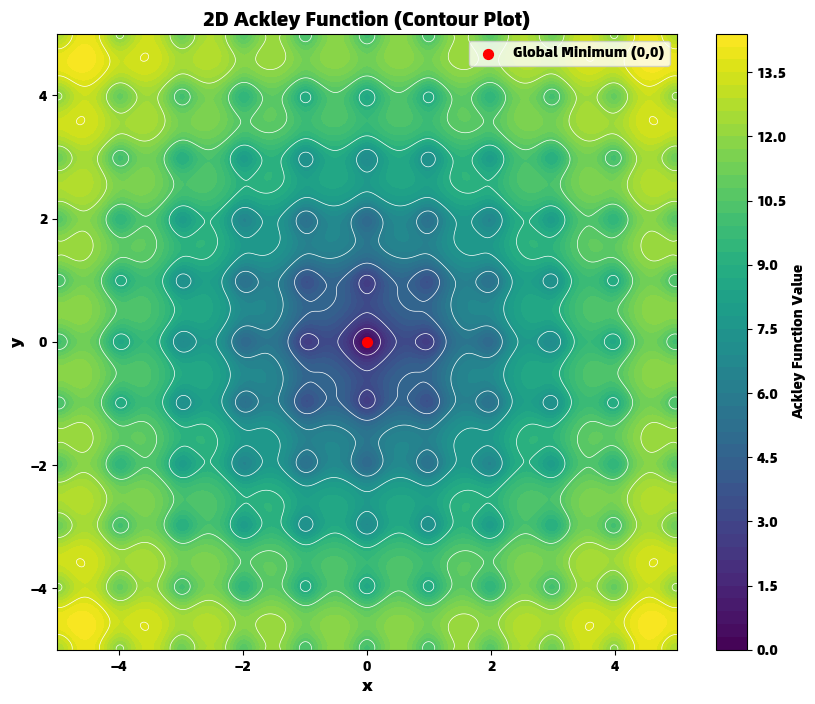
从生成的图像中可以观察到几个关键特征：中心区域的深色部分对应着全局最小值点，周围的同心环状结构显示了函数的振荡特性，而外围的均匀颜色区域则表明了平坦的高原地形。这种视觉表现直观解释了为什么传统优化算法在此函数上表现不佳——它们要么在平坦区域停滞不前，要么被局部极小点所困。

为了更深入地理解Ackley函数的三维几何结构，我们可以创建表面图来展示其立体形态：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
def ackley(x, y, a=20, b=0.2, c=2*np.pi):"""二维 Ackley 函数"""term1 = -a * np.exp(-b * np.sqrt(0.5 * (x**2 + y**2)))term2 = -np.exp(0.5 * (np.cos(c * x) + np.cos(c * y)))return term1 + term2 + a + np.exp(1)
# 创建三维画布
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')# 绘制表面图（为避免过于密集，缩小网格点数）
x_3d = np.linspace(-5, 5, 100)
y_3d = np.linspace(-5, 5, 100)
X_3d, Y_3d = np.meshgrid(x_3d, y_3d)
Z_3d = ackley(X_3d, Y_3d)surf = ax.plot_surface(X_3d, Y_3d, Z_3d, cmap=cm.viridis, rstride=1, cstride=1, alpha=0.8)
fig.colorbar(surf, ax=ax, shrink=0.5, label='Ackley Value')# 标记最小值点
ax.scatter(0, 0, 0, c='red', s=100, label='Global Minimum')ax.set_title('3D Ackley Function', fontsize=14)
ax.set_xlabel('x', fontsize=12)
ax.set_ylabel('y', fontsize=12)
ax.set_zlabel('f(x,y)', fontsize=12)
ax.legend()
plt.show()

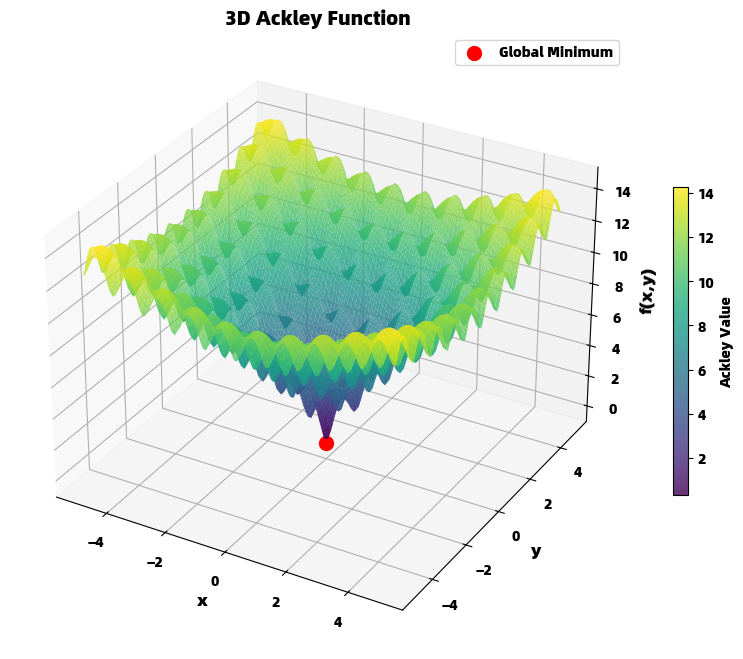
三维可视化进一步揭示了Ackley函数的复杂性。中心处的陡峭"深井"与周围平坦的高原形成鲜明对比，表面上的细微波纹则代表了那些可能困住优化算法的局部极小点。这种结构使得Ackley函数成为测试算法鲁棒性的理想工具。

在实际应用中，研究人员使用Ackley函数来评估各种优化算法的性能。以下是一个使用粒子群优化（PSO）算法求解Ackley函数的示例：

import numpy as np
from scipy.optimize import differential_evolutiondef ackley_nd(x, a=20, b=0.2, c=2*np.pi):"""n维Ackley函数实现"""n = len(x)sum_sq = np.sum(x**2)sum_cos = np.sum(np.cos(c * x))term1 = -a * np.exp(-b * np.sqrt(sum_sq / n))term2 = -np.exp(sum_cos / n)return term1 + term2 + a + np.exp(1)# 使用差分进化算法求解
bounds = [(-5, 5)] * 10  # 10维问题
result = differential_evolution(ackley_nd, bounds, strategy='best1bin',popsize=30, tol=1e-8, mutation=(0.5, 1),recombination=0.7, seed=42)print("优化结果:")
print(f"全局最小值: {result.fun}")
print(f"最优解: {result.x}")
print(f"迭代次数: {result.nit}")
print(f"函数调用次数: {result.nfev}")

这个示例展示了如何使用现代优化算法处理高维Ackley问题。差分进化算法作为一种基于种群的随机优化技术，能够较好地处理多模态和不可微函数，但其性能仍然受到函数复杂性的挑战。

Ackley函数的重要性不仅在于其作为测试基准的实用性，更在于它揭示了优化问题的本质特征。在现实世界的工程优化、机器学习模型训练和科学研究中，我们经常遇到类似Ackley函数的问题景观：高维搜索空间、多模态特性、平坦区域和狭窄的全局最优盆地。例如，在神经网络训练中，损失函数往往包含大量局部极小点，而梯度消失问题则对应于Ackley函数中的平坦区域。

理解Ackley函数的特性有助于我们设计更强大的优化算法。针对其平坦区域，算法需要具备跳出停滞状态的能力；面对局部极小点，算法需要有效的探索机制；而对于狭窄的全局最优区域，算法则需要精细的开发和收敛策略。这些要求推动了模拟退火、遗传算法、粒子群优化等现代优化技术的发展。

随着计算能力的提升和优化理论的进步，Ackley函数继续在新的研究领域中发挥作用。在多目标优化、约束优化和动态优化问题中，研究人员开发了Ackley函数的变体来测试算法的综合性能。这些变体可能包含多个全局最小值、随时间变化的景观或其他复杂特征，为算法评估提供了更加丰富的测试场景。

总之，Ackley函数作为优化算法领域的经典测试问题，其价值不仅在于提供一个难以优化的数学函数，更在于它凝聚了现实世界优化问题的核心挑战。通过研究和理解这个函数，我们能够更好地设计、评估和改进优化算法，最终推动整个领域向前发展。在人工智能和机器学习快速发展的今天，这种基础性的研究工作显得尤为重要，因为它为处理日益复杂的现实问题提供了理论基础和方法论支持。