神经算子学习

一、基本概念

神经算子：用神经网络去近似求解偏微分方程，实际上是在学习一个“算子”，即从一个函数空间A到另一个函数空间B的映射。神经算子可以学习函数空间到函数空间的映射关系，从而实现“一次训练，解决一类PDE”的目标。这意味着，在处理具有多个参数或不用边界条件的PDE类时，只需进行一次的模型训练即可泛化到一类的PDE求解。

函数：从数字空间到数字空间的映射

泛函：从函数空间到数字空间的映射

算子：从函数空间到函数空间的映射

二、神经算子定义与分类

2.1 神经算子的定义

神经算子是一类用于学习函数到函数映射的深度学习模型，适用于偏微分方程（PDE）求解、物理建模、科学计算等问题。与传统神经网络关注“输入到输出”之间的数值映射不同，神经算子的目标是直接近似一个用于描述函数空间之间映射的算子——即输入为函数，输出仍为函数。各种类型的神经算子均以端到端的形式学习逼近输入函数到输出函数两个函数空间之间的映射关系。

2.2 神经算子三大基础结构分类

① 基于通用逼近定理的DeepONet

DeepONet是提出最早也是最基础的一类神经算子，其基本思想是基于通用的函数逼近定理，用神经网络来学习算子映射。换句话说，它学习的是一个“函数到函数”的映射过程：输入是可以控制PDE变化的函数，输出则是PDE的解函数。主要由两部分组成：Branch网络：负责接收初始/边界函数、源项等函数信息；Trunk网络：负责接收空间坐标等“查询点”作为输入。这种设计非常灵活，可以根据不同任务选择不同的网络结构。例如，Branch和Trunk网络可以是普通前馈神经网络（FNN），也可以是卷积网络（CNN）等。

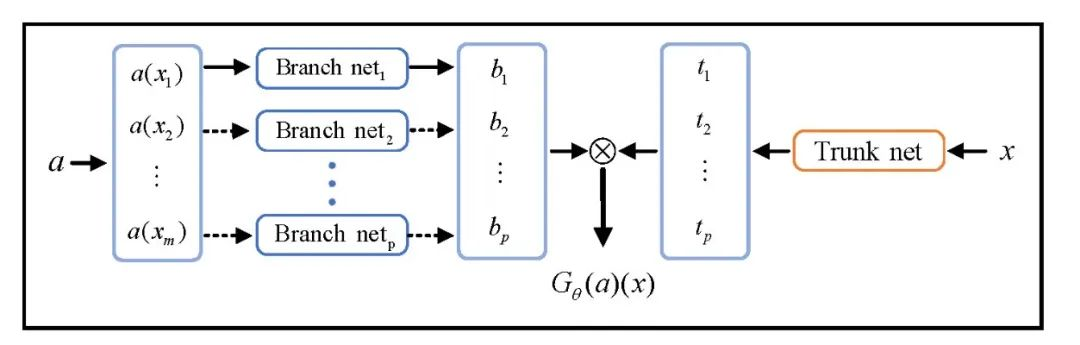
② 基于网格或图结构的积分核型神经算子

积分核神经算子通过组合线性积分算子与逐点非线性激活函数，从而逼近复杂的非线性映射。这种结构本质上是定义在函数空间上的“深层网络”，输入与输出都是函数，不依赖特定的离散化方式。其中，最典型的是傅里叶神经算子（FNO）。其核心思想是：将积分操作通过傅里叶变换在频域中实现，利用快速傅里叶变换进行高效计算，从而提高计算速度和准确率。

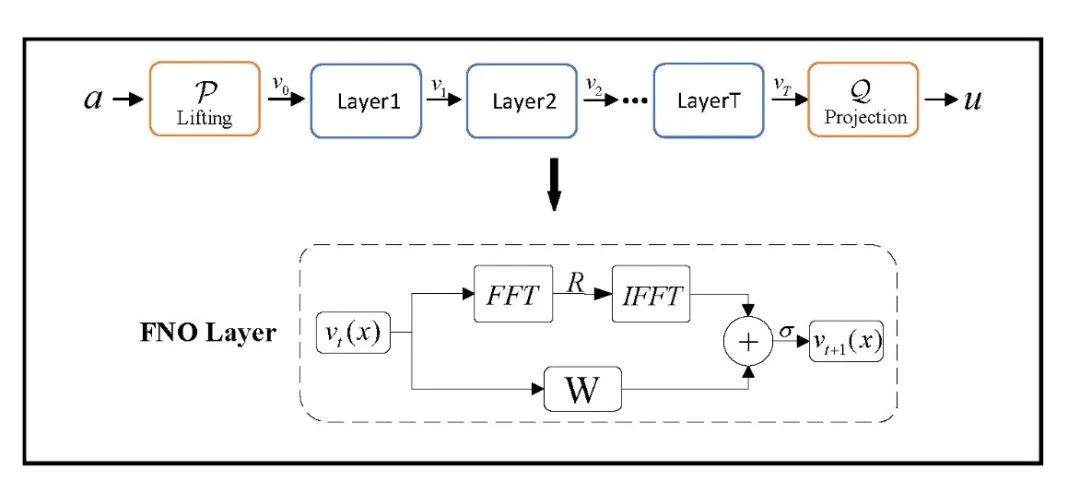
③ 基于Transformer的神经算子

GNOT（General Neural Operator Transformer）架构，GNOT支持任意位置的输入和输出，可处理多个输入函数、不规则网格以及多尺度问题，极大地拓展了神经算子的应用范围。该模型通过交叉注意力、自注意力与门控前馈网络的组合，使得每一步更新都能兼顾输入函数的全局信息与查询点的局部特征，从而实现高效且灵活的算子学习。

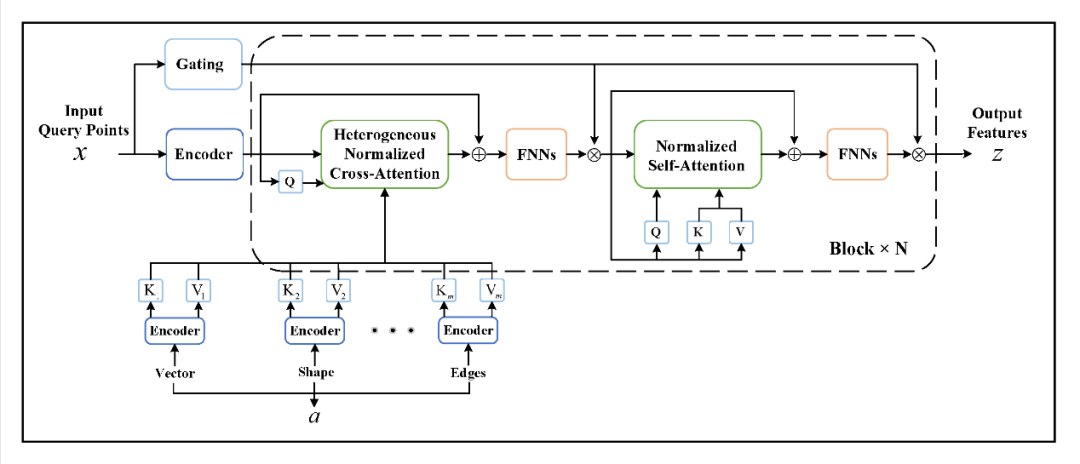
三、神经算子拓展及变体

3.1 基于算子基的变体

基于算子基的神经算子变体主要利用不同的函数基底、扩展基空间或分解技术来增强原有架构的稳定性、灵活性和表达能力。

① 基于不同基函数的变体

受傅里叶神经算子将傅里叶变换引入积分核算子结构中，在频域学习逼近算子映射的启发，众多研究者从基函数出发，拓展设计了新的算子模型。

如：小波神经算子（WNO）用时频双域的小波基替代FNO的全局傅里叶基，不仅保留了多尺度分析能力，还能在非规则网格和突变信号场景中保持鲁棒性。

② 基于算子基分解的扩展

分解式扩展方法通过主算子进行维度或模态分解进一步优化其性能。如：F-FNO对每个空间维度进行独立傅里叶处理，大幅降低复杂度、提高深度网络稳定性。

③ 基于基函数空间的扩展

在基函数空间扩展方向上，通过引入高维编码、潜在空间和新型算子结构来提升算子的表达能力。

如：Improved-DeepONet在分支和主干之间加入两个编码器，将输入映射到高维特征空间，并在网络各层通过点对点融合增强非线性表达。

3.2 融合物理先验的神经算子

基于数据驱动的神经算子对数据质量的依赖度较高，需要大量高质量训练数据的支撑。实际问题中常见三种情形：一是物理信息完备但数据稀缺；二是数据与物理信息均部分可得；三是数据充裕但缺乏物理先验。其中第二种情况最为普遍，也催生了多种混合方法。通过将已知的物理信息（如方程、初始边界条件等）嵌入到损失中，将物理信息约束与数据驱动的神经算子相结合，可以缓解纯数据驱动方法对大量高质量训练数据的依赖。将神经算子的高效性与物理信息的可靠性结合，既能加速求解又能保证精度。

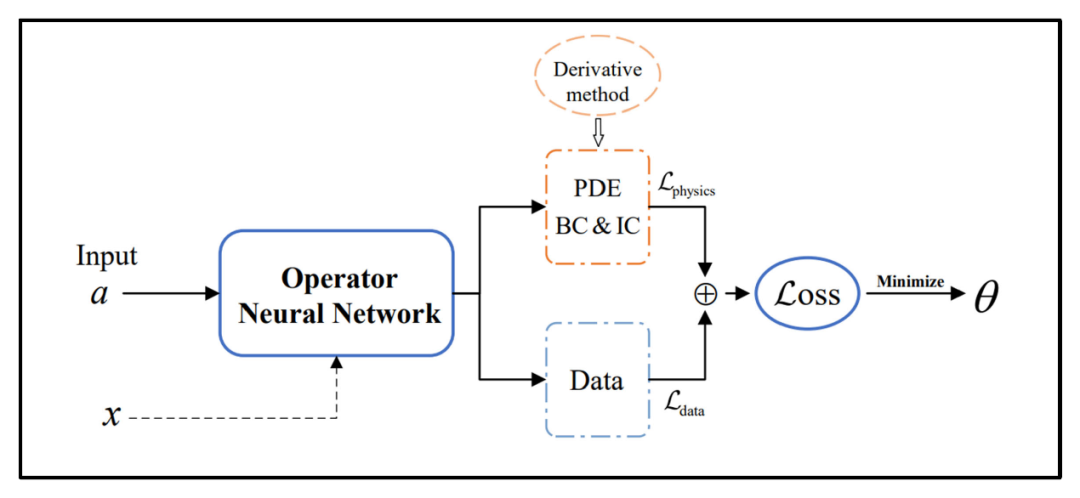
3.3 复杂系统建模

现有工作中，大部分算子方法只是处理了一些简单偏微分方程系统，而复杂系统中的神经算子在实际应用时会面临不规则网格、多尺度和多输入等挑战，同时在不确定性量化、气候科学、工程和生物医药等领域有着广泛应用需求。因此许多算子研究关注这些复杂现实应用，设计了更加有效广泛的算子结构。