Label Smoothing Cross Entropy(标签平滑交叉熵) 是什么
🎯 一、标准交叉熵回顾
对于一个分类任务,假设真实标签是 one-hot 编码:
y=[0,0,...,1,...,0](第 k 位为1)
模型输出 logits 经过 softmax 得到预测概率分布:

标准交叉熵损失(Cross Entropy, CE)为:
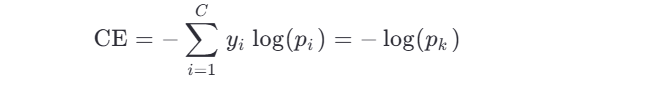
即:只关注真实类别的预测概率,希望它趋近于 1。
🌟 二、Label Smoothing 的思想
真实标签是“非0即1”的硬标签(hard labels),模型在训练后期很容易对正确类别输出接近 1 的概率(如 0.9999),对其他类别接近 0 —— 这会导致:
- 模型过于自信 → 泛化能力下降
- 容易过拟合训练集
- 对抗样本敏感
- 校准(calibration)差:预测概率 ≠ 真实置信度
💡 Label Smoothing 的核心思想:
不让模型“太相信”训练标签是绝对正确的,而是给它一个“软化”的目标分布,让模型对非真实类别也保留一点点概率。
📐 三、Label Smoothing 的数学形式
设类别总数为 C ,平滑系数为 ϵ (通常取 0.1 或 0.2),则平滑后的标签 yiLS 为:
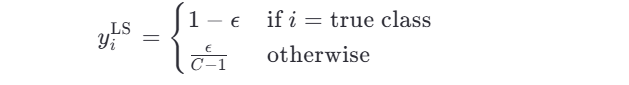
👉 也就是说:
- 真实类别概率从 1 → 1−ϵ
- 其他每个类别从 0 → C−1ϵ
然后使用这个软标签计算交叉熵:
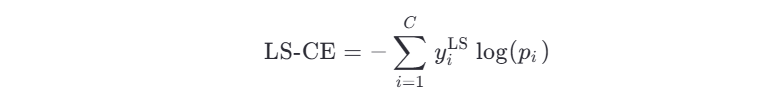
🧠 四、直观理解
举个例子:3分类,真实标签是第2类,ϵ=0.1
- 原始 one-hot 标签:
[0, 1, 0] - 平滑后标签:
[0.05, 0.9, 0.05]
模型不再追求把第2类概率压到1,而是“满足于”0.9;同时,允许其他类别有0.05的概率 —— 这样模型不会“走极端”,泛化更好。
📈 五、优点
- 缓解过拟合:模型不会对训练数据“死记硬背”。
- 提高校准性(calibration):预测概率更接近真实正确率。
- 提升模型鲁棒性:对噪声标签或对抗样本更稳健。
- 常用于大模型:如 Vision Transformer、BERT、ResNet 等都常用 label smoothing。
import torch
import torch.nn as nn
import torch.nn.functional as Fclass LabelSmoothingCrossEntropy(nn.Module):def __init__(self, smoothing=0.1):super(LabelSmoothingCrossEntropy, self).__init__()self.smoothing = smoothingdef forward(self, pred, target):log_probs = F.log_softmax(pred, dim=-1)nll_loss = -log_probs.gather(dim=-1, index=target.unsqueeze(1)).squeeze(1)smooth_loss = -log_probs.mean(dim=-1)loss = (1 - self.smoothing) * nll_loss + self.smoothing * smooth_lossreturn loss.mean()