强化学习笔记(二)多臂老虎机(一)

多臂老虎机

强化学习使用对所采取动作的评价进行训练，而不是通过给出正确动作为指导。这导致其需要主动探索、显式搜索良好行为。

• 评价性反馈：表明所采取动作的好坏，但不说明是否为最优或最差动作。
• 指导性反馈：直接给出正确动作，与实际采取的动作无关。

强化学习使用评价性反馈（evaluative feedback），而非指导性反馈。评价性反馈完全依赖于所采取的动作(不同的动作会有不用的反馈)，而指导性反馈则与所采取的动作无关(不同的动作会有相同的反馈)。这部分中只研究强化学习的评价性特征，在一个简化场景中进行，该场景为非关联性问题，不涉及在多种情境下学习如何行动。

[!NOTE]

想象你面前有多个老虎机（比如10台），每台机器拉下拉杆后会以某种未知概率给你不同金额的奖励。你的目标是在有限次数的拉杆操作中，最大化总奖励。

但问题是：你不知道每台机器的真实收益分布 —— 有些机器可能回报高，有些可能回报低。

k臂老虎机问题可以定义为面临 k 个不同动作（或选项）的重复选择；每次选择一个动作后，获得一个数值奖励；奖励来自依赖于所选动作的平稳概率分布，你的目标是在有限时间步（如1000步）内，最大化累计奖励的期望值。当前的“老虎机问题”特指此简单非关联性情形，不涉及状态变化。

动作价值

每个动作 a 有一个真实价值 $ q_*(a) $，定义为选择该动作时的期望奖励：
$$q_{\ast }(a)\doteq \mathbb{E}[R_t\mid A_t=a]$$

• $ A_t $：时间步 $ t $ 选择的动作
• $ R_t $：时间步 $ t $ 获得的奖励

当前动作价值的真实价值未知，需进行估计。用 $ Q_t(a) $ 表示在时间步 $ t $ 时对动作 a 的价值估计。当前的目标是使 $ Q_t(a) $ 尽可能接近 $ q_*(a) $。

贪婪动作、探索与价值

当前时间步估计价值最高的动作被称为贪婪动作。由此我们可以引出利用和探索的定义。利用是选择贪婪动作，以最大化当前步的期望奖励。探索是选择非贪婪动作，以改进其价值估计。探索短期收益低，但可能发现更优动作，长期收益更高。探索与利用之间存在冲突，何时探索或利用，取决于估计值的精度、不确定性大小、剩余时间步数。

动作价值方法

动作价值方法指用于估计动作价值并基于估计进行动作选择的一类方法。动作的价值的真实值是选择这个动作时的期望收益。

估计价值

样本平均法通过计算实际收益的平均值来估计动作的价值：
$$Q_t(a)\doteq \frac{\text{在 }t\text{ 前选择 }a\text{ 所获奖励之和}}{\text{在 }t\text{ 前选择 }a\text{ 的次数}}=\frac{{\sum }_{i=1}^{t-1}{R}_i\cdot 1_{A_i=a}}{{\sum }_{i=1}^{t-1}{1}_{A_i=a}}$$

• 其中 $1_{predicate}$ 表示一个随机变量，当 predicate 为真时取值为1，否则为0。
• 若分母为0，定义 $ Q_t(a) $ 为默认值（如0）。
• 根据大数定律，当选择次数趋于无穷时，$ Q_t(a) \to q_*(a) $。

贪婪动作选择

贪婪动作选择指的是选择当前估计价值最高的动作：
$$A_t\doteq \underset{a}{\mathrm{argmax}}{Q}_t(a)$$
若有多个最大值，任意选择（如随机）。其始终利用当前知识，最大化即时奖励。存在不探索，可能错过更优动作的缺点。

对贪心策略的优化

一种优化方法是大多数时间选择贪婪动作；以小概率 $ \varepsilon $​，随机均匀选择所有动作（包括贪婪动作），与估计值无关，从而实现探索与利用的平衡。这个方法的优点是，随着步数趋于无穷，每个动作都会被无限次采样，从而确保所有 $Q_t(a)$ 收敛到 $q_{\ast }(a)$。这意味着选择最优动作的概率将收敛到大于 $1-\epsilon$ 的值，即接近确定。然而，这些只是渐近性保证，对于方法在实际中的有效性说明有限。

练习2.1

在 ε-贪婪动作选择中，在有两个动作及 ε = 0.5 的情况下，贪婪动作被选择的概率是多少？

在 ε-贪婪策略中：

• 以概率 1 - ε，选择当前估计价值最高的动作（即贪婪动作） → 利用
• 以概率 ε，从所有 k 个动作中均匀随机选择一个动作 → 探索

注意：在“探索”阶段，即使选中了当前的贪婪动作，那也是随机选中的，不是因为它是贪婪动作。

• 动作数量：k = 2
• ε = 0.5

贪婪动作可以在两种情况下被选中：

1. 利用阶段（概率 = 1 - ε = 0.5） → 一定选择贪婪动作
   → 贡献概率：0.5 × 1 = 0.5

2. 探索阶段（概率 = ε = 0.5） → 随机均匀选择两个动作中的一个
   → 贪婪动作被随机选中的概率 = 1/2
   → 贡献概率：**0.5 × (1/2) = 0.2

$$P(\text{选择贪婪动作})=0.5+0.25=\boxed{0.75}$$

在 ε = 0.5 且有两个动作的情况下，贪婪动作被选择的概率是 0.75。

实验一

为评估贪婪方法与 $\epsilon$-贪婪方法的性能，将使用 样本平均法 估计动作价值，并在 2000 个随机生成的 10 臂老虎机问题 上，每个问题运行 1000 步，最后报告：

1. 平均奖励随时间步的变化曲线
2. 最优动作选择比例随时间步的变化曲线

其中

• 每个动作的真实价值 $ q_*(a) $ 从均值为0、方差为1的正态分布中随机生成；
• 每次选择动作后，实际奖励 $ R_t $ 从均值为 $ q_*(A_t) $、方差为1的正态分布中采样。
  
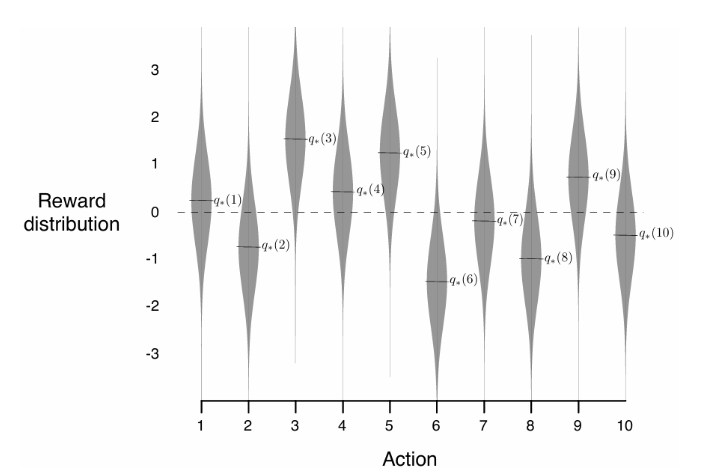
  图2.1： 十个动作中每个动作的真实值 $q_{\ast }(a)$ 是根据均值为0、方差为1的正态分布选取的，随后实际奖励根据均值为 $q_{\ast }(a)$、方差为1的正态分布选取，如灰色分布所示。

import numpy as np
import matplotlib.pyplot as pltk = 10                  # 臂的数量
n_steps = 1000          # 每个任务的时间步数
n_problems = 2000       # 任务数量
epsilons = [0.0, 0.01, 0.1]  # 不同的 epsilon 值# rewards、optimal_actions 是典，键是eps，值是形状为 (2000, 1000)的NumPy数组。
rewards = {eps: np.zeros((n_problems, n_steps)) for eps in epsilons}
optimal_actions = {eps: np.zeros((n_problems, n_steps)) for eps in epsilons}# 主循环 进行两千次实验
for problem_idx in range(n_problems):# 生成当前问题的真实动作价值 q*(a) ~ N(0, 1)true_q = np.random.randn(k)best_action = np.argmax(true_q)  # 最优动作# 对每个 epsilon 策略进行实验for eps in epsilons:# 初始化估计值 Q(a) 和选择次数 N(a)Q = np.zeros(k)N = np.zeros(k)for t in range(n_steps):# ε-贪婪动作选择if np.random.rand() < eps:action = np.random.randint(k)  # 探索：随机选动作else:action = np.argmax(Q)          # 利用：选当前最优# 记录是否选择了最优动作optimal_actions[eps][problem_idx, t] = 1 if action == best_action else 0# 生成奖励 R ~ N(q*(a), 1)reward = np.random.randn() + true_q[action]rewards[eps][problem_idx, t] = reward# 增量更新 Q(a)N[action] += 1Q[action] += (reward - Q[action]) / N[action]# 计算平均结果
avg_rewards = {eps: np.mean(rewards[eps], axis=0) for eps in epsilons}
avg_optimal = {eps: np.mean(optimal_actions[eps], axis=0) for eps in epsilons}# 绘图
plt.figure(figsize=(12, 8))# 上图：平均奖励
plt.subplot(2, 1, 1)
for eps in epsilons:label = f"ε = {eps}" if eps > 0 else "Greedy (ε = 0)"plt.plot(avg_rewards[eps], label=label)
plt.title("10-Armed Testbed: Average Reward over Time")
plt.xlabel("Time Step")
plt.ylabel("Average Reward")
plt.legend()
plt.grid(True)# 下图：最优动作选择比例
plt.subplot(2, 1, 2)
for eps in epsilons:label = f"ε = {eps}" if eps > 0 else "Greedy (ε = 0)"plt.plot(avg_optimal[eps], label=label)
plt.title("10-Armed Testbed: % Optimal Action over Time")
plt.xlabel("Time Step")
plt.ylabel("% Optimal Action")
plt.legend()
plt.grid(True)plt.tight_layout()
plt.savefig("10_arm_testbed_results.png", dpi=300)
plt.show()

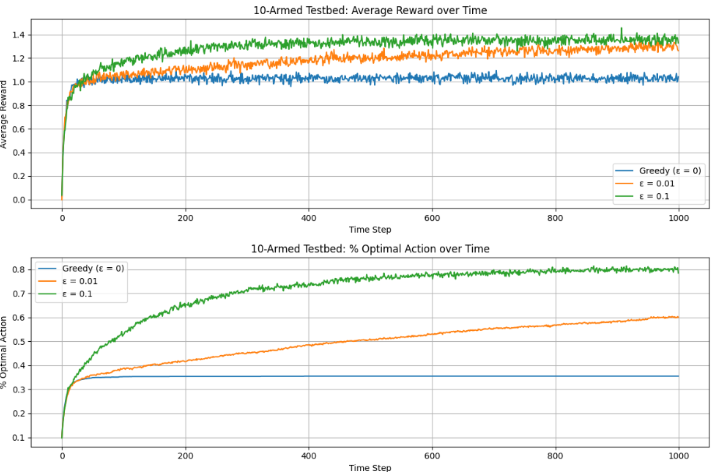
图2.2：比较了贪婪方法与两种$\epsilon$-贪婪方法（$\epsilon =0.01$ 和 $\epsilon =0.1$）在10臂测试平台上的表现。所有方法均使用样本平均法来估计动作价值。上图显示了期望奖励随经验增长的情况。贪婪方法在最开始略微提升更快，但随后趋于平稳，且稳定在较低水平。其每步平均奖励仅为约1，而该测试平台上的最优可能值约为1.55。贪婪方法在长期表现较差，因为它常常陷入执行次优动作的情况。

主要结果：

• 贪婪方法：

  • 初期提升较快，但很快陷入局部最优；
  • 在约三分之二的任务中未能识别最优动作；
  • 长期平均每步奖励约为1（远低于最优值约1.55）；
  • 因缺乏探索，常被次优动作“锁定”。

• $\epsilon$-贪婪方法：

  • 通过持续探索，能更可靠地发现最优动作；
  • $\epsilon =0.1$：探索频繁，更快找到最优动作，但最多仅以91%的概率选择最优动作；
  • $\epsilon =0.01$：探索较少，初期进展慢，但长期性能优于 $\epsilon =0.1$；
  • 可通过随时间降低 $\epsilon$ 来兼顾探索与利用。

关键结论：

• $\epsilon$-贪婪方法在长期表现上显著优于纯贪婪方法；
• 探索的重要性取决于任务特性：
  • 奖励噪声越大（方差高），越需要探索；
  • 即使在确定性环境中，若任务非平稳（动作价值随时间变化），探索仍必不可少；
• 在强化学习中，由于策略演化导致决策任务动态变化，探索与利用的平衡是必要且普遍的要求。

练习 2.2

题目：
考虑一个 k = 4 的多臂赌博机问题，记作动作 1、2、3、4。
算法使用 ε-贪婪动作选择，基于采样平均的动作价值估计，初始估计 $ Q_1(a) = 0, \forall a $。
假设动作及收益的最初顺序是：
$ A_1 = 1, R_1 = -1 $
$ A_2 = 2, R_2 = 1 $
$ A_3 = 2, R_3 = -2 $
$ A_4 = 2, R_4 = 2 $
$ A_5 = 3, R_5 = 0 $

问：在哪些时刻中，肯定发生了随机探索（即 ε 情形）？在哪些时刻中，可能发生？

• 初始时，所有 $ Q_1(a) = 0 $，所以第 1 步时所有动作价值相等 → 任意动作都是“贪婪动作”。
• ε-贪婪策略：以概率 $ 1 - \varepsilon $ 选择当前估计最优动作（若有多个，可任选其一）；以概率 $ \varepsilon $ 随机选动作。
• 关键：只有当所选动作不是当前估计最优动作时，才“肯定”是探索。
  如果所选动作是当前最优动作，则可能是利用（大概率），也可能是探索时“碰巧”选中了最优动作（小概率）。

我们用采样平均法更新 $ Q_t(a) $：

时间步 t=1：

• 选 $ A_1 = 1 $，得 $ R_1 = -1 $
• 所有 Q 初始为 0 → 任意动作都是贪婪动作 → 选动作 1 可以是利用（任意选一个最优），也可以是探索
• 结论：可能发生了探索（不能肯定）

更新后：

• $ Q_2(1) = -1 $，其余仍为 0

时间步 t=2：

• 当前估计：
  • Q(1) = -1
  • Q(2)=Q(3)=Q(4)=0 → 最优动作是 {2,3,4}（任选其一）
• 实际选 $ A_2 = 2 $ → 是当前最优动作之一
• 结论：可能是利用（选了最优），也可能是探索时碰巧选中 → 不能肯定发生了探索

更新后：

• $ Q_3(2) = 1 $（第一次选动作 2，直接赋值）
• Q(1) = -1，Q(3)=Q(4)=0

时间步 t=3：

• 当前估计：
  • Q(1) = -1
  • Q(2) = 1 ← 最优！
  • Q(3)=Q(4)=0
• 实际选 $ A_3 = 2 $ → 是当前唯一最优动作
• 所以：如果是利用，一定选 2；如果是探索，有 1/4 概率选 2
• 结论：不能肯定发生了探索（可能是利用，也可能是探索碰巧）

更新后（动作 2 第二次被选）：

• $ Q_4(2) = \frac{1 + (-2)}{2} = -0.5 $

时间步 t=4：

• 当前估计：
  • Q(1) = -1
  • Q(2) = -0.5
  • Q(3)=Q(4)=0 → 最优动作是 {3,4}
• 实际选 $ A_4 = 2 $ → 不是最优动作
• 关键点：只有探索阶段才会选择非贪婪动作
• 结论：肯定发生了探索（ε情形）

更新后：

• 动作 2 第三次被选：$ Q_5(2) = \frac{1 + (-2) + 2}{3} = \frac{1}{3} ≈ 0.333 $

时间步 t=5：

• 当前估计：
  • Q(1) = -1
  • Q(2) ≈ 0.333
  • Q(3)=Q(4)=0 → 最优动作是 {2}（唯一最大）
• 实际选 $ A_5 = 3 $ → 不是最优动作
• 结论：肯定发生了探索

肯定发生了探索（ε情形）的时刻：
t = 4 和 t = 5

可能发生了探索的时刻：
t = 1, 2, 3

增量实现

在强化学习中，动作价值方法通过估计每个动作的期望奖励来指导决策。最直接的方式是将动作价值 $ Q(a) $ 估计为该动作所获得奖励的样本平均值。但若每次更新都重新计算所有历史奖励的平均值，会导致：内存消耗随时间增长和每步计算量逐渐增加因此引入增量更新。

设某动作被选择 $ n-1 $ 次后，其价值估计为：

$$Q_n=\frac{R_1+R_2+\cdots +R_{n-1}}{n-1}$$

当第 $ n $ 次选择该动作并获得奖励 $ R_n $ 后，新的估计应为：

$$Q_{n+1}=\frac{1}{n}\sum _{i=1}^n{R}_i$$

将其改写为仅依赖旧估计 $ Q_n $ 和新奖励 $ R_n $ 的形式：

$$\begin{array}{rl}{Q}_{n+1}& =\frac{1}{n}\left(R_n+\sum _{i=1}^{n-1}{R}_i\right)\\ & =\frac{1}{n}\left(R_n+(n-1)\cdot \frac{1}{n-1}\sum _{i=1}^{n-1}{R}_i\right)\\ & =\frac{1}{n}\left(R_n+(n-1)Q_n\right)\\ & =\frac{1}{n}\left(R_n+n{Q}_n-Q_n\right)\\ & =Q_n+\frac{1}{n}(R_n-Q_n)\end{array}$$

$$\boxed{Q_{n+1}=Q_n+\frac{1}{n}[R_n-Q_n]}\text{\hspace{1em}(2.3)}$$

即使 $ n = 1 $，公式也成立（此时 $ Q_2 = R_1 $，无论初始 $ Q_1 $ 是什么）。

---

通用更新形式

公式 (2.3) 属于一个更广泛的学习模式：

$$\boxed{\text{新估计值}\leftarrow \text{旧估计值}+\alpha \times [\text{目标}-\text{旧估计值}]}\text{\hspace{1em}(2.4)}$$

其中：

• $[\text{目标}-\text{旧估计值}]$：称为误差项（error），表示当前估计与新信息之间的差距
• $\alpha$：步长参数（step-size），控制更新幅度。通常记作 $ \alpha $ 或 $ \alpha_t(a) $，表示在时间 $ t $ 对动作 $ a $ 使用的步长

在样本平均法中，$\alpha =\frac{1}{n}$，即随着观测次数增加，每次更新的影响逐渐减小。

多臂老虎机伪代码

使用增量样本平均法 + $\epsilon$-贪婪策略

初始化：对每个动作 a ∈ {1, 2, ..., k}：Q(a) ← 0          // 动作价值估计N(a) ← 0          // 动作 a 被选择的次数重复执行（每一步）：以概率 1−ε：A ← argmax_{a} Q(a)    // 选择估计价值最高的动作（打破平局随机）以概率 ε：A ← 随机选择一个动作  // 从所有动作中均匀随机选择R ← bandit(A)              // 执行动作 A，获得奖励N(A) ← N(A) + 1            // 更新动作 A 的选择次数Q(A) ← Q(A) + (1 / N(A)) × [R − Q(A)]   // 增量更新价值估计

非平稳问题

指数近期加权平均

在实际强化学习任务中，大多数问题是非平稳的，因此需要能适应变化的估值方法。

类型	定义	特点
平稳问题（Stationary）	动作的真实价值 $ q_*(a) $ 不随时间变化	可使用样本平均法（sample average）有效估计
非平稳问题（Nonstationary）	动作的真实价值 $ q_*(a) $ 随时间变化	样本平均法效果差，需更关注近期奖励

[!NOTE]

在样本平均法中，$\alpha =\frac{1}{n}$，即随着观测次数增加，每次更新的影响逐渐减小。
$$\boxed{Q_{n+1}=Q_n+\frac{1}{n}[R_n-Q_n]}\text{\hspace{1em}(2.3)}$$

为了更好地应对非平稳环境，给予近期奖励比远期奖励更高的权重，引入固定步长参数 $ \alpha \in (0,1] $ 的更新方式：

$$Q_{n+1}=Q_n+\alpha \left[R_n-Q_n\right]\text{\hspace{1em}(2.5)}$$

这相当于对历史奖励进行加权平均，但更重视最近的奖励，就是指数近期加权平均

$$\begin{array}{rl}{Q}_{n+1}& =Q_n+\alpha [R_n-Q_n]\\ & =\alpha R_n+(1-\alpha )Q_n\\ & =\alpha R_n+(1-\alpha )[\alpha R_{n-1}+(1-\alpha )Q_{n-1}]\\ & =\alpha R_n+(1-\alpha )\alpha R_{n-1}+(1-\alpha {)}^2{Q}_{n-1}\\ & =\alpha R_n+(1-\alpha )\alpha R_{n-1}+(1-\alpha {)}^2\alpha R_{n-2}+\cdots \\ & +(1-\alpha {)}^{n-1}\alpha R_1+(1-\alpha {)}^n{Q}_1\\ & =(1-\alpha {)}^n{Q}_1+\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}{R}_i.\end{array}\text{\hspace{1em}(2.6)}$$

• $ R_i $：第 $ i $ 次获得的奖励
• 权重为：$ w_i = \alpha (1 - \alpha)^{n-i} $
• 初始估计 $ Q_1 $ 的权重为：$ (1 - \alpha)^n $

权重的性质

• 所有权重之和为 1：
  $$(1-\alpha {)}^n+\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}=1$$

  [!NOTE]

  总权重：

  $$\text{Total Weight}=(1-\alpha {)}^n+\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}$$

  先处理求和部分：

  令 $ k = n - i $，当 $ i = 1 $ 时，$ k = n - 1 $；当 $ i = n $ 时，$ k = 0 $

  所以：
  $$\sum _{i=1}^n(1-\alpha {)}^{n-i}=\sum _{k=0}^{n-1}(1-\alpha {)}^k$$

  回忆等比数列求和公式：
  $$\sum _{k=0}^m{r}^k=\frac{1-r^{m+1}}{1-r},\text{for }r\ne 1$$

  这里 $ r = 1 - \alpha \in [0, 1) $（因为 $ \alpha \in (0,1] $），所以可以使用公式：

  $$\sum _{k=0}^{n-1}(1-\alpha {)}^k=\frac{1-(1-\alpha {)}^n}{1-(1-\alpha )}=\frac{1-(1-\alpha {)}^n}{\alpha }$$

  现在乘上前面的 $ \alpha $：

  $$\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}=\alpha \cdot \sum _{k=0}^{n-1}(1-\alpha {)}^k=\alpha \cdot \frac{1-(1-\alpha {)}^n}{\alpha }=1-(1-\alpha {)}^n$$

  代入原式：

  $$(1-\alpha {)}^n+\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}=(1-\alpha {)}^n+\left[1-(1-\alpha {)}^n\right]=1$$

  得证

• 权重随时间呈指数衰减

• 越早的奖励（$ i \ll n $），权重越小

• 近期奖励影响更大 → 更适合动态变化环境

变步长参数和收敛

令 $ \alpha_n(a) $ 表示在第 $ n $ 次选择动作 $ a $ 后处理所获奖励时使用的步长参数。

要保证估计值以概率 1 收敛到真实值，需满足：

$$\sum _{n=1}^{\infty }{\alpha }_n(a)=\infty \text{且}\sum _{n=1}^{\infty }{\alpha }_n^2(a)<\infty \text{\hspace{1em}(2.7)}$$

条件	含义
$ \sum \alpha_n = \infty $	保证步长足够大，步长总和发散 → 能克服初始偏差或噪声
$ \sum \alpha_n^2 < \infty $	平方和收敛 → 步长最终足够小，防止震荡

练习 2.4

当步长参数 ${\alpha }_n$ 不是常数时，估计值 $Q_n$ 是对之前所有收益 $R_i$ 的加权平均。要求给出每个历史收益 $R_i$ 在 $Q_n$ 中的权重公式，并推广标准形式（即常数步长）的情况。

已知：

$$Q_{k+1}=Q_k+{\alpha }_k(R_k-Q_k)$$

$$Q_1=Q_1(\text{初始估计})$$

$$Q_2=Q_1+{\alpha }_1(R_1-Q_1)=(1-{\alpha }_1)Q_1+{\alpha }_1{R}_1$$

$$Q_3=Q_2+{\alpha }_2(R_2-Q_2)=(1-{\alpha }_2)Q_2+{\alpha }_2{R}_2=(1-{\alpha }_2)\left[(1-{\alpha }_1)Q_1+{\alpha }_1{R}_1\right]+{\alpha }_2{R}_2$$

$$Q_3=(1-{\alpha }_1)(1-{\alpha }_2)Q_1+{\alpha }_1(1-{\alpha }_2)R_1+{\alpha }_2{R}_2$$

可以看出：

• $R_1$ 的系数是：${\alpha }_1(1-{\alpha }_2)$
• $R_2$ 的系数是：${\alpha }_2$

使用数学归纳法证明以下通项公式成立：

$$Q_n=\left(\prod _{j=1}^{n-1}(1-{\alpha }_j)\right)Q_1+\sum _{i=1}^{n-1}\left({\alpha }_i\prod _{j=i+1}^{n-1}(1-{\alpha }_j)\right)R_i$$

n = 2时有
$$Q_2=(1-{\alpha }_1)Q_1+{\alpha }_1{R}_1$$

代入公式右边：
$$\prod _{j=1}^1(1-{\alpha }_j)=1-{\alpha }_1,\sum _{i=1}^1{\alpha }_i\prod _{j=i+1}^1(1-{\alpha }_j)={\alpha }_1\cdot 1={\alpha }_1$$

所以：
$$Q_2=(1-{\alpha }_1)Q_1+{\alpha }_1{R}_1成立。$$

假设对于某个 $k\ge 2$，有：

$$Q_k=\left(\prod _{j=1}^{k-1}(1-{\alpha }_j)\right)Q_1+\sum _{i=1}^{k-1}\left({\alpha }_i\prod _{j=i+1}^{k-1}(1-{\alpha }_j)\right)R_i$$

由递推关系：
$$Q_{k+1}=Q_k+{\alpha }_k(R_k-Q_k)=(1-{\alpha }_k)Q_k+{\alpha }_k{R}_k$$

将归纳假设代入：

$$Q_{k+1}=(1-{\alpha }_k)\left[\left(\prod _{j=1}^{k-1}(1-{\alpha }_j)\right)Q_1+\sum _{i=1}^{k-1}\left({\alpha }_i\prod _{j=i+1}^{k-1}(1-{\alpha }_j)\right)R_i\right]+{\alpha }_k{R}_k$$

分别处理两个部分：

$$(1-{\alpha }_k)\prod _{j=1}^{k-1}(1-{\alpha }_j)=\prod _{j=1}^k(1-{\alpha }_j)$$

$$(1-{\alpha }_k)\sum _{i=1}^{k-1}\left({\alpha }_i\prod _{j=i+1}^{k-1}(1-{\alpha }_j)\right)R_i=\sum _{i=1}^{k-1}\left({\alpha }_i\prod _{j=i+1}^k(1-{\alpha }_j)\right)R_i$$

再加上 ${\alpha }_k{R}_k$ 这一项：

$$Q_{k+1}=\left(\prod _{j=1}^k(1-{\alpha }_j)\right)Q_1+\sum _{i=1}^k\left({\alpha }_i\prod _{j=i+1}^k(1-{\alpha }_j)\right)R_i$$

因此，对于任意非恒定步长序列 {αn}\{\alpha_n\}{αn​}，收益 $R_i$ 在 $Q_n$ 中的权重为：

$$w_i^{(n)}={\alpha }_i\cdot \prod _{j=i+1}^{n-1}(1-{\alpha }_j),i=1,2,...,n-1$$

特别地，当所有 ${\alpha }_j=\alpha$（常数），则：

$$w_i^{(n)}=\alpha (1-\alpha {)}^{n-1-i}$$

这正是公式 (2.6) 的形式。

练习 2.5

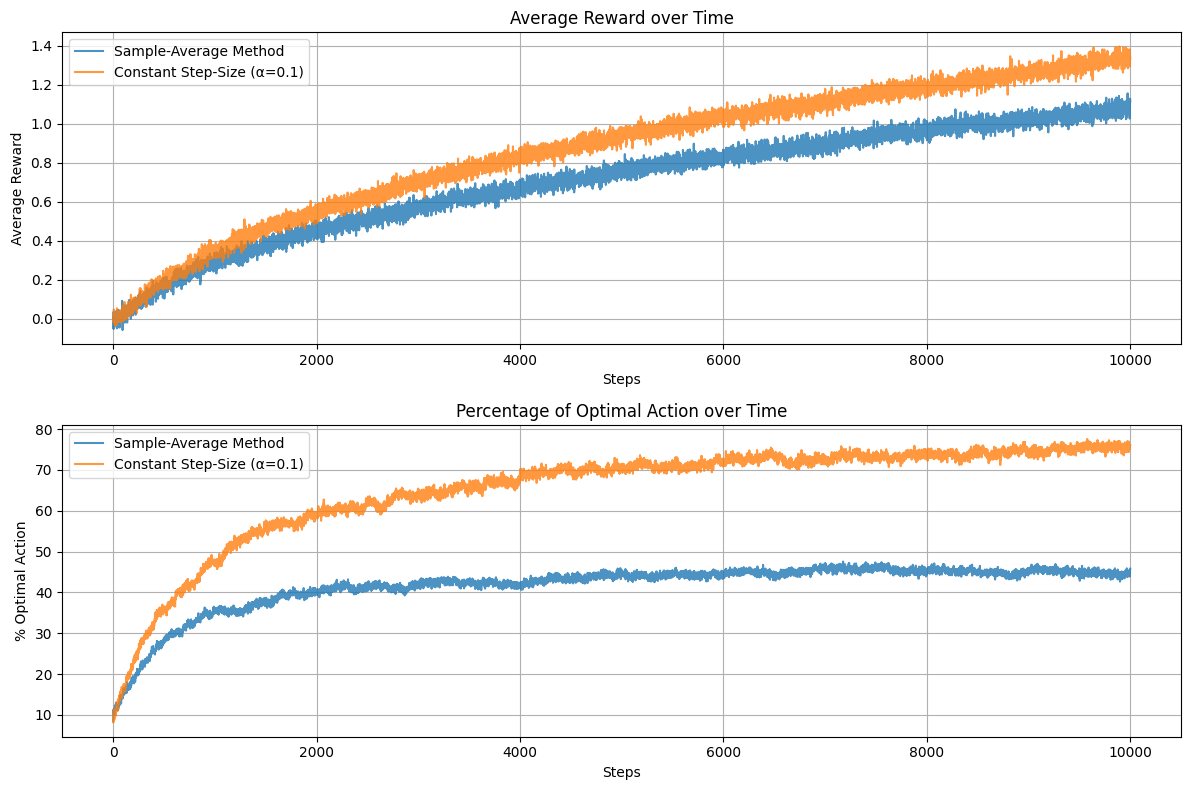
设计并且实施一项实验来证实采用采样平均方法去解决非平稳问题的困难。使用一个 10 臂测试平台的修改版本，其中所有的 $q_{\ast }(a)$ 初始时相等，然后进行随机游走（例如，在每一步所有 $q_{\ast }(a)$ 都加上一个均值为 0、标准差为 0.01 的正态分布增量）。为其中一个方法使用采样平均（增量式计算）的动作-价值估计，为另一个方法使用常数步长参数（$\alpha =0.1$）的动作-价值估计。绘制如图 2.2 所示的分析曲线（平均奖励与最优动作选择百分比随时间步的变化）。采用 $\epsilon =0.1$ 的 $\epsilon$-贪婪策略，并运行足够长的时间（如 10,000 步）。

import numpy as np
import matplotlib.pyplot as plt# 参数设置
k = 10                    # 臂数
epsilon = 0.1             # ε-greedy 探索率
alpha = 0.1               # 常数步长
steps = 10000             # 每次实验运行步数
runs = 2000               # 独立实验次数
q_star_std = 0.01         # 真值随机游走的标准差# 初始化记录数组
rewards_sample_avg = np.zeros(steps)
optimal_actions_sample_avg = np.zeros(steps)rewards_const_alpha = np.zeros(steps)
optimal_actions_const_alpha = np.zeros(steps)# 开始实验
for run in range(runs):if run % 100 == 0:print(f"Run {run}/{runs}")# 初始化真值q_star = np.zeros(k)# 方法1：采样平均Q1 = np.zeros(k)N1 = np.zeros(k, dtype=int)# 方法2：常数步长Q2 = np.zeros(k)for t in range(steps):# 真值随机游走q_star += np.random.normal(0, q_star_std, k)# 找当前最优动作optimal_action = np.argmax(q_star)# 采样平均if np.random.rand() < epsilon:action1 = np.random.randint(k)else:action1 = np.argmax(Q1)# 获取奖励reward1 = np.random.normal(q_star[action1], 1)# 更新计数和估计N1[action1] += 1Q1[action1] += (1 / N1[action1]) * (reward1 - Q1[action1])# 记录rewards_sample_avg[t] += reward1if action1 == optimal_action:optimal_actions_sample_avg[t] += 1# 常数步长 α=0.1 if np.random.rand() < epsilon:action2 = np.random.randint(k)else:action2 = np.argmax(Q2)# 获取奖励reward2 = np.random.normal(q_star[action2], 1)# 更新估计Q2[action2] += alpha * (reward2 - Q2[action2])# 记录rewards_const_alpha[t] += reward2if action2 == optimal_action:optimal_actions_const_alpha[t] += 1# 计算平均值
rewards_sample_avg /= runs
optimal_actions_sample_avg /= runs
optimal_actions_sample_avg *= 100  # 转换为百分比rewards_const_alpha /= runs
optimal_actions_const_alpha /= runs
optimal_actions_const_alpha *= 100# 绘图
fig, ax = plt.subplots(2, 1, figsize=(12, 8))# 平均奖励
ax[0].plot(rewards_sample_avg, label='Sample-Average Method', alpha=0.8)
ax[0].plot(rewards_const_alpha, label='Constant Step-Size (α=0.1)', alpha=0.8)
ax[0].set_xlabel('Steps')
ax[0].set_ylabel('Average Reward')
ax[0].legend()
ax[0].set_title('Average Reward over Time')
ax[0].grid(True)# 最优动作百分比
ax[1].plot(optimal_actions_sample_avg, label='Sample-Average Method', alpha=0.8)
ax[1].plot(optimal_actions_const_alpha, label='Constant Step-Size (α=0.1)', alpha=0.8)
ax[1].set_xlabel('Steps')
ax[1].set_ylabel('% Optimal Action')
ax[1].legend()
ax[1].set_title('Percentage of Optimal Action over Time')
ax[1].grid(True)plt.tight_layout()
plt.show()