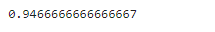人工智能机器学习——决策树、异常检测、主成分分析(PCA)
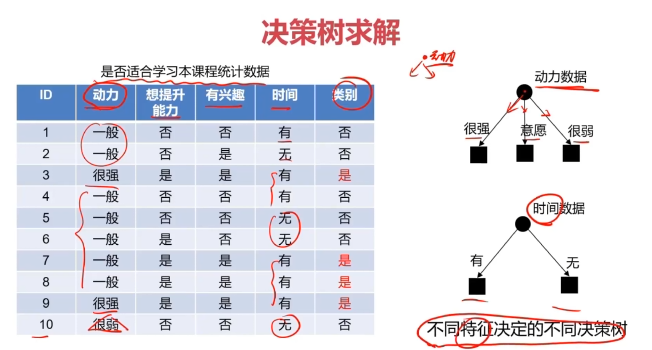
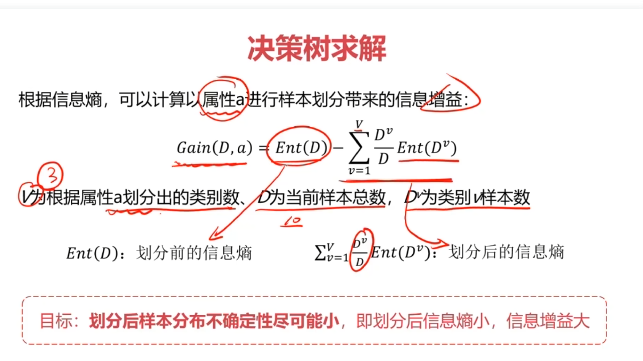
一、决策树(Decision Tree)
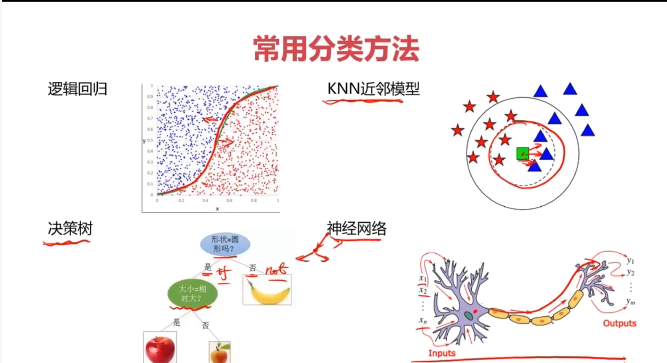
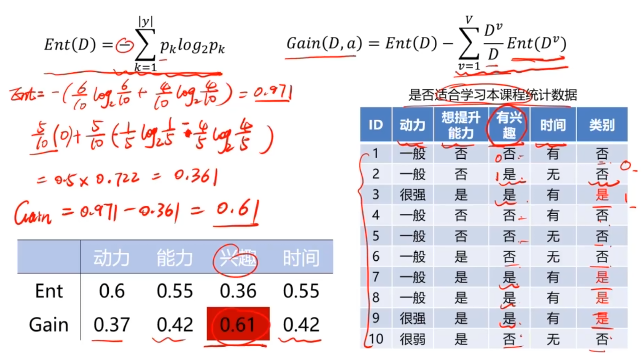
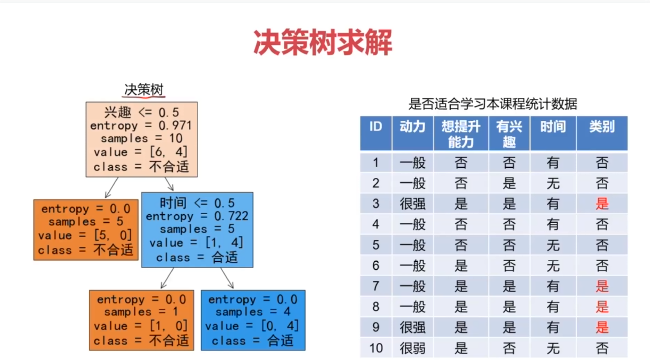
决策树:一种对实例进行分类的树形结构,通过多层判断区分目标所属类别
本质:通过多层判断,从训练数据集中归纳出一组分类规则
优点:
- 计算量小,运算速度快
- 易于理解,可清晰查看各属性的重要性
缺点:
- 忽略属性间的相关性
- 样本类别分布不均匀时,容易影响模型表现


参考资料:https://www.cnblogs.com/callyblog/p/9724823.html

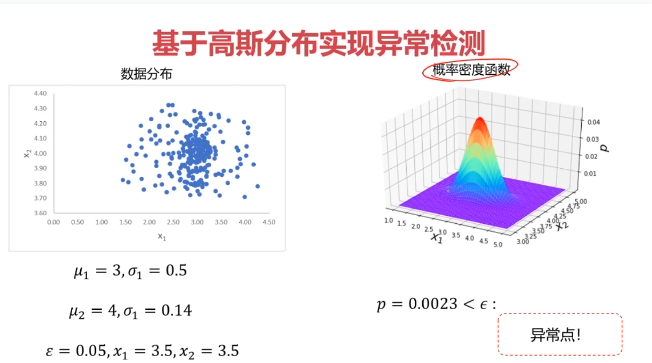
二、异常检测(Anomaly Detection)
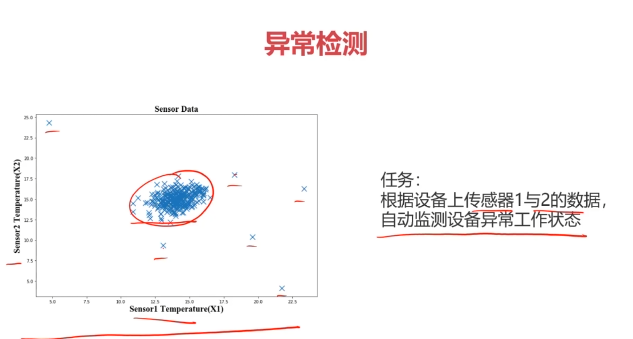
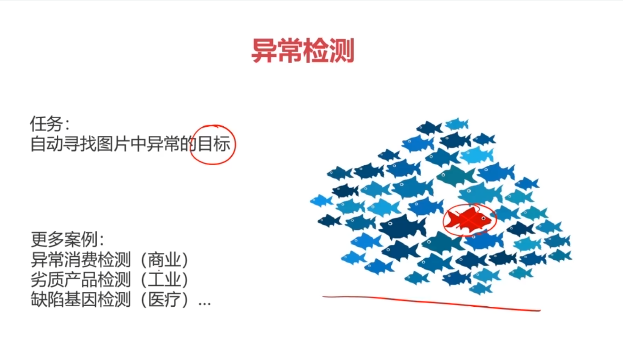
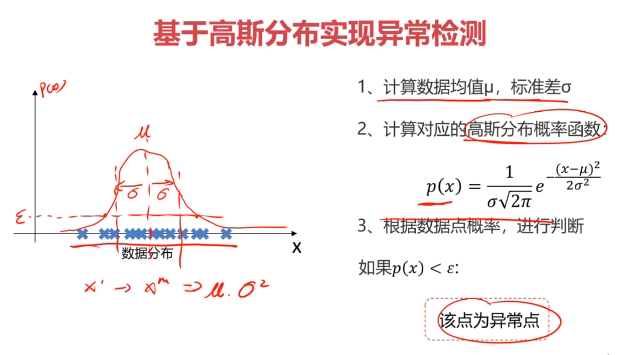
异常检测:根据输入数据,对不符合预期模式的数据进行识别
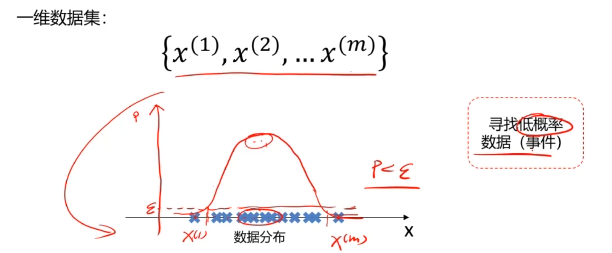
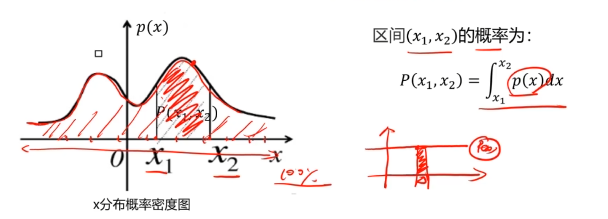
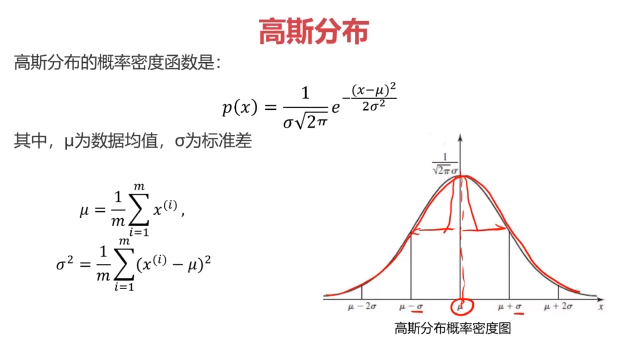
概率密度:概率密度函数是一个描述随机变量在某个确定取值点附近的可能性的函数
三、主成分分析(PCA)
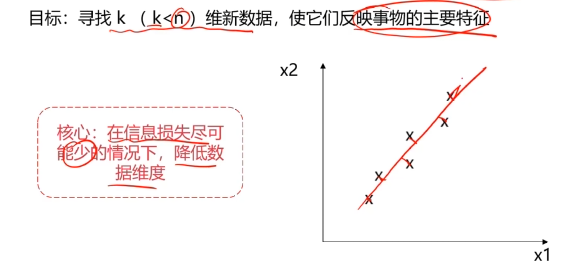
数据降维(Dimensionality Reduction)
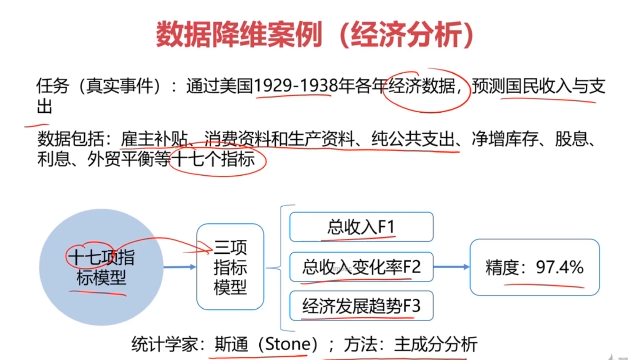
数据降维,是指在某些限定条件下,降低随机变量个数,得到一组“不相关”主变量的过程。
作用:
- 减少模型分析数据量,提升处理效率,降低计算难度;
- 实现数据可视化。
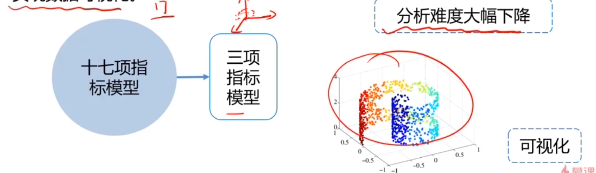
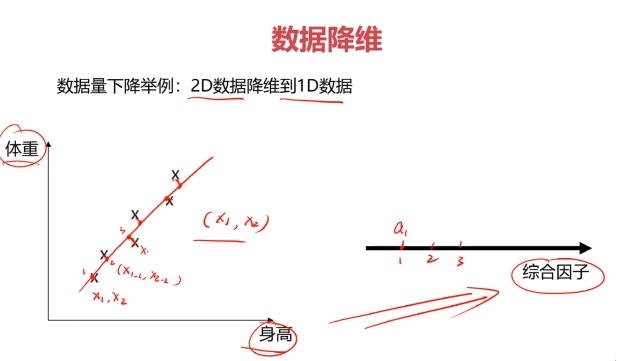
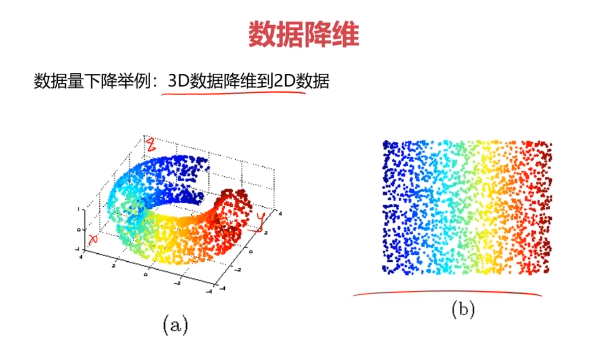
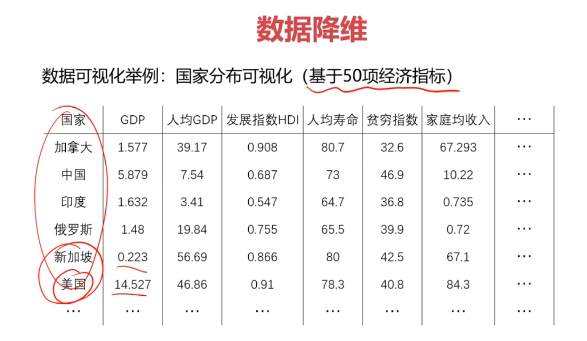
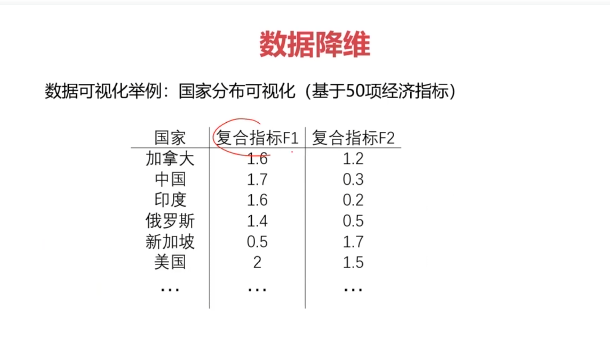
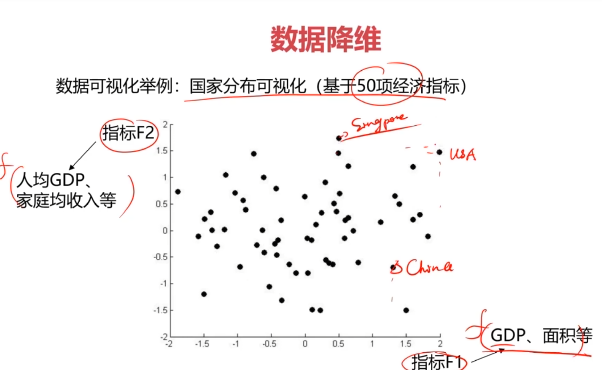
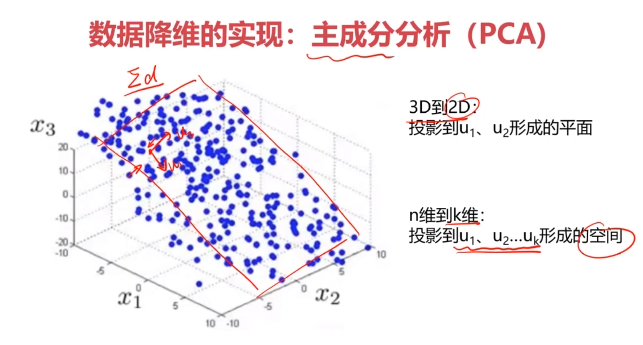
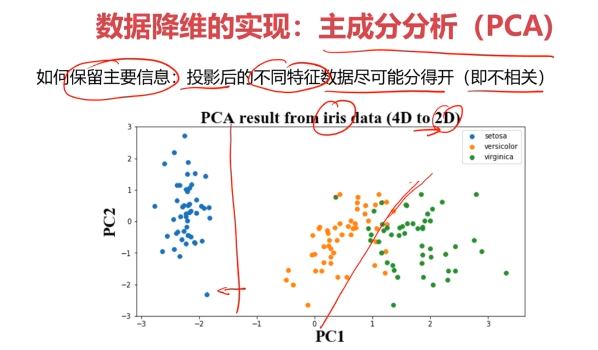
数据降维的实现:主成分分析(PCA)
PCA(principal components analysis):数据降维技术中,应用最最多的方法

四、Python实战准备

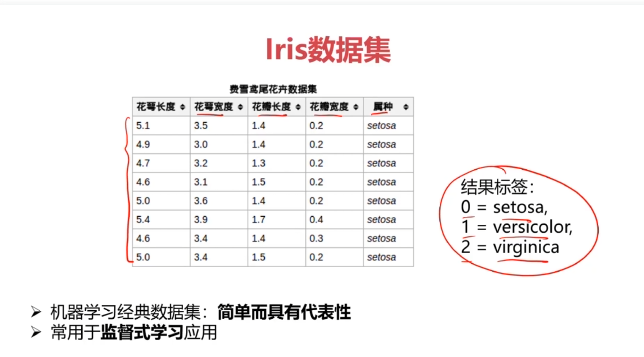
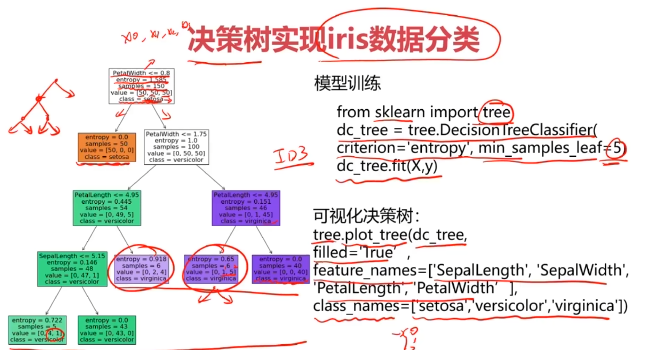
五、实战:决策树实现iris数据分类
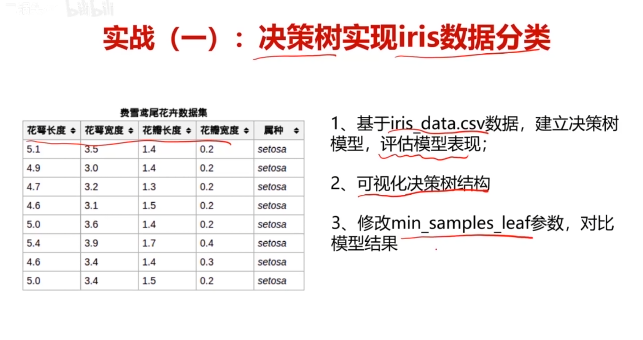
五、决策树实战,使用数据集iris_data.csv
#加载数据
import pandas as pd
import numpy as np
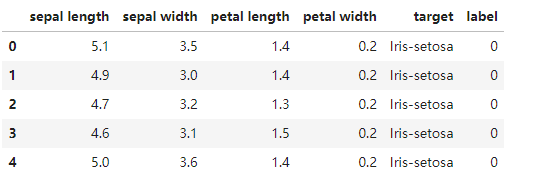
data = pd.read_csv('iris_data.csv')
data.head()
#赋值x,y
x = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']
print(x.shape,y.shape)

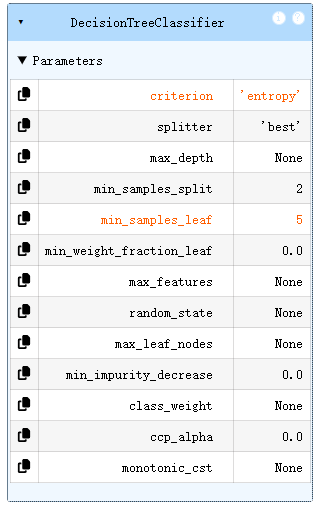
#创建决策树模型
from sklearn import tree
dc_tree = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=5)
dc_tree.fit(x,y)
#评估模型表现
y_predict = dc_tree.predict(x)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)
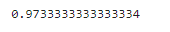
#可视化模型结构
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))
tree.plot_tree(dc_tree,filled=True,feature_names=['SepalLength','SepalWidth','PetalLength','PetalWidth'],class_names=['setosa','versicolor','virginica'])
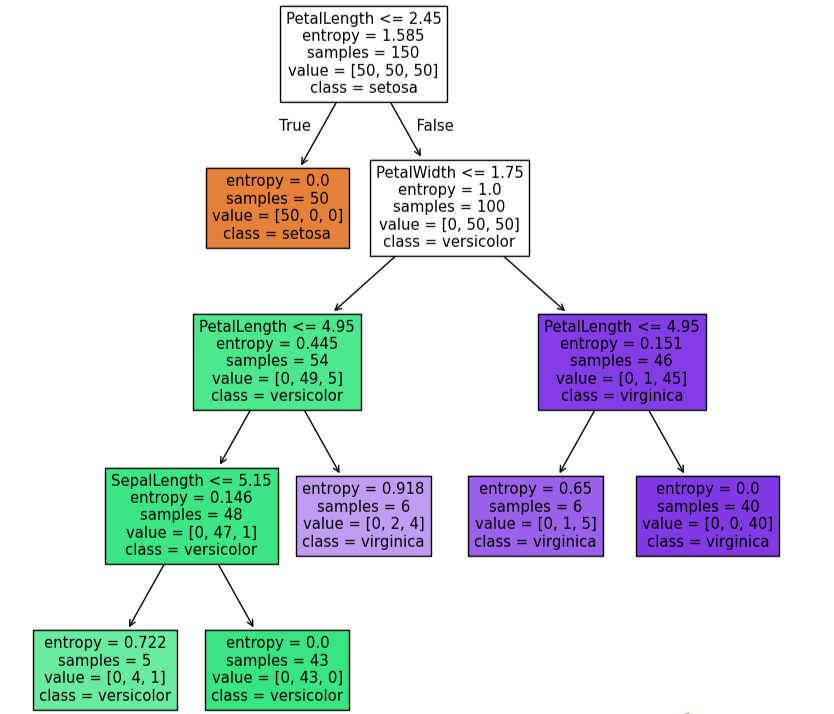
dc_tree = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=2)
dc_tree.fit(x,y)
fig = plt.figure(figsize=(10,10))
tree.plot_tree(dc_tree,filled=True,feature_names=['SepalLength','SepalWidth','PetalLength','PetalWidth'],class_names=['setosa','versicolor','virginica'])
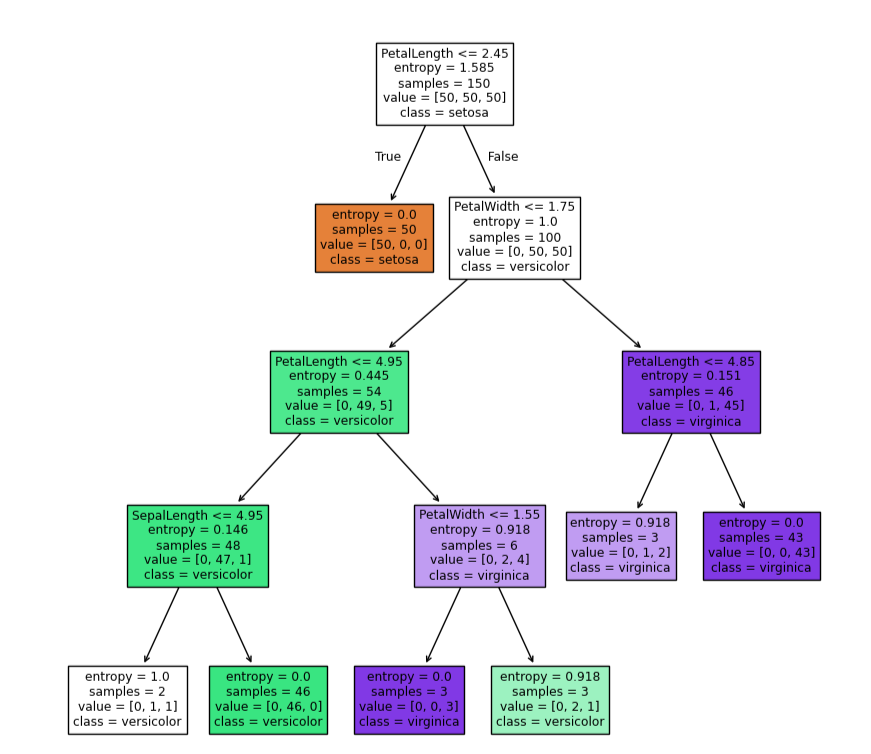
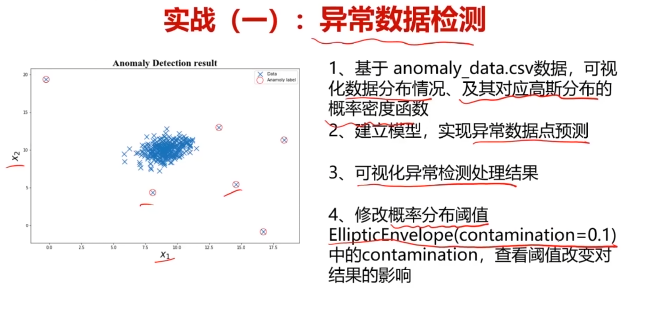
六、异常检测实战,使用数据集anomaly_data.csv
#异常检测
import pandas as pd
import numpy as np
data = pd.read_csv('anomaly_data.csv')
data.head()
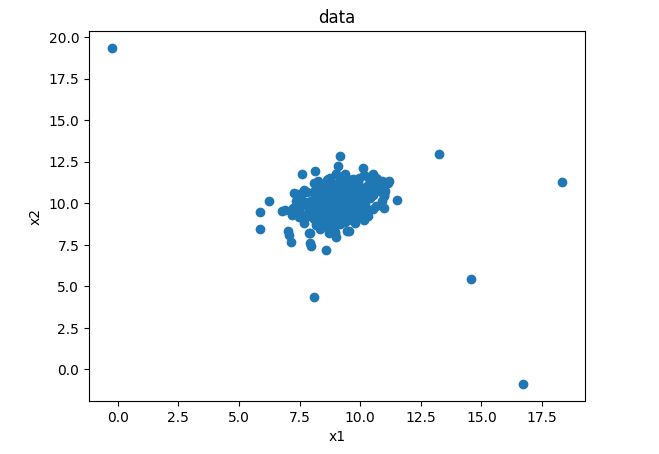
from matplotlib import pyplot as plt
fig3 = plt.figure()
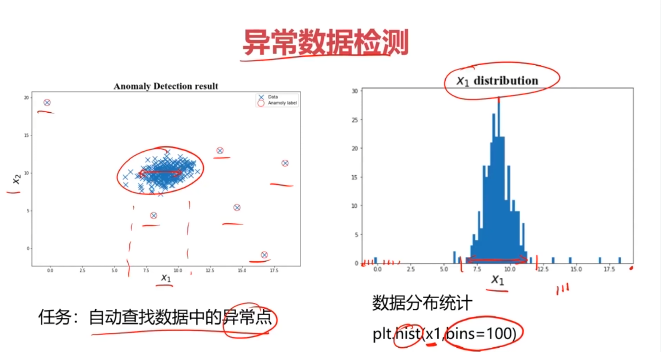
plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'])
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
#赋值x,y
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']
fig4 = plt.figure(figsize=(10,5))
plt.subplot(121)
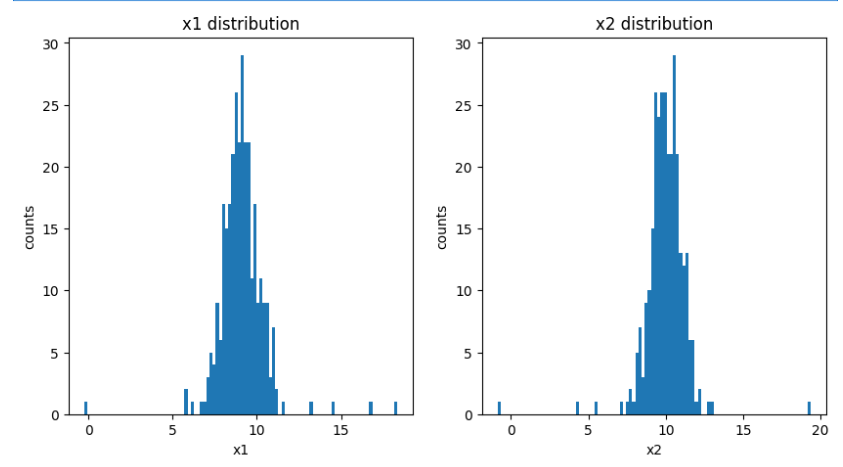
plt.hist(x1,bins=100)
plt.title('x1 distribution')
plt.xlabel('x1')
plt.ylabel('counts')plt.subplot(122)
plt.hist(x2,bins=100)
plt.title('x2 distribution')
plt.xlabel('x2')
plt.ylabel('counts')
plt.show()
#计算均值和标准差
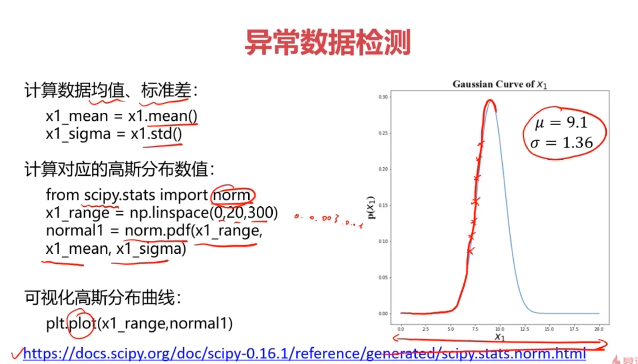
x1_mean = x1.mean()#均值
x1_signa = x1.std()#标准差
x2_mean = x2.mean()#均值
x2_signa = x2.std()#标准差
print(x1_mean,x1_signa,x2_mean,x2_signa)

#计算高斯分布密度函数
from scipy.stats import norm
x1_range = np.linspace(0,20,300)
x1_normal = norm.pdf(x1_range,x1_mean,x1_signa)x2_range = np.linspace(0,20,300)
x2_normal = norm.pdf(x2_range,x2_mean,x2_signa)
fig5 = plt.figure()
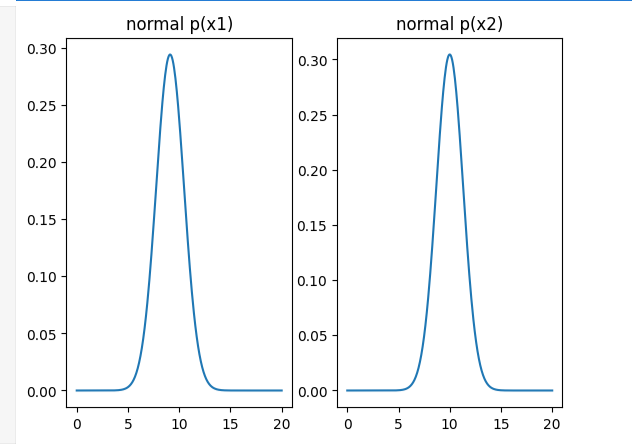
plt.subplot(121)
plt.plot(x1_range,x1_normal)
plt.title('normal p(x1)')plt.subplot(122)
plt.plot(x2_range,x2_normal)
plt.title('normal p(x2)')
plt.show()
#建立模型
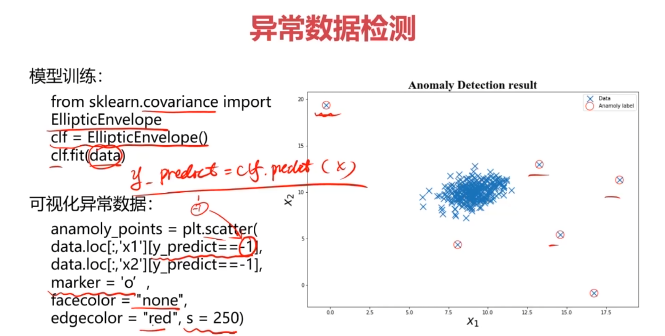
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope()
ad_model.fit(data)
#预测数据
y_predict = ad_model.predict(data)
print(y_predict)

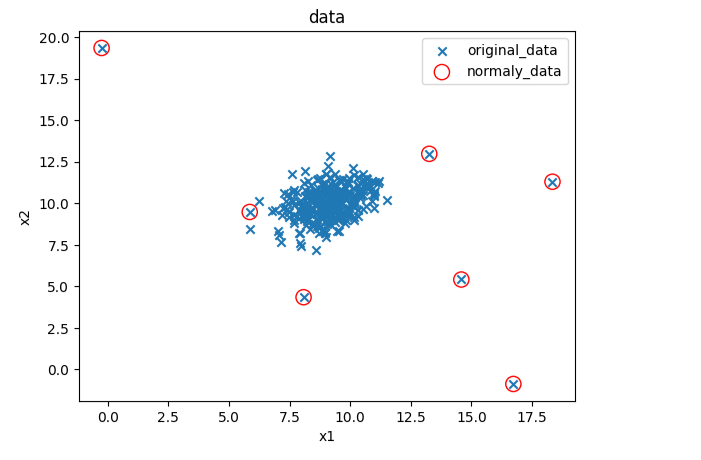
#可视化数据
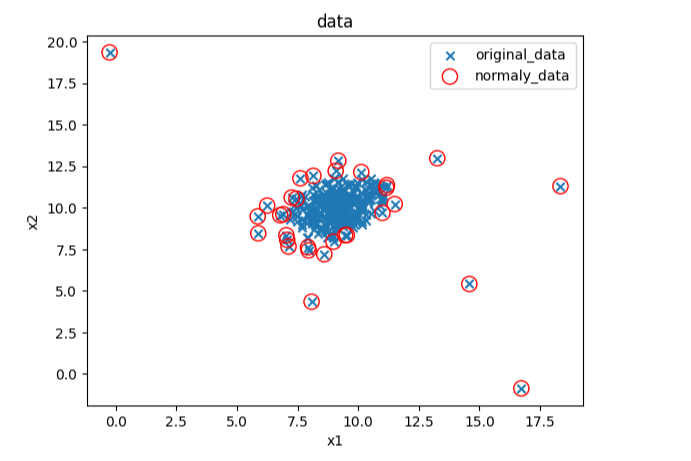
fig4 = plt.figure()
original_data=plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],marker='x')
normaly_data=plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1],marker='o',facecolor='none',edgecolor='red',s=120)
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((original_data,normaly_data),('original_data','normaly_data'))
plt.show()
#修改域值大小
ad_model = EllipticEnvelope(contamination=0.02)#默认0.1
ad_model.fit(data)
y_predict = ad_model.predict(data)#可视化数据
fig5 = plt.figure()
original_data=plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],marker='x')
normaly_data=plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1],marker='o',facecolor='none',edgecolor='red',s=120)
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((original_data,normaly_data),('original_data','normaly_data'))
plt.show()
七、主成分分析(PCA)实战,使用数据集iris_data.csv
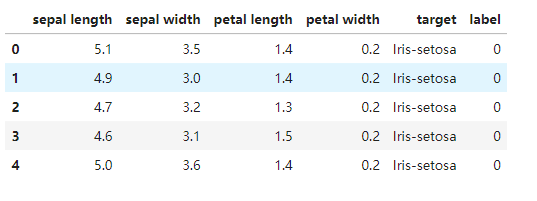
#加载数据
import pandas as pd
import numpy as np
data = pd.read_csv('iris_data.csv')
data.head()
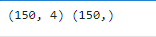
#赋值x,y
x = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']
print(x.shape,y.shape)
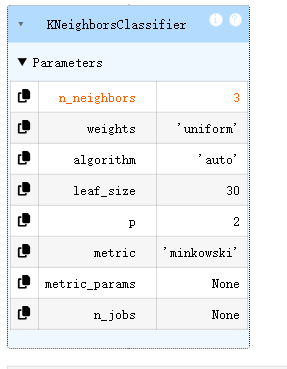
#KNN模型
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(x,y)
y_predict = KNN.predict(x)from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

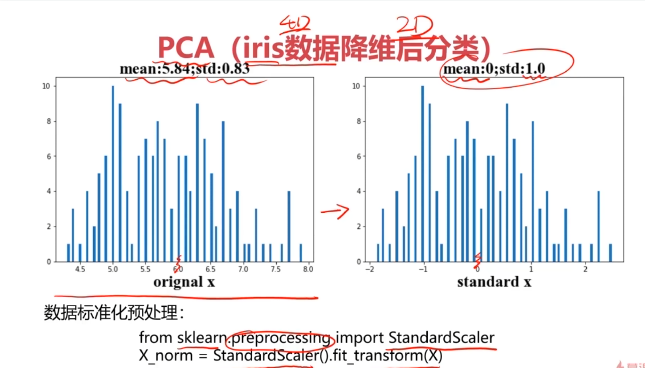
#数据预处理
from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(x)
print(X_norm)
#计算均值和标准差
x1_mean = x.loc[:,'sepal length'].mean()
x1_signa = x.loc[:,'sepal length'].std()X_norm_mean = X_norm[:,0].mean()
X_norm_signa = X_norm[:,0].std()print(x1_mean,x1_signa,X_norm_mean,X_norm_signa)

from matplotlib import pyplot as plt
fig1 = plt.figure()
plt.subplot(121)
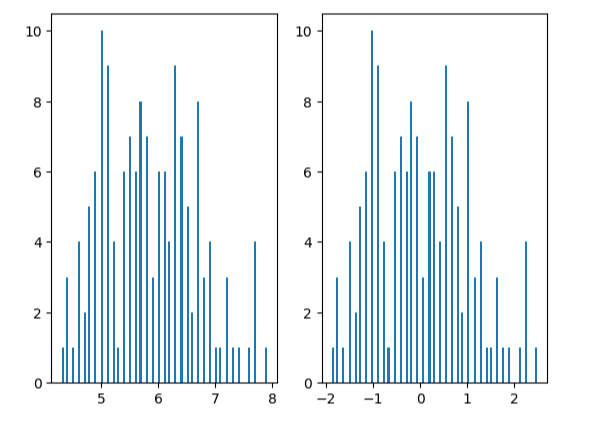
plt.hist(x.loc[:,'sepal length'],bins=100)plt.subplot(122)
plt.hist(X_norm[:,0],bins=100)
plt.show()
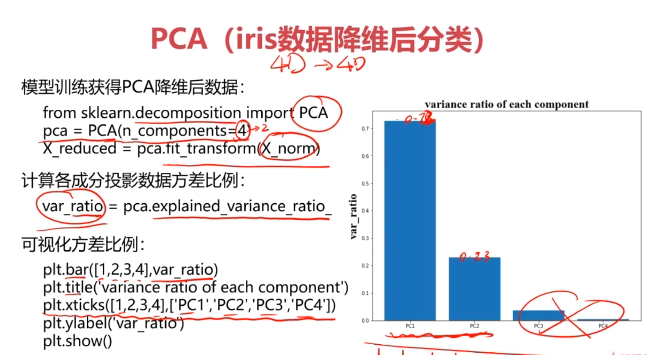
#主成分分析(PCA)
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
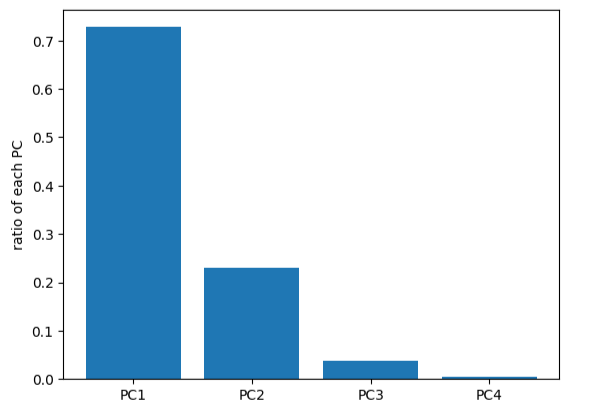
X_pca = pca.fit_transform(X_norm)#计算各个维度方差
var_ratio = pca.explained_variance_ratio_
print(var_ratio)

fig2 = plt.figure()
plt.bar([1,2,3,4],var_ratio)
plt.xticks([1,2,3,4],['PC1','PC2','PC3','PC4'])
plt.ylabel('ratio of each PC')
plt.show()
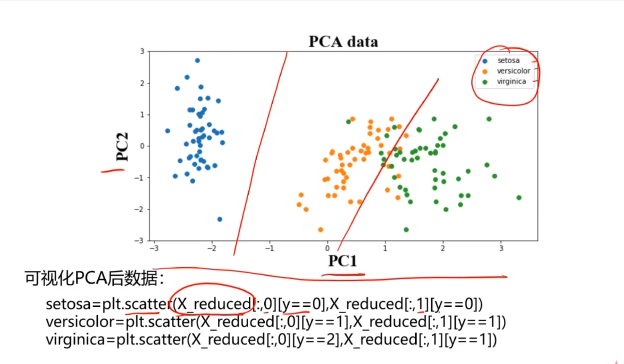
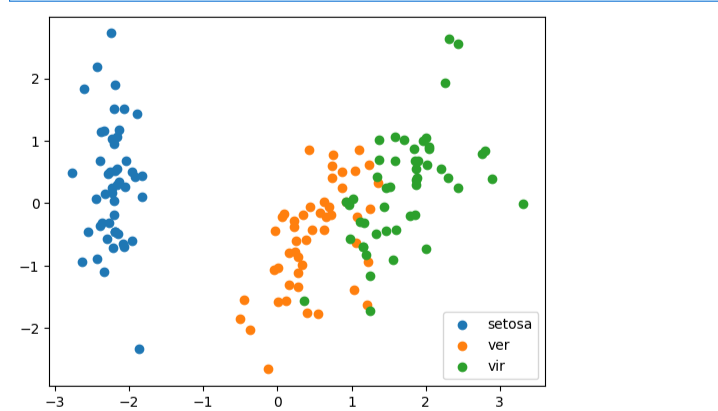
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_norm)
print(X_pca.shape,type(X_pca))

#可视化展示数据
fig3 = plt.figure()
setosa=plt.scatter(X_pca[:,0][y==0],X_pca[:,1][y==0])
ver=plt.scatter(X_pca[:,0][y==1],X_pca[:,1][y==1])
vir=plt.scatter(X_pca[:,0][y==2],X_pca[:,1][y==2])
plt.legend([setosa,ver,vir],['setosa','ver','vir'])
plt.show()
#创建降维后的KNN模型
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca,y)y_predict = KNN.predict(X_pca)from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)