当前位置：首页 > news >正文

LeetCode算法日记 - Day 36: 基本计算器II、字符串解码

news 2025/9/9 11:49:22

1. 基本计器II

1.1 题目解析

1.2 解法

1.3 代码实现

2. 字符串解码

2.1 题目解析

2.2 解法

2.3 代码实现

1. 基本计器II

227. 基本计算器 II - 力扣（LeetCode）

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

整数除法仅保留整数部分。

你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。

注意：不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "3+2*2"
输出：7

示例 2：

输入：s = " 3/2 "
输出：1

示例 3：

输入：s = " 3+5 / 2 "
输出：5

提示：

1 <= s.length <= 3 * 105
s 由整数和算符 ('+', '-', '*', '/') 组成，中间由一些空格隔开
s 表示一个 有效表达式
表达式中的所有整数都是非负整数，且在范围 [0, 231 - 1] 内
题目数据保证答案是一个 32-bit 整数

1.1 题目解析

题目本质：
这是一个只含 + - * / 和空格的中缀表达式求值问题，所有数为非负整数，/ 为向 0 取整。由于只有四则运算且 * / 优先于 + - ，可以在一次线性扫描中即时处理乘除、延后相加减。

常规解法：
最直观是“表达式转后缀 + 用栈求值”（或写一个带优先级的算符栈 + 数栈的通用计算器）。但这对本题有些“重炮打蚊子”。

问题分析：
通用双栈法实现复杂，且多做了括号/优先级的通用处理。本题没有括号，只需处理 * / 优先级即可。目标是在线性遍历里把每段“数字 + 运算符”的效果落到结果中，避免二次遍历或复杂结构。时间期望 O(n)。

思路转折：
要想高效 → 在扫描时遇到一个完整数字后，依据“上一个运算符”做处理：

若上一个是 +：把正数压栈；
- ：把负数压栈；
* /：从栈顶弹出一个数与当前数计算，再把结果压回栈；
这样就把 * / 的优先级即时消化了，最后把栈元素求和即答案。
实现要点：跳过空格；读多位数；到达末尾也要结算；只在是四个运算符时更新 op。

1.2 解法

算法思想：
线性扫描字符串，维护：

op：上一个运算符（初始为 '+'，便于处理开头的第一个数）；
一个整型栈 stack 存放尚未合并的“分项”（正负号已折算；乘除已即时合并）。
对每个读出的“完整数字 num”，按 op 执行：

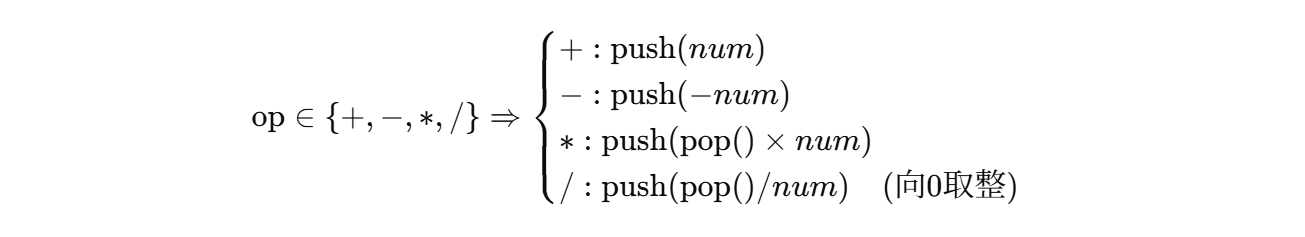
扫描结束后把栈中数累加。

i）把字符串转为 char[]，设 op='+'；

ii）外层 for 扫描下标 i：

若空格：跳过；
若是数字：从 i 开始继续读多位数字得到 num；
- 按 op 与 num 更新栈；
- 将 i 跳到数字末尾（外层 for 再自增一次）；
若是 + - * /：更新 op；

iii）循环结束，累加栈中所有数得到结果。

易错点：

读数越界：读多位数字时要先判 isTrue < n 再访问 ch[isTrue]。
末尾是数字：虽然末尾没有运算符，但读数的分支里已完成结算，不需要特殊额外处理；若用“遇符号或到末尾才结算”的写法，记得 || i == n-1。
空格当运算符：op 只在 + - * / 时更新，空格必须跳过。
除法语义：Java 整数相除默认向 0 取整，符合题意；注意负数除法同样向 0 取整。
首个数字：op 初始为 '+'，使首个数字按“加法”处理，避免特殊分支。

1.3 代码实现

import java.util.Stack;class Solution {public int calculate(String s) {Stack<Integer> stack = new Stack<>();int n = s.length();char[] ch = s.toCharArray();char op = '+'; // 上一个运算符，默认'+'for (int i = 0; i < n; i++) {if (ch[i] == ' ') continue; // 跳过空格if (Character.isDigit(ch[i])) {// 读多位数字：区间 [i, j)int j = i, num = 0;while (j < n && Character.isDigit(ch[j])) {num = num * 10 + (ch[j] - '0');j++;}// 按上一个运算符把 num 落到栈里if (op == '+') {stack.push(num);} else if (op == '-') {stack.push(-num);} else if (op == '*') {stack.push(stack.pop() * num);} else if (op == '/') {stack.push(stack.pop() / num); // 向0取整}i = j - 1; // 跳到数字末尾，外层for会再+1} else if (ch[i] == '+' || ch[i] == '-' || ch[i] == '*' || ch[i] == '/') {op = ch[i]; // 只有四则符号时才更新}// 其他字符（理论上不会出现）忽略}int res = 0;while (!stack.isEmpty()) res += stack.pop();return res;}
}

复杂度分析：

时间复杂度：O(n)，每个字符最多进出一次。
空间复杂度：O(n)（最坏全是加减时，栈里会存放 O(n) 个分项）。

2. 字符串解码

394. 字符串解码 - 力扣（LeetCode）

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

测试用例保证输出的长度不会超过 105。

示例 1：

输入：s = "3[a]2[bc]"
输出："aaabcbc"

示例 2：

输入：s = "3[a2[c]]"
输出："accaccacc"

示例 3：

输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

示例 4：

输入：s = "abc3[cd]xyz"
输出："abccdcdcdxyz"

2.1 题目解析

题目本质：
把形如 k[encoded_string] 的编码串解码为原串，k 可为多位数，encoded_string 允许嵌套。这是一个括号展开 + 嵌套上下文的问题。

常规解法：
直觉用递归：遇到 k[ 递归解析到匹配的 ]，返回子串并重复 k 次。

问题分析：
递归可行但要管理返回边界和深度；若用 String 拼接，容易退化成 O(n²)。而本题可以单次线性扫描完成，借助双栈把嵌套上下文管理清晰，并用 StringBuilder 保证线性拼接。

思路转折：
一次扫描，维护两栈：

intStack 存 每层的重复次数 k；
stringStack 存 每层进入前已构建的字符串段（最外层先压一个空 StringBuilder 作为根）。
遇数字累积；
遇 '[' 新开一层（把次数压入 intStack，把新空段压入 stringStack）
遇字母直接追加到当前层顶部段；
遇 ']' 弹出顶部段与次数，重复并追加回上一层顶部段。最终根层即答案。

2.2 解法

算法思想：

数字：累积多位 tmp = tmp*10 + (s[i]-'0') 后压入 intStack；
'['：从下一位开始把紧随的字母段收集成 tmp 段压入 stringStack（嵌套时后续会再遇到数字/[/字母分别处理）；
']'：弹出次数与段，把该段重复 k 次追加到上一层顶部段；
其它（字母）：把连续字母段追加到当前层顶部段。

i）char[] s = ss.toCharArray(); int n = s.length;

ii）栈初始化：stringStack.push(new StringBuilder()) 作为最外层；intStack 为空。

iii）while (i < n) 分支处理：数字段、'['、']'、普通字母段。

iiii）返回栈顶 toString()。

易错点：

多位数必须逐位累加：(s[i]-'0')。
'[' 后收集字母段要注意 i 的推进（每次追加都 i++）。
']' 时先弹字符串段，再弹次数，把重复后的结果追加到上一层的 peek。
根层占位必须先压一个空 StringBuilder，确保 peek() 永远存在。
判断字母/数字要用 s[i]，避免拿 i 与字符比较。

2.3 代码实现

import java.util.Stack;class Solution {public String decodeString(String ss) {char[] s = ss.toCharArray();int n = s.length;Stack<StringBuilder> stringStack = new Stack<>();stringStack.push(new StringBuilder()); // 根层：收集最外层结果Stack<Integer> intStack = new Stack<>();int i = 0;while (i < n) {if (s[i] >= '0' && s[i] <= '9') {// 读多位数字，压入次数栈int tmp = 0;while (i < n && s[i] >= '0' && s[i] <= '9') {tmp = tmp * 10 + (s[i] - '0');i++;}intStack.push(tmp);} else if (s[i] == '[') {// '[' 后面紧跟的连续字母，作为“新层的起始段”压入字符串栈i++;StringBuilder tmp = new StringBuilder();while (i < n && s[i] >= 'a' && s[i] <= 'z') {tmp.append(s[i]);i++;}stringStack.push(tmp);} else if (s[i] == ']') {// 弹出次数与段，把段重复并追加到上一层int tmpInt = intStack.pop();StringBuilder tmp = stringStack.pop();      // 当前层段StringBuilder top = stringStack.peek();     // 上一层段while (tmpInt > 0) {top.append(tmp);tmpInt--;}i++;} else {// 普通字母：收集连续字母并追加到当前层StringBuilder tmp = new StringBuilder();while (i < n && s[i] >= 'a' && s[i] <= 'z') {tmp.append(s[i]);i++;}stringStack.peek().append(tmp);}}return stringStack.pop().toString();}
}

复杂度分析（时间+空间）：