CD76.【C++ Dev】AVL的模拟实现(1) 以左单旋为切口,分析旋转规律
目录
1.知识回顾
2.节点类
3.insert函数(限于篇幅,只分析左单旋)
插入节点
更新平衡因子
从1变0
从0变1
平衡因子的向上调整算法
从-1变-2和从1变2(AVL树失衡,需要调整)
★★以左单旋为例,深度剖析调整规律(全文重点)★★
先向上调整
更新平衡因子+向上找到平衡因子越界的节点的代码
平衡因子为2,已经越界,停止向上调整值,需要调整AVL树,进行左单旋
从模块的角度讨论左单旋
前置知识:判断二叉搜索树的节点的大小关系
从简单的情况逐步演变,推出规律
旋转的提示
RotateLeft函数编写
★总结平衡因子更新策略
4.二叉树可视化在线网站
1.知识回顾
之前在C++ Contest专栏讲过AVL树:
CC40.【C++ Cont】二叉搜索树和平衡二叉树
本文深入讲解模拟实现
2.节点类
使用三叉链的写法,存3个指针
template<class K,class V>
class AVLTreeNode
{
public:AVLTreeNode(const std::pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_pack(kv),_bf(0){ }AVLTreeNode<K,V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int8_t _bf;std::pair<K, V> _pack;
};注:1.三叉链:比一般的二叉树的节点类要多用一个指针指向父节点,这样就方便向上找根节点
2._bf是Balance Factor平衡因子的缩写,一开始插入这个节点的平衡因子为0,因为这个节点没有左子树或右子树
3.insert函数(限于篇幅,只分析左单旋)
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://......
private:Node* _root;
};插入节点
一开始是个空树,直接修改_root为插入的节点
Node* node = new Node(kv);
if (_root == nullptr)
{_root = node;return true;
}然后借用之前的二叉搜索树的代码:
while (cur)
{if (cur->_pack.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_pack.first > kv.first){parent = cur;cur = cur->_left;}else//cur->_pack.first == kv.first{return false;}
}利用parent指向的节点存储的的左右指针来确定node的位置:
如果parent->_pack.first > kv.first,那么:

如果parent->_pack.first < kv.first,那么:
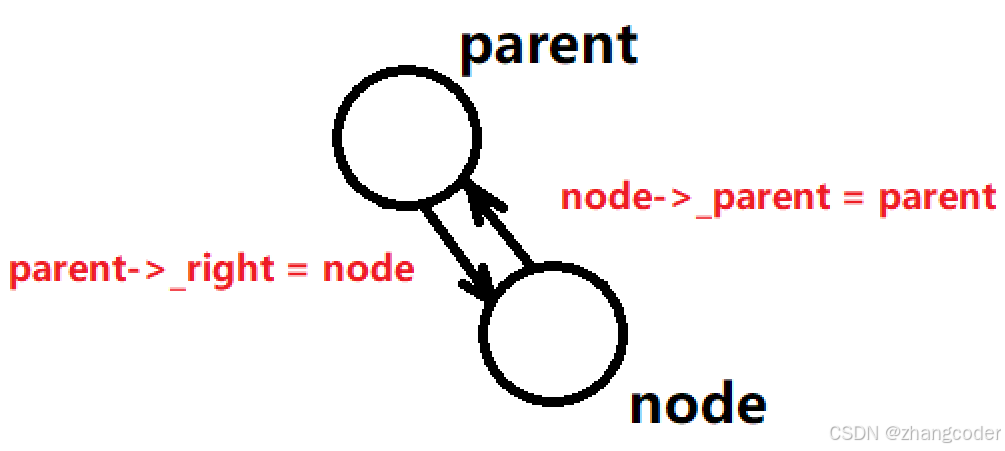
//找到了需要修改指针的节点,设置指针
if (parent->_pack.first < kv.first)parent->_right = node;
else//parent->_pack.first > kv.firstparent->_left = node;
cur = node;
node->_parent = parent;更新平衡因子
设平衡因子的大小==右子树的高度-左子树的高度
枚举平衡因子大小变化的情况:
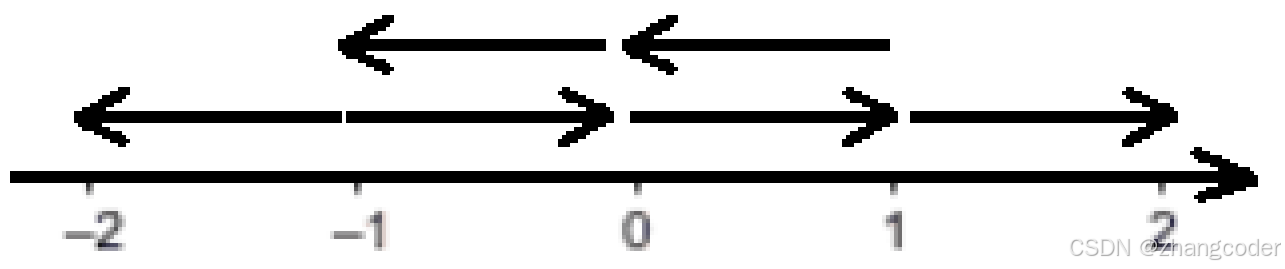
注: 一般情况下,平衡因子不可能绝对值为3,但程序可能出bug,建议代码中额外判断一下
更新平衡因子后,某些情况下插入节点会导致AVL树不平衡,那么判断AVL树是否平衡需要看平衡因子
平衡因子的值在[-1,1]之间变化是正常的,如果从-1到-2或者-2到-1,需要将不平衡的树调整为AVL树
下面看6种变化情况的示意图:
下面分析这棵标注了平衡因子的AVL树
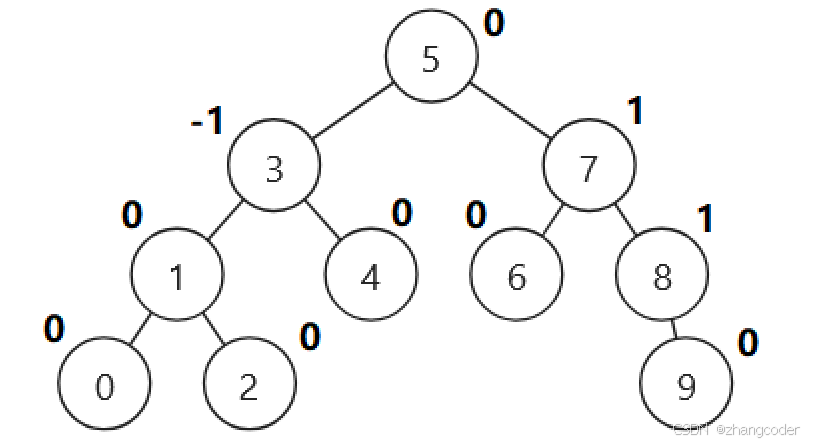
从1变0
树仍然是平衡的,不需要调整
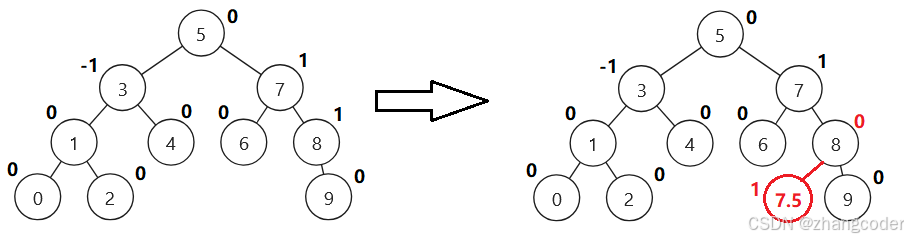
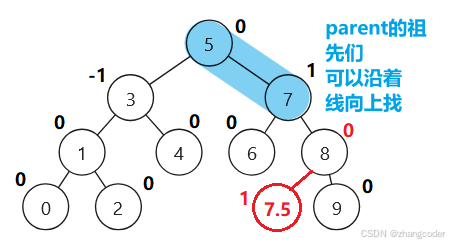
cur指向7.5,parent指向8,那么parent的平衡因子的变化为parent->_bf--,但parent的祖先节点们的平衡因子是不用调整的,因为平衡因子变成0说明以parent指向的根节点对应的树高度不变
平衡因子从0变成1或从0变成-1,树高度变
平衡因子从1变成0或从-1变成0,树高度不变
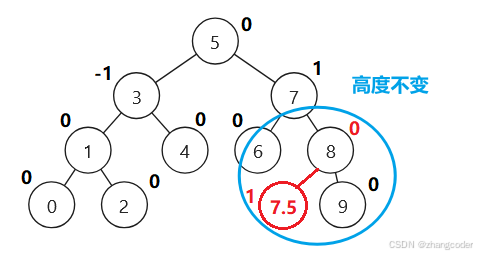
从0变1
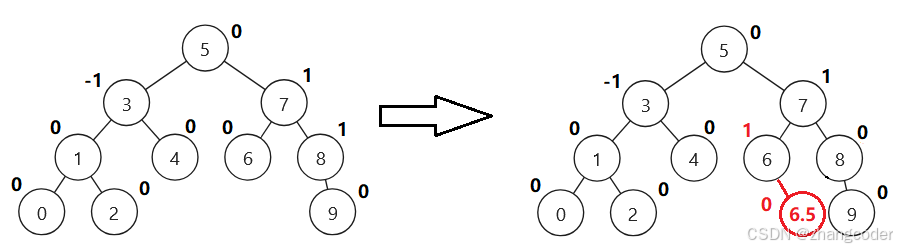
cur指向6.5,parent指向8,那么parent的平衡因子的变化为parent->_bf++,但parent的祖先节点们的平衡因子是需要向上调整的,因为平衡因子变成0说明以parent指向的根节点对应的树高度变了,会影响上面节点对应的树的高度
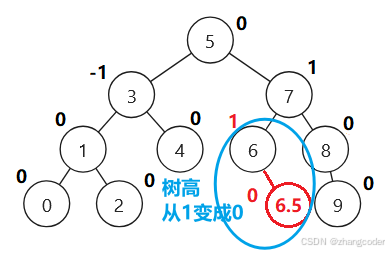
平衡因子的向上调整算法
需要向上调整上图parent指向节点的平衡因子和和的祖先节点们的平衡因子
向上调整即沿着祖先路径向上更新,而且向上更新有parent指针操作会很简单
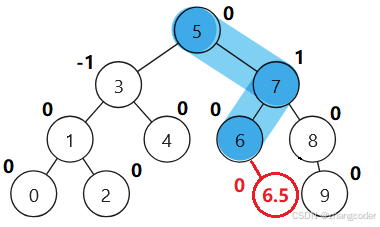
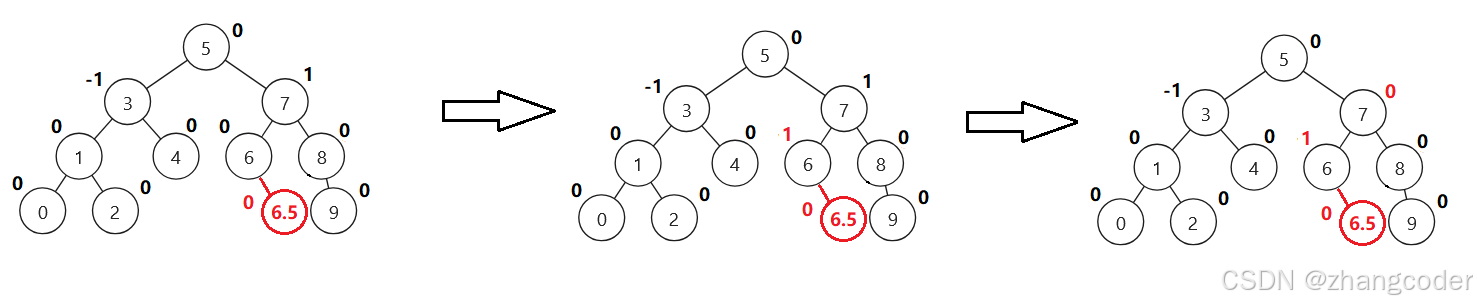
沿着祖先路径更新平衡因子,如果平衡因子更新为0,就不用向上继续更新,因为平衡因子变成0说明\根节点对应的树高度不变
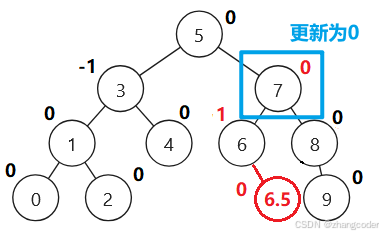
略去从-1变0和从0变-1,画法和平衡因子的向上调整算法同上,不再赘述
从-1变-2和从1变2(AVL树失衡,需要调整)
从-1变-2和从1变2都会时平衡因子越界,导致AVL树失衡,需要调整
★★以左单旋为例,深度剖析调整规律(全文重点)★★
将新节点插入到最小不平衡子树的根的右边,即CC40.【C++ Cont】二叉搜索树和平衡二叉树文章提到的RR型
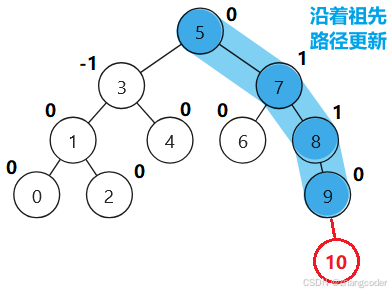
先向上调整
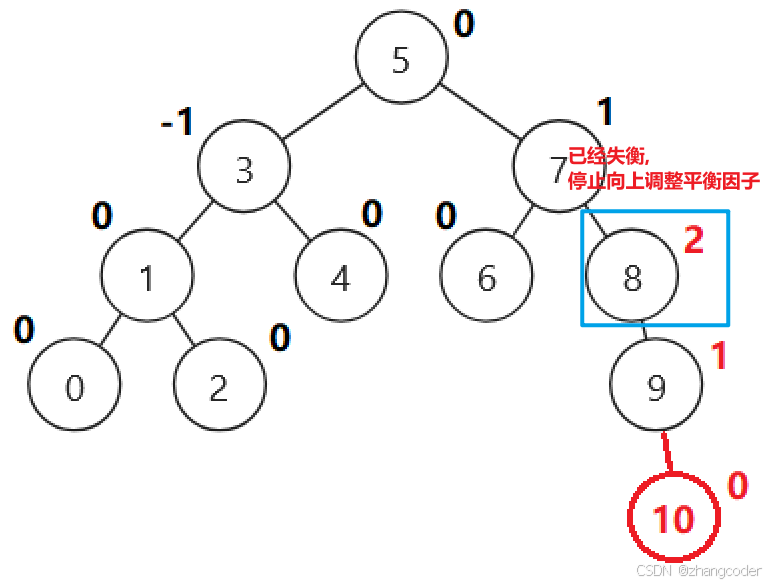
更新平衡因子+向上找到平衡因子越界的节点的代码
循环结束后,cur指向新插入的节点,parent指向新插入节点的父节点
//向上更新平衡因子
while (parent)
{if (parent->_left == cur)parent->_bf--;else//parent->_right == curparent->_bf++;if (parent->_bf == 0)break;else if (abs(parent->_bf) == 1){//继续向上更新cur = parent;parent = parent->_parent;}else if (abs(parent->_bf) == 2){//需要调整}else//防止出现异常情况{cout << "Balance Factor out of range!" << endl;assert(false);}
}平衡因子为2,已经越界,停止向上调整值,需要调整AVL树,进行左单旋
从模块的角度讨论左单旋
前置知识:判断二叉搜索树的节点的大小关系
对于以下的二叉搜索树,问a、b、c、d节点对应的值的大小关系
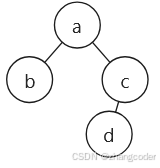
解:
显然b<a<c,d<c,那么d和a是什么大小关系?
要明确节点的插入顺序:a、b、c节点比d先插入,当d插入时要沿着二叉树去找可以存放的位置:
d插入到c的左子树,那么由二叉搜索树的性质可知一定有d>a
那么答案为: b<a<d<c
从简单的情况逐步演变,推出规律
旋转的提示
1.保持是搜索树
2.变成平衡树且降低子树的高度
★从最简单的情况看起,然后一步一步拓展★
▲注: 下面讨论的几种方法虽然能帮助考试快速写出正确代码,但是讨论不严谨,情况不全,之后会单独讲树插入的所有情况的枚举
情况A.最简单的情况
设c为新增节点:
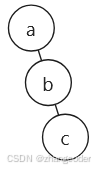
节点a的平衡因子为2,需要旋转,根据前置知识,节点的大小关系为a<b<c
根据a<b<c旋转为AVL树:"a<b<c"的b处于不等式的中间,所以b为根
那么有:
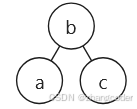
就有旋转这一说法了:右边高,往左边旋转; 左边高,往右边旋转
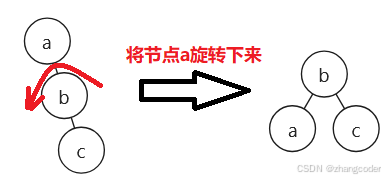
情况B.拓展最简单的情况,未旋转前,如果a上面有根,然后插入c
向上检测到a的平衡因子为2,需要旋转:
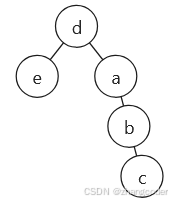
得出a、b、c都小于d,将a、b、c旋转后,d的right指针要设置为b:
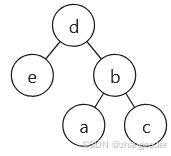
情况C.再拓展情况,未旋转前,如果a有左子树,然后插入c
向上检测到d的平衡因子为2,需要旋转:
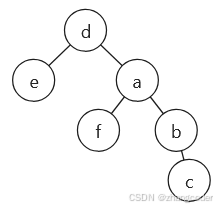
[1,1,1,null,null,1,1,null,null,null,null,null,null,1]
节点的大小关系为:e<d<a<b<c,且一定有f>d和f<a成立,那么:
e<d<f<a<b<c
由前置知识得出:
方法1: 如果f做根节点,那么就将临近的3个节点a<b<c排成完全二叉搜索树:
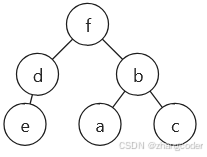
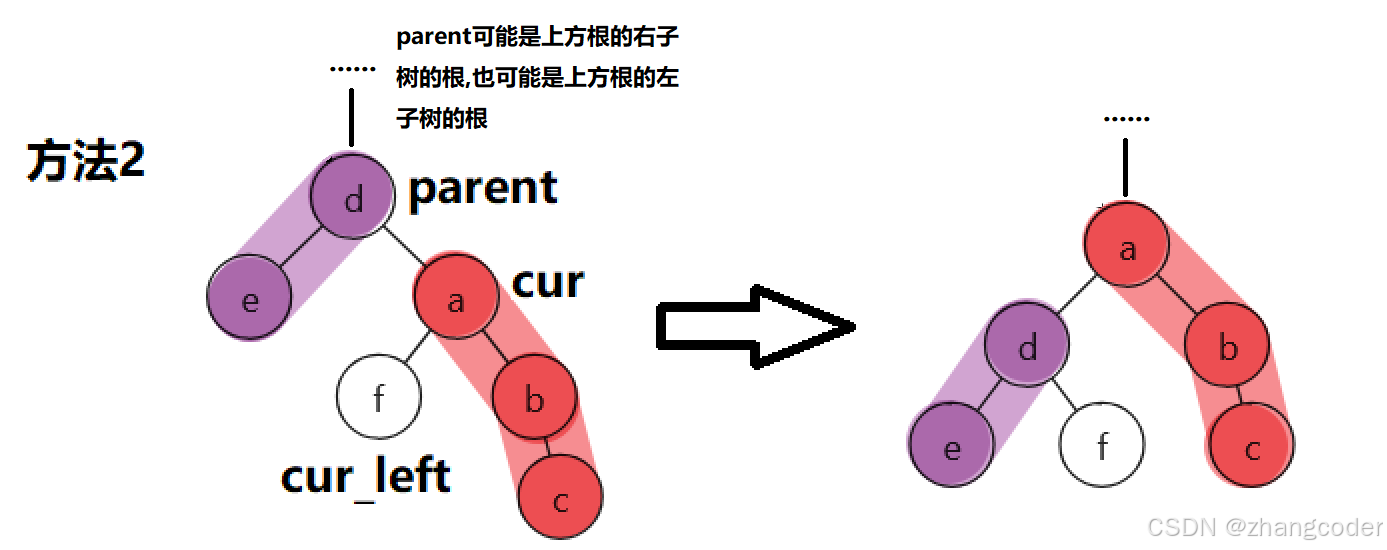
方法2: 如果a做根节点,那么就将临近的3个节点e<d<f排成完全二叉搜索树:
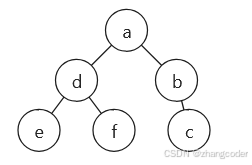
这两种做法都可以,但修改步骤最少的是方法2
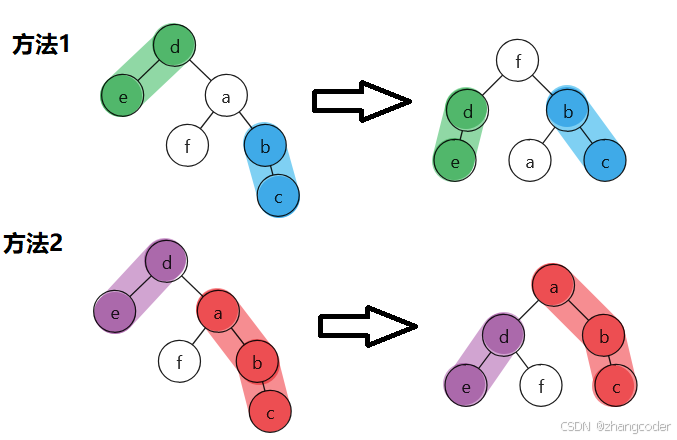
方法1:
//不考虑parent成员变量
f->left=d;
f->right=b;
a->left=nullptr;
a->right=nullptr;
d->right=nullptr;
b->left=nullptr;方法2:
//不考虑parent成员变量
a->left=d;
d->right=f;显然方法2步骤更少,效率更高!
情况D.再拓展情况,未旋转前,如果d上面有根且然后插入c
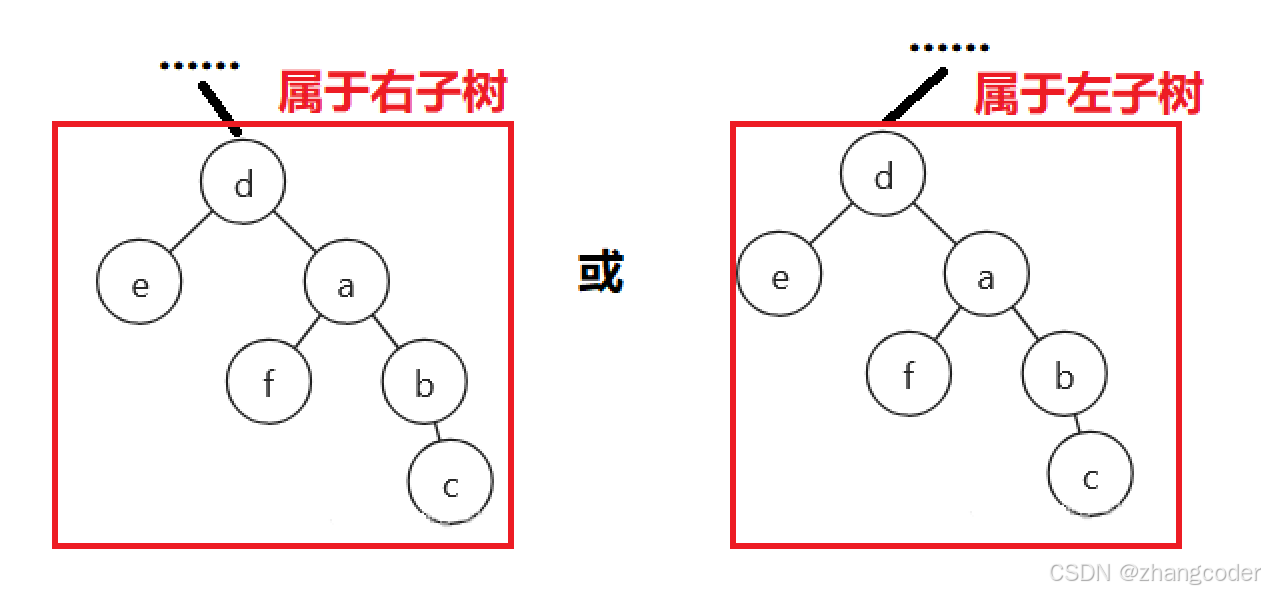
旋转上方和情况C一样,只需要设置上方的指针(......对应的节点的左指针和右指针)
左单旋(含设置平衡因子)之后,停止向上设置平衡因子,因为树已经平衡,且满足二叉搜索树的性质,插入函数结束
RotateLeft函数编写
注意既要考虑一般情况(上方的情况D),也要考虑特殊情况(上方的情况A、B和C),需要分类讨论
左旋的条件:从CC40.【C++ Cont】二叉搜索树和平衡二叉树文章得知,插在最小不平衡子树的根的右孩子的右子树上,如果从平衡因子来看,显然满足的条件为:
parent指向平衡因子为2的节点:
if (parent->_bf == 2 && cur->_bf == 1)
{RotateLeft(parent);break;//调整后就停止向上查找
}私有成员函数RotateLeft只需要改动这几个指针:
一般情况下(上方讲的情况D):
先定义3个指针:
void RotateLeft(Node* parent)
{Node* cur = parent->_right;Node* cur_left = cur->_left;Node* grandparent = parent->_parent;//parent的父节点//......
}
修改指针成员变量:需要修改3个节点的_parent指针:
cur->_parent = grandparent;
parent->_parent = cur;
cur_left->_parent = parent;再修改两个节点的_left和_right指针:
parent->_right = cur_left;
cur->_left = parent;还要设置grandparent的_left或_right指向新节点(不容易考虑到)
if (grandparent->_left == parent)
{grandparent->_left = cur;
}
else//grandparent->_right == parent
{grandparent->_right = cur;
}第一版代码:
void RotateLeft(Node* parent)
{Node* cur = parent->_right;Node* cur_left = cur->_left;Node* grandparent = parent->_parent;//parent的父节点cur->_parent = grandparent;parent->_parent = cur;cur_left->_parent = parent;parent->_right = cur_left;cur->_left = parent;if (grandparent->_left == parent){grandparent->_left = cur;}else//grandparent->_right == parent{grandparent->_right == cur;}
}情况D退化到情况C,需要修改第一版的代码
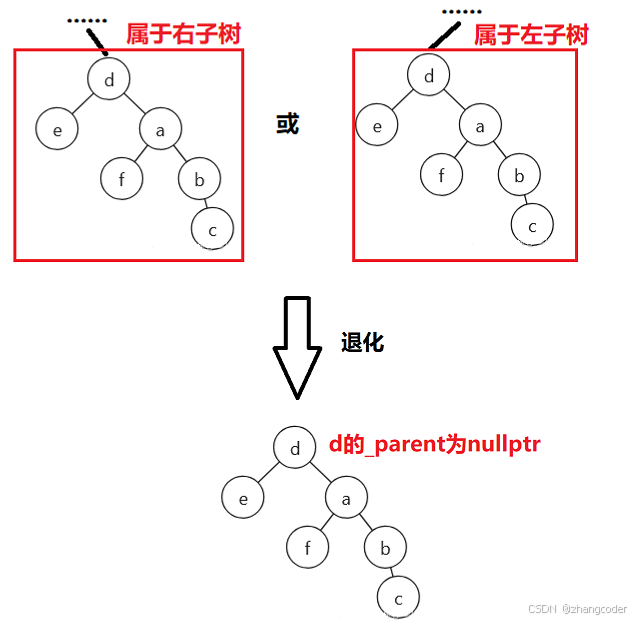
情况C有一个很明显的标志:parent == _root且grandparent == nullptr
需要对第一版代码添加判断条件,分出情况C和情况D
可以这样做:
if (parent == _root)
{//......
}
else
{//......
}第二版代码:
void RotateLeft(Node* parent)
{Node* cur = parent->_right;Node* cur_left = cur->_left;Node* grandparent = parent->_parent;//parent的父节点//如果是情况C,那么因为有构造函数,grandparent为nullptr,cur->_parent值是正确的cur->_parent = grandparent;parent->_parent = cur;cur_left->_parent = parent;parent->_right = cur_left;cur->_left = parent;if (parent == _root){_root = cur;}else//grandparent!=nullptr{if (grandparent->_left == parent){grandparent->_left = cur;}else//grandparent->_right == parent{grandparent->_right == cur;}}
}情况C退化到情况B,需要修改第二版的代码
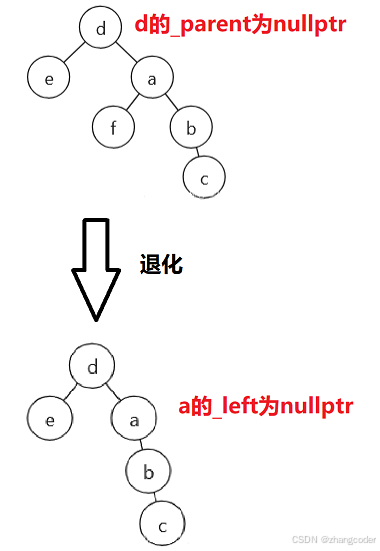
为了分出情况B和情况C,需要判断cur_left是否为空
那么执行cur_left->_parent = parent前需要添加判断,否则可能出现nullptr->_parent = parent错误
第三版代码
void RotateLeft(Node* parent)
{Node* cur = parent->_right;Node* cur_left = cur->_left;Node* grandparent = parent->_parent;//parent的父节点//如果是情况C,那么因为有构造函数,grandparent为nullptr,cur->_parent值是正确的cur->_parent = grandparent;parent->_parent = cur;if (cur_left){cur_left->_parent = parent;}parent->_right = cur_left;//如果cur_left为nullptr,那么parent->_rightt为nullptrcur->_left = parent;if (parent == _root){_root = cur;}else//grandparent!=nullptr{if (grandparent->_left == parent){grandparent->_left = cur;}else//grandparent->_right == parent{grandparent->_right == cur;}}
}情况B退化到情况A,但不需要修改第三版的代码
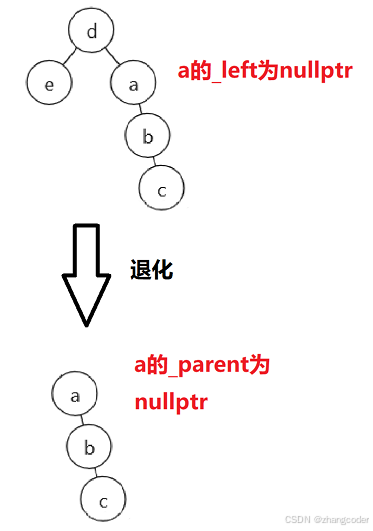
最后再设置平衡因子
注:下图的数字表示平衡因子,其大小定义为右子树的高度-左子树的高度
如果是情况A:
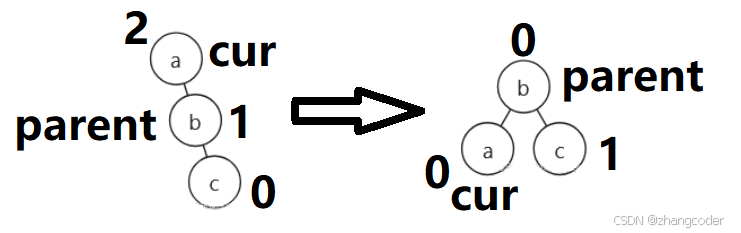
如果是情况B:
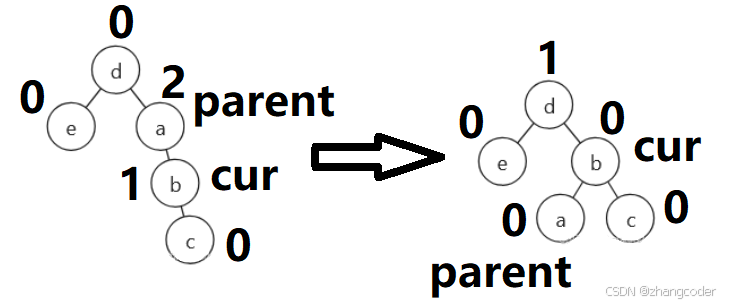
如果是情况C:
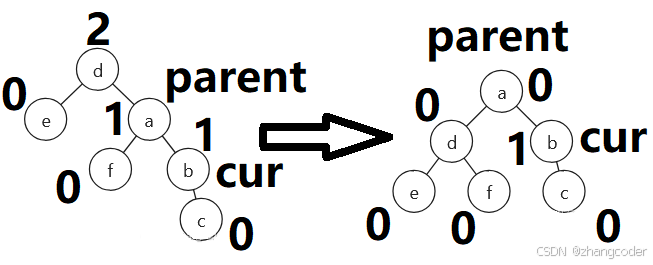
如果是情况D:
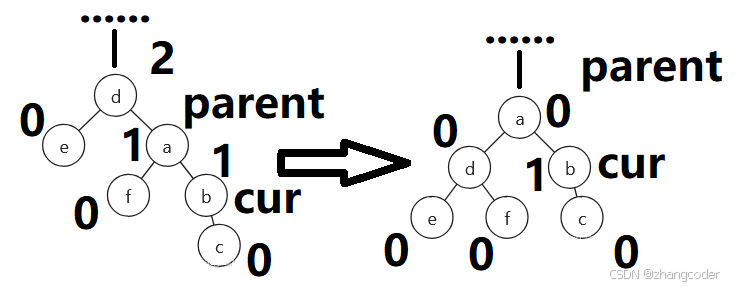
向上更新平衡因子时已经做过一部分平衡因子的调整内容,这里仅需要调整parent和cur的平衡因子
在RotateLeft的结尾写上:
parent->_bf = cur->_bf = 0;
结论:旋转只操作子树,而且会降低这个子树的高度
★总结平衡因子更新策略
平衡因子的作用: 检测树是否平衡
1. 新增在左,parent平衡因子--
2. 新增在右,parent平衡因子++
3. 更新后parent平衡因子==0,说明parent所在的子树的高度不变,不会再影响祖先,不用再继续沿着到root的路径往上更新,回到第1步继续调整,如果整棵树的根的平衡因子调整完了,插入函数结束
4. 更新后parent平衡因子==1或-1,说明parent所在的子树的高度变化,会再影响祖先,需要继续沿着到root的路径往上更新,回到第1步继续调整,如果整棵树的根的平衡因子调整完了,插入函数结束5. 更新后parent平衡因子==2或 -2,说明parent所在的子树的高度变化且不平衡,需要对parent所在子树进行旋转,让树平衡,插入函数结束
4.测试代码
测试含测试单关键字的AVL树:
#include "AVLTree.h"
using namespace std;
int main()
{AVLTree<int, nullptr_t> tree;//测试单关键字tree.insert(make_pair(1,nullptr));tree.insert(make_pair(2, nullptr));tree.insert(make_pair(3, nullptr));return 0;
}运行结果:
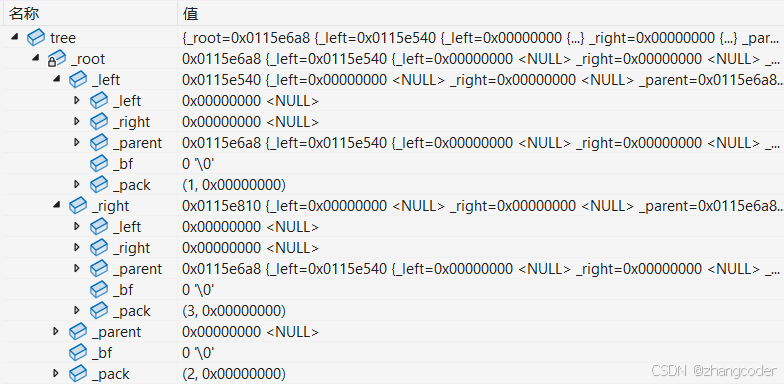
继续添加节点:
tree.insert(make_pair(4, nullptr));
tree.insert(make_pair(5, nullptr));运行结果:

继续添加节点:

测试的结果都没有问题
5.二叉树可视化在线网站
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html可动态展示AVL树的增删查改

