数据结构之二叉树(2)
数据结构之二叉树(2)
- 1.二叉树的存储结构
- 2.实现顺序结构二叉树
- 2.1何为堆
- 2.2堆的性质
- 2.3堆的定义
- 2.3堆的初始化与销毁
- 3.1向上调整算法
- 3.2向下调整算法
- 4.入堆
- 5.出堆
让花成花,让树成树
上一次我们学习了树的分类,并初步了解了二叉树。
今天我们深入了解二叉树并写出C语言代码
1.二叉树的存储结构
在学习C语言时,我们就知道了数据有两种存储结构,一种是顺序结构,一种是链式结构。
对于用数组来实现的二叉树,完全二叉树要优于非完全二叉树。
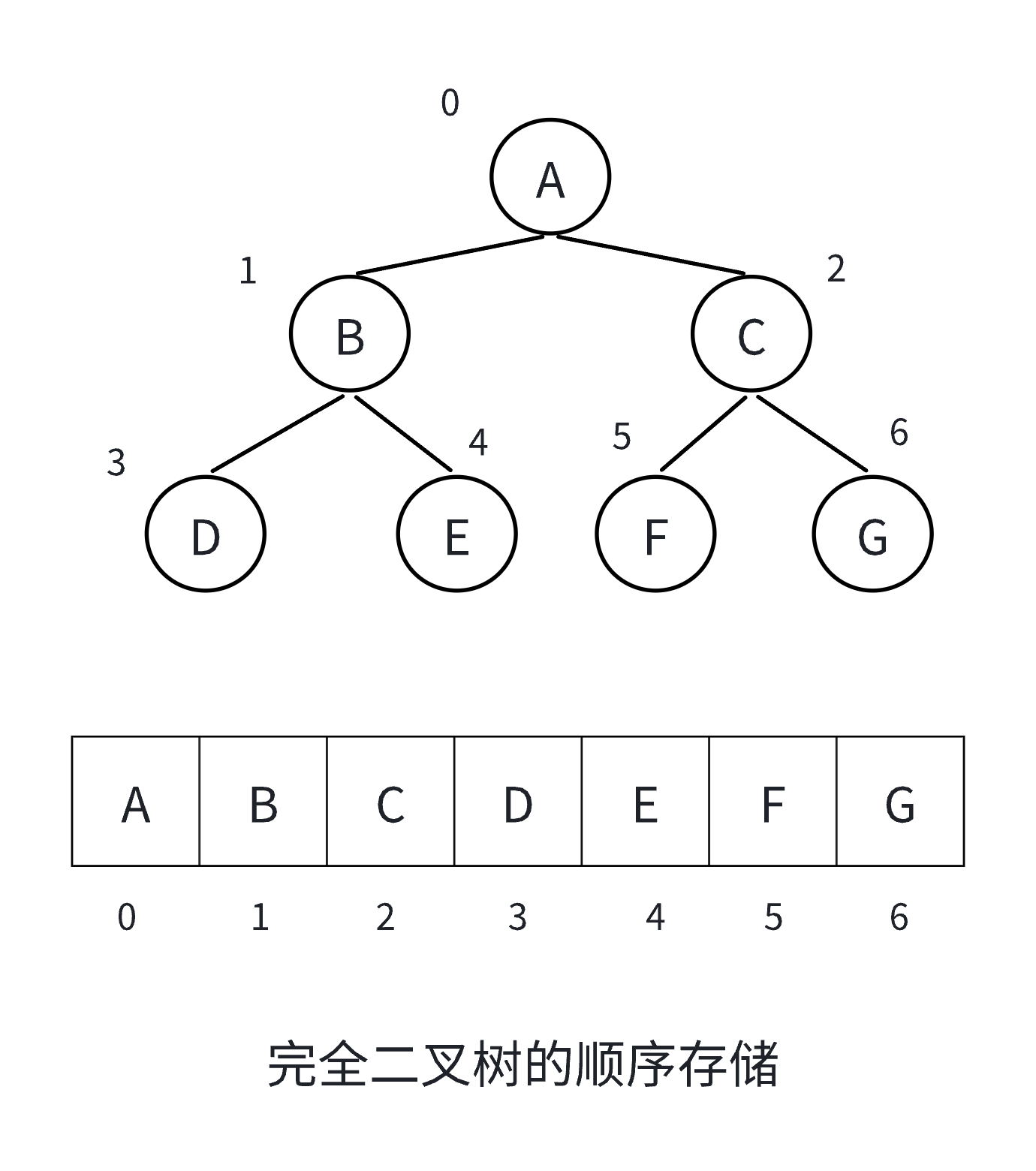
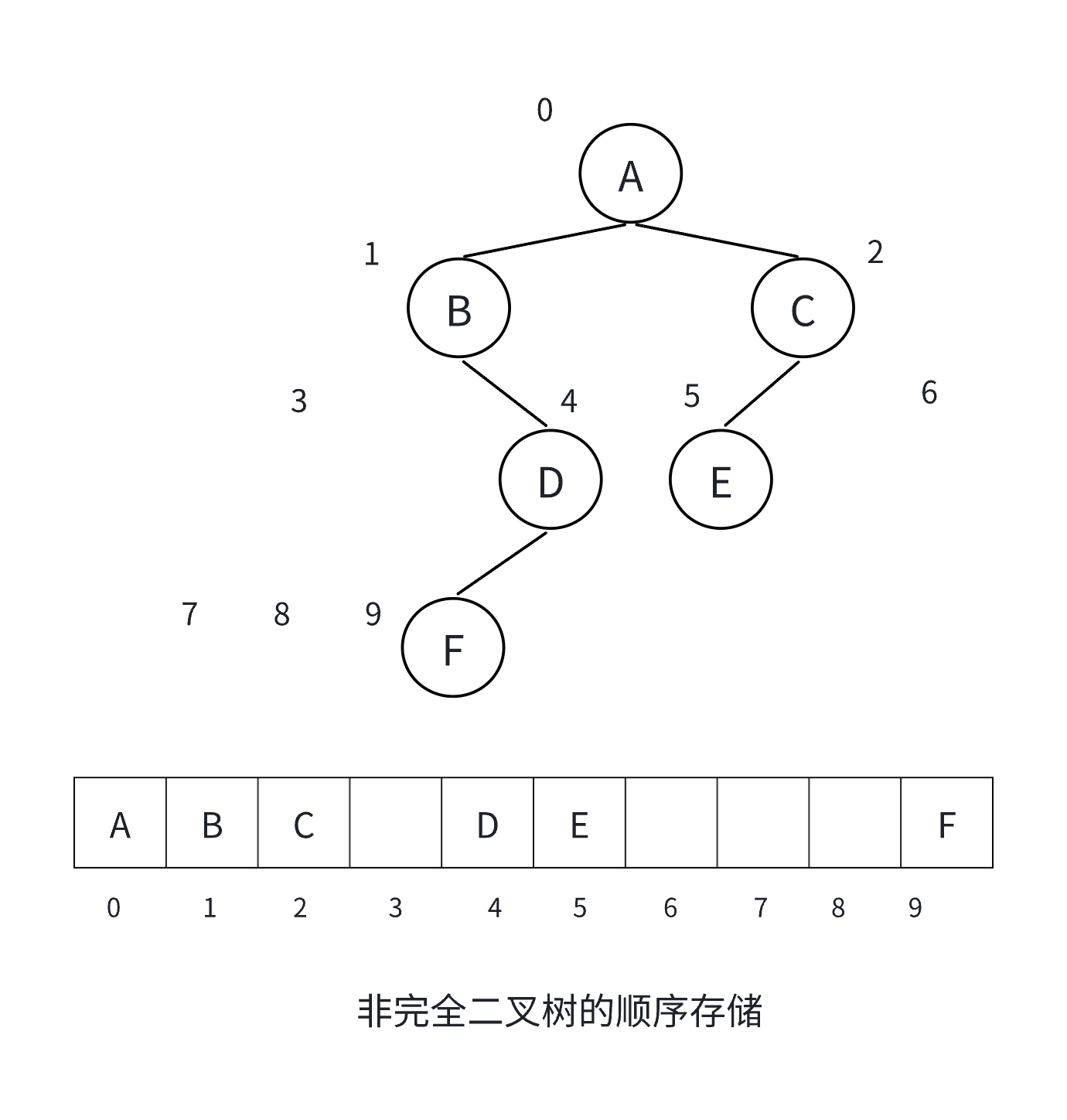
我们从图中可以看到,非完全二叉树会有空间浪费。
现实中我们通常把堆(⼀种⼆叉树)使⽤顺序结构的数组来存储,需要注意的是这⾥的堆和操作系统虚拟进程地址空间中的堆是两回事,⼀个是数据结构,⼀个是操作系统中管理内存的⼀块区域分段。
2.实现顺序结构二叉树
堆是⼀种特殊的⼆叉树,具有⼆叉树的特性的同时,还具备其他的特性。
2.1何为堆
堆是一种树形数据结构,每个父节点都大于或等于(最大堆)或者小于或等于(最小堆)其子节点,根节点的值是堆中所有元素的最大值或最小值。
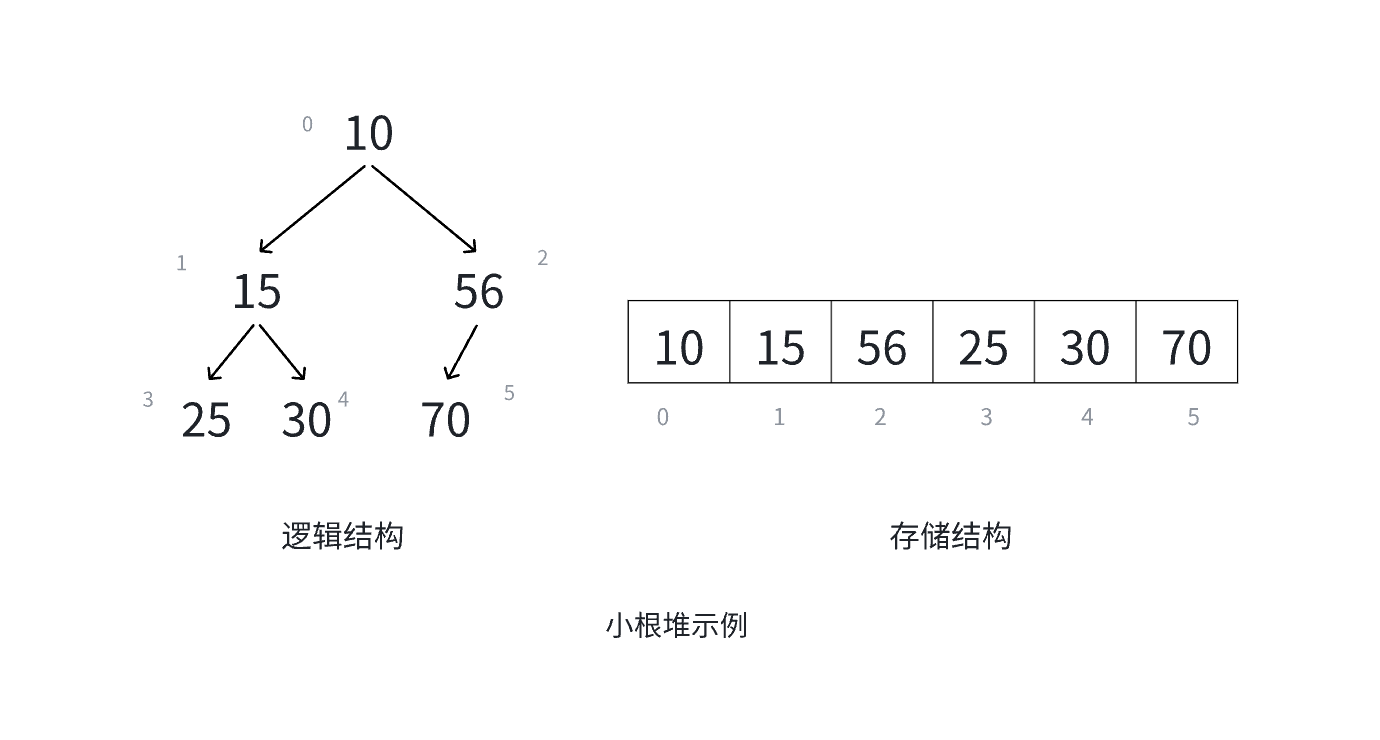
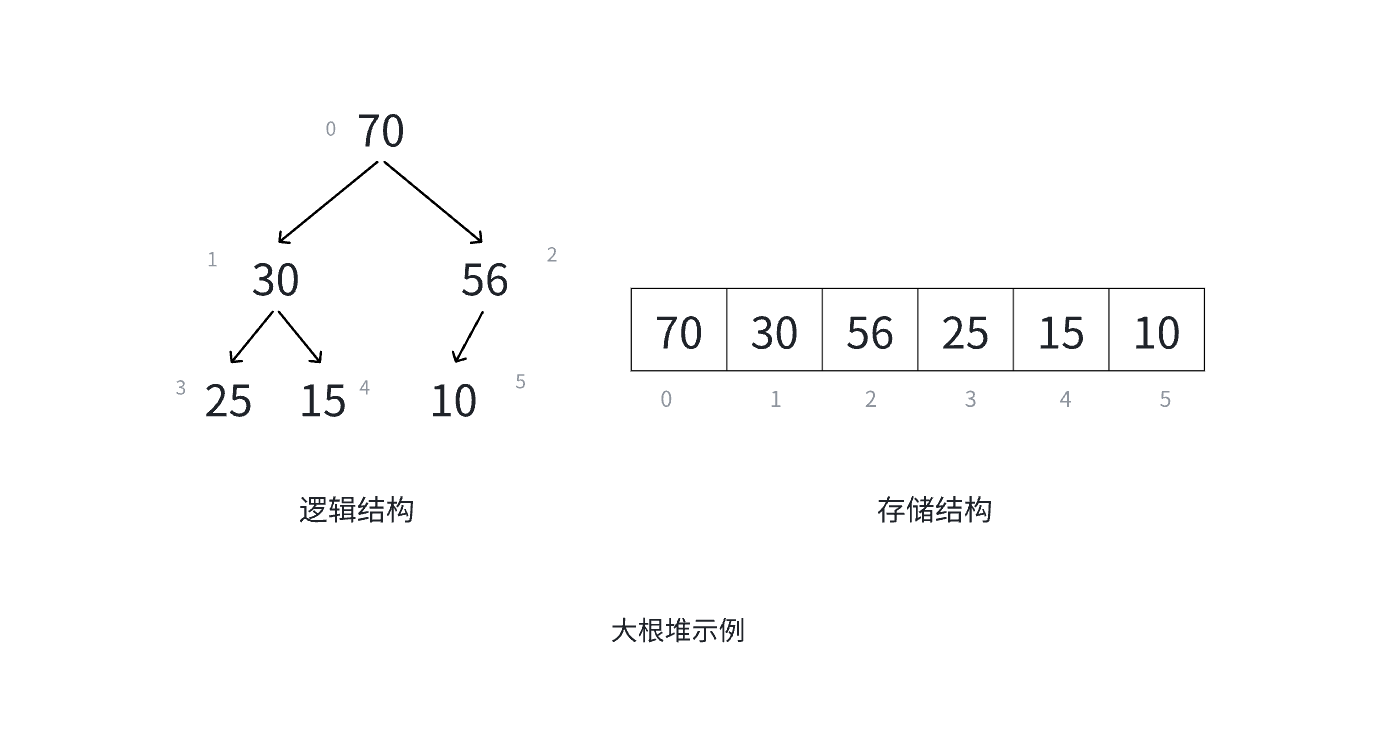
2.2堆的性质
- 堆中某个结点的值总是不⼤于或不⼩于其⽗结点的值;
- 堆总是⼀棵完全⼆叉树
在用代码实现前,我们还需要知道一些二叉树的性质:

2.3堆的定义
typedef int HpDataType;
typedef struct Heap {HpDataType* arr;int size;int capacity;
}Hp;
size表示有效个数
capacity表示可用容量
2.3堆的初始化与销毁
//初始化
void HpInit(Hp* php) {assert(php);php->arr = NULL;php->size = php->capacity = 0;
}
//销毁
void HpDestroy(Hp* php) {assert(php);if (php->arr)free(php->arr);php->size = php->capacity = 0;
}
3.1向上调整算法
当我们往堆中添加数据时,怎么能使数据自动校正自己的位置,使得其插入后任然满足是一个堆。
对于大堆:
//向上调整
void AdjustUp(HpDataType* arr, int child) {int parent = (child - 1) / 2;while (child > 0) {if (arr[child] > arr[parent]) {Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}
每一次和父节点比较,如果比父节点大则交换并使父节点变子节点,再找新的父节点比较。否则退出循环。
3.2向下调整算法
对于大堆:
//向下调整
void AdjustDown(HpDataType* arr, int parent, int n) {int child = 2 * parent + 1;while (child < n) {//对于两个子节点,先找到较大的一个,再与之比较if (child + 1 < n && arr[child] < arr[child + 1]) {child++;}if (arr[child] > arr[parent]) {Swap(&arr[child], &arr[parent]);parent = child;child = 2 * parent + 1;}else {break;}}
}
4.入堆
//入堆
void HpPush(Hp* php,HpDataType x) {assert(php);//空间不够增容if (php->size == php->capacity) {int newcapacity = php->capacity == 0 ? 4 : 2 * (php->capacity);HpDataType* tmp = (HpDataType*)realloc(php->arr, newcapacity * sizeof(HpDataType));if (tmp == NULL) {perror("realloc fail");exit(1);}php->arr = tmp;php->capacity = newcapacity;}php->arr[php->size++] = x;//向上调整AdjustUp(php->arr, php->size - 1);
}
5.出堆
出堆指的是堆顶元素出去。
//出堆
void HpPop(Hp* php) {assert(!HpEmpty(php));Swap(&php->arr[0], &php->arr[php->size - 1]);php->size--;//重新向上调整AdjustUp(php->arr, php->size - 1);//如果使用向下调整,换成 AdjustDown(php->arr, 0, php->size);
}
完
如果发现错误,欢迎打在评论区。
主页还有更多优质内容OvO
