01 神经网络简介
1 单个神经元如何感知信息
1.1 激活函数
感知信息的基本条件是对不同的输入能够区分
σ(x)={1x≥T0x<T,
\sigma(x)=\left\{\begin{array}{ll}
1 & x \geq T \\
0 & x<T
\end{array},\right.
σ(x)={10x≥Tx<T,
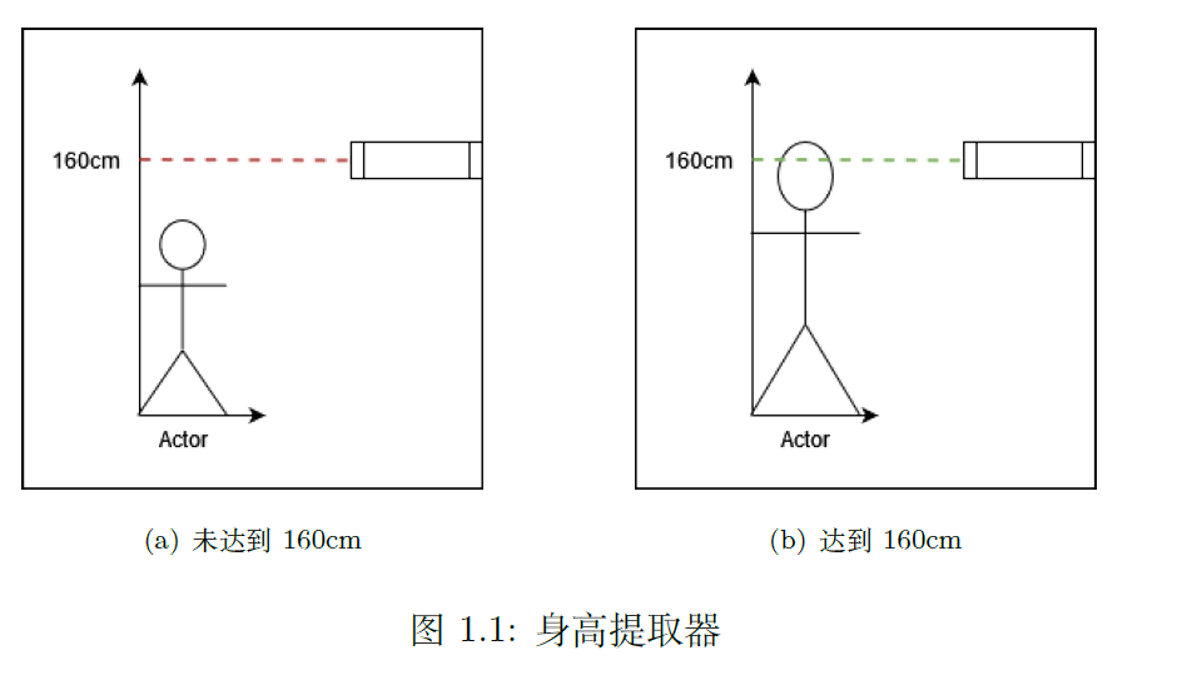
以身高提取器来理解激活函数σ(x)\sigma(x)σ(x):
- 当小于160cm,信号接收器接收到反射信号;
- 当大于等于160cm,信号接收器接收不到反射信号。
1.2 权重
一个预测股票升降的例子:假设A 有两个朋友,B 和C。A 自己有一个判断值a0a_0a0,同时接收到了B和C的信息,分别记为b和c。因此,A接收到的信息为:
a=λ1b+λ2c+a0
a = \lambda_1b+ \lambda_2c + a_0
a=λ1b+λ2c+a0
如果B是一个经济学家,而C 是一个普通人,则有,λ1λ_1λ1>λ2λ_2λ2>0。
我们可以把这类收集信息的方式推广到一般的形式:
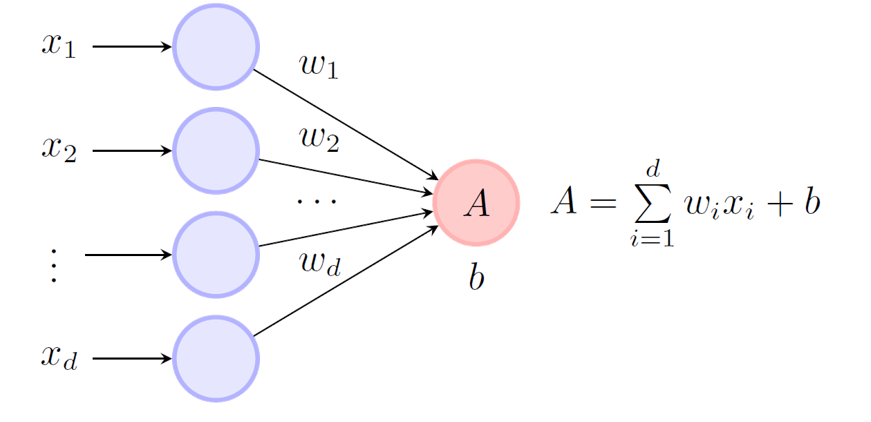
w1x1+⋯+wdxd+b=(w1,⋯ ,wd)⋅(x1,⋯ ,xd)+b=wTx+b
\begin{array}{l}
w_{1} x_{1}+\cdots+w_{d} x_{d}+b \\
=\left(w_{1}, \cdots, w_{d}\right) \cdot\left(x_{1}, \cdots, x_{d}\right)+b \\
=\boldsymbol{w}^{T} \boldsymbol{x}+b
\end{array}
w1x1+⋯+wdxd+b=(w1,⋯,wd)⋅(x1,⋯,xd)+b=wTx+b
单个神经元的输出为:
σ(wTx+b)
\sigma(\boldsymbol{w}^{T} \boldsymbol{x}+b)
σ(wTx+b)
σ(⋅)\sigma(\cdot)σ(⋅)通常称为激活函数。
一个预测股票升降的例子:假设A 有两个朋友,B 和C。A 自己有一个判断值a0a_0a0,同时接收到了B和C的信息,分别记为b和c。因此,A接收到的信息为:
a=λ1b+λ2c+a0
a = \lambda_1b+ \lambda_2c + a_0
a=λ1b+λ2c+a0
如果B是一个经济学家,而C 是一个普通人,则有,λ1λ_1λ1>λ2λ_2λ2>0。
2 单层神经网络
简单地把多个神经元堆在一起,我们就可以得到单层神经网络:
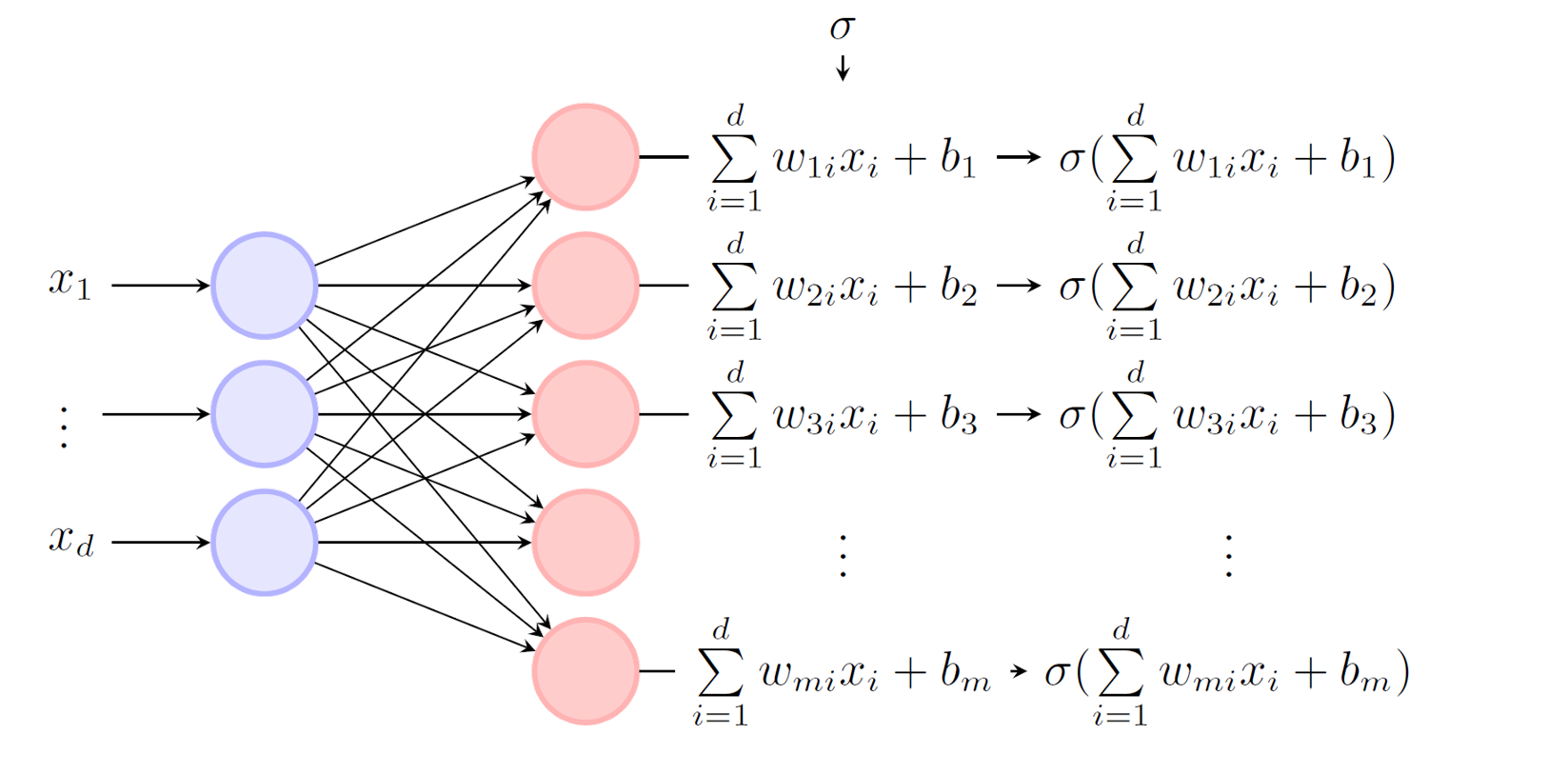
神经网络的高维输出:
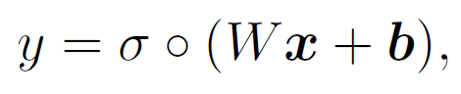
参数的矩阵形式:
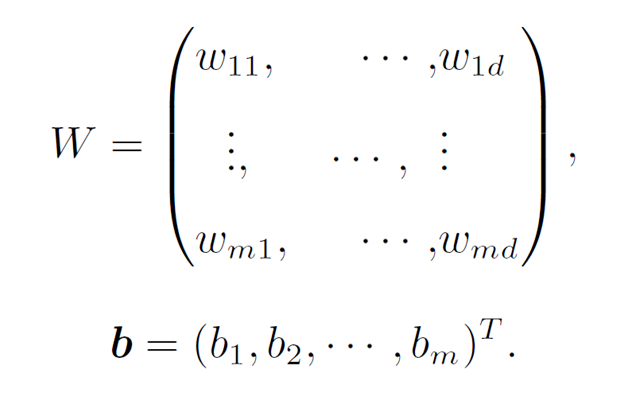
∘ 表示对每个元素作用:
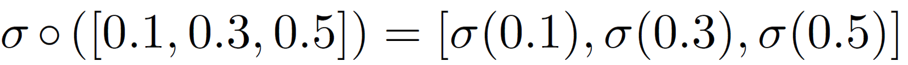
2.1 设计功能
考虑输入是两维的,x1,x2∈{0,1}2x_1,x_2∈\{0,1\}^2x1,x2∈{0,1}2:
σ(x)={1x1+x2≥T0x1+x2<T,
\sigma(x)=\left\{\begin{array}{ll}
1 & x_1 + x_2 \geq T \\
0 & x_1 + x_2<T
\end{array},\right.
σ(x)={10x1+x2≥Tx1+x2<T,
- AND: T=2;即11为1,00,01,10都是0;
- Or: T=1;即00为0,01,10,11都是1;
- Not: T=0;σ(x)=−xσ(x)=−xσ(x)=−x,这里还没理解到是如何运作的?
2.2 局限性
单层神经网络是无法做好XOR问题:
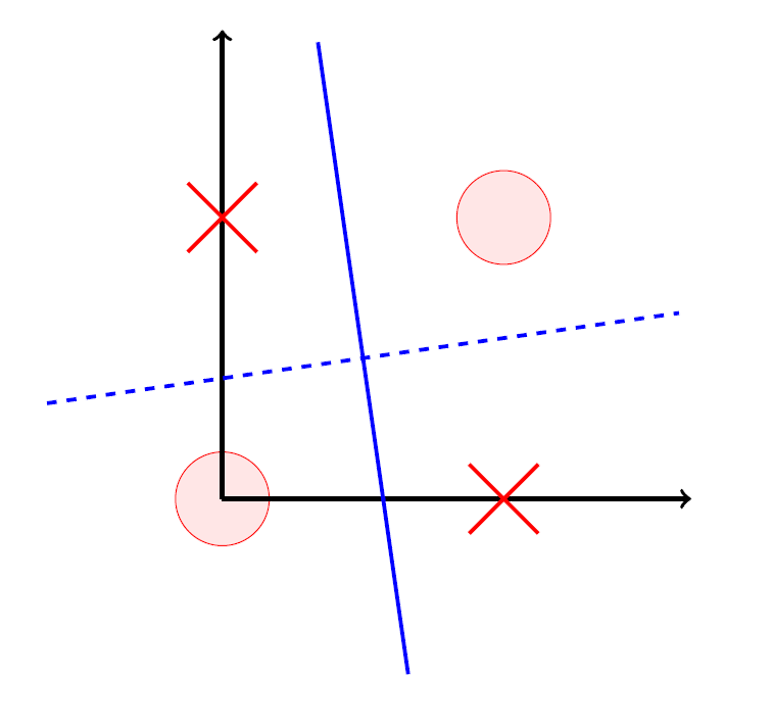
3 多层神经网络
多层神经网络是在一层神经网络的基础上堆叠起来的。
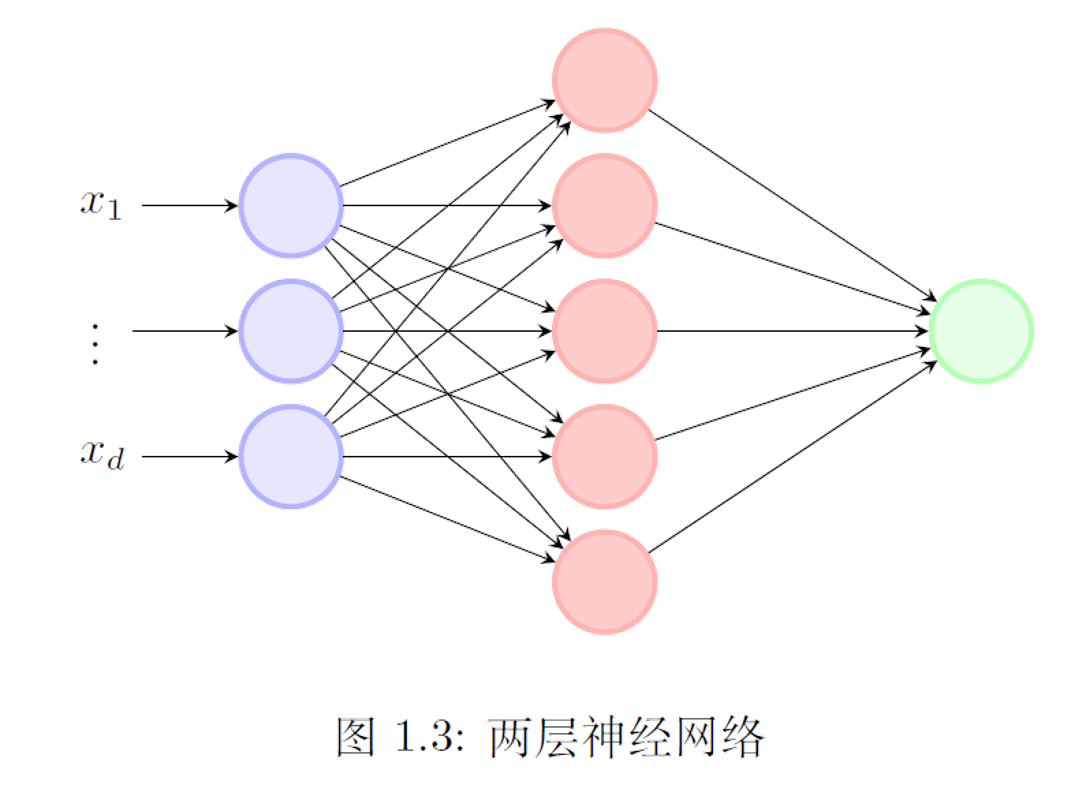
3.1 解XOR问题
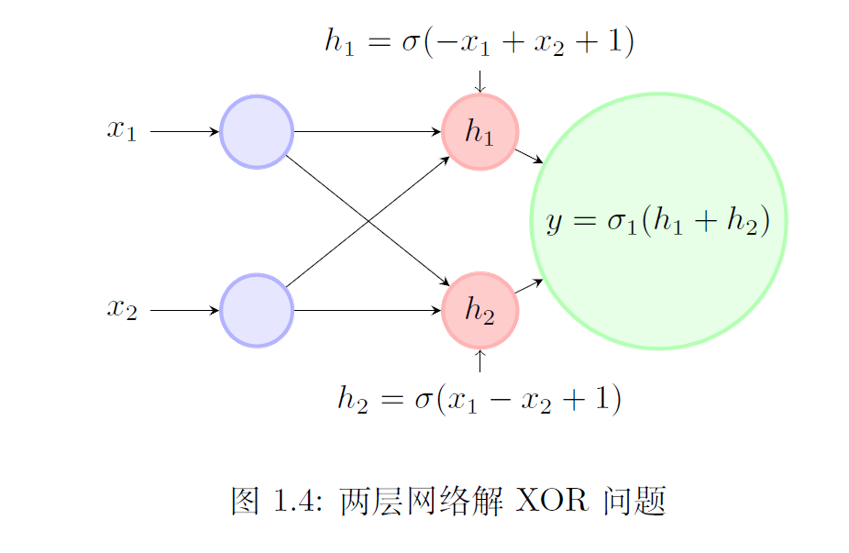
- 假设,y=σ(h1+h22)y=σ(\frac{ℎ_1+ℎ_2}{2})y=σ(2h1+h2)
- 代入(0,0), (1,1),则y=σ(1)=1y=σ(1)=1y=σ(1)=1。
- 代入(1,0), (0,1),则y=σ(1/2)=0y=σ(1/2)=0y=σ(1/2)=0。
性质
- 两层网络具有万有逼近定理(Cybenko 1989):激活函数是非多项式的非线性函数
- 多项式函数是否有万有逼近定理?
- 为什么激活函数不能是多项式函数?
- 万有逼近定理对实际问题有什么帮助?
- 万有逼近定理是否足够让我们使用神经网络?
- 多层神经网络只是众多机器学习方法中的一种!
