机器学习基础-day02-K近邻算法

1 KNN算法介绍

K最近邻(K-Nearest Neighbor,KNN)分类算法是数据挖掘分类技术中最简单的方法之一，是著名的模式识别统计学方法，在机器学习分类算法中占有相当大的地位。它是一个理论上比较成熟的方法。既是最简单的机器学习算法之一，也是基于实例的学习方法中最基本的，又是最好的文本分类算法之一。

定义：KNN(K-Nearest Neighbor) k个最近的邻居，即每个样本都可以用它最接近的k个邻居来代表,KNN算法属于监督学习方式的分类算法，通过测量不同数据点之间的距离进行分类或回归分析。

原理-“近朱者赤”：基于实例的学习(instance-based learning)，属于懒惰学习(Lazy learning)，即KNN没有显式的学习过程，也就是说没有训练阶段（仅仅是把样本保存起来，训练时间开销为零）它是通过测量不同数据点的之间的距离进行分类或者回归。

特点： KNN算法简单易懂，易于实现；

            无需训练阶段，直接进行分类或者回归；

            适用于多分类问题；

            对数据集的大小和维度不敏感

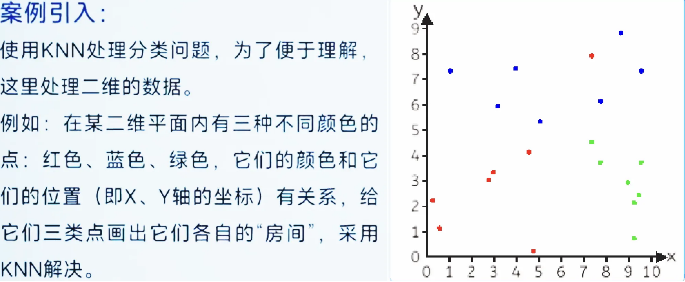
图中的点通常代表已知样本。在KNN算法的上下文中，这些点是已经标记好的训练数据，每个点都有一个对应的类别标签（在图中用不同的颜色表示）。这些已知样本用于帮助算法确定新数据点（待分类样本-坐标系中任何一个位置中可能出现的点）的类别。

1.1 决策边界

定义：决策边界是分类算法中用于区分不同类别的虚拟边界，通俗讲就是在什么范围内归为当前类。

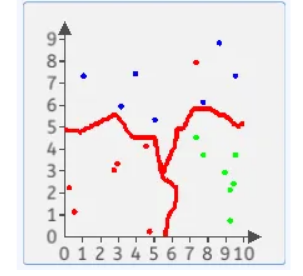
边界效果：决策边界是否合理，直接影响到分类效果的好坏。

KNN与决策边界:

KNN算法通过计算待分类样本与已知样本之间的距离，找到最近的K个样本，并根据这些样本的类型信息进行投票，以确定待分类样本的类别。

如何绘制决策边界：

为了绘制出决策边界，预测的数据点是二维坐标中所有的点，为了降低计算量，需要对这些预测点进行“采样”，因此每隔距离x取一个点（预测数据点）。

1.2 距离选择

k近邻法(K-Nearest Neighbor,KNN)：计算新的点(测试点)到每一个已知点(标签点)的距离，并比对距离，使用不同的距离公式会得到不同的分类效果。后面会介绍一下常用的距离计算方法。

2 KNN三要素

KNN算法有三要素：1.K值选择；2.距离选择；3.分类规则选择。

2.1 K值选择

算法中的K在KNN中被称为超参数（Hyper parameter，需要人为确定的参数），它指的是在进行预测时，考虑的最近邻样本点的数量。

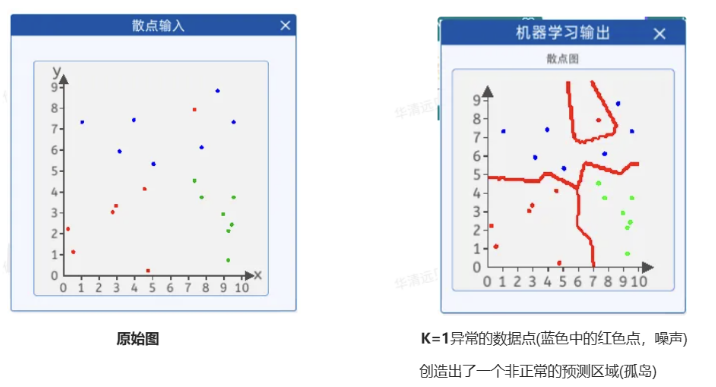
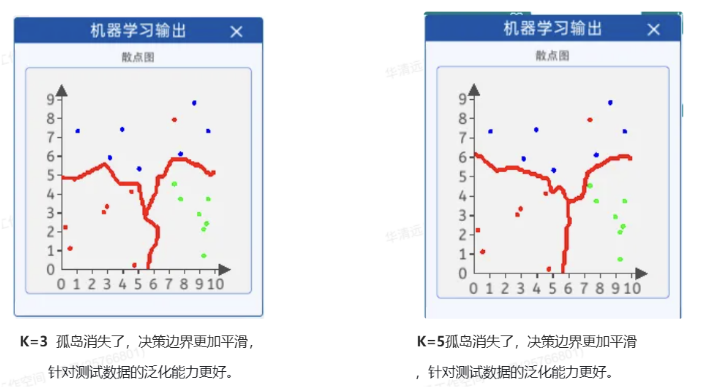
K值选择存在的问题：

K值过小：

优点：复杂的数据集，K值较小可能会提供更详细的决策边界，因为模型更加灵活。

缺点：容易受到局部结构的影响，模型受噪声和异常值的影响更大。

选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合。

K值过大：

优点：考虑了更多的全局信息，对于平滑的数据集，较大的K值可以提供更稳定的决策边界。

缺点：对于复杂的数据集，较大的K值可能会导致模型过于简单，无法准确捕获数据的局部特征。

选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。

极端情况，K=N（N为训练样本个数），则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。

如何科学地选择最有K值？（认识一下，初期学习不用）

在实际应用中，K值一般取一个比较适中的数值，例如采用交叉验证法。简单来说，就是把训练数据（图上红绿蓝点）在分成两组：训练集和验证集，通过计算来选择最优的K值。

2.2 距离选择

先使用欧氏距离，后面单独介绍其他距离选择方式。

2.3 分类规则选择

分类问题：对新的实例，根据与之相邻的k个训练实例的类别，通过多数表决法或者加权多数表决法等方式进行预测

回归问题：对新的实例，根据与之相邻的K个训练实例的标签，通过均值计算进行预测。

3 KNN算法步骤

输入：训练数据集T={(x1,y1),(x2,y2)...(xn,yn)}，

        x1为实例的特征向量，

        yi={c1,c2,c3...ck}为实例类别。

输出：测试实例(xm,ym)所属的类别yi。

步骤：

(1) 选择参数K

(2) 计算未知实例与所有已知实例的距离(可选择多种计算距离的方式)

(3) 选择最近K个已知实例

(4) 根据少数服从多数的投票法则(Majority-voting),让未知实例归类为K个最近邻样本中最多数的类别。

4 KNN算法思想

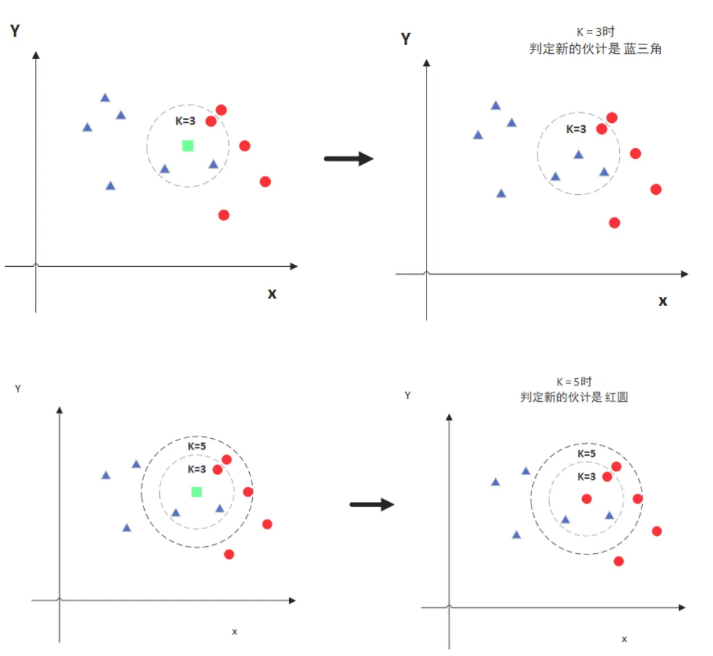
图中绿色的点就是我们要预测的那个点，假设K=3。那么KNN算法就会找到与它距离最近的三个点（这里用圆圈把它圈起来了），看看哪种类别多一些，比如这个例子中是蓝色三角形多一些，新来的绿色点就归类到蓝三角了。

代码：使用JupyterLab写代码

加深练习：

把上述KNN算法的数据量从21（3分类）改为88（4分类），采样1000*1000，x y轴范围改为0-100