当前位置：首页 > news >正文

leetcode46.全排列

news 2025/9/2 13:36:35

一、题目描述

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数互不相同

二、题目解析

1、回溯法
采用试错思想，每次从剩余元素中取一个没取过的元素，
形成一个排列后，逐层向上回溯，寻找下一个排列。
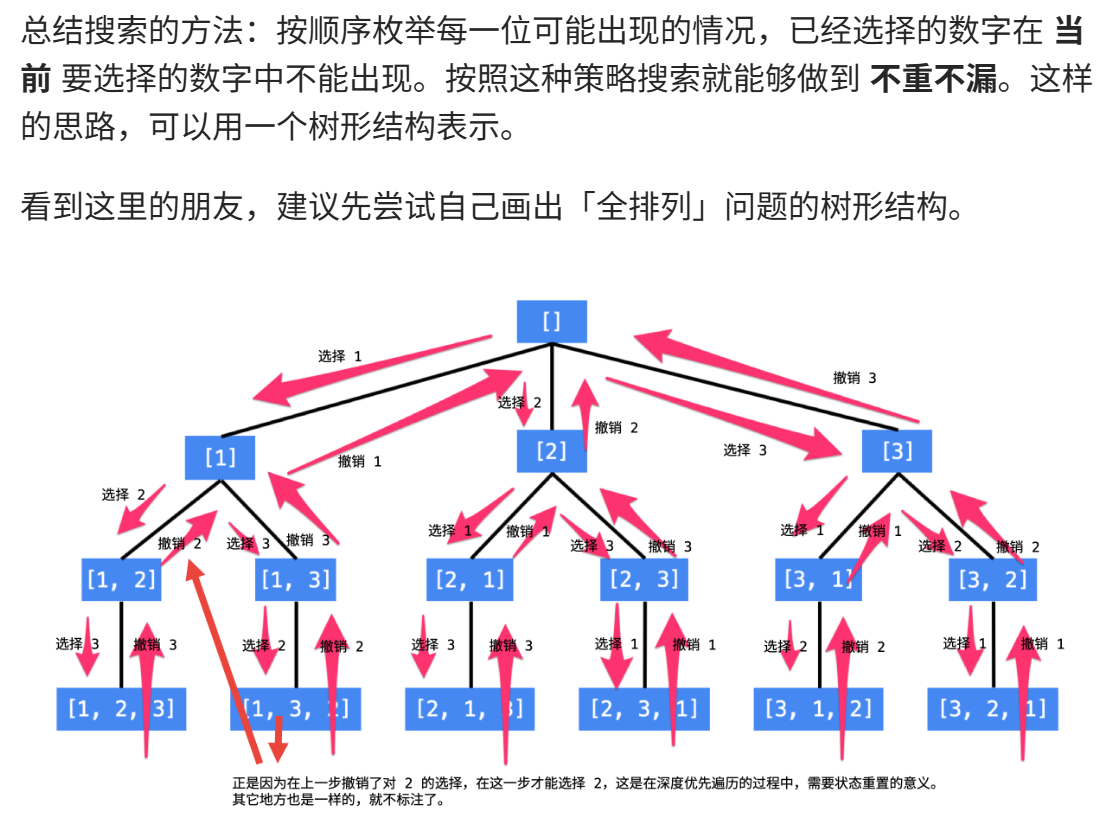
在这里插入图片描述
递归的终止条件是：一个排列中的数字已经选够了，因此我们需要一个变量来表示当前程序递归到第几层，我们把这个变量叫做 depth，或者命名为 index ，表示当前要确定的是某个全排列中下标为 index 的那个数是多少；
布尔数组 used，初始化的时候都为 false 表示这些数还没有被选择，当我们选定一个数的时候，就将这个数组的相应位置设置为 true ，这样在考虑下一个位置的时候，就能够以 O(1) 的时间复杂度判断这个数是否被选择过，这是一种「以空间换时间」的思想。

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;public class Solution {public List<List<Integer>> permute(int[] nums) {int len = nums.length;// 使用一个动态数组保存所有可能的全排列List<List<Integer>> res = new ArrayList<>();if (len == 0) {return res;}boolean[] used = new boolean[len];Deque<Integer> path = new ArrayDeque<>(len);dfs(nums, len, 0, path, used, res);return res;}private void dfs(int[] nums, int len, int depth,Deque<Integer> path, boolean[] used,List<List<Integer>> res) {if (depth == len) {//这里不可直接添加path，java中path是值传递，是列表对象的地址，递归过程中始终指向的是同一块内存。path指向的对象在不断地增加和删除元素，深度优先遍历完成后回到了根结点，成为空列表，故最终res的结果是5个空列表。//我们需要的是快照，所以这里需要拷贝一下res.add(new ArrayList<>(path));return;}//// 在非叶子结点处，产生不同的分支，这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。for (int i = 0; i < len; i++) {if (!used[i]) {path.addLast(nums[i]);used[i] = true;System.out.println("  递归之前 => " + path);dfs(nums, len, depth + 1, path, used, res);//// 注意：下面这两行代码发生 「回溯」used[i] = false;path.removeLast();System.out.println("递归之后 => " + path);}}}
}

时间复杂度：O(n×n!)，其中 n 为序列的长度。
（我们需要将当前答案使用 O(n) 的时间复制到答案数组中，相乘得时间复杂度为 O(n×n!)）
空间复杂度：O(n)，其中 n 为序列的长度。除答案数组以外，递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，这里可知递归调用深度为 O(n)。

在这里插入图片描述
2、插入法
从第一个元素开始，每加入一个元素，穷举新加入的元素能出现的所有位置，一直加到最后一个元素。

以 {1, 2, 3} 为例，先取1，全排列为{1}，2进来后，全排列变为 {{1,2},{2,1}}，3进来后，全排列变为{{3,1,2},{1,3,2},{1,2,3}, {3,2,1}, {2,3,1}, {2,1,3}}，这就是最后的结果，这样应该更好理解一些（后一次的全排列就是让新元素在原来的全排列的每个排列中的所有位置都出现一次）。

class Solution {public List<List<Integer>> permute(int[] nums) {List<List<Integer>> result = new ArrayList<>();List<Integer> list = new ArrayList<>();list.add(nums[0]);result.add(list);//初始排列中仅包含nums[0], 然后挨个将nums中的其它元素加入排列for (int i = 1; i < nums.length; i++) {permute(result, nums[i]);}return result;}private void permute(List<List<Integer>> result/*当前元素个数下的所有排列*/, int newNum/*新加入的元素*/) {int n = result.size();//算一下当前有多少种排列，然后从后往前删除for (int i = n - 1; i >= 0; i--) {List<Integer> subList = result.get(i);int subSize = subList.size();//将新元素挨个插入当前排列的 0~len ，就是新元素在当前排列种可能出现的所有位置，然后将这些新的排列也加入result，作为下一新元素进来时的基础while (subSize >= 0) {List<Integer> newList = new ArrayList<>(subList);newList.add(subSize--, newNum);result.add(newList);}result.remove(i);}}
}

在这里插入图片描述