使用 Google OR-Tools 轻松解决复杂优化问题（如排程优化）

之前有一篇Pyomo、PuLP 和 OR-Tools 解决约束优化问题效率对比,对比了几个同样的优化的python库。本篇文章Solve Complex Optimization Problems (like Schedule Optimization) with easy to use Google OR Tools适合对优化问题感兴趣的读者，特别是初学者。文章的亮点在于介绍了Google OR-Tools作为一个强大的开源工具，能够高效解决复杂的优化问题，如调度和路线规划。它通过简洁的Python代码示例，使读者能够快速上手。

---

---

有些问题并非关乎预测未来，而是要在数量惊人的选项中找到最佳决策。这正是优化的用武之地。如果你在 Python 中进行开发，Google OR-Tools 是你可以使用的最强大的开源工具包之一。

从优化送货卡车路线到安排生产线上的机器，OR-Tools 将最先进的算法带到你的指尖。我们将探讨：

• OR-Tools 是什么以及它为何有用
• 它能解决的常见优化问题类型
• 一个关于线性规划的 Python 实践示例

1 什么是 Google OR-Tools？

OR-Tools 是由 Google 开发的一套开源组合优化套件。它有助于解决那些可能解的数量极其庞大——远超暴力搜索范围的问题。OR-Tools 转而使用高级求解器，高效地寻找最优或接近最优的解。

1.1 OR-Tools 可以解决的示例问题：

• 车辆路径规划：为车队规划最优配送路线，同时遵守重量限制和配送时间窗。
• 排程：根据优先级和时间限制将任务分配给资源。
• 箱子装载：将不同尺寸的物品高效地装入容量有限的容器中。
• 图优化：最短路径、最大流和分配问题。

1.2 什么是优化问题？

优化问题总是包含：

1. 目标函数 — 需要优化的量（最小化成本、最大化利润等）。
2. 约束条件 — 对可能解的限制。
3. 可行解 — 满足所有约束条件的解。

示例：
一家航运公司必须将包裹分配给卡车并规划其路线，以最小化总成本。

• 目标：最小化成本（燃料、时间等）。
• 约束：卡车容量、交货期限。
• 可行解：满足所有约束，但不一定是成本最低的。
• 最优解：在所有可行解中成本最低的解。

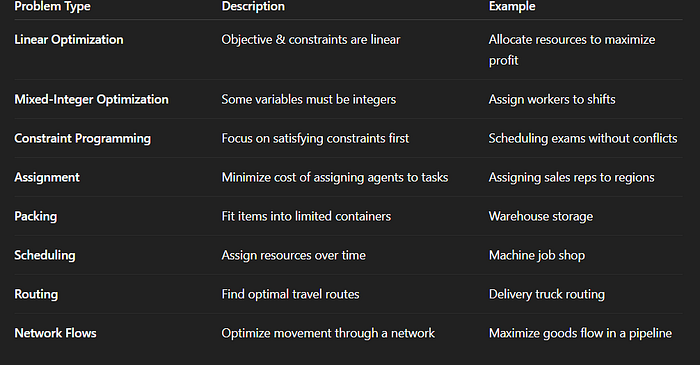
1.2 OR-Tools 解决的问题类型

2 实践：在 Python 中解决线性优化问题

让我们通过一个使用 OR-Tools 的简单线性规划示例。

问题：
最大化：
$3x+y$
受限于：
$0\le x\le 1$
$0\le y\le 20$
$x+y\le 2x$

步骤 1：安装 OR-Tools

pip install ortools

步骤 2：Python 代码

from ortools.init.python import init
from ortools.linear_solver import pywraplpdef main():print("Google OR-Tools version:", init.OrToolsVersion.version_string())solver = pywraplp.Solver.CreateSolver("GLOP")if not solver:print("Solver not created.")returnx = solver.NumVar(0, 1, "x")y = solver.NumVar(0, 2, "y")print("Number of variables =", solver.NumVariables())infinity = solver.infinity()constraint = solver.Constraint(-infinity, 2, "ct")constraint.SetCoefficient(x, 1)constraint.SetCoefficient(y, 1)print("Number of constraints =", solver.NumConstraints())objective = solver.Objective()objective.SetCoefficient(x, 3)objective.SetCoefficient(y, 1)objective.SetMaximization()result_status = solver.Solve()if result_status != pywraplp.Solver.OPTIMAL:print("No optimal solution found.")returnprint("Solution:")print("Objective value =", objective.Value())print("x =", x.solution_value())print("y =", y.solution_value())print(f"Solved in {solver.wall_time()} ms")
if __name__ == "__main__":main()

步骤 3：运行

python program.py

输出：

Solution:
Objective value = 4.0
x = 1.0
y = 1.0

3 为什么在数据科学中使用 OR-Tools？

• 速度：针对巨大搜索空间的高效算法。
• 灵活性：支持线性规划、整数规划、约束编程等。
• 实战就绪：在 Google 规模的路由和排程问题中得到应用。

3.1 主要收获

• 优化 ≠ 预测 — 它是在给定约束条件下做出最佳决策。
• Google OR-Tools 可以解决各种优化问题 — 从排程到路径规划再到装箱。
• 从线性规划开始，然后探索更高级的求解器，如约束编程或混合整数规划。

3.2 完整代码示例：使用 OR-Tools 解决护士排班问题

排程问题无处不在——从将送货卡车分配到路线，到管理工厂中的机器作业。在这个例子中，我们将探讨一个受现实世界启发的医院护士排班问题。

场景：
医院主管需要在3 天内安排4 名护士，并遵循以下规则：

1. 每天三班（每班 8 小时）。
2. 每班一名护士，并且每名护士每天工作不超过一班。
3. 在三天内，每名护士至少工作两班。

3.2.1 步骤 1：导入所需库

我们将使用 OR-Tools 的 cp_model 模块中的约束编程 (CP)：

from ortools.sat.python import cp_model

3.2.2 步骤 2：定义问题数据

num_nurses = 4
num_shifts = 3
num_days = 3
all_nurses = range(num_nurses)
all_shifts = range(num_shifts)
all_days = range(num_days)

3.2.3 步骤 3：创建模型和变量

我们将创建布尔变量，其中：

如果护士 [n] 在第 [d] 天工作班次 [s]，则 $shifts[(n,d,s)]=1$

model = cp_model.CpModel()shifts = {}
for
````pythonn in all_nurses:for d in all_days:for s in all_shifts:shifts[(n, d, s)] = model.NewBoolVar(f"shift_n{n}_d{d}_s{s}")

3.2.4 步骤 4：添加约束

1. 每班次恰好有一名护士

for d in all_days:for s in all_shifts:model.AddExactlyOne(shifts[(n, d, s)] for n in all_nurses)

2. 每名护士每天工作不超过一班

for n in all_nurses:for d in all_days:model.AddAtMostOne(shifts[(n, d, s)] for s in all_shifts)

3. 每名护士总共至少工作两班

我们根据总需求计算每名护士的最小和最大班次：

min_shifts_per_nurse = (num_shifts * num_days) // num_nurses
max_shifts_per_nurse = (min_shifts_per_nurseif (num_shifts * num_days) % num_nurses == 0else min_shifts_per_nurse + 1
)for n in all_nurses:shifts_worked = [shifts[(n, d, s)] for d in all_days for s in all_shifts]model.Add(sum(shifts_worked) >= min_shifts_per_nurse)model.Add(sum(shifts_worked) <= max_shifts_per_nurse)

3.2.5 步骤 5：创建解决方案打印回调

这让我们能够检查多个有效的排班表：

class NursesPartialSolutionPrinter(cp_model.CpSolverSolutionCallback):def __init__(self, shifts, num_nurses, num_days, num_shifts, limit):cp_model.CpSolverSolutionCallback.__init__(self)self._shifts = shiftsself._num_nurses = num_nursesself._num_days = num_daysself._num_shifts = num_shiftsself._solution_count = 0self._solution_limit = limitdef on_solution_callback(self):self._solution_count += 1print(f"Solution {self._solution_count}")for d in range(self._num_days):print(f"Day {d}")for n in range(self._num_nurses):working = Falsefor s in range(self._num_shifts):if self.Value(self._shifts[(n, d, s)]):working = Trueprint(f"  Nurse {n} works shift {s}")if not working:print(f"  Nurse {n} does not work")print()if self._solution_count >= self._solution_limit:self.StopSearch()

3.2.6 步骤 6：求解并打印解决方案

solver = cp_model.CpSolver()
solver.parameters.enumerate_all_solutions = True
solution_printer = NursesPartialSolutionPrinter(shifts, num_nurses, num_days, num_shifts, limit=5)
solver.Solve(model, solution_printer)

3.2.7 示例输出

Solution 1
Day 0Nurse 0 does not workNurse 1 works shift 0Nurse 2 works shift 1Nurse 3 works shift 2
Day 1Nurse 0 works shift 2Nurse 1 does not workNurse 2 works shift 1Nurse 3 works shift 0
Day 2Nurse 0 works shift 2Nurse 1 works shift 1Nurse 2 works shift 0Nurse 3 does not work

这个例子展示了 OR-Tools 中的约束编程如何用几行代码建模和解决复杂的排程问题。与传统的暴力方法不同，OR-Tools 在遵守所有约束的同时高效地搜索可行解——这使其非常适合实际世界的排程、时间表和资源分配问题。