当前位置：首页 > news >正文

【线性代数基础 | 那忘算9】基尔霍夫（拉普拉斯）矩阵矩阵—树定理证明 [详细推导]

news 2025/9/1 5:48:45

~~之前学的不扎实导致现在还得回来再学。~~

专栏指路：《再来一遍一定记住的算法（那些你可能忘记了的算法）》

前置知识：

生成树：在一个无向连通图中，能够连接所有顶点的树结构。

点的度数：与这个点相连的边有多少条。

矩阵及矩阵乘法定义。

没学过行列式的建议看我写的这个

（注意行列式这个非常重要！！一定要会！）

秩：矩阵的线性无关的行向量数量，高斯消元后有几个非零行，秩就是几。

前导：

求出一个无向连通图的生成树并不难，但如果我们想求出图的所有生成树数量呢？

（如果你还不知道怎么求生成树，也许可以看看我的这篇最小生成树）

1.基尔霍夫矩阵

基尔霍夫矩阵（Kirchhoff matrix），由德国物理学家古斯塔夫·基尔霍夫发明。

后因定义与数学中的拉普拉斯矩阵高度重合，所以两者在中文语境里是相同的。

（后文中出现的拉普拉斯矩阵都指基尔霍夫矩阵）

定义：当 $i=j$ 时， $L[i][j]$ 为 $i$ 点的度数。

当 $i!=j$ 时，如果两点有边相连， $L[i][j]$ 为节点 i 和 j 之间边数的负值

（但因为重边一般会特判，直接等于 $-1$ 也可以），反之为 $0$ 。

也写作 $L=D-A$ 。

其中 $L$ 是拉普拉斯矩阵， $D$ 是度矩阵（只有 $D[i][i]$ 不为 $0$ ， $D[i][i]$ = 点 $i$ 的度数）。

$A$ 是邻接矩阵（当 $i=j$ 时为 $0$ ;

其他时候，如果两点有边相连， $A[i][j]$ 为 $1$ ，反之为 $0$ ）。

通常教程会告诉你：

啊，矩阵树定理就是给无向连通图建个基尔霍夫矩阵，去掉某一行某一列，

再求个行列式，就是这个图的生成树数量啦！

道理都懂，但是生成树数量为什么会和行列式挂钩啊！！

2.拉普拉斯矩阵和关联矩阵

要想探究上面那个问题，我们要引入一个新的概念——

关联矩阵：称 $B$ 是一个 $n*m$ 矩阵，其中 $B[i][j]=1$ 如果顶点 i 是边 j 的一个端点，

如果 $B[i][j]=-1$ 顶点 i 是边 j 的另一个端点（对每条边任意指定方向），否则 $B[i][j]=0$ 。

对于拉普拉斯矩阵 $L$ ，我们有：

$L=B*B^T$

等等，这个 $B^T$ 是啥？

它是矩阵转置（Transpose）是指将矩阵的行和列互换的操作。

对于一个矩阵 $B$ ，其转置记为 $B^T$ （也写作 $B'$ ）。

这么表示： $B^T[i][j]=B[j][i]$

比如说这个矩阵：

$\begin{vmatrix} 1 & 2 & 3 &4 \\ 8 & 7 & 6 & 5 \end{vmatrix}$

它的转置就是：

$\begin{vmatrix} 1 & 8\\ 2 & 7\\ 3 & 6\\ 4 & 5 \end{vmatrix}$

再说回这个式子：

$L=B*B^T$

分类讨论 $B*B^T$ 矩阵的每个元素：

对角元素 $(i = i)$ ：

$(B*B^T)[i][i]=\sum_{k=1}^{m}B[i][k]*B^T[k][i]=\sum_{k=1}^{n}B[i][k]^2$

= 顶点 i 的度数（因为每条与 i 相连的边贡献 $(\pm 1)^2$ ）

非对角元素 $(i \neq j)$ ：

$(B*B^T)[i][j]=\sum_{k=1}^{m}B[i][k]*B^T[k][j]=\sum_{k=1}^{n}B[i][k]*B[j][k]$

如果 i 和 j 之间有一条边，则该项为 -1（因为 $B[i][k]$ 和 $B[j][k]$ 符号相反）；

如果 i 和 j 之间没有边，则为 0。

这正好就是拉普拉斯矩阵 $L$ 的定义！

3.柯西—比内公式（Cauchy–Binet formula）及其应用

知道了这个 $L=B*B^T$ 有啥用呢？

我们还得上点科技——柯西—比内公式。

公式具体长这个样子：

设 $A$ 是 $m*n$ 矩阵， $B$ 是 $n*m$ 矩阵，其中 $m\leq n$ ，则有：

$det(AB)=\sum_{S}^{}det(A_s)*det(B_s)$

其中求和是对所有从 $\left \{ 1,2,...,n \right \}$ 中选取 $m$ 个元素的子集 $S$ 进行的，

$A_S$ 表示 $A$ 中选取 $S$ 对应的列组成的 $m*m$ 子矩阵，

$B_S$ 表示 $B$ 中选取 $S$ 对应的行组成的 $m*m$ 子矩阵。

我写的不严谨证明在这里，不建议看证明，直接背公式就行。

3.5.线性相关

在代入公式之前，我们还要对矩阵做处理。

设 $L[i]$ 为拉普拉斯矩阵去掉第 i 行第 i 列得到的 $(n-1)*(n-1)$ 矩阵。

$B[i]$ 为关联矩阵去掉第 i 行得到的 $(n-1)*m$ 矩阵。

为什么要这么做？首先我们知道生成树的边一定是 $n-1$ 条。

但这不算最重要的原因，最重要的是最开始是拉普拉斯矩阵是线性相关的！

线性相关的官方定义：在线性代数里，矢量空间的一组元素中，

若没有矢量用有限个其他矢量的线性组合所表示，则称为线性无关或线性独立。

反之则称为线性相关。

啊其实就是你用其他的元素一通计算捣鼓，能整出这个元素，那就是线性相关。

在矩阵中，把矩阵的每一行都看作一个 $n$ 维向量，

如果有一行和其他行向量加减/放缩的结果相等，

即这个矩阵线性相关。

而在拉普拉斯/关联矩阵里，如果有几行向量加起来是 0 向量，

那么这个矩阵就是线性相关，行列式为 0。

但是线性相关的矩阵行列式为什么为 0 ？

我们把矩阵的每一行都看作一个 $n$ 维向量，

而行列式就是这 $n$ 个向量张成的面积。

如果有两个向量线性相关，也就是一个是另一个的倍数，

那张出的面积肯定为 0。

（同学们可以自己试一下二阶和三阶矩阵，意会即可）

很明显，拉普拉斯矩阵的每一行都加起来得到的向量是为 0 的。

比如说图 $1-2-3$ ，它的拉普拉斯矩阵长这样：

$\begin{vmatrix} 1 & -1 & 0\\ -1 & 2 & -1\\ 0& -1 & 1 \end{vmatrix}$

每一列都单独加起来，得到 $(0,0,0)$ 。

设 $r_i$ 为第 i 行的向量表示，那么我们就有：

$r_1+r_2+r_3=0$

$r_1+r_2=-r_3$

也就是 $r_3$ 能被别的向量通过计算表示，线性相关。

这是一个很重要的点，我们知道方程组中的一个方程如果能被其他方程表示，

那么这个方程就是“没用”的，也就是整个矩阵的秩为 $n-1$ 。

更直接的，线性相关的矩阵的行列式都为 0！

因为有一行（一个方程）是“没用”的，相当于那一行都为 0。

而有一行都为 0 的矩阵的行列式为 0！

也就是原来的拉普拉斯矩阵是“没用”的！

为了让它变得有用，我们考虑去掉它的一行或者一列。

但不能只丢掉一行或者一列，因为柯西—比内公式要求最终乘积结果只能是方阵。

（而且你只求掉一行或者一列的话，那方程组不就多解或者无解了吗？！）

所以就把一列和一行同时丢掉。

再来说关联矩阵为什么要去掉一行。

在拉普拉斯矩阵已经变成 $(n-1)*(n-1)$ 的情况下，

当然是要去掉一行的了。

（不然最后乘出来是 $n*n$ 的矩阵）

还有个原因，关联矩阵也是线性相关的！

不去掉行列式为 0，根本没法算。

（我服了怎么回事你俩）

话又说回来：

把这个 $L[i]=B[i]*B[i]^T$ 代入公式：

$det(AB)=\sum_{S}^{}det(A_s)*det(B_s)$

$det(L[i])$

$=det(B[i]*(B[i])^T)$

$=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)*det(B[i]^T_s)$

$=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

其中求和是对所有从边集 $E$ 中选取 $n-1$ 条边的子集 $S$ 进行的，

$B[i]_S$ 表示 $B[i]$ 中选取 $S$ 对应的列组成的 $(n-1)*(n-1)$ 子矩阵，

$B[i]^T_S$ 表示 $B[i]^T$ 中选取 $S$ 对应的行组成的 $(n-1)*(n-1)$ 子矩阵。

（因为 $B_S$ 是选对应的列，也就是边，所以子集 $S$ 也是选边）

4.生成树与行列式的关系

有了这玩意，才算真正迈上正轨：

$det(L[i])=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

考虑选出来的 $n-1$ 条边构成的图。

我们发现要不就是这样：

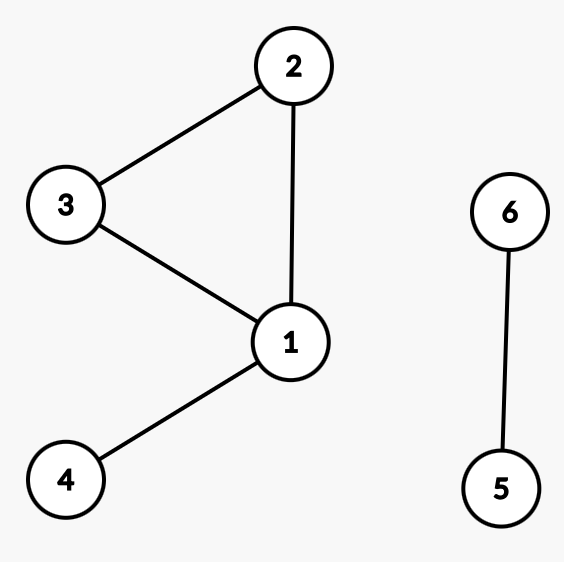
（有环不连通）

要不就是这样：

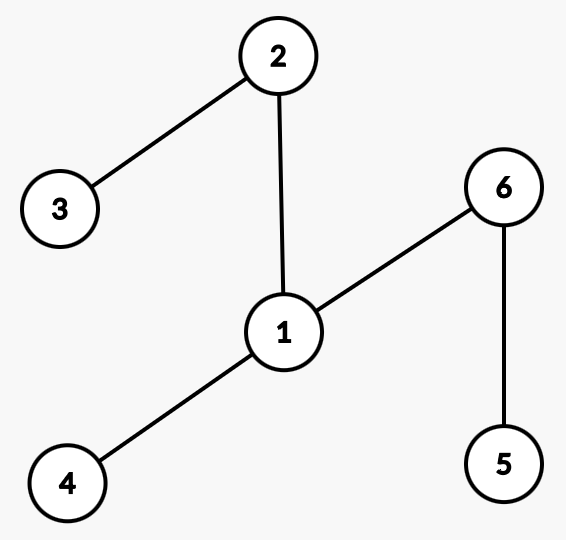
（无环联通/生成树）

同学们可以自己画一下，是不可能出现无环不连通的情况的。

因为你每加一条不成环的边，都会增加一个点，而边数 = 点数 - 1。

同样的，有环连通也不可能出现。

分类讨论下：

（1）有环不连通

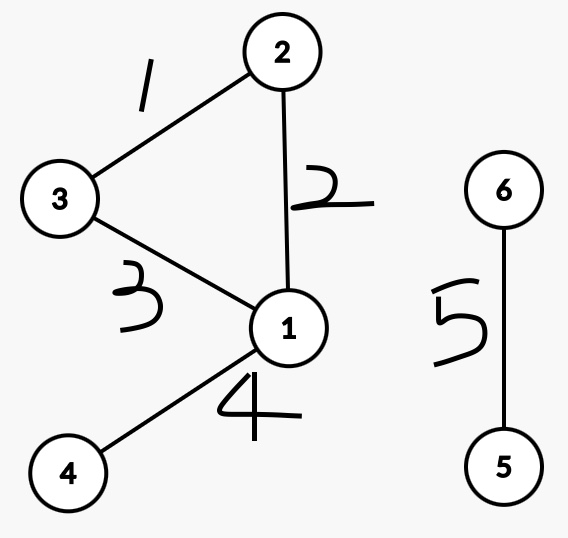
根据上面这张图，构造关联矩阵。

（关于边的方向，我就默认从小连到大，这个不影响）

$B=\begin{vmatrix} 0 & 1 & 1 & 1 &0 \\ 1 & -1 & 0 & 0 & 0\\ -1 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & -1 \end{vmatrix}$

去掉最后一行：

$B[6]=\begin{vmatrix} 0 & 1 & 1 & 1 &0 \\ 1 & -1 & 0 & 0 & 0\\ -1 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 1\end{vmatrix}$

很明显，这个矩阵是线性相关（上面 4 行加起来是 0 向量）的，行列式为 0。

$det(L[i])=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

上面这公式统计的时候，遇到这种有环不连通的图，

行列式都为 0，相当于啥也没发生。

一般性的想一下，如果去掉的一行（点）不在环上。

那环所在的连通块的行（点）一定线性相关。

（环连通块的边连的俩点一个 +1 一个 -1，加起来肯定是 0）

如果去掉的一行（点）在环上，但肯定还有其他连通块。

毕竟一个环要和点数一样的边数，要点数 = 边数 + 1，肯定还有别的连通块没环。

那其他连通块的行（点）一定线性相关。

（和之前理由相同，其实只要有一小块是在去掉点之前就连通的，

并且也没被去掉点，那么那小块的行加起来肯定是 0 向量）

（2）无环连通/生成树

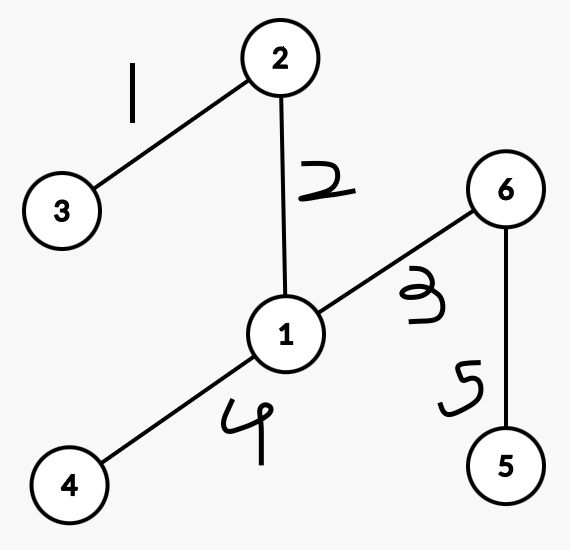
根据上面这张图，构造关联矩阵。

$B=\begin{vmatrix} 0 & 1 & 1 & 1 &0 \\ 1 & -1 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 & -1 \end{vmatrix}$

我们发现，无论去掉哪行，都不可能线性相关。

（虽然去掉一个点，图里还是会有连通块。

但我们去掉的是点，不是边，消失的边对另一点的影响还在。

多出来的影响会导致最终加起来的行向量，对应消失的边的那一维不可能为 0）

$det(L[i])=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

所以在这个求和式里，选出的 $n-1$ 条边只有在无环连通/生成树的情况下，

行列式才不为 0，可以被统计到。

这就是为什么：

啊，矩阵树定理就是给无向连通图建个基尔霍夫矩阵，去掉某一行某一列，

再求个行列式，就是这个图的生成树数量啦！

既然学完了，那就再看看矩阵树定理的官方定义吧：

矩阵—树定理（matrix-tree theorem）：

图的生成树数目等于其基尔霍夫矩阵的任一代数余子式行列式值。

更准确地说，对于一个 n 个点 m 条边的无向图，

其生成树总数为其对应的基尔霍夫矩阵的 n-1 阶余子式（行列式）。

5.代码实现

没学过高斯消元指路这里。

全套基尔霍夫矩阵行列式求生成树数量的代码：

#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 110;
LL K[N][N], ans;
int n, m; void add(int x, int y) {K[x][x]++; K[y][y]++;K[x][y]--; K[y][x]--;
}void gauss() {n--;  // 去掉一行，现在处理(n-1)×(n-1)子矩阵int r = 1; ans = 1;for (int c = 1; c <= n; c++) {for (int i = r + 1; i <= n; i++) {while (K[i][c]) { LL bs = K[r][c] / K[i][c]; for (int j = 1; j <= n; j++) {K[r][j] -= K[i][j] * bs;}swap(K[r], K[i]); ans *= -1; }}if (K[r][c] != 0) {r++;}}// 检查是否满秩（图是否连通）if (r <= n) {cout << 0 << "\n";  // 非连通图，生成树数量为0return;}for (int i = 1; i <= n; i++) {ans *= K[i][i];}cout << abs(ans) << "\n";  // 取绝对值确保非负
}int main() {cin >> n >> m;memset(K, 0, sizeof(K));for (int i = 1; i <= m; i++) {int x, y;cin >> x >> y;if (x != y) {  // 忽略自环（不影响生成树）add(x, y);}}gauss();return 0;
}

查看全文

http://www.dtcms.com/a/359397.html