当前位置：首页 > news >正文

中国剩余定理（以及扩展..）

news 2025/8/29 10:42:23

1.标准中国剩余定理（模数两两互质）

1.1定理

所有模数 m1,m2,⋯,mk两两互质，即：gcd(m $_{i}$ ,m $_{j}$ )=1（ $i\neq j$ ）

即对一个同余方程组

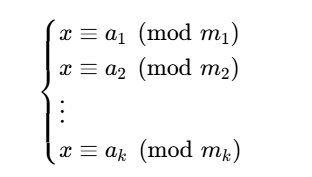
在模 M=m1 m2 ⋯ mk下有唯一解

求解公式：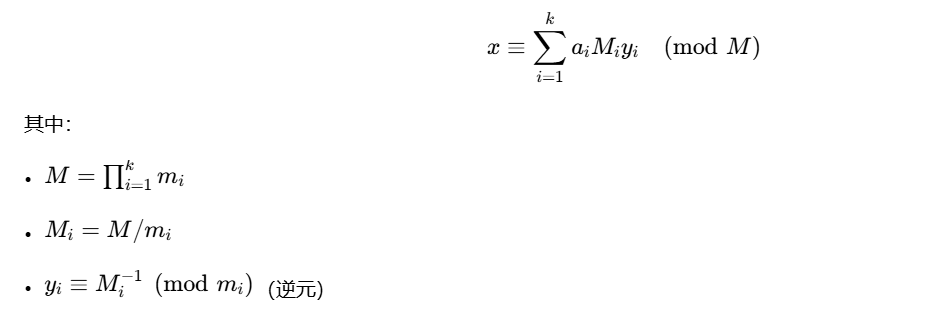

2.脚本

def crt_standard(a, m):"""标准CRT（模数两两互质）"""M = reduce(lambda x, y: x * y, m)result = 0for i in range(len(m)):Mi = M // m[i]inv = pow(Mi, -1, m[i])  # 求逆元result = (result + a[i] * Mi * inv) % Mreturn result

2.扩展中国剩余定理（模数不一定互质）

2.1定理

转（扩展中国剩余定理（ExCRT）-CSDN博客）

2.2脚本

"""扩展欧几里得"""def exgcd(a, b):if 0 == b:return 1, 0, ax, y, q = exgcd(b, a % b)x, y = y, (x - a // b * y)return x, y, q"""扩展中国剩余定理"""def CRT(n, a, m):if n == 1:return a[0], m[0]for i in range(1, n):x, y, d = exgcd(m[0], m[i])if (a[i] - a[0]) % d != 0:return -1, -1t = m[i] // dx = (a[i] - a[0]) // d * x % ta[0] = x * m[0] + a[0]m[0] = m[0] * m[i] // da[0] = (a[0] % m[0] + m[0]) % m[0]return a[0], m[0]# 假设的题目数据（具体根据题目来改变）
n = 8# 同余方程个数
m = [284461942441737992421992210219060544764, 218436209063777179204189567410606431578, 288673438109933649911276214358963643204, 239232622368515797881077917549177081575, 206264514127207567149705234795160750411, 338915547568169045185589241329271490503, 246545359356590592172327146579550739141, 219686182542160835171493232381209438048]# 模数
a = [273520784183505348818648859874365852523, 128223029008039086716133583343107528289, 5111091025406771271167772696866083419, 33462335595116820423587878784664448439, 145377705960376589843356778052388633917, 128158421725856807614557926615949143594, 230664008267846531848877293149791626711, 94549019966480959688919233343793910003]# 余数# 计算所有模数的乘积 p
p = reduce(lambda x, y: x * y, m)# 使用CRT求解基础解和模数
x0, mod = CRT(n, a, m)

查看全文

http://www.dtcms.com/a/355673.html