数据分析学习笔记4：加州房价预测

一、实验概述

        本实验旨在利用机器学习技术，基于加州房价数据集（California Housing Dataset）构建一个房价预测模型。实验涵盖了从数据加载、探索性数据分析（EDA）、数据预处理到模型构建与评估的完整流程。核心任务是利用房屋的各项特征（如收入中位数、房龄、平均房间数等）来预测房价中位数（MEDV）。

二、数据来源

        数据集为机器学习经典数据集：加州房价预测，可以从 sklearn.datasets 直接使用 fetch_california_housing 函数加载。

三、实验过程

1.相关库与初始数据加载

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.linear_model import Ridge
from sklearn.linear_model import ElasticNet
from sklearn.model_selection import GridSearchCV# 加载数据集
california = fetch_california_housing()
data = pd.DataFrame(california.data, columns=california.feature_names)
data['MEDV'] = california.target  # X = data.drop('MEDV', axis=1)
y = data['MEDV']

2.数据探索 (EDA)

        本实验通过简单的统计和可视化对数据进行了初步探索：绘制了特征 (data) 和目标变量 (target) 的分布直方图与特征之间的相关性热力图，并对缺失值进行检测。

#（2）数据探索
#数据缺失值检测
df_X = pd.DataFrame(X, columns=feature_names)
df_y = pd.DataFrame(y, columns=["Target"])
print(df_X.isnull().sum())
print(df_y.isnull().sum())#数据异常值检测
for col in df_X.columns:plt.figure(figsize=(6, 4))sns.boxplot(x=df_X[col])plt.title(f'Boxplot of {col}')plt.show()  #特征的基本统计信息
#print(cleaned_df_X.describe())  
cleaned_df_X = pd.DataFrame(cleaned_df_X, columns=feature_names)  # 将 ndarray 转换为 DataFrame
cleaned_df_y = pd.DataFrame(cleaned_df_y, columns=["Target"])
cleaned_data = pd.concat([cleaned_df_X, cleaned_df_y], axis=1)# 合并特征和目标变量
corr_matrix = cleaned_data.corr()# 计算相关性矩阵
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix,annot=True,     # 显示数值
)
plt.title("特征与目标变量的相关性热力图")
plt.show()

 输出结果如下：

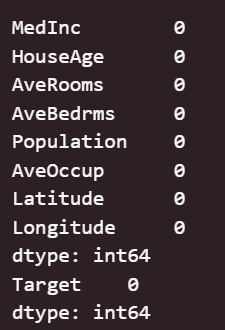
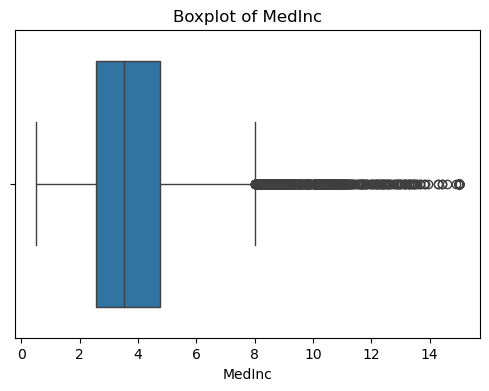
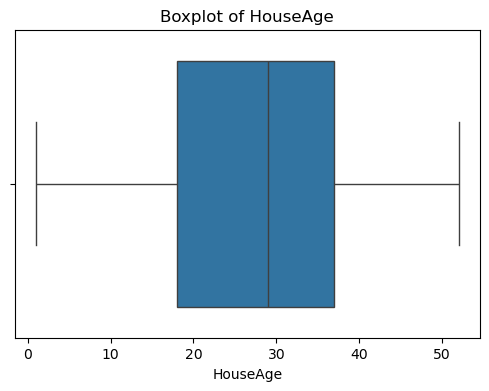
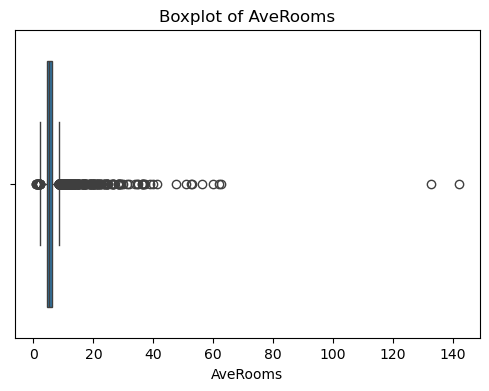
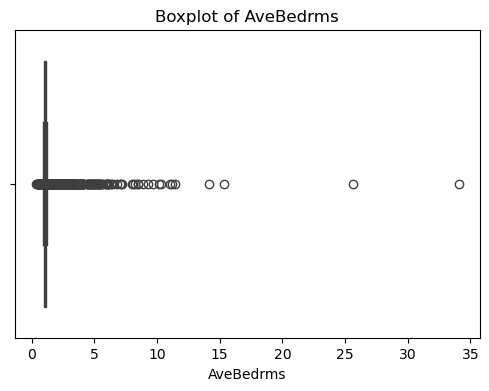
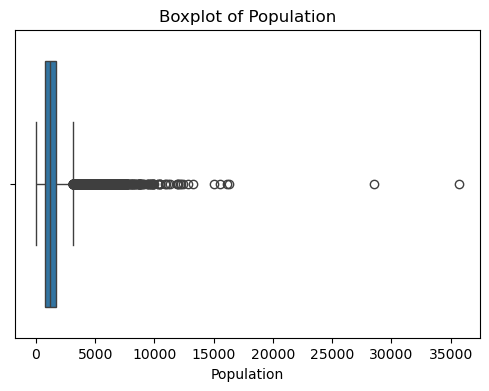
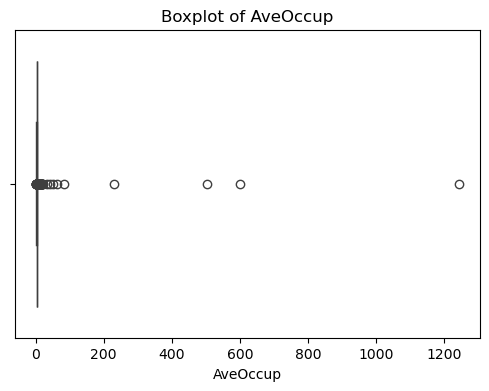
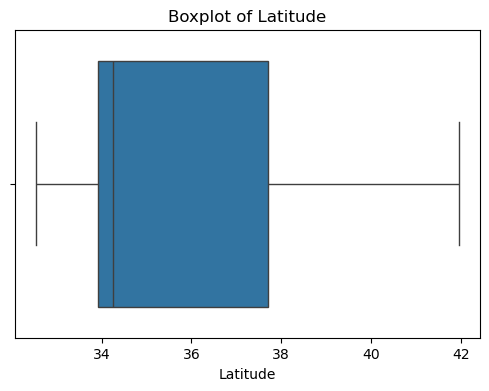
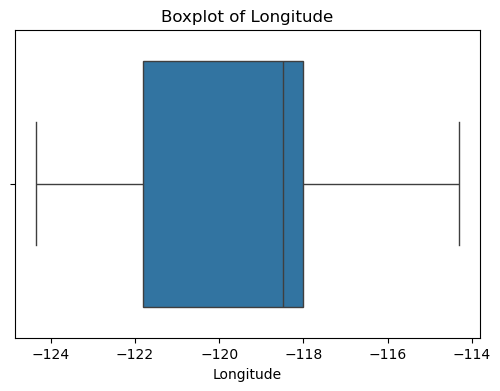
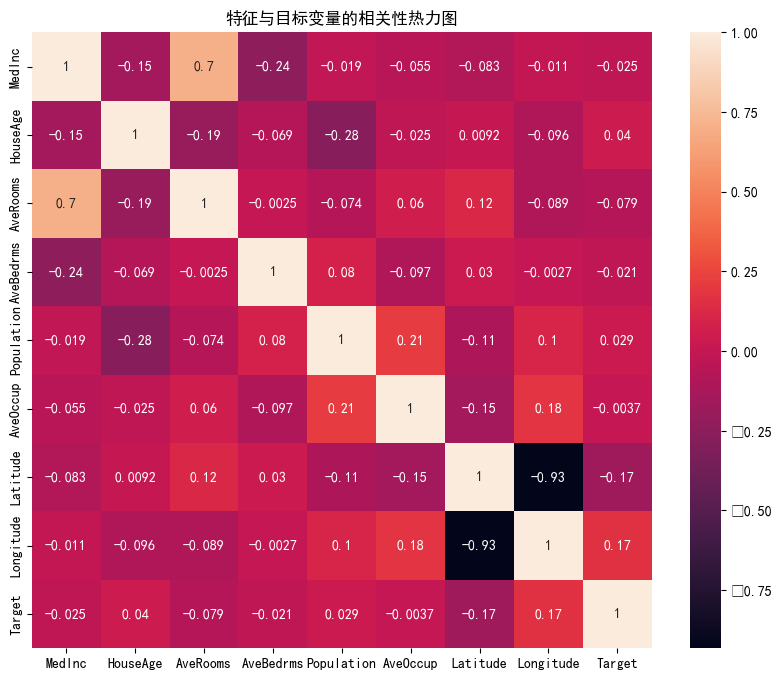
        可以看出，原始数据无缺失值，部分变量异常值样本数量较多，后续需要进行基于Z-score方法的异常值处理。由热力图可知，部分变量的相关性十分明显，如变量 Latitude 与变量 Longitude 具有强负相关性，变量AvgRooms 与变量 Medlnc 具有强正相关性。故拟合模型应采用具有正则化的模型进行。

3. 数据预处理

        主要进行异常值处理、标准化数据、测试训练集的划分的任务。

#(3)数据清洗
z_scores_X = stats.zscore(df_X)
z_scores_y = stats.zscore(df_y)
abs_z_scores_X = np.abs(z_scores_X)
abs_z_scores_y = np.abs(z_scores_y)  #处理异常值
def remove_outliers_iqr(df, factor=1.5):df_cleaned = df.copy()for col in df.columns:Q1 = df[col].quantile(0.25)Q3 = df[col].quantile(0.75)IQR = Q3 - Q1lower_bound = Q1 - factor * IQRupper_bound = Q3 + factor * IQRdf_cleaned = df_cleaned[(df_cleaned[col] >= lower_bound) & (df_cleaned[col] <= upper_bound)]return df_cleanedcleaned_df_X = remove_outliers_iqr(df_X)
cleaned_df_y = y[cleaned_df_X.index]
print("原始样本数量:", len(df_X))
print("清洗后样本数量:", len(cleaned_df_X))# 标准化 X
scaler = StandardScaler()
X_scaled = scaler.fit_transform(cleaned_df_X)
y_scaled = cleaned_df_y# 按照 80% 训练集，20% 测试集划分
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, test_size=0.2, random_state=7)print("训练集特征维度:", X_train.shape)
print("测试集特征维度:", X_test.shape)
print("训练集目标维度:", y_train.shape)
print("测试集目标维度:", y_test.shape)

输出结果如下：

        可以看出，进行基于Z-score方法的异常值处理之后，样本数量由20940下降至16842，为后续模型构建的准确性打下基础。

4. 模型构建

        本实验采用线性回归、LASSO回归、岭回归、弹性网回归4类方法进行模型的构建，并以均方误差 (Mean Squared Error, MSE)与决定系数 (R² Score)作为模型的评估指标，最终选取效果最优的模型作为最终应用模型。

#（5）线性回归
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
LR = LinearRegression()
LR.fit(X_train,y_train)
# 预测
y_pred_linear = LR.predict(X_test)#评价
# 模型评估
print("Linear Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_linear))
print("R^2 Score:", r2_score(y_test,y_pred_linear))#(6) LASSO 回归（带 L1 正则化）
from sklearn.linear_model import Lassolasso = Lasso(alpha=0.3, max_iter=10000)
lasso.fit(X_train, y_train)# 预测
y_pred_lasso = lasso.predict(X_test)# 模型评估
print("LASSO Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_lasso))
print("R^2 Score:", r2_score(y_test, y_pred_lasso))
print("Coefficients:", lasso.coef_)#(7) 岭回归（带 L2 正则化）
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0, max_iter=10000)
ridge.fit(X_train, y_train)# 预测
y_pred_ridge = ridge.predict(X_test)# 模型评估
print("Ridge Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_ridge))
print("R^2 Score:", r2_score(y_test, y_pred_ridge))
print("Coefficients:", ridge.coef_)#(8) 弹性网回归（L1 + L2 正则化）
from sklearn.linear_model import ElasticNetelastic_net = ElasticNet(alpha=1.0, l1_ratio=0.2, max_iter=10000)
elastic_net.fit(X_train, y_train)
# 预测
y_pred_elastic = elastic_net.predict(X_test)# 模型评估
print("Elastic Net Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_elastic))
print("R^2 Score:", r2_score(y_test, y_pred_elastic))
print("Coefficients:", elastic_net.coef_)

输出结果如下：

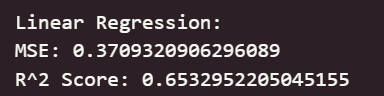
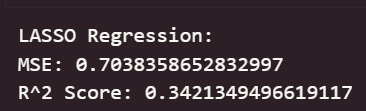
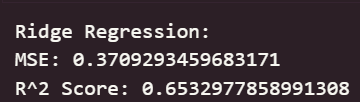
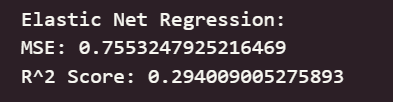
        可以看出，在初始为调参的情况下，线性回归模型与岭回归模型在测试集上取得了最佳的预测性能（最低的 RMSE 和最高的 R² Score），这表明集成学习方法能够有效学习加州房价数据中的复杂模式和特征交互。

5.模型参数调优（可视化对比）

由于线性回归模型与岭回归参数较少，初始模型已是最优模型，故对LASSO回归模型与弹性网模型进行参数调优。

#（9）lasso、弹性网模型参数调优
# 1、LASSO 模型
from sklearn.model_selection import GridSearchCVparam_grid_lasso = {'alpha': [0.001, 0.01, 0.1, 1.0, 10.0]}# LASSO 回归参数范围
lasso = Lasso(max_iter=10000)# 网格搜索
grid_lasso = GridSearchCV(lasso, param_grid_lasso, scoring='neg_mean_squared_error', cv=5)
grid_lasso.fit(X_train, y_train)# 最佳参数和最佳模型
best_lasso = grid_lasso.best_estimator_
y_pred_lasso_best = best_lasso.predict(X_test)print("LASSO - Best params:", grid_lasso.best_params_)
print("MSE after tuning:", mean_squared_error(y_test, y_pred_lasso_best))
print("R^2 Score after tuning:", r2_score(y_test, y_pred_lasso_best))# 2、ElasticNet 模型
param_grid_elastic = {'alpha': [0.001, 0.01, 0.1, 1.0, 10.0],'l1_ratio': [0.1, 0.3, 0.5, 0.7, 0.9]
}#ElasticNet 参数范围elastic_net = ElasticNet(max_iter=10000)# 网格搜索
grid_elastic = GridSearchCV(elastic_net, param_grid_elastic, scoring='neg_mean_squared_error', cv=5)
grid_elastic.fit(X_train, y_train)# 最佳模型
best_elastic = grid_elastic.best_estimator_
y_pred_elastic_best = best_elastic.predict(X_test)print("ElasticNet - Best params:", grid_elastic.best_params_)
print("MSE after tuning:", mean_squared_error(y_test, y_pred_elastic_best))
print("R^2 Score after tuning:", r2_score(y_test, y_pred_elastic_best))plt.figure(figsize=(10, 10))# 调参前 LASSO
plt.subplot(2, 2, 1)
plt.scatter(y_test, y_pred_lasso, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('LASSO (Before Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')# 调参后 LASSO
plt.subplot(2, 2, 2)
plt.scatter(y_test, y_pred_lasso_best, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('LASSO (After Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')# 调参前 ElasticNet
plt.subplot(2, 2, 3)
plt.scatter(y_test, y_pred_elastic, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('ElasticNet (Before Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')# 调参后 ElasticNet
plt.subplot(2, 2, 4)
plt.scatter(y_test, y_pred_elastic_best, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('ElasticNet (After Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')plt.tight_layout()
plt.show()

输出结果如下：

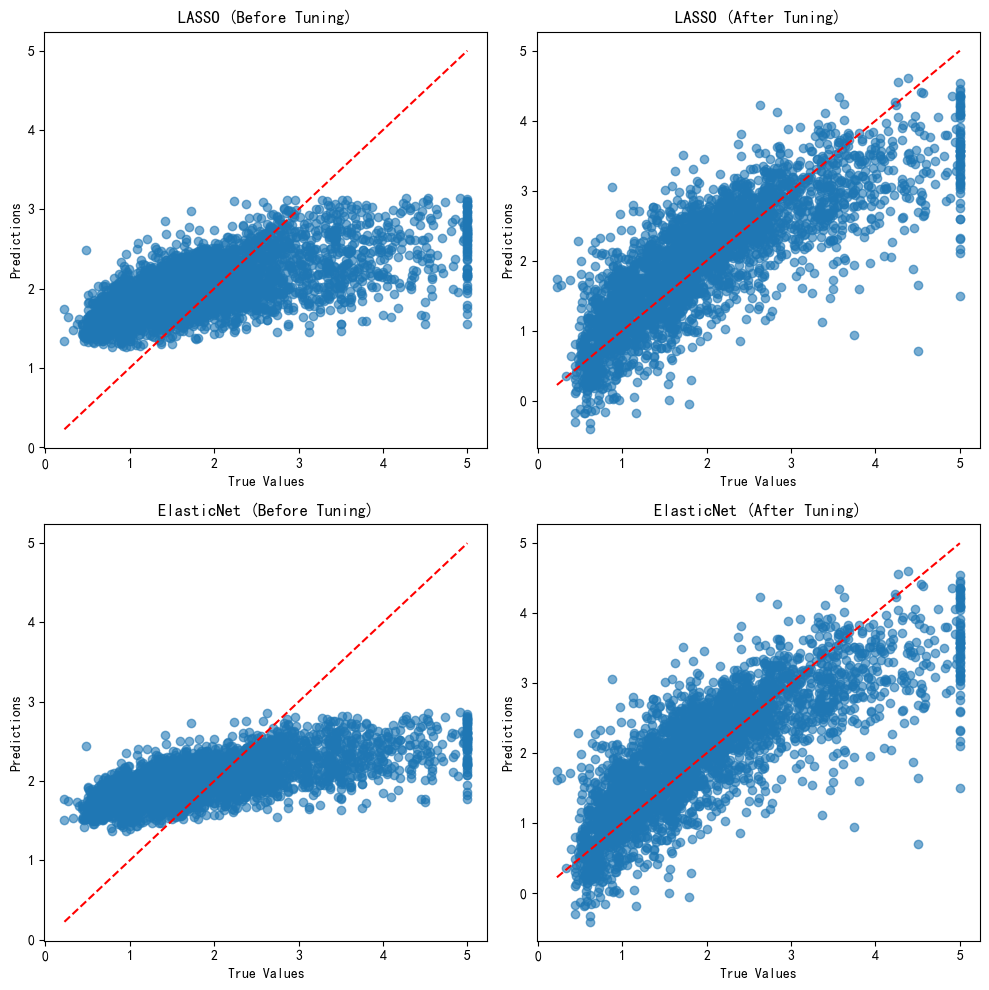
        可以看出，相对初始模型，参数调优后的LASSO模型与弹性网模型在测试集的评价大幅上升，效果与线性回归和岭回归相差无几。

四、 结论

        本实验成功完成了加州房价预测的任务。通过数据加载、清洗、探索性分析和特征工程，为模型训练准备了高质量的数据。通过尝试不同的回归模型，发现选择的4类模型在该数据集上表现相差无几，都可以相对准确地预测房价中位数。

改进方向:

1. 进一步的特征工程: 可以尝试创建特征之间的交互项或多项式特征，或许能进一步提升模型性能。

2. 尝试其他模型: 可以尝试使用梯度提升树（如 XGBoost, LightGBM）等更强大的集成模型。

3. 深入分析误差: 分析预测误差较大的样本点，找出这些样本的共同特征，有助于理解模型的局限性并指导下一步的优化。