少样本图异常检测系列【A Survey of Few-Shot Graph Anomaly Detection】

文献列表：

1. DAGAD: Data Augmentation for Graph Anomaly Detection 2022年10月 ICDM开源
2. Cross-Domain Graph Anomaly Detection via Anomaly-aware Contrastive Alignment 2022年12月 AAAI开源
3. Cross-Domain Graph Level Anomaly Detection 2024年12月 TKDE开源
4. Class Label-aware Graph Anomaly Detection 2023年8月 CIKM开源
5. Truncated Affinity Maximization: One-class Homophily Modeling for Graph Anomaly Detection 2024年 NIPS开源
6. PREM: A Simple Yet Effective Approach for Node-Level Graph Anomaly Detection 2023年10月 ICDM开源
7. ARC: A Generalist Graph Anomaly Detector with In-Context Learning 2024年 NIPS开源
8. Zero-shot Generalist Graph Anomaly Detection with Unified Neighborhood Prompts 2025年 IJCAI开源
9. SpaceGNN: Multi-Space Graph Neural Network for Node Anomaly Detection with Extremely Limited Labels 2025年 ICLR开源
10. AnomalyGFM: Graph Foundation Model for Zero/Few-shot Anomaly Detection 2025年 KDD开源
11. AffinityTune: A Prompt-Tuning Framework for Few-Shot Anomaly Detection on Graphs 2025年 KDD开源
    标记星号的是与主题契合度高的论文

DAGAD_2022

核心目标：DAGAD旨在解决图异常检测中的异常样本稀缺和类别不平衡问题。
设计思路：基于随机置换的数据增强技术扩充异常样本，结合类别感知的损失函数优化决策边界。

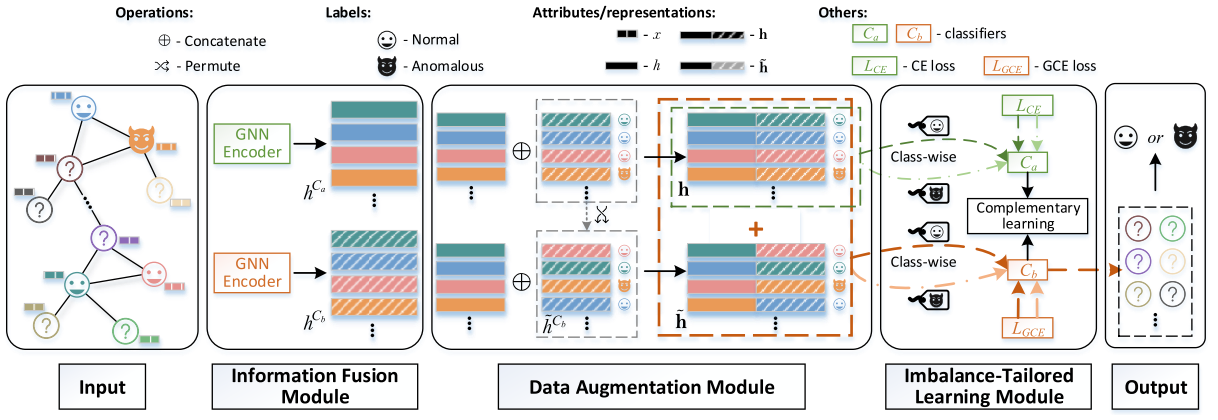
整体流程：
（1）信息融合模块：双GNN编码器融合图拓扑与节点属性，生成低维表示。
（2）数据增强模块：对低维表示中的节点向量进行随机置换，通过双路径拼接生成样本。
（3）不平衡学习模块：类感知损失函数训练双分类器，两个分类器分别专注于学习异常类特征和泛化决策边界。

ACT_2022

核心挑战：
（1）异常分布未知且多变：目标图中的异常类型可能和源图完全不同，无法假设它们的分布相似。
（2）图结构和属性差异大：源图和目标图在拓扑结构（如节点度分布）、属性空间（如特征维度）上可能存在巨大差异，导致传统的域适应方法失效。
核心目标：利用一个有标签的源图中的异常知识，来帮助检测一个无标签的目标图中的异常。
设计思路：考虑到异常分布未知且多变，专注于学习和对齐正常类的表示（one-class alignment），并利用已知的异常标签来学习一个更鲁棒的正常类表示，然后将这个正常的知识迁移到目标图。

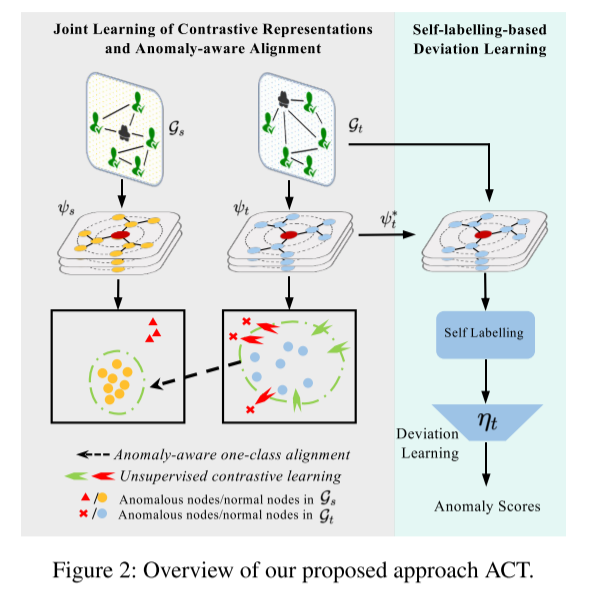
整体流程：
（1）联合学习阶段

• 无监督对比学习：在目标图$G_t$上进行，目的是学习节点的正常表示。
• 异常感知的单类对齐：将目标图$G_t$的节点表示与源图$G_s$的正常节点表示对齐，同时利用源图的异常标签信息来增强对正常类的理解。
• 该阶段输出一个经过域适应的、用于GAD的节点表示映射${\psi }_t^{\ast }$。

（2）自标记偏差学习

• 在第一阶段得到的表示空间${\psi }_t^{\ast }$上，使用一个现成的异常检测器来识别伪异常。
• 利用这些伪标签，重新学习一个针对目标图的异常打分网络${\eta }_t$。
• 最终，使用${\eta }_t$和${\psi }_t^{\ast }$对目标图进行异常检测。

ARMET*_2024

核心挑战：
（1）源域标签不完整：通过一类分类器，仅利用源域的正常图学习正常模式。
（2）域差异大：通过参数共享的特征提取器和对抗性的域分类器（基于对抗学习的度量），实现源域和目标域特征分布的对齐。
（3）类别判别性弱：通过类别对齐器，利用伪标签进一步强化正常和异常类别的分离，提升模型的判别能力。
核心目标：根据域适应理论的误差上界公式，要最小化目标域的误差，需要同时最小化源域误差（确保模型能在源域上很好地学习）、最小化域差异（让源域和目标域的特征表示尽可能相似）、最小化理想联合分类器误差（确保两个域的正常模式能被统一识别）。
设计思路：在学习域不变表示的同时，保持并增强其类判别性，有效地将在源域学到的正常知识迁移到目标域，从而在目标域上准确地检测出异常图。

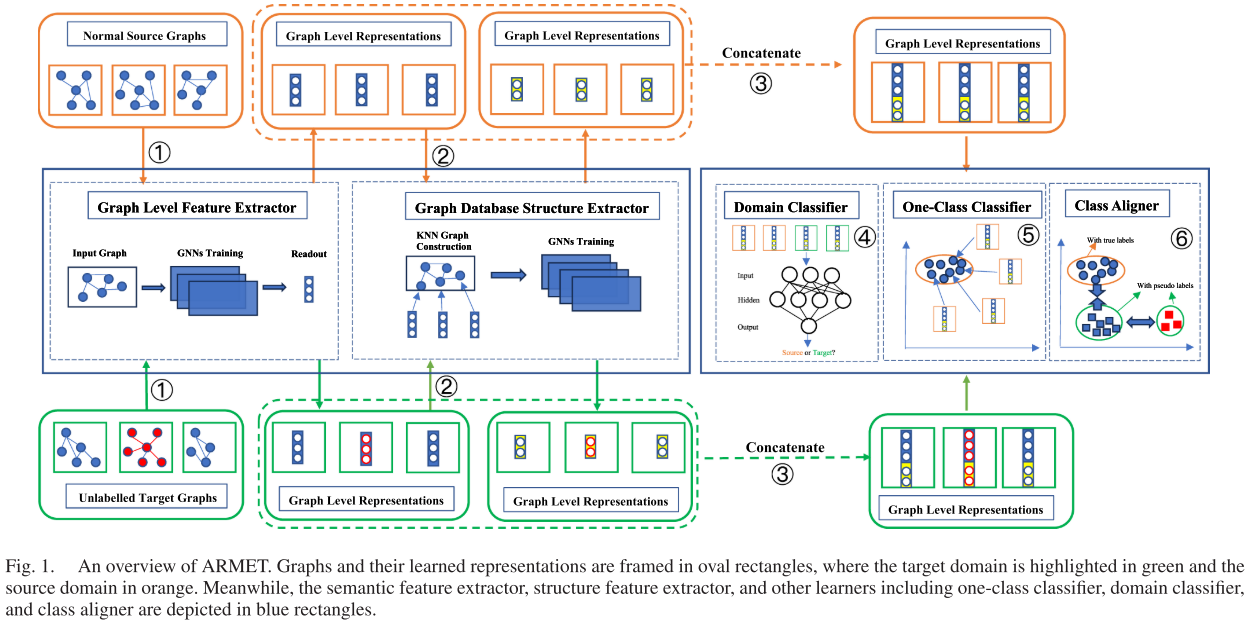
整体流程：
（1）图特征提取模块

• 参数共享的特征提取器：包含一个语义特征提取器和一个结构特征提取器，分别捕捉图的节点/边属性信息和拓扑结构信息。同一个特征提取器被用于处理源域和目标域的所有图，在实现域对齐的前提下，确保了不同域的图被映射到同一个表示空间中进行比较。

（2）跨域异常检测模块

• 一类分类器：学习一个超球体，目标是将源域正常图的表示都包含在这个球体内，而将异常图的表示排除在外，训练完成后，这个分类器可以直接用于对目标域图的表示进行打分。
• 域分类器：实现对抗学习中的对抗部分，用于最小化域差异，它是一个二分类器，试图判断输入的表示是来自源域还是目标域。在对抗学习度量中，特征提取器的目标是生成能让域分类器“困惑”的表示，即让域分类器无法准确区分源域和目标域。
• 类别对齐器：旨在直接最小化理想联合分类器的误差，使用在源域上训练好的一类分类器，对目标域图的表示进行打分，从而生成伪标签（得分高的可能是正常，得分低的可能是异常）。从而让源域的正常图和目标域的伪正常图的表示尽可能接近，让目标域的伪正常图和伪异常图的表示尽可能远离。

这两个模块联合训练，整个框架是端到端的，这意味着在每次迭代中，所有组件的参数会根据总损失一起更新。

CLAD*_2023

核心思想：传统的无监督GAD方法完全忽略类标签信息，结构异常（Structural Anomalies）往往会破坏图的同质性，即一个节点与其邻居属于不同类。因此，类标签信息（或其预测分布）是检测结构异常的宝贵线索。然而，在真实场景中，只有一小部分节点的类标签是已知的。
设计思路：利用有限的类标签信息来增强无监督异常检测性能的框架。

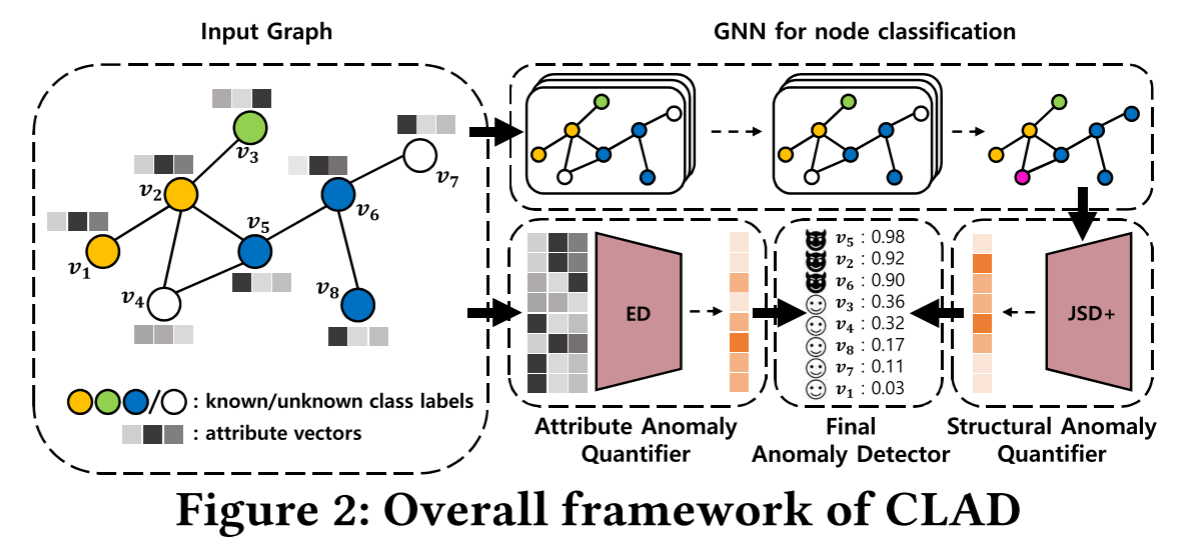
整体流程：
步骤一：半监督节点分类器训练
为图中的每一个节点（无论其标签是否已知）生成一个类别概率分布$p_i$向量，这个分布反映了模型对节点所属类别的置信度。对于有真实标签的节点，使用标准的交叉熵损失进行监督学习。对于没有真实标签的节点，可以使用伪标签，伪标签是通过在节点属性上运行简单的聚类算法得到的。
步骤二：双模块异常量化
（1）结构异常量化器
结构异常节点通常与其邻居在类别分布上存在显著差异，一个节点的类别分布与其邻居的类别分布越不一致，它就越可能是结构异常。度量结构异常的方法是Jensen-Shannon散度（JSD），JSD是衡量一组概率的发散度的度量，其定义为：
$$\begin{array}{l}p\_av{g}_i=\frac{1}{|\mathcal{N}(i)|}{\sum }_{j\in \mathcal{N}(i)}^{}{p}_j\\ JSD(i)=H(p\_av{g}_i)-\frac{1}{|\mathcal{N}(i)|}{\sum }_{j\in \mathcal{N}(i)}^{}H(p_j)\end{array}$$
$H(p)$是Shannon熵，$H(p\_avg(i))$是平均分布的熵，$\frac{1}{|\mathcal{N}(i)|}{\sum }_{j\in \mathcal{N}(i)}^{}H(p_j)$是邻居分布熵的平均值。$H(p\_avg(i))$高意味着邻居的平均类别分布是不确定的、分散的，即邻居来自多个不同类别，$\frac{1}{|\mathcal{N}(i)|}{\sum }_{j\in \mathcal{N}(i)}^{}H(p_j)$低意味着每个邻居自身的类别分布是确定的、集中的，即每个邻居都明确属于某个类别，当$H(p\_avg(i))$高而$\frac{1}{|\mathcal{N}(i)|}{\sum }_{j\in \mathcal{N}(i)}^{}H(p_j)$低时意味着邻居们各自属于明确的类别，但它们的平均分布却很分散，说明$v_i$连接了不同类别的群体。
然而，原始JSD对低度节点更敏感，对高度节点不敏感，为此，$JSD2(i)=JSD(i)\ast log(degre{e}_i)$通过乘以节点度的对数，平衡了不同度节点的分数。尽管JSD2缓解了分数差异的问题，但它遇到了一个关于分数实际价值的新问题。具体地，通过将节点度乘以JSD值，我们有可能获得高度节点的极大值，而不管它们的异常情况。如果良性节点的节点度较高，则JSD2会将其预测为异常。对于高度良性的节点，可以使用不会变得很大的值来处理此问题，据实验观察，预测为良性节点的相邻节点可能与良性节点本身共享相同类别标签。因此，定义其预测类别与节点$v_i$相同的相邻节点数为KaTeX parse error: Undefined control sequence: \math at position 21: …a_i=\sum_{j\in \̲m̲a̲t̲h̲ ̲N(i)}^{}(argmax…，良性节点$degre{e}_i-{\gamma }_i$的值往往较小，结构异常的值较大。利用该值，定义$JSD+(i)=JSD(i)\cdot log(degre{e}_i-{\gamma }_i)$，JSD+通过对良性节点的节点度赋予较低的权重来解决上述问题。
（2）属性异常量化器
属性异常节点的属性与其邻居的属性显著不同，度量方法为欧式距离：
$$ED(i)=||x_i-x\_av{g}_i|{|}_2$$
（3）最终异常分数融合
综合结构和属性两个维度的信息，得到一个全面的异常评分：
$$y_i=\alpha \ast s_i+(1-\alpha )\ast a_i$$

TAM*_2023

核心思想：受单类同质现象的启发，引入了一种基于局部节点亲和度的异常评分度量。正常节点倾向于与相似的节点（无论是属性还是结构上）连接，表现出强的局部亲和性（Local Affinity），而异常节点则与周围环境格格不入，表现出弱的局部亲和性。TAM的核心思想是学习一个能够最大化局部亲和性的节点表示空间。在这个空间中，正常节点会因其高亲和性而被“拉近”，而异常节点因其低亲和性被“推开”或“孤立”。

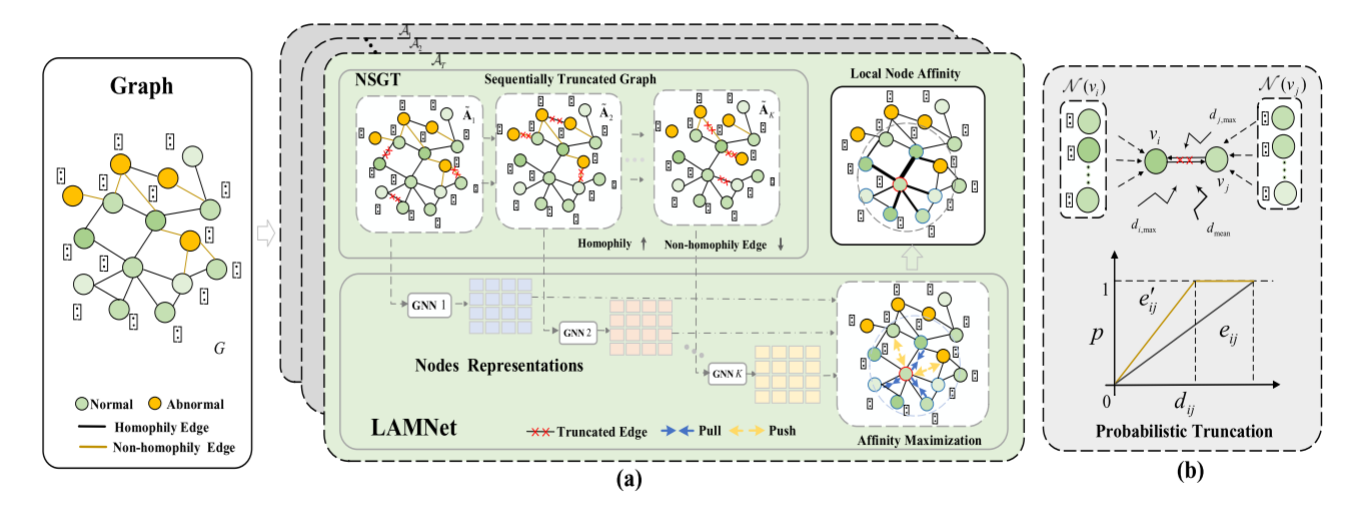
整体流程：TAM由两个组成部分构成，即基于局部亲和力最大化的图神经网络（LAMNet）和保持正常结构的图截断（NSGT）。LAMNet在由NSGT产生的迭代截断的图结构上使用局部亲和力最大化目标来训练图神经网络。
局部亲和度可以定义为与相邻节点的平均相似度，并且异常分数$f$与亲和度相反：
$$h(v_i)=\frac{1}{|\mathcal{N}(v_i)|}\sum _{v_j\in \mathcal{N}(v_i)}sim({\mathrm{x}}_i,{\mathrm{x}}_j);f(v_i)=-h(v_i)$$
本地节点亲和性在原始节点属性空间中可能不能很好地工作，因为：

• 原始数据空间中可能存在许多不相关的属性；
• 一些异常节点也可以连接到相似属性的节点。

为了解决这个问题，TAM建议学习最优节点表示，以最大化与邻居具有较强同质关系的节点在节点属性方面的局部亲和力。由于图中存在大量正常节点，基于TAM学习到的节点表示空间针对正常节点进行了优化，使得正常节点比异常节点具有更强的局部亲和力。基于TAM的局部异常节点亲和度异常评分可以定义为：
$$f_{TAM}(v_i;\Theta ,\mathrm{A},\mathrm{X})=\frac{1}{|\mathcal{N}(v_i)|}\sum _{v_j\in \mathcal{N}(v_i)}sim({\mathrm{h}}_i,{\mathrm{h}}_j)$$
其中，${\mathrm{h}}_i=\psi (v_i;\Theta ,\mathrm{A},\mathrm{X})$是通过映射函数$\psi$学习的节点$v_i$的基于GNN的节点表示。
组件一：Local Affinity Maximization Networks (LAMNet)
LAMNet的目标是学习一种基于GNN的映射函数$\psi$，该函数最大化具有同质关系的节点与其邻居之间的亲和力，同时保持具有非同质关系的节点的亲和力较弱。具体地说，从图节点到使用$l$GNN层的新表示的投影可以写为：
$${\mathrm{H}}^{(l)}=GNN(\mathrm{A},{\mathrm{H}}^{(l-1)};{\mathrm{W}}^{(l)})$$
组件二：Normal Structure-preserved Graph Truncation（NSGT）
LAMNet是由单类同质性（one-class homophily property）驱动的，但其目标和图卷积运算可能会受到非同质边（即连接正常和异常节点的边）存在的影响。NSGT组件旨在移除这些非同质边，从而产生具有基于同质边的正常图结构的截断邻接矩阵$\tilde{A}$。然后，使用截断邻接矩阵$\tilde{A}$而不是原始邻接矩阵$A$来执行LAMNet。
由于同质边（连接正常节点的边）连接相似属性的节点，所以同质边的节点之间的距离通常比非同质边的节点之间的距离小得多，但也可能存在连接不相似的正常节点的同质边。受此启发，NSGT采取了一种概率方法，并按照如下方式执行图截断，对于一个给定边$e_{ij}=1$，当且仅当节点$v_i$和$v_j$之间的距离足够大，或者$e_{ij}=0$时，它就被认为是一条非同质边：
$$e_{ij}\leftarrow 0iff{d}_{ij}>r_i\&d_{ij}>r_j,\forall e_{ij}=1$$
其中，$d_{ij}$是节点$v_i$和节点$v_j$之间基于节点属性的欧氏距离，$r_i$是从区间$[d_{mean},d_{i,max}]$中随机选取的值，其中$d_{mean}=\frac{1}{m}{\sum }_{(v_i,v_j)\in \epsilon }^{}{d}_{ij}$表示图的平均距离，其中$m$是邻接矩阵中非零元素的个数，$d_{i,max}$是{dik,vk∈N(vi)}\{d_{ik},v_k\in \mathcal N(v_i)\}{dik​,vk​∈N(vi​)}中的最大距离，$r_j$同理。理论上，$r_i<d_{ij}$的概率可以被定义为：
$$p(r_i<d_{ij})=\frac{max(d_{ij}-d_{mean},0)}{d_{ij}-d_{mean}}$$
则$e_{ij}$在截断期间被移除的概率是：
$$p(\epsilon \setminus e_{ij})=p(r_i<d_{ij})p(r_j<d_{ij})$$
考虑到每个节点的$[d_{mean},d_{i,max}]$的巨大差异以及截断的随机性，NSGT执行顺序迭代截断而不是单遍截断。在每次迭代中，它以与其关联节点之间的距离成正比的概率随机移除一些不同的边，然后它更新具有被移除边的节点的范围$[d_{mean},d_{i,max}]$。因此，对于图$G$上的$K$次迭代，它将产生一组$K$个顺序截断的图，其对应的截断邻接矩阵$\mathcal{A}=\widetilde{{\mathcal{A}}_1},\widetilde{{\mathcal{A}}_2},...,\widetilde{{\mathcal{A}}_K}$。由于图是按照顺序截断的，因此有${\epsilon }_{i+1}\subset {\epsilon }_i$，其中，${\epsilon }_i$表示第$i$次迭代后留下的边集。

PREM*_2023

核心目标：通过一个极其简洁的两阶段框架——预处理和匹配，将复杂的图神经网络消息传递过程与模型训练解耦。
设计思路：将图结构聚合与异常性判断彻底分离，用最简单的相似度计算替代复杂的GNN消息传递和重构任务。预处理只做一次，训练过程无需昂贵的图操作，实现了数量级的效率提升。

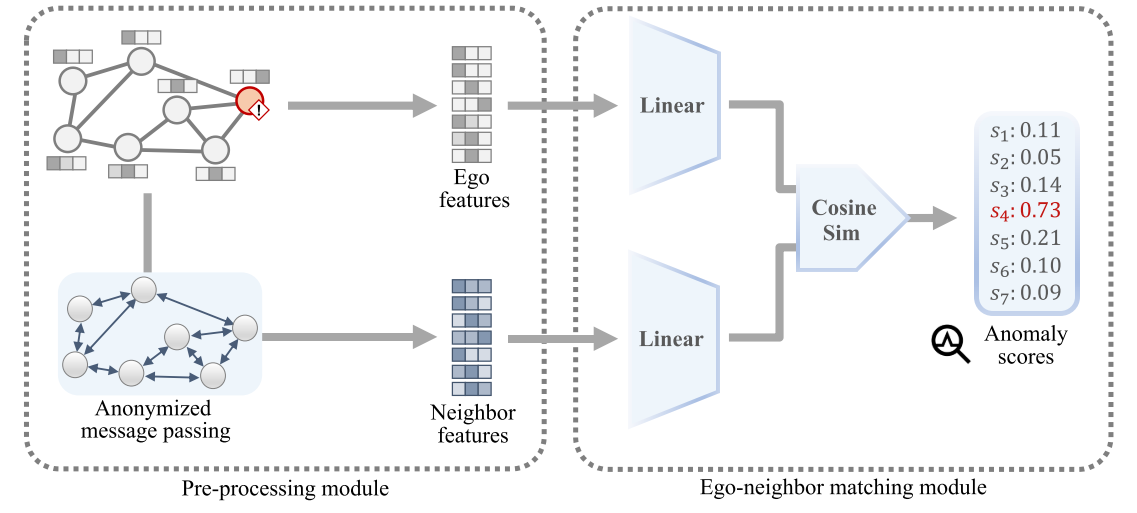
整体流程：
（1）预处理模块
旨在生成一个能捕捉多跳邻居信息的邻接矩阵$A^k$，$A^k$将$k$跳邻居的信息融入了节点的表示中，具体操作是进行$k$步的均值传播，$A^k$可以看作是${\hat{A}}^k$经过行归一化后的结果，${\hat{A}}^k$的$(i,j)$元素表示节点$i$和$j$之间长度为$k$的路径数量，经过归一化后$A^k$的每一行$A_i^k$可以被解释为节点$i$对其$k$跳邻居的注意力权重。
（2）匹配模块
异常节点通常与其邻居在特征上不一致，计算每个节点$v_i$的自身特征$x_i$与其邻居聚合特征$n_i$之间的匹配度，匹配度越低，节点越异常。PREM的目标是最大化正常节点的匹配分数，最小化异常节点的匹配分数。

ARC*_2024

核心目标：在多个不同领域的训练数据集上训练一个单一模型，当面对一个全新的、未见过的测试数据集时，模型能够直接进行异常检测，无需任何重新训练或微调，其遵循正常少样本设置，即，在推理时，对于测试数据集，只提供极少数已知的正常节点标签。模型必须利用这些上下文来推断其余节点的异常性。
设计思路：利用上下文学习来实现无需微调的跨图迁移。

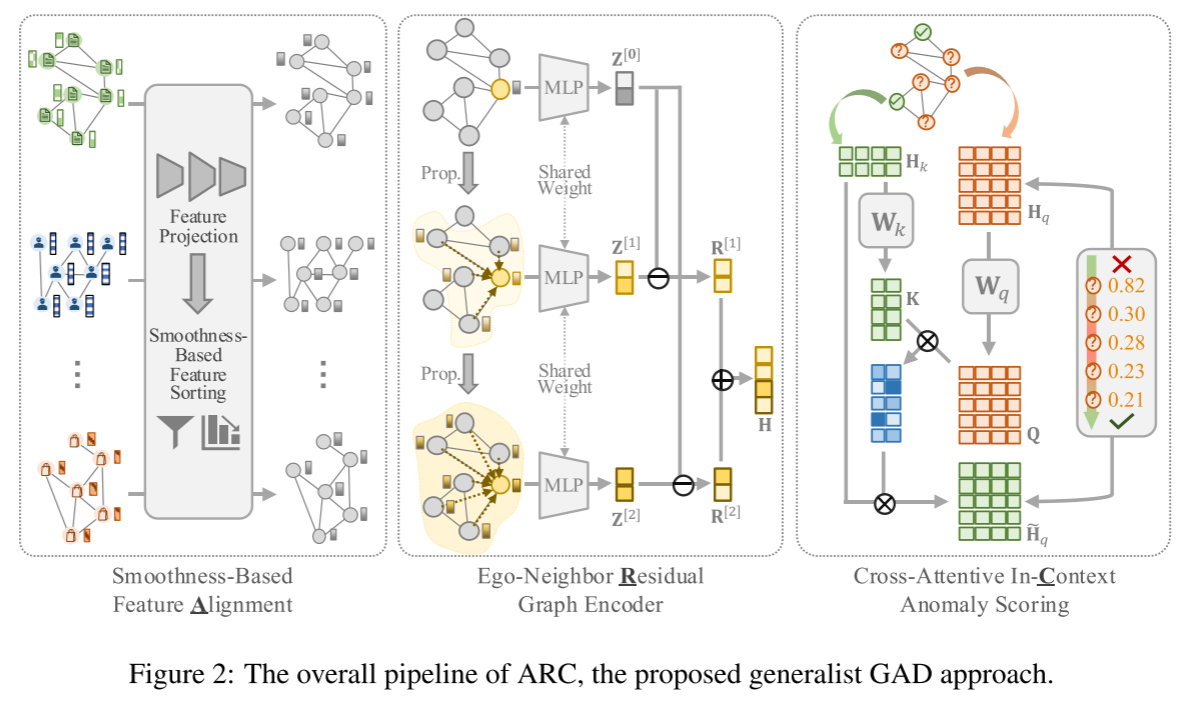
整体流程：
ARC由三个模块组成：
模块一：平滑性特征对齐
不同图的节点特征千差万别（维度不同、语义不同），直接训练一个通用模型是不可能的。ARC提出了一个两阶段的特征对齐模块，将所有图的特征映射到一个公共的、异常敏感的特征空间。
（1）特征投影
使用一个可学习的线性变换将所有图的原始特征投影到一个预定义的公共维度。
（2）基于平滑性的特征排序
不仅要统一维度，还要让特征维度的顺序具有意义，使其对异常敏感。利用图信号处理中的“平滑性”概念，即一个特征在图上越平滑，意味着相邻节点在该特征上的值越相似，正常节点通常表现出高平滑性，异常节点往往在某些特征上与其邻居差异巨大，导致这些特征的平滑性低。
对于投影后的$d$维特征中的每一维$j$，计算其在图$G$上的平滑性得分$s_k$：
$$s_k(\mathrm{X})=-\frac{1}{|E|}\sum _{(v_i,v_j)\in E}({\mathrm{X}}_{ik}-{\mathrm{X}}_{jk})$$
${\mathrm{X}}_{ik}$是节点$i$在第$k$维的值，$s_k$越小，表示该维度的特征在图上越平滑。
将$d$个特征维度按照其平滑性得分从小到大排序，排序后，特征矩阵的第一列对应的是图上最平滑的特征，最后一列对应的是最不平滑的特征。
模块二：自我-邻居残差图编码器
不直接学习节点的绝对表示，编码器采用残差计算，能够捕捉每个节点的多跳亲和力模式，图编码器包括三个步骤：多跳传播、基于共享MLP的变换和自邻残差操作。在前两步中，对$L$次迭代的对齐特征矩阵${\mathrm{X}}^{\prime }={\mathrm{X}}^{[0]}$进行传播，然后用共享的MLP网络对初始特征和传播特征进行变换：
$${\mathrm{X}}^{[\mathrm{l}]}=\tilde{A}{\mathrm{X}}^{[\mathrm{l}-1]},{\mathrm{Z}}^{[\mathrm{l}]}=MLP({\mathrm{X}}^{[\mathrm{l}]})$$
与大多数GNN只考虑$L$次迭代传播后的特征/表示不同，ARC将初始特征和中间传播特征结合在一起，并将它们转换到相同的表示空间中。在得到${\mathrm{Z}}^{[0]},...,{\mathrm{Z}}^{[\mathrm{L}]}$之后，取${\mathrm{Z}}^{[\mathrm{l}]}(1\le l\le L)$与${\mathrm{Z}}^{[0]}$之差计算残差表示，再将多跳残差表示拼接形成最终嵌入：
$${\mathrm{R}}^{[\mathrm{l}]}={\mathrm{Z}}^{[\mathrm{l}]}-{\mathrm{Z}}^{[0]},\mathrm{H}=[{\mathrm{R}}^{[1]}||...||{\mathrm{R}}^{[\mathrm{L}]}]$$
模块三：交叉注意力上下文异常评分
将提供的$nk$个正常节点作为上下文节点，模型的任务是：基于这些上下文节点，尝试重建或预测每一个待评估的查询节点（Query Node，即除去Context Node剩下的节点）的嵌入。如果一个查询节点很容易被上下文样本重建，那么它是正常的。如果一个查询节点很难被重建，那么它是异常的。
输入查询嵌入（所有待评估节点的残差嵌入$Z_q$）和上下文嵌入（$nk$个已知正常节点的残差嵌入$Z_k$），使用一个交叉注意力块，$Z_q$作为$Query(Q)$，$Z_k$作为$Key(K)$和$Value(V)$，基于上下文$Z_k$对查询$Z_q$计算重建嵌入${\hat{Z}}_q$。
计算原始查询嵌入$Z_q$与重建嵌入${\hat{Z}}_q$之间的距离，这个距离$||Z_q-{\hat{Z}}_q||$就是节点的异常分数。距离越大，说明原始嵌入与正常重建偏差越大，节点越异常。

UNPrompt*_2025

核心目标：构建一个通用的、零样本的图异常检测模型，确保模型的通用性（模型在一个或多个源域图上训练，能直接迁移到完全未见过的、不同领域的目标图上、零样本（在目标图上进行推理时，不需要任何标注数据，即没有提供任何异常或正常节点标签）、有效性（利用学到的通用知识或先验，在新图上也能有效识别异常）。
设计思路：UNPrompt提出了一个两模块的框架：节点属性统一和邻域提示学习。

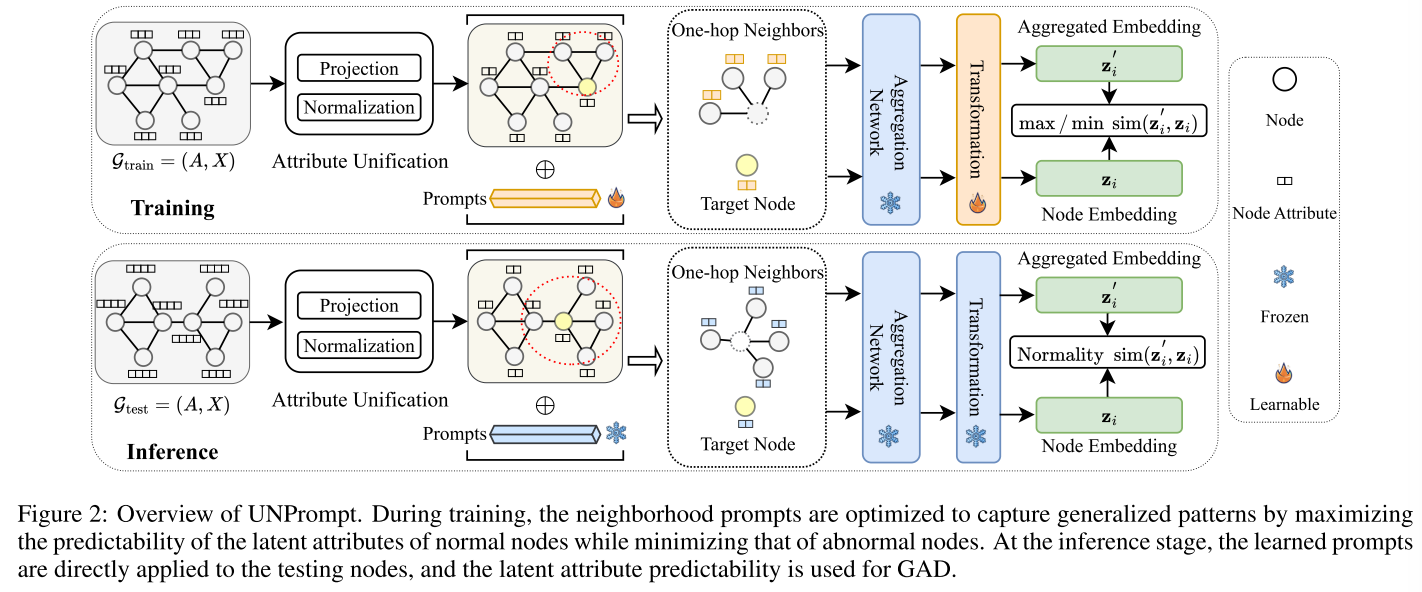
整体流程：
阶段一：节点属性统一
不同图的节点属性维度和语义完全不同，直接比较不同领域图的表示是不可能的。
（1）特征投影
使用一个可学习的线性变换，将所有图的节点属性投影到一个预定义的公共维度，旨在解决维度不匹配问题。
（2）坐标归一化
对投影后的特征进行归一化处理，解决不同图的特征的尺度差异、分布差异，并削弱语义差异，使不同图的维度特征在统计特性上对齐。
阶段二：邻域提示学习
冻结预训练模型，在相同或不同的图上，通过优化“正常节点可预测性高，异常节点可预测性低”的目标，学习一组通用的提示向量和转换网络。
（1）潜在节点属性的可预测性作为异常分数
由于普遍存在的图同态关系，正常节点往往与属性相似的正常节点有更多的联系，导致正常节点中的邻域更加均匀。相反，异常连接或属性的存在使异常节点显著偏离其邻居。因此，对于目标节点，与异常节点相比，如果该节点是正常节点，则其潜在属性基于其邻居的潜在属性更可预测。
通过一个简单的GNN$g$邻居聚合网络得到目标节点的聚合邻域嵌入${\tilde{z}}_i$。同时，直接从归一化的节点属性$\tilde{X}$经过一个简单的线性投影$W$得到节点潜在属性$z_i$。随后，利用余弦相似度衡量每个节点基于领域的潜在属性可预测性$s_i$。
（2）图对比预训练
采用图对比学习，使用InfoNCE损失。
（3）基于潜在属性可预测性的邻域提示
设计了附加在目标节点的邻域节点属性上的可学习提示，核心思想是最大化正常节点的可预测性和最小化异常节点的可预测性，旨在通过快速调整进一步学习更多的广义正常和异常模式，学习稳健的区分模式，在推理过程中不需要重新训练就可以检测出不同不可见图中的异常节点。
对于图中的每个节点，统一特征空间中的节点属性通过提示向量的加权组合来增强，其中每个提示向量的权重从$K$个可学习的线性投影获得：
$${\hat{x}}_i={\bar{x}}_i+\sum _j^K{\alpha }_j{p}_j$$
$\tilde{G}=(A,\bar{X}+P)$被喂给冻结的预训练模型$g$得到相应的聚合嵌入$\tilde{Z}$和节点潜在属性$Z$。为了进一步增强表示区分度，在学习的$\tilde{Z}$和$Z$上应用变换层$h$将它们变换成更具异常区分度的特征空间。
阶段三：推理阶段
输入一个全新的、未见过的目标图$G_{test}$，对$G_{test}$的节点属性应用相同的属性统一模块（投影+归一化），将冻结的GNN模型$g$和冻结的提示向量$P$应用在$G_{test}$上，计算每个节点$v_i$的表示$z_i$和基于其邻域与提示的预测表示${\tilde{z}}_i$，通过余弦相似度计算节点的正常分数。

SpaceGNN*_2025

核心挑战：解决监督式节点异常检测中的一个关键痛点：当可用的标注数据（尤其是异常节点标签）极少时，如何有效训练一个强大的检测模型？
核心思想：
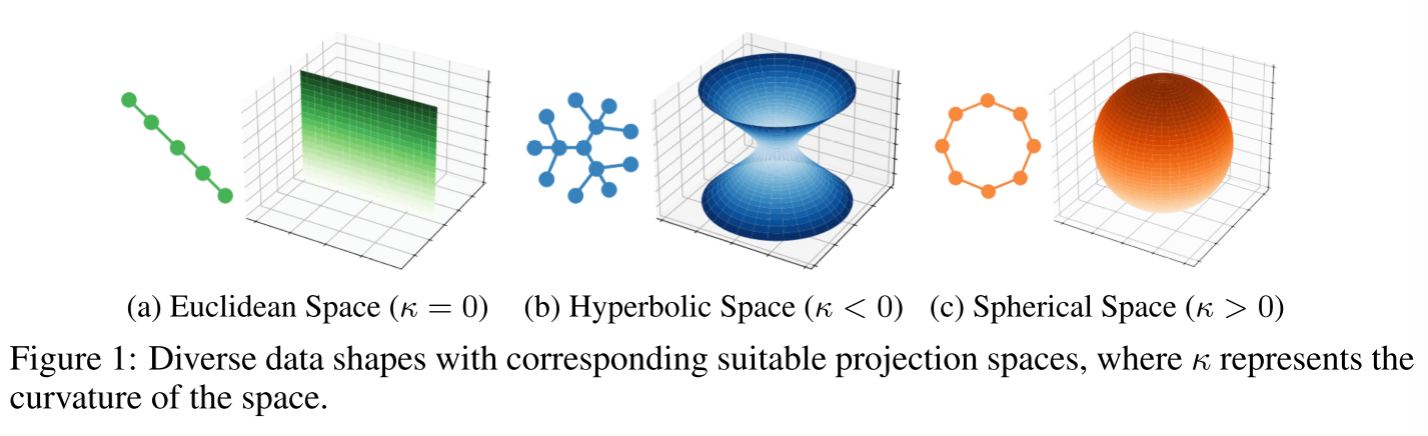
（1）超越欧几里得空间：传统的GNN在欧几里得空间中嵌入节点，但非欧几里得（如双曲面空间、球面空间）可能更适合捕捉图的复杂层次或循环结构。
（2）利用多空间信息：不同的空间（欧式、双曲、球面）对节点表示有不同的偏好。通过在一个框架内融合多个空间的信息，可以获得更全面、更鲁棒的表示。
（3）设计空间感知模块：提出“可学习空间投影”和“距离感知传播”模块，让模型能自适应地利用不同空间的几何特性。
（4）多空间集成优于数据增强：当标签极少时，与其费力地生成可能有噪声的合成数据（数据增强），不如直接集成来自多个独立空间的视图（多空间集成）。

整体框架：
SpaceGNN的核心是$f=\alpha f_0^L+{\sum }_{i=1}^H{\beta }_i{f}_{k_i^{-}}^L+{\sum }_{j=1}^S{\gamma }_j{f}_{k_j^{+}}^L$，$f_0^L$、$f_{k_i^{-}}^L$、$f_{k_j^{+}}^L$分别表示欧式GNN、双曲GNN和球面GNN，即一个多空间集成框架。它由三个关键模块构成，形成一个完整的流程：
模块一：可学习空间投影LSP
传统的GNN通常只在单一的欧几里得空间中操作，不同的图数据或不同的任务可能需要不同的几何空间来最优地表示节点关系（例如，双曲空间适合层次树，球面空间适合循环结构），硬编码选择一个空间可能不是最优的。
SpaceGNN提出“可学习空间投影”，让模型能够自适应地选择或组合不同的几何空间。通过引入一个可学习的曲率参数$k$来控制空间的几何性质：

• $k=0$：对应欧几里得空间；
• $k<0$：对应双曲空间，具有负曲率，适合表示层次和树状结构；
• $k>0$：对应球面空间，具有正曲率，适合表示循环和紧凑结构。

具体操作为：为GNN的每一层$l$引入一个可学习的曲率参数$k_l$，利用$k_l$将节点表示从原始空间投影到一个具有特定曲率$k_l$的空间中。在训练过程中，$k_l$会通过梯度下降进行优化。模型会自动学习到，对于特定的图和任务，哪些层使用哪种曲率最有利于提取异常特征。
模块二：距离感知传播DAP
标准的GNN消息传递通常对所有邻居一视同仁，或使用简单的注意力机制。在非欧几里得空间中，节点间的距离具有更丰富的几何意义，应该被更有效地利用。信息传播应该增强来自同类（正常）节点的有价值信息，同时抑制来自异类（异常）节点的噪声信息。
SpaceGNN提出距离感知传播，并引入了加权同质性$W{H}_k$作为核心概念。$W{H}_k$是一个系数，用于衡量在曲率$k$的空间中，节点$i$和节点$j$之间的同质性或亲和性。在信息传播时，$W{H}_k$作为消息$m_j$传递给$i$的权重，如果$i$和$j$是同类（如都是正常节点），$W{H}_k$应该高，信息被增强。如果$i$和$j$是异类（如一个正常一个异常），$W{H}_k$应该低，信息被抑制。定理一证明了，增大$W{H}_k$（即增强同类边的权重）可以增加节点保持其原始（正常）分布的概率。
在投影后的空间（曲率$k$）中，计算节点$i$和$j$之间的距离$d_k(i,j)$，直接计算$d_k(\cdot ,\cdot )$可能不稳定，定理二提供了一个简单而强大的近似，将非欧式距离与欧式距离和点积联系起来。将计算出的近似距离和节点特征$x_i,x_j$一起输入一个多层感知机（MLP）：$w_{ij}^k=MLP(CONCAT({\mathrm{X}}_i,{\hat{s}}_{ij}{\mathrm{X}}_j))$，其中${\hat{s}}_{ij}$是基于$d_k(i,j)$计算出的相似度（距离越小，相似度越高）。
模块三：多空间集成MSEE
在标签极度有限的监督学习场景下，模型很容易过拟合到少量的训练样本。传统的解决方案是数据增强，例如生成合成数据或伪标签，但论文指出，这种方法可能引入噪声，反而会损害性能。
SpaceGNN提出多空间集成，在不同的几何空间（欧式$f_0^L$、双曲$f_{k_i^{-}}^L$、球面$f_{k_j^{+}}^L$）中训练独立的GNN模型，每个空间提供了看待图数据的不同视角，将这些来自不同空间的模型的预测结果进行集成，形成最终的预测。

AnomalyGFM*_2025

核心挑战：通用的图基础模型通过预训练学习图的普遍规律，这些规律偏向于正常模式，难以捕捉稀少、不规则的异常模式。直接学习异常是困难的，AnomalyGFM转而学习一个通用的正常性度量标准。要让一个模型具备跨域少样本异常检测的能力，必须学习到图无关的正常与异常概念。
核心目标：通过节点表示残差将异常检测问题转化为一个图无关的度量学习问题。

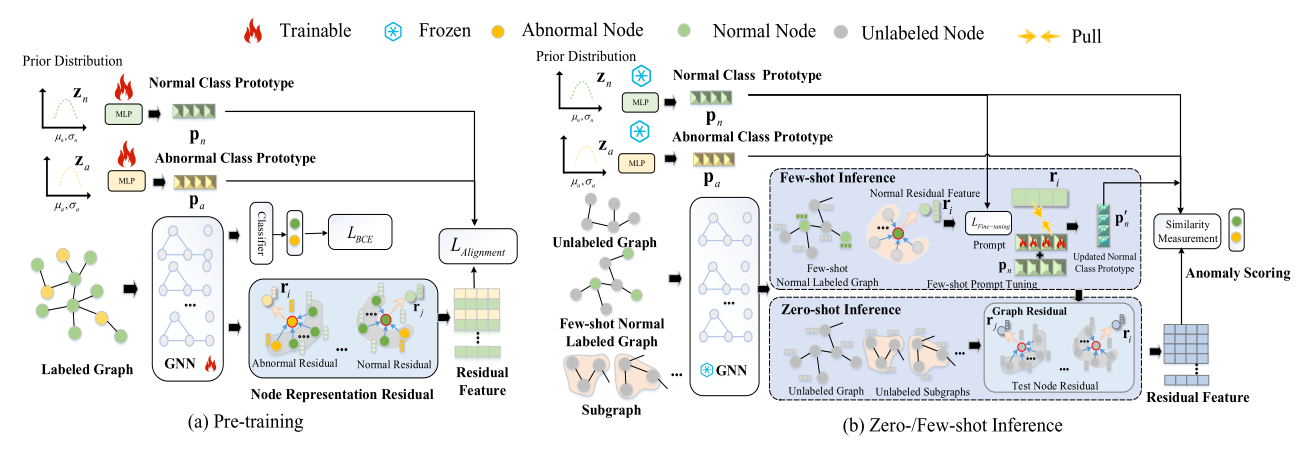
整体流程：
阶段一：预训练过程
（1）节点表示残差
残差特征捕捉了节点的表示与其邻居聚合表示之间的偏差，残差本质上将节点信息投影到一个统一的、以偏离度为度量的特征空间，在该空间中，不同图、不同领域的正常和异常模式可以被一致地衡量和比较，从而实现图无关。
（2）图无关原型对齐
引入两个数据无关的、可学习的向量——正常类原型和异常类原型，这些原型在预训练过程中不断被优化，以代表正常和异常的概念。预训练的目标函数旨在让正常节点的残差聚集在正常类原型附近，让异常节点的残差聚集在异常类原型附近，同时最大化正常类原型和异常类原型之间的距离，确保它们代表截然不同的概念。
阶段二：提示调优过程
（1）正常原型提示
冻结GNN编码器参数和预训练的异常模型，引入可学习的提示和适配层，构建一个新的正常原型。
（2）单类提示微调
最小化标注正常节点的残差与新原型之间的欧式距离，新原型被拉向目标图中真实正常节点的残差中心，从而更好地对齐了目标图的正常模式。

AffinityTune*_2025

核心挑战：给定一个图，其中只有极少数节点有异常标签，目标是判断图中任意节点是否为异常，这是一个少样本图异常检测任务。
核心目标：AffinityTune提出了一种基于亲和力判断的统一框架，并结合提示调优来实现高效的迁移学习。

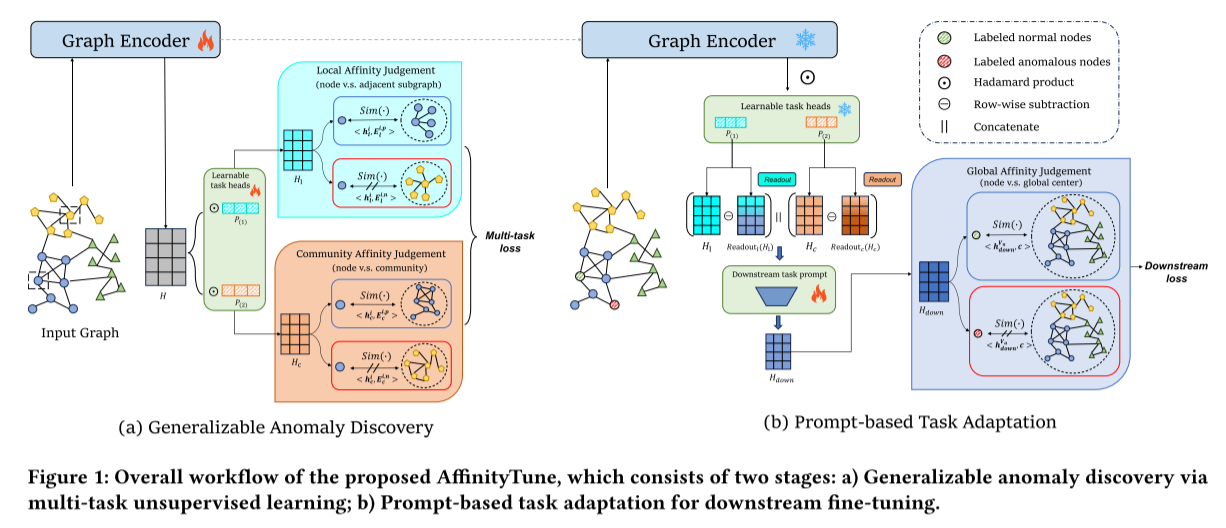
整体流程：
阶段一：可泛化的异常发现
（1）任务模板：亲和力判断
异常节点通常在多个粒度上表现出较低的亲和力，表现在与邻居节点的连接或属性差异大的局部亲和力低和与所属社区的整体模式偏离的社区亲和力低。这个模板将无监督任务的目标与最终的下游任务对齐，确保学到的知识是可泛化的。
（2）多粒度亲和力判断任务
基于上述模板，设计了两种不同粒度的任务：

• 局部亲和力判断（Local Affinity Judgment）：旨在判断一个节点与其一阶邻居构成的子图之间的亲和力，通过重构该子图的结构或属性来实现，如果一个节点与其邻居的连续模式或属性不一致或亲和力低，重构误差就会很大，这暗示它可能是异常的。
• 社区亲和力判断（Community Affinity Judgment）：旨在判断一个节点与其所属社区之间的亲和力，首先通过某种方式（如聚类）识别出社区。然后，计算节点的表示与社区中心的相似度或距离，距离越远，亲和力越低。

通过同时训练这两种任务，模型能够从局部和全局两个视角捕捉到更丰富、更多元化的异常先验知识。
（3）可学习的任务头
为每个任务（局部亲和力、社区亲和力）设计一个独立的、可学习的任务头，而共享同一个GNN编码器，从而允许每个任务独立地学习和提取其特有的异常先验，避免任务间的干扰，在推理时，可以将不同任务头的输出进行融合，得到更鲁棒的异常分数。
阶段二：基于提示的任务适配
利用阶段一学习到的通用知识，并通过提示调优来高效地适应少样本场景。
（1）下游任务重构：全局亲和力判断
将传统的二分类问题重构为一个“节点vs.全局表示”的亲和力判断任务，全局表示计算为图中所有节点特征的均值向量。正常节点通常聚集在全局中心附近，亲和力高，异常节点作为离群点，远离全局中心，亲和力低。这种重构方式与一类分类在超球面上的思想一致，更符合异常检测的本质。
（2）Flex-Prompt：新颖的提示调优策略
传统图提示GraphPrompt对所有节点的每个特征维度进行统一的缩放，GPF/GPF-plus对所有节点进行了统一的平移。Flex-Prompt引入了一个可学习的变换矩阵$W_{down}$，利用局部特征和社区特征对节点特征进行重加权和投影。其中，$W_{down}$允许对不同节点的不同特征进行独立的、非线性的变换（重加权和投影），这比简单的缩放或平移灵活得多。