聚类准确率计算——标签映射(Kuhn-Munkres匈牙利算法)问题的解决(详细并附完整代码)
总结
聚类算法的标签数字没有顺序意义,直接比数字不准。
需要找到一个最佳映射,让聚类组与真实类别匹配正确。
Kuhn-Munkres / 匈牙利算法可以根据混淆矩阵快速找到最佳映射,使得正确匹配样本数最大。
映射之后再算
accuracy_score,才能真实反映聚类效果。
概述:这里将详细、通俗地讲 Kuhn-Munkres 算法(也叫匈牙利算法),它在聚类任务中为什么要用,以及它是如何工作的。
解释一:
1. 问题背景
在聚类任务里,用 KMeans 或 HDBSCAN 给雷达信号分组:
假设有 3 个真实类别:A、B、C
聚类算法也分出了 3 个组:0、1、2
问题是:聚类算法给出的标签数字和真实标签可能完全不一样,比如:
| 样本 | 真实标签 | 聚类标签 |
|---|---|---|
| 1 | A | 2 |
| 2 | B | 0 |
| 3 | C | 1 |
| 4 | A | 2 |
| 5 | B | 0 |
如果你直接用 accuracy_score 来算准确率,就会很低,因为数字不一致,但实际上聚类分组是正确的。
这时候就需要 找一个最佳映射,把聚类标签映射到真实标签,使得匹配的样本数最多。
2. Kuhn-Munkres / 匈牙利算法做什么
Kuhn-Munkres 算法就是用来解决这个问题的:
给定一个“成本矩阵”,找到一一对应的匹配,使得总成本最小(或总收益最大)。
在聚类映射里:
成本矩阵 = 混淆矩阵(confusion matrix)
混淆矩阵里每个元素
(i, j)表示真实标签 i 被聚类为 j 的样本数我们希望找到一一映射,让匹配正确的样本最多
所以在代码里写了:
cm = confusion_matrix(y_true, y_pred) row_ind, col_ind = linear_sum_assignment(-cm)
解释一下:
cm是混淆矩阵:行 = 真实标签
列 = 聚类标签
值 = 样本数
例如:
| 0 | 1 | 2 | |
|---|---|---|---|
| A | 0 | 0 | 2 |
| B | 2 | 0 | 0 |
| C | 0 | 2 | 0 |
行是真实类别 A/B/C
列是聚类标签 0/1/2
linear_sum_assignment(-cm):
因为
linear_sum_assignment是找“最小成本”,而我们希望最大化匹配的数量,所以用-cm。返回两个数组:
row_ind= 每个真实标签对应的行索引col_ind= 对应的聚类标签索引
用这个一一对应关系,就能把聚类标签映射到真实标签。
3. 举例说明
用上面混淆矩阵:
| 0 | 1 | 2 | |
|---|---|---|---|
| A | 0 | 0 | 2 |
| B | 2 | 0 | 0 |
| C | 0 | 2 | 0 |
linear_sum_assignment(-cm)会找出最佳匹配:聚类 0 → 真实标签 B
聚类 1 → 真实标签 C
聚类 2 → 真实标签 A
然后映射聚类标签:
mapping = {0: 'B', 1: 'C', 2: 'A'} y_pred_mapped = [mapping[label] for label in y_pred]
这样一来,聚类标签就和真实标签对齐了,计算准确率才有意义。
4. 总结
聚类算法的标签数字没有顺序意义,直接比数字不准。
需要找到一个最佳映射,让聚类组与真实类别匹配正确。
Kuhn-Munkres / 匈牙利算法可以根据混淆矩阵快速找到最佳映射,使得正确匹配样本数最大。
映射之后再算
accuracy_score,才能真实反映聚类效果。
解释二:
一:聚类准确率如何计算?案例如下
假设{ 1 , 1 , 1 , 2 , 2 , 3 , 4 , 4 , ⋯ , 7 , 7 , 7 , 9 , 9 } \{1,1,1,2,2,3,4,4,\cdots,7,7,7,9,9\}{1,1,1,2,2,3,4,4,⋯,7,7,7,9,9}为真实的数据标签,而利用上述算法对数据聚类之后的标签可能是{ 3 , 3 , 3 , 1 , 1 , 4 , 6 , 6 , ⋯ , 9 , 9 , 7 , 7 , 7 } \{3,3,3,1,1,4,6,6,\cdots,9,9,7,7,7\}{3,3,3,1,1,4,6,6,⋯,9,9,7,7,7},就算在最理想的状态下,把所有该在一个簇中的数据都聚类到一个簇中,但是由于标签的规则不一致,所以每个簇给定的标号不一样。这时候就需要利用到Kuhn-Munkres算法来对标签进行重新标号。
解决方法:利用Kuhn-Munkres算法映射标签
重新标号的主要思路就是,将聚类之后的每一种标签(称为预测标签)与每一种真实标签一一对比,计算出所有标签组合(i,j)情况的数据重合数量,这样就会形成一个“代价矩阵”,基于这个“代价矩阵”,就可以利用Kuhn-Munkres算法来找出代价最低的分配方式,也就是预测标签与真实标签之间的映射关系。
例如,现在具有以下数据(所有数据及代码下载方式见下文),
对于数据lung.mat,具有5种标签,分别为{ 1 , 2 , 3 , 4 , 5 } \{1,2,3,4,5\}{1,2,3,4,5},所以预测标签与真实标签组合之后就会形成一个5 × 5 5\times55×5的矩阵,矩阵中的每个值就代表该标签组合情况下数据的重合数量,例如
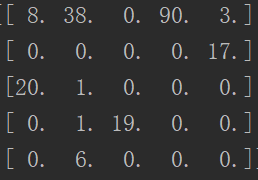
其中第1行第2列数字为38,就代表真实标签为1的数据与预测标签为2的数据重合的数量有38个,以此类推,计算此矩阵代码如下:
for i in range(nClass1):
ind_cla1 = L1 == Label1[i]
ind_cla1 = ind_cla1.astype(float)
for j in range(nClass2):
ind_cla2 = L2 == Label2[j]
ind_cla2 = ind_cla2.astype(float)
G[i, j] = np.sum(ind_cla2*ind_cla1)
这里的代码如果对于Python不熟悉的话可能是比较难以理解的,但是这一部分的思想是真的巧妙,我也不知道怎么去详细解释,如果不懂的话就仔细看看Python中矩阵相关操作吧,尤其是numpy的了解非常重要。
上面我们得到了标签组合矩阵,但是Kuhn-Munkres算法是用来计算最低代价的分配方式的,(不了解Kuhn-Munkres算法的话建议去看这篇博客Kuhn-Munkres算法将聚类后的预测标签映射为真实标签,如果不需要深究具体思路的,只需要了解这个算法能够达到的目的即可),而我们需要的是所有标签对应的数据重复数量最多的映射关系,所以我们可以在这个矩阵前加个负号,就能由求最多变成求最少,如图

然后利用Python集成的Munkres方法计算出标签对应关系为:

意思就是 ,预测标签为1的所有数据的标签需要改成3,以此类推。
原文链接:https://blog.csdn.net/McQueen_LT/article/details/103410503
