Leetcode 深度优先搜索 (14)

499. 迷宫III

由空地和墙组成的迷宫中有一个球。球可以向上（u）下（d）左（l）右（r）四个方向滚动，但在遇到墙壁前不会停止滚动。当球停下时，可以选择下一个方向（必须与上一个选择的方向不同）。迷宫中还有一个洞，当球运动经过洞时，就会掉进洞里。

给定球的起始位置，目的地和迷宫，找出让球以最短距离掉进洞里的路径。 距离的定义是球从起始位置（不包括）到目的地（包括）经过的空地个数。通过’u’, ‘d’, ‘l’ 和 'r’输出球的移动方向。 由于可能有多条最短路径， 请输出字典序最小的路径。如果球无法进入洞，输出"impossible"。

迷宫由一个0和1的二维数组表示。 1表示墙壁，0表示空地。你可以假定迷宫的边缘都是墙壁。起始位置和目的地的坐标通过行号和列号给出。

示例1:

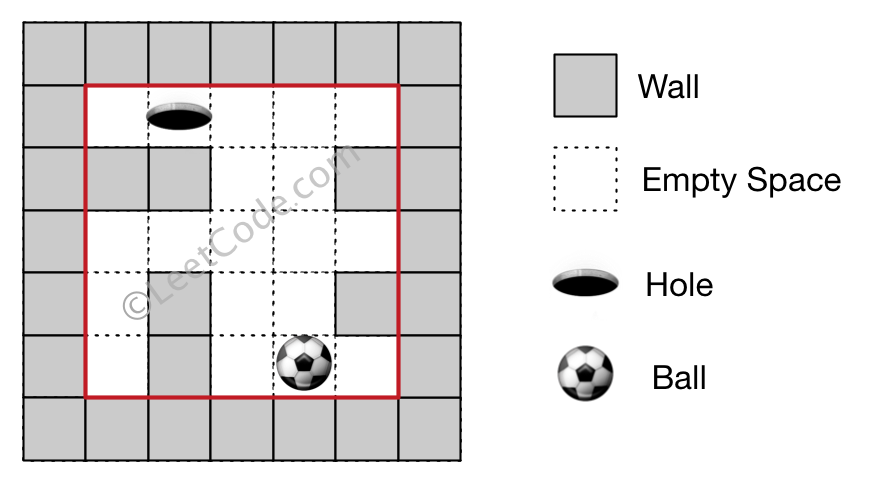
输入 1: 迷宫由以下二维数组表示

0 0 0 0 0
1 1 0 0 1
0 0 0 0 0
0 1 0 0 1
0 1 0 0 0

输入 2: 球的初始位置 (rowBall, colBall) = (4, 3)
输入 3: 洞的位置 (rowHole, colHole) = (0, 1)

输出: “lul”

解析: 有两条让球进洞的最短路径。
第一条路径是 左 -> 上 -> 左, 记为 “lul”.
第二条路径是 上 -> 左, 记为 ‘ul’.
两条路径都具有最短距离6, 但’l’ < ‘u’，故第一条路径字典序更小。因此输出"lul"。

1. BFS（广度优先搜索）+ 字典序优化

核心概念

1. 状态：停靠点 (x, y)（只有撞墙后或落洞才是可选下一方向的停靠点）。
2. 距离：从起点（不计）到当前位置（计）经过的空地数。
3. 目标：最短距离；若距离相同取路径字典序最小（按字符顺序 ‘d’ < ‘l’ < ‘r’ < ‘u’）。
4. 方向选择：一次滚动过程中不能中途停下，因此“不能与上一次方向相同”在这里自然满足（停下后如果还能继续同方向说明之前没撞墙，不会发生）。
5. 洞（hole）特殊：滚动途中经过洞即立刻停止（优先于撞墙）。
6. BFS 适配：虽然每次移动步数不恒定（不是标准无权图），但可以用队列 + 松弛（类似 SPFA）：若发现更短距离或同距更小路径则更新并入队。

维护结构

• dist[m][n]：到该停靠点的当前最短距离（初始化为无穷大）。
• path[m][n]：达到该点的对应最优（最短 + 字典序最小）路径字符串。
• 队列：保存需要继续向外扩展的停靠点。
• 方向数组：按字典序顺序遍历 [‘d’,‘l’,‘r’,‘u’]，并给出对应 (dx, dy)。

扩展步骤

1. 从当前停靠点出发，沿某方向一直滚：计步 step。
2. 滚动过程中若遇洞坐标，立即停下（位置为洞位置；不再继续该方向）。
3. 得到新停靠点 (nx, ny) 与新距离 nd = dist[x][y] + step，新路径 np = path[x][y] + dirChar。
4. 比较：

• 若 nd < dist[nx][ny] → 更新 dist/path，入队。
• 若 nd == dist[nx][ny] 且 np 字典序更小 → 更新 path，入队。

5. 如果 (nx, ny) 就是洞，可继续让算法自然结束；也可在发现当前解优于已知最优时记录，最终输出洞的 path。

终止与结果

• 遍历结束后看 dist[holeX][holeY] 是否仍为无穷：是则 impossible；否则输出 path[holeX][holeY]。
• 起点即洞：直接返回空串 “”（距离 0，路径为空）。

复杂度

• 最多对每个格子进行多次松弛，但每次只有在更优（更短或同距更小字典序）才入队。
• 最坏时间：O(m n * K)，K 与方向尝试及滚动长度有关，近似 O(m n * max(m,n))。
• 空间：$O(mn)$。

class Solution {public String findShortestWay(int[][] maze, int[] start, int[] hole) {int m = maze.length, n = maze[0].length;int sx = start[0], sy = start[1];int hx = hole[0], hy = hole[1];if (sx == hx && sy == hy) return ""; // 起点就是洞// 距离与路径记录int[][] dist = new int[m][n];String[][] path = new String[m][n];for (int i = 0; i < m; i++) {Arrays.fill(dist[i], Integer.MAX_VALUE);Arrays.fill(path[i], null);}dist[sx][sy] = 0;path[sx][sy] = "";// 方向：按要求字典序 d l r uchar[] dirChar = {'d','l','r','u'};int[] dx =     { 1,   0,   0,  -1};int[] dy =     { 0,  -1,   1,   0};Deque<int[]> q = new ArrayDeque<>();q.offer(new int[]{sx, sy});while (!q.isEmpty()) {int[] cur = q.poll();int x = cur[0], y = cur[1];for (int k = 0; k < 4; k++) {char dc = dirChar[k];int nx = x, ny = y;int steps = 0;// 向该方向滚动直到撞墙或进入洞while (true) {int tx = nx + dx[k];int ty = ny + dy[k];if (tx < 0 || tx >= m || ty < 0 || ty >= n || maze[tx][ty] == 1) {break; // 撞墙前一个位置停下}nx = tx;ny = ty;steps++;// 若经过洞，立即停下if (nx == hx && ny == hy) {break;}}// 如果没有移动，跳过if (steps == 0) continue;int newDist = dist[x][y] + steps;String newPath = path[x][y] + dc;// 比较当前停靠点 (nx, ny) 的最优性if (newDist < dist[nx][ny] ||(newDist == dist[nx][ny] && (path[nx][ny] == null || newPath.compareTo(path[nx][ny]) < 0))) {dist[nx][ny] = newDist;path[nx][ny] = newPath;// 若是洞位置，可以继续放入队列也无妨（或选择不入队以微优化）if (!(nx == hx && ny == hy)) {q.offer(new int[]{nx, ny});}}}}return dist[hx][hy] == Integer.MAX_VALUE ? "impossible" : path[hx][hy];}
}

2. Dijkstra算法变体

核心建模

• 视每个“可停下的位置”为图节点（即撞墙后的停点，起点，以及途中若经过洞则提前结束）。
• 边：从当前停点沿某方向滚动到下一个停点（或途中掉入洞）。权重为滚动经过的空格数。
• 目标：最短距离；若距离相同取路径字符串（方向序列）字典序最小。

关键细节

1. 采用优先队列（小根堆），按 (距离, 路径字符串) 排序。
2. 状态：(x, y, dist, path)。
3. 出堆时若位置为洞，直接返回其 path（Dijkstra 保证最优且字典序最小）。
4. dist 记录最短距离；另外用 pathBest 记录在达到同一距离时的最优字典序。
5. 每次从一个停点向四方向模拟“滚到墙前或洞”，途中若遇洞立即停止并生成候选。
6. 方向顺序固定使用字典序 (按题意 ‘d’,‘l’,‘r’,‘u’ 或若题目明确指定顺序则用该顺序)。若未特别指定常用 ‘d’,‘l’,‘r’,‘u’ 或 ‘u’,‘d’,‘l’,‘r’，只要与字典序一致即可；真正裁定由优先队列 comparator 完成。
7. 起点即洞：返回空字符串。
8. 无法到达：返回 “impossible”。

复杂度

• 时间：$O(mnlog(mn))$（每节点最多进堆多次但受剪枝约束）。
• 空间：$O(mn)$。

注意

• 路径字典序判定直接用字符串 compareTo。
• 路径长度计算包含终点但不含起点；实现里 dist 直接累加步数（滚动经过的格子数）。
• “不能与上一次方向相同”在标准滚动模型里自然满足（撞墙后不可能继续同方向），可忽略。

class Solution {public String findShortestWay(int[][] maze, int[] start, int[] hole) {int m = maze.length, n = maze[0].length;int sx = start[0], sy = start[1];int hx = hole[0], hy = hole[1];if (sx == hx && sy == hy) return "";// 方向: 上 下 左 右 (字典序比较依赖最终路径字符串本身，不强制这里的顺序，但为生成更多前缀较小路径，可把 'l' 放前。// 为清晰这里使用固定顺序: u, d, l, rint[][] dirs = { {-1,0}, {1,0}, {0,-1}, {0,1} };char[] dirChars = { 'u','d','l','r' };int[][] dist = new int[m][n];String[][] bestPath = new String[m][n];for (int[] row : dist) Arrays.fill(row, Integer.MAX_VALUE);PriorityQueue<State> pq = new PriorityQueue<>((a,b) -> {if (a.dist != b.dist) return Integer.compare(a.dist, b.dist);return a.path.compareTo(b.path);});dist[sx][sy] = 0;bestPath[sx][sy] = "";pq.offer(new State(sx, sy, 0, ""));while (!pq.isEmpty()) {State cur = pq.poll();if (cur.x == hx && cur.y == hy) return cur.path; // 最优洞路径if (cur.dist > dist[cur.x][cur.y]) continue;if (!cur.path.equals(bestPath[cur.x][cur.y])) continue;for (int k = 0; k < 4; k++) {int nx = cur.x;int ny = cur.y;int steps = 0;boolean fell = false;// 模拟滚动while (true) {int tx = nx + dirs[k][0];int ty = ny + dirs[k][1];if (tx < 0 || tx >= m || ty < 0 || ty >= n || maze[tx][ty] == 1) break;nx = tx; ny = ty; steps++;if (nx == hx && ny == hy) { // 途中掉入洞fell = true;break;}}if (steps == 0) continue;int newDist = cur.dist + steps;String newPath = cur.path + dirChars[k];// 无论是否掉洞，都统一按规则入堆（洞状态出堆时返回）if (newDist < dist[nx][ny] ||(newDist == dist[nx][ny] && (bestPath[nx][ny] == null || newPath.compareTo(bestPath[nx][ny]) < 0))) {dist[nx][ny] = newDist;bestPath[nx][ny] = newPath;pq.offer(new State(nx, ny, newDist, newPath));}}}return "impossible";}private static class State {int x, y, dist;String path;State(int x, int y, int dist, String path) {this.x = x; this.y = y; this.dist = dist; this.path = path;}}}

3. DFS + 剪枝

思路说明（DFS + 剪枝）

1. 状态定义：在一个可停位置 (x,y) 且上一次选择的方向 prevDir（起点为无方向）。只能再选与 prevDir 不同的方向开始滚动。
2. 动作执行：选择一个新方向后沿该方向一直滚到撞墙前的最后一个空格，或在途中经过洞则提前结束（掉入洞，路径完成）。
3. 距离累计：滚动经过的空格数（不含起点，含终点/洞）。
4. 字典序要求：在 DFS 中按方向字符的字典序顺序尝试（这里采用 ‘d’ < ‘l’ < ‘r’ < ‘u’，与常见题目 The Maze III 保持一致），这样当发现某条距离更短或相同且字典序更小的路径时及时更新。
5. 剪枝策略：

• 全局 bestDistance：若当前已走距离 >= bestDistance（已有最优）则剪枝。
• 备忘 bestDist[x][y][prevDirIndex]：记录到达该“停点+前方向”状态的最小距离；若当前距离 > 已记录则无需再继续。

6. 方向不能重复：下一次选择方向必须不同于 prevDir。
7. 终止条件：滚动过程中一旦经过洞立即判断是否更新答案，不再继续该路径。
8. 特殊情况：

• 起点就是洞：返回空串 “”（距离 0）。
• 无法到达：返回 “impossible”。

复杂度

• 最坏可能仍接近指数，但剪枝通常显著减少分支。
• 备忘数组大小 O(m * n * 5)（多一个“无前方向”状态）。
• 每次模拟滚动 $O(max(m,n))$。

public class MazeDFS {/*** 求最短路径（距离最小，若并列则路径字典序最小），不存在返回 "impossible"* 方向字典序：'d' < 'l' < 'r' < 'u'*/public String shortestPath(int[][] maze, int[] start, int[] hole) {int m = maze.length, n = maze[0].length;if (start[0] == hole[0] && start[1] == hole[1]) return ""; // 起点即洞// 方向：按字典序排列：d, l, r, uint[][] dirs = {{ 1, 0},   // d{ 0,-1},   // l{ 0, 1},   // r{-1, 0}    // u};char[] dirChars = {'d','l','r','u'};// bestDist[x][y][k]：到达(x,y)且上一次方向索引为k(0..3)，或4表示“无前方向”状态的最小距离int INF = Integer.MAX_VALUE / 4;int[][][] bestDist = new int[m][n][5];for (int[][] plane : bestDist) {for (int[] arr : plane) Arrays.fill(arr, INF);}bestAnswerPath = "impossible";bestAnswerDist = INF;// 起点“无前方向”索引用 4dfs(maze, start[0], start[1], hole, 4, 0, new StringBuilder(), dirs, dirChars, bestDist);return bestAnswerPath;}// 全局记录private String bestAnswerPath;private int bestAnswerDist;private void dfs(int[][] maze,int x, int y,int[] hole,int prevDirIdx,         // 0..3 对应方向；4 = 无int distSoFar,StringBuilder path,int[][] dirs,char[] dirChars,int[][][] bestDist) {int m = maze.length, n = maze[0].length;// 备忘剪枝：若当前距离不优if (distSoFar >= bestDist[x][y][prevDirIdx]) return;bestDist[x][y][prevDirIdx] = distSoFar;// 已有更优全局解（距离更小），且本状态继续走只会更远if (distSoFar >= bestAnswerDist) return;for (int d = 0; d < dirs.length; d++) {if (d == prevDirIdx) continue; // 不可同方向连续int nx = x, ny = y;int steps = 0;boolean fell = false;// 模拟滚动while (true) {int tx = nx + dirs[d][0];int ty = ny + dirs[d][1];// 撞墙则停止于当前 nx,nyif (tx < 0 || tx >= m || ty < 0 || ty >= n || maze[tx][ty] == 1) break;nx = tx; ny = ty;steps++;// 途中经过洞立即结束if (nx == hole[0] && ny == hole[1]) {fell = true;break;}}if (steps == 0) continue; // 该方向无法移动int newDist = distSoFar + steps;// 剪枝：如果新距离已不优于当前最佳if (newDist > bestAnswerDist) continue;path.append(dirChars[d]);if (fell) {// 更新答案：更短 或 相同但字典序更小if (newDist < bestAnswerDist ||(newDist == bestAnswerDist && lexSmaller(path.toString(), bestAnswerPath))) {bestAnswerDist = newDist;bestAnswerPath = path.toString();}// 回溯path.deleteCharAt(path.length() - 1);continue;}dfs(maze, nx, ny, hole, d, newDist, path, dirs, dirChars, bestDist);// 回溯path.deleteCharAt(path.length() - 1);}}private boolean lexSmaller(String a, String b) {if ("impossible".equals(b)) return true;return a.compareTo(b) < 0;}
}