[e3nn] 等变神经网络 | 线性层o3.Linear | 非线性nn.Gate
第4章:等变神经网络模块
欢迎回来~
在我们探索e3nn的旅程中,我们已经揭示了一些基本概念:
- 在第1章:不可约表示(Irreps)中,我们学习了
Irreps作为等变数据的标签,告诉我们数据在旋转和反射下如何变换。 - 在第2章:球谐函数中,我们看到了这些抽象的
Irreps如何通过方向性的"波模式"具体表示。 - 在第3章:张量积中,我们发现了
e3nn如何结合不同的Irreps来创建新的、更复杂的等变特征。
现在,我们有了这些惊人的构建块。但我们如何实际构建一个神经网络呢?在传统神经网络中,我们有"层",如Linear变换和激活函数(如ReLU或Sigmoid)。我们如何创建这些层的等变版本?
这就是等变神经网络模块的用武之地。
这些是您用来构建一个固有尊重3D对称性的神经网络的实际构建块。
它们在底层利用Irreps和TensorProduct来确保当输入旋转或反射时,网络的输出正确变换,就像物理定律一样。
本章的目标是理解如何使用e3nn来创建:
- 一个等变线性变换,类似于
torch.nn.Linear层。 - 一个等变非线性(激活函数),类似于
torch.nn.ReLU。
让我们开始吧~
等变线性层:e3nn.o3.Linear
就像标准线性层将其输入乘以权重矩阵一样,e3nn.o3.Linear层对其输入特征执行线性变换。
关键区别在于它以等变的方式执行。
e3nn.o3.Linear的功能
e3nn.o3.Linear层接受由irreps_in描述的输入特征,并将其转换为由irreps_out描述的输出特征。
关键约束是Linear层只能组合相同Irrep类型的组件。
例如,输入中的所有0e组件可以贡献给输出中的所有0e组件,输入中的所有1o组件可以贡献给输出中的所有1o组件。但0e输入不能通过简单的线性层变为1o输出。
这确保了数据的基本对称属性得以保留。
可以把它想象成整理袜子:
可以将白袜子与其他白袜子组合,彩色袜子与其他彩色袜子组合。
但不能通过简单的重新排列将白袜子"变成"彩色袜子。e3nn.o3.Linear保持了这些"类型"。
如何使用e3nn.o3.Linear
通过使用不可约表示(Irreducible Representations)对象指定其irreps_in和irreps_out来定义e3nn.o3.Linear层。
import torch
from e3nn import o3# 定义输入数据的Irreps:
# 一个标量(0e)和一个向量(1o)的混合
irreps_in = o3.Irreps("0e + 1o")
print(f"输入Irreps: {irreps_in}")# 创建符合这些Irreps的随机输入数据
x = irreps_in.randn(10, -1) # 10个样本,其中-1被irreps_in.dim(4)替换
print(f"输入数据形状: {x.shape}")# 定义输出数据的Irreps:
# 两个标量(0e)和两个向量(1o)的混合
irreps_out = o3.Irreps("2x0e + 2x1o")
print(f"输出Irreps: {irreps_out}")# 创建一个将'irreps_in'数据转换为'irreps_out'数据的线性层
# e3nn确保此层尊重旋转/反射
linear_layer = o3.Linear(irreps_in=irreps_in, irreps_out=irreps_out)
print(f"\n线性层创建: {linear_layer}")# 将线性层应用于输入数据
y = linear_layer(x)
print(f"输出数据形状: {y.shape}")
输出:
输入Irreps: 1x0e+1x1o
输入数据形状: torch.Size([10, 4])
输出Irreps: 2x0e+2x1o线性层创建: Linear(1x0e+1x1o -> 2x0e+2x1o | 10 weights)
输出数据形状: torch.Size([10, 8])
如所见,Linear层成功地将输入(维度4)转换为输出(维度8),就像常规的torch.nn.Linear一样。
e3nn的魔力在于这种转换保证是等变的。
底层实现:e3nn.o3.Linear
当创建e3nn.o3.Linear层时,e3nn智能地确定输入Irreps的哪些部分可以连接到输出Irreps的哪些部分。
具体来说,它知道只有相同l和p的Irrep可以连接。
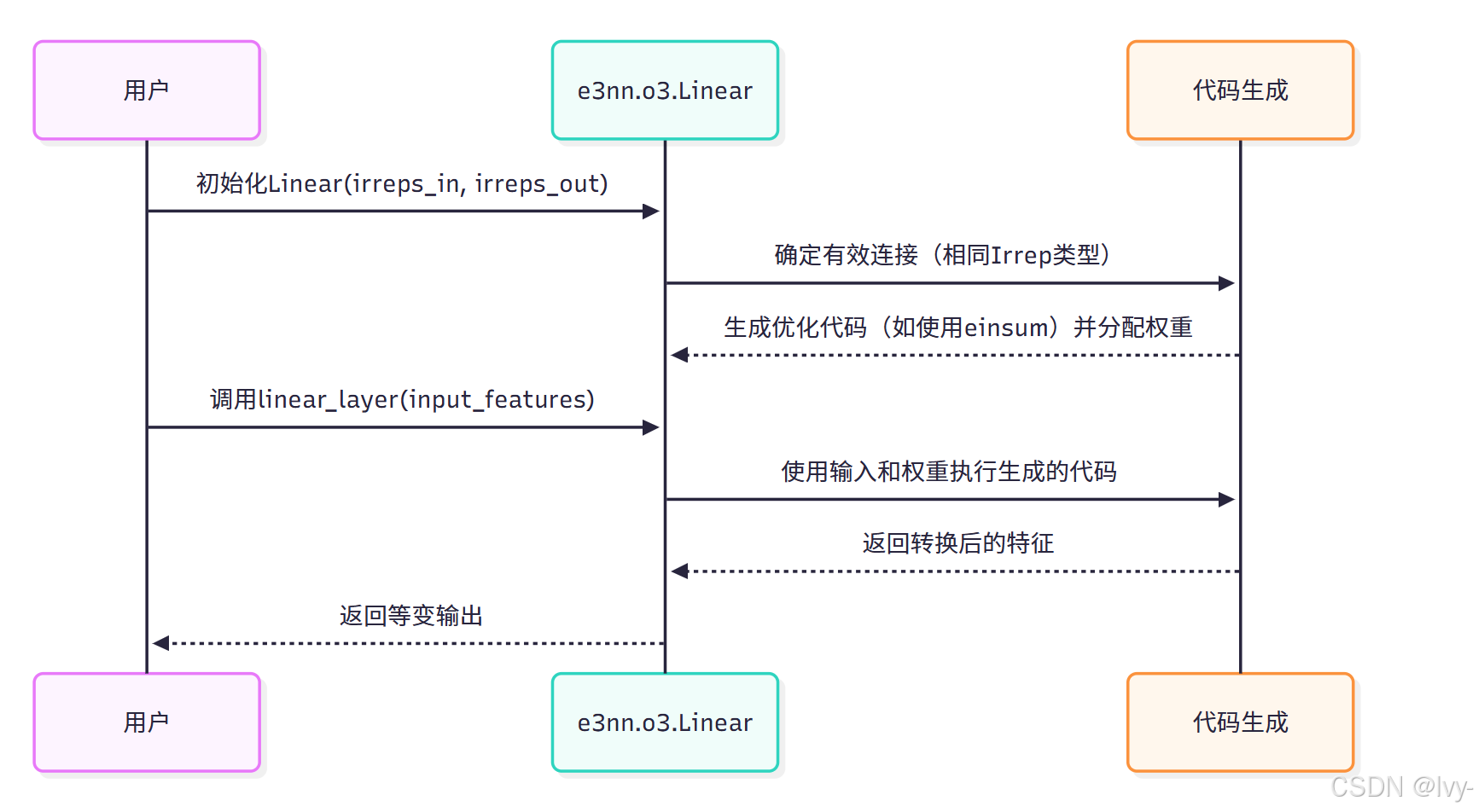
- 连接逻辑:
e3nn识别irreps_in和irreps_out之间所有可能的连接,其中Irrep类型(如0e到0e,1o到1o)匹配。 - 权重分配:对于每个有效连接,它分配一个可学习的权重矩阵。此矩阵的大小取决于输入和输出
Irreps的multiplicity。例如,如果输入中有2x0e,输出中有3x0e,则需要一个2x3权重矩阵用于该连接。 - 高效计算:
e3nn的内部代码(在e3nn/o3/_linear.py中)生成高度优化的torch.einsum操作,而不是手动拆分输入并为每个Irrep类型应用矩阵乘法。einsum是一个强大的函数,允许简洁高效的张量收缩,有效地执行给定输入张量所需的所有乘法和求和,确保等变性和良好的性能。
Linear模块确保每个输入Irrep组件(mul_in x ir_in)仅当ir_in == ir_out时转换为每个输出Irrep组件(mul_out x ir_out)。然后使用大小为mul_in x mul_out的权重矩阵进行此转换。
等变非线性:e3nn.nn.Gate
非线性对于神经网络学习复杂模式至关重要。
然而,直接将标准激活函数(如ReLU或Sigmoid)应用于向量组件会破坏等变性。
如果旋转一个向量(x, y, z),然后对每个组件应用ReLU,这与先应用ReLU再旋转不同。
e3nn.nn.Gate模块提供了一种巧妙的方式引入非线性,同时严格保持等变性。
e3nn.nn.Gate的功能
Gate通过将高阶Irreps(如向量,l=1,或张量,l=2)与标量(0e Irreps的组件)相乘来实现非线性,这些标量首先通过标准激活函数传递。
可以这样理解:
- **标量(
0eIrreps)**可以直接应用正常激活函数(如tanh、sigmoid、relu),因为标量在旋转下不会改变。 - **高阶
Irreps(l > 0)**不能直接应用标准激活。相反,e3nn.nn.Gate使用另一个标量(我们称之为"门")来乘以这些高阶Irreps。这种乘法缩放高阶特征,但不改变其方向或旋转方式。就像灯的调光器开关——它改变亮度(大小),但不改变光的颜色或方向。
这种标量乘法是张量积的特殊情况:0e x Irrep -> Irrep。当您将标量乘以任何其他Irrep时,结果Irrep具有与非标量Irrep相同的l和p。这就是如何保持等变性。
如何使用e3nn.nn.Gate
code: https://github.com/lvy010/AI-exploration/tree/main/neural_network
Gate模块接受五个主要参数:
irreps_scalars:仅作为标量并接收直接激活的特征的Irreps。act_scalars:irreps_scalars的激活函数列表。irreps_gates:用作"门"的特征的Irreps。这些必须是标量(0e)并接收直接激活。act_gates:irreps_gates的激活函数列表。irreps_gated:将被激活门乘以的特征的Irreps。irreps_gates中的Irrep组数必须匹配irreps_gated。
import torch
from e3nn import o3
from e3nn.nn import Gate# 示例:假设输入特征是两个标量和一个向量
# 输入将是:1x0e(标量特征)+ 1x0e(门标量)+ 1x1o(向量特征)
irreps_in = o3.Irreps("1x0e + 1x0e + 1x1o")
x = irreps_in.randn(1, -1)
print(f"输入Irreps: {irreps_in}")
print(f"输入数据形状: {x.shape}")# 定义Gate模块:
# - 第一个0e将直接激活(无门控)。
# - 第二个0e将被激活并用作门。
# - 1o将由激活的第二个0e门控。
equivariant_gate = Gate(irreps_scalars="1x0e", # 一个0e标量act_scalars=[torch.tanh], # 对其应用tanhirreps_gates="1x0e", # 一个0e标量作为门act_gates=[torch.sigmoid], # 对门标量应用sigmoidirreps_gated="1x1o" # 一个1o向量被门控
)
print(f"\n等变Gate创建: {equivariant_gate}")
print(f"输出Irreps: {equivariant_gate.irreps_out}")# 将Gate应用于输入数据
y = equivariant_gate(x)
print(f"输出数据形状: {y.shape}")# 让我们手动拆分输入以检查输出(简化说明)
# scalars_input = x[:, irreps_in.slices_by_irreps[0]]
# gates_input = x[:, irreps_in.slices_by_irreps[1]]
# gated_input = x[:, irreps_in.slices_by_irreps[2]]# print(f"\n(手动说明):")
# print(f"激活标量: {torch.tanh(scalars_input)}")
# print(f"激活门: {torch.sigmoid(gates_input)}")
# print(f"门控向量: {torch.sigmoid(gates_input) * gated_input}")
输出:
输入Irreps: 1x0e+1x0e+1x1o
输入数据形状: torch.Size([1, 5])等变Gate创建: Gate(1x0e+1x0e+1x1o -> 1x0e+1x1o)
输出Irreps: 1x0e+1x1o
输出数据形状: torch.Size([1, 4])
注意输出Irreps 1x0e+1x1o如何组合激活的irreps_scalars和被irreps_gates乘以后的irreps_gated。
irreps_gates本身不出现在输出中,因为它们在乘法中被消耗。总维度从5缩小到4(1x0e(激活标量)+ 1x1o(门控向量))。
底层实现:e3nn.nn.Gate
e3nn.nn.Gate模块(位于e3nn/nn/_gate.py)执行以下步骤:
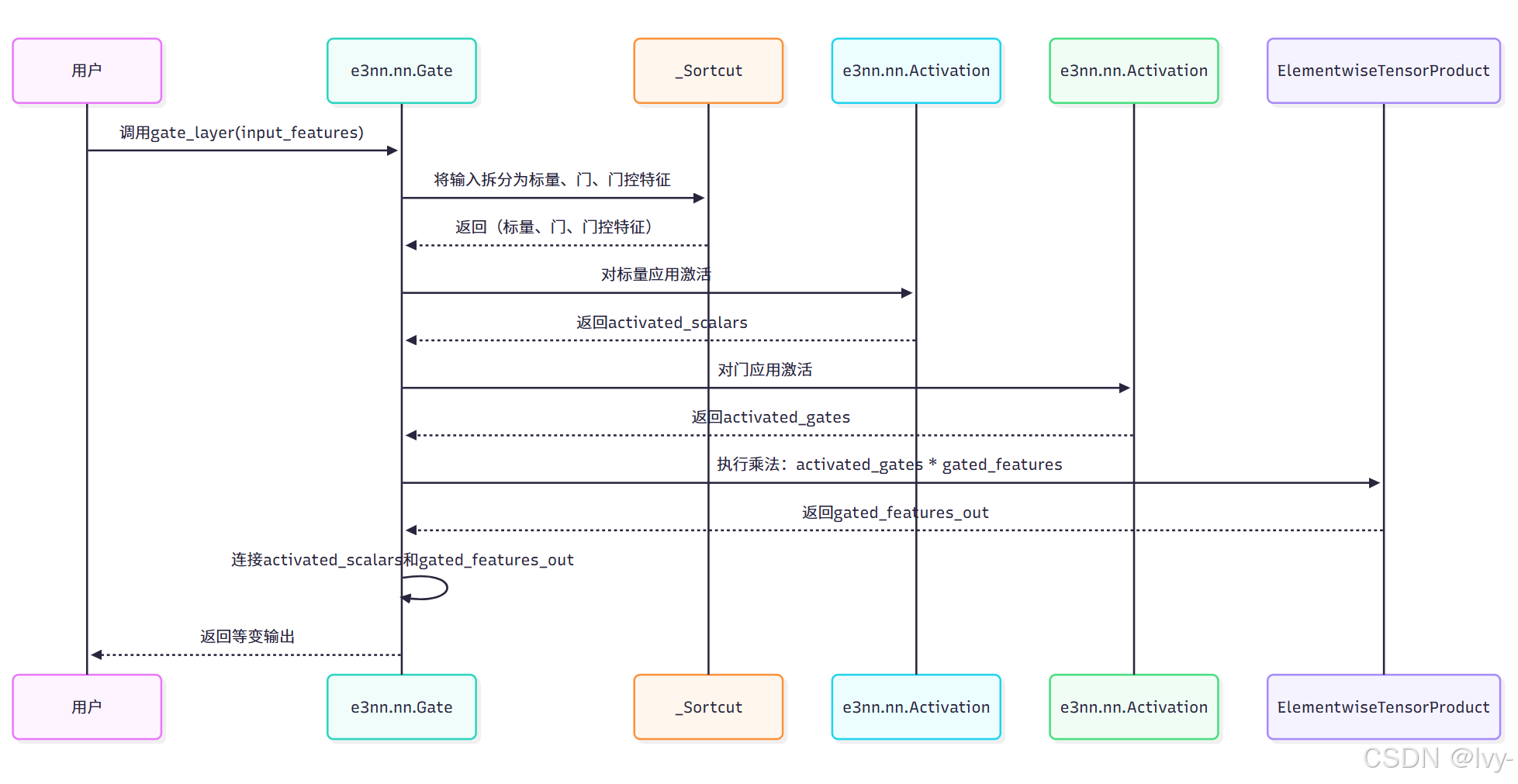
- 特征拆分:首先将输入张量(组合了所有
irreps_scalars、irreps_gates和irreps_gated组件)拆分为其相应部分。这是由内部_Sortcut实用程序处理的,以高效提取张量的正确部分。 - 标量激活:
irreps_scalars和irreps_gates(均为0e类型)通过标准的e3nn.nn.Activation模块传递,应用其各自的非线性函数(如tanh、sigmoid)。 - 门控(张量积):然后,激活的标量门与
irreps_gated特征逐元素相乘。这是由e3nn.o3.ElementwiseTensorProduct(张量积的一种专门形式)执行的,确保标量-Irrep乘法保持等变性。 - 连接:最后,激活的标量和新的"门控"特征被连接在一起,形成输出张量。
这种精心设计的过程允许e3nn在神经网络中引入非线性,而不破坏其等变性的基本承诺。
结论
在本章中,学习了构成e3nn网络层的基本等变神经网络模块:
- **
e3nn.o3.Linear**执行等变线性变换,连接相同类型的Irreps。 - **
e3nn.nn.Gate**以等变方式引入非线性,特别是通过使用激活的标量Irreps来"门控"(乘以)高阶Irreps。
这些模块建立在不可约表示(Irreducible Representations)、球谐函数和张量积的概念之上,构建了固有感知3D对称性的神经网络。有了这些工具,现在可以开始组装强大的等变模型。
然而,就像传统神经网络一样,原始特征值可能会剧烈变化,导致训练不稳定。
在下一章中,我们将探索专门为e3nn设计的==归一化技术,以保持特征值的良好行为==。
第5章:归一化
