当前位置：首页 > news >正文

PAT 1081 Rational Sum

news 2025/8/25 7:45:22

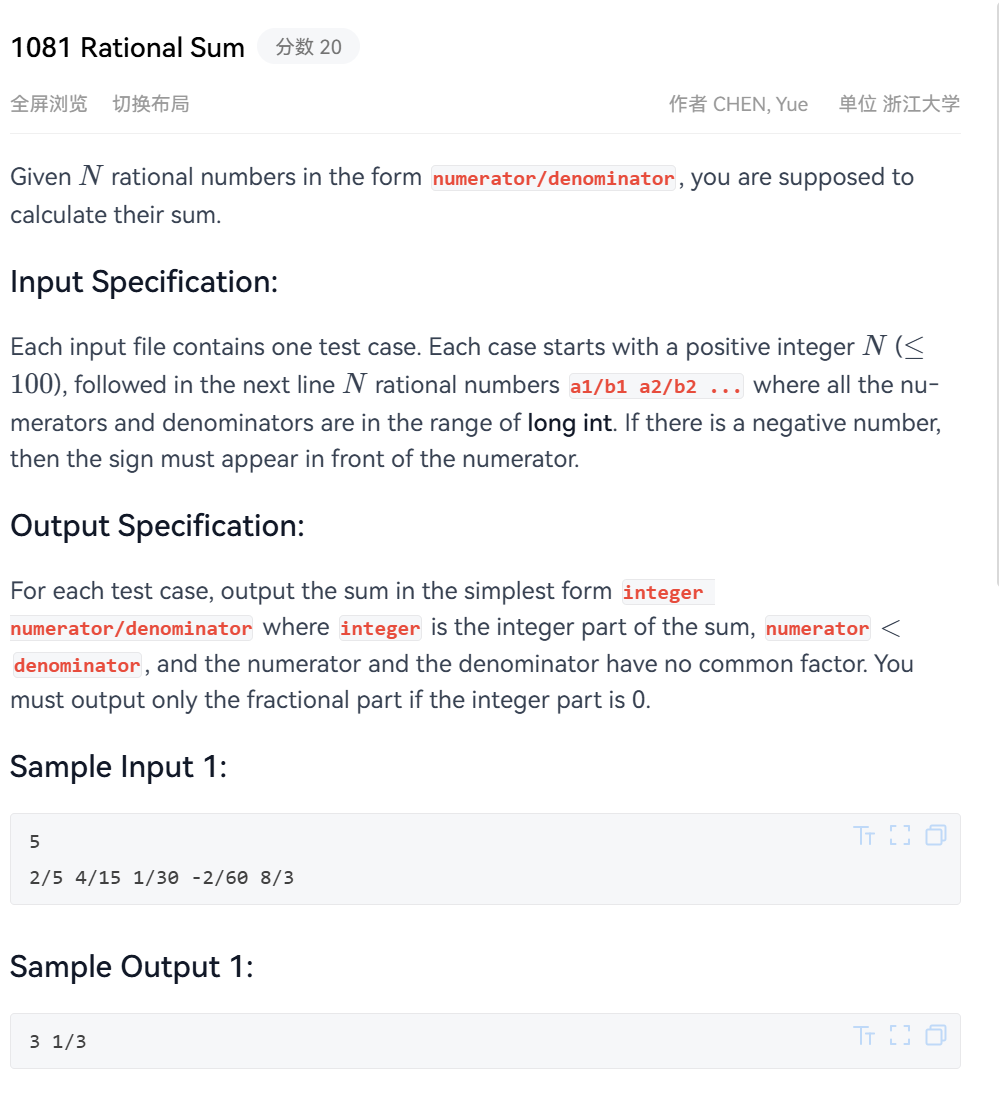
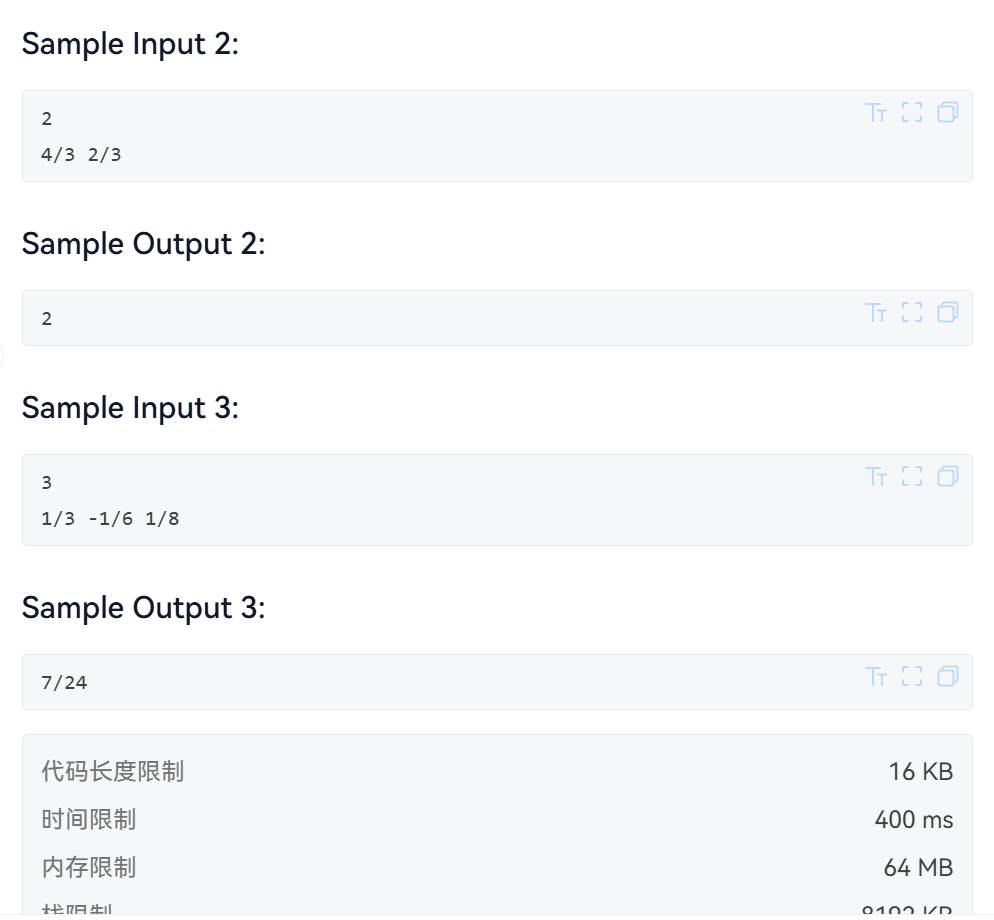
在这里插入图片描述

这一题是模拟分数相加的过程，涉及到通分和约分，大意是给出N个分数，计算它们相加后的结果，要求最终化为最简。
通分和约分涉及到了最小公倍数和最大公因数，其他过程模拟即可。
这里复习一下最大公因数和最小公倍数的求法:

long long gcd(long long x,long long y)
{if(y==0){return x;}else{return gcd(y,x%y);}
}
long long lcm(long long x,long long y)
{return x/gcd(x,y)*y;
}

完整的代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <unordered_map>
#include <limits.h>
#include <queue>
using namespace std;
int N; 
long long a[105];
long long b[105];
long long gcd(long long x,long long y)
{if(y==0){return x;}else{return gcd(y,x%y);}
}
long long lcm(long long x,long long y)
{return x/gcd(x,y)*y;
}
int main()
{//ios::sync_with_stdio(0),cin.tie(0),cout.tie(cin>>N;long long x;for(int i=0;i<N;i++){cin>>a[i];scanf("/");cin>>b[i];if(i==0){continue;}if(i==1){x=lcm(b[i-1],b[i]);}else{x=lcm(x,b[i]);}}if(N==1){if(a[0]==0){cout<<"0";return 0;}long long temp=gcd(a[0],b[0]);long long p=a[0]/abs(temp);long long q=b[0]/abs(temp);//	cout<<p<<" "<<q<<endl;if(p>0){//说明是正数if(p<q){cout<<p<<"/"<<q<<endl;	}	else if(p==q){cout<<"1"<<endl;}else{cout<<p/q<<" ";if(p/q*q<p)cout<<p-p/q*q<<"/"<<q;}} else if(p==0){cout<<"0"<<endl;}else{if(abs(p)>q){cout<<p/q<<" ";if(p/q*q>p)cout<<p-p/q*q<<"/"<<q;	   }else if(abs(p)==q){cout<<"-1"<<endl;	} else{cout<<p<<"/"<<q<<endl;}}return 0;}//算出来的是最小公倍数long long sum=0;for(int i=0;i<N;i++){if(b[i]!=x){a[i]=a[i]*(x/b[i]);}sum+=a[i];} if(sum==0){cout<<"0";return 0;}//	cout<<sum<<" "<<x<<endl;//sum是一个数//x是一个数//如果sum>x//那么 
//	 cout<<sum<<"/"<<x<<endl;long long temp=gcd(sum,x);long long p=sum/abs(temp);long long q=x/abs(temp);//cout<<p<<" "<<q<<endl;if(p>q){if(p%q==0){cout<<p/q;return 0;}cout<<p/q<<" ";if(p/q*q<p)cout<<p-p/q*q<<"/"<<q;	} else if(p==q){cout<<"1";	}else if(p<0){if(abs(p)>q){cout<<p/q<<" ";if(p/q*q>p)cout<<p-p/q*q<<"/"<<q;}else if(abs(p)==q){cout<<p;}else{cout<<p<<"/"<<q;}}else{cout<<p<<"/"<<q;}return 0;}