C++算法学习专题:二分查找
接下来我们将学习经典的算法思想:二分查找
相关习题代码已经上传至作者的个人gitee:CPP 学习代码库: C++代码库新库,旧有C++仓库满员了喜欢请支持一下谢谢。
二分查找是一种在有序数组中快速查找特定元素的高效算法,其时间复杂度为O(log n),远比线性查找的O(n)要快得多。这种算法思想最早可以追溯到1946年由约翰·莫奇利提出的概念。
目录
基本原理
注意事项
二分查找的特点
二分查找的模板
朴素二分查找模板
普通二分查找模板
左边界
右边界
实际应用场景
1、二分查找
2、在排序数组中查找元素的第一个和最后一个位置
3、x的平方根
4、搜索插入位置
5、山脉数组的峰顶索引
6、寻找峰值
7、寻找旋转排序数组的最小值
8、0~n-1中缺失的数字
基本原理
- 前提条件:数组必须是有序的(升序或降序)
- 查找过程:
- 首先确定数组的中间位置 mid = (left + right)/2
- 将要查找的值与中间元素比较
- 如果相等则返回索引
- 如果查找值较小,则在左半区继续查找
- 如果查找值较大,则在右半区继续查找
- 终止条件:找到目标值或搜索区间为空
注意事项
- 边界条件处理要小心,避免无限循环
- 对于重复元素,标准二分查找不能保证返回第一个或最后一个匹配项
- 可以通过变种实现查找第一个/最后一个出现的位置
二分查找的特点
细节多且容易忽略,边界条件多,容易写出死循环。但是当我们掌握后二分查找便会很简单。
二分查找的模板
朴素二分查找模板
while (left <= right){int mid = left + (right - left) / 2;//防止溢出if (。。。。。。){right = mid - 1;}else if (。。。。。。){left = mid + 1;}else if (。。。。。。){return。。。。。。;}省略部分根据二段性填充
普通二分查找模板
左边界
while (left < right)
{int mid = left + (right - left) / 2;if (。。。。。。) left = mid + 1;else right = mid;
}右边界
while (left < right)
{int mid = left + (right - left + 1) / 2;if (。。。。。。) left = mid;else right = mid - 1;
}下面出现-1的时候,上面+1即可
实际应用场景
- 在电话簿中查找联系人
- 在字典中查找单词
- 在游戏排行榜中查找玩家分数
- 在大型数据库中进行快速检索
1、二分查找

算法思路;这道题就是朴素的二分查找算法
定义left为左区间,right为右区间,mid为中间点。
当x< target时,left=mid+1,在[left,right]
当x >target时,right=mid-1,在[left,right]
当x= target时,返回mid
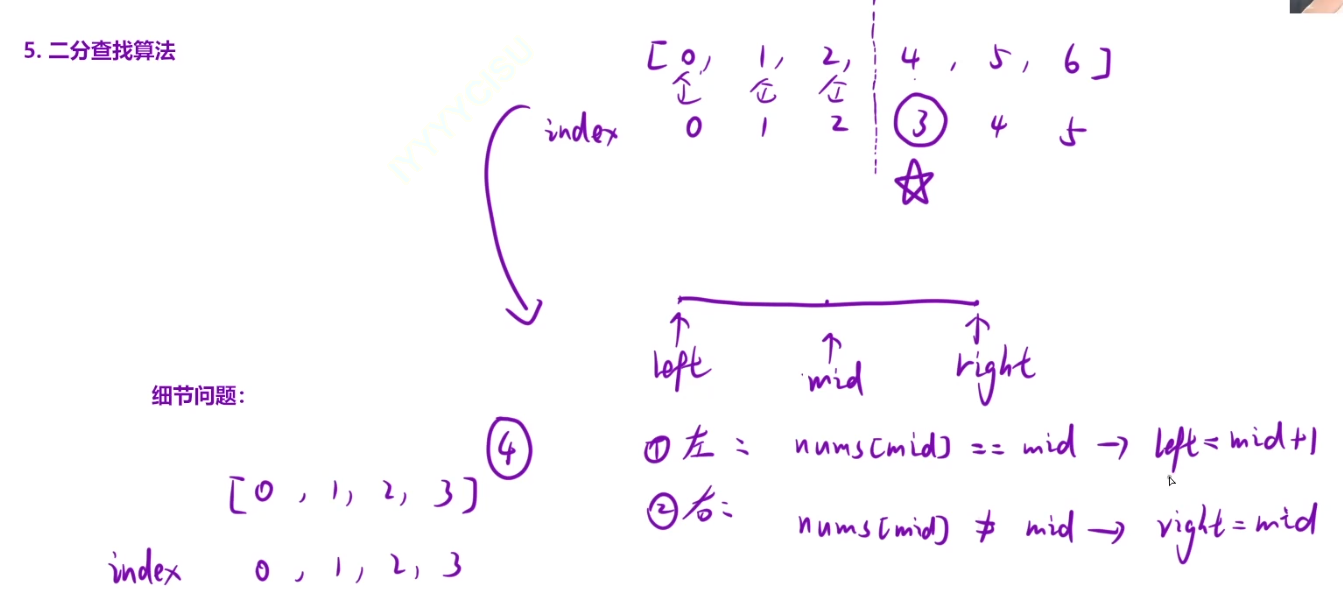
细节问题:
1、循环结束条件
left和right不能缩小为一个点
2、二分查找的正确性
利用数组有序性,进行比较后舍弃了一半数据
3、为什么二分查找时间复杂度很快?
复杂度与循环次数有关,循环与x有关
进行1次循环后数据剩余n/2, 进行1次循环后数据剩余n/4;进行x次后剩余一个。剩余n/2^x,即x=logN
class Solution {
public:int search(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<=right){ int mid=left+(right-left)/2; //防止溢出if(nums[mid]>target){right=mid-1;}else if(nums[mid]<target){left=mid+1;}else if(nums[mid]==target){return mid;}} return -1;}
};2、在排序数组中查找元素的第一个和最后一个位置

算法思路:利用二段性
1、先查找区间左端点
x<t时,left=mid+1,[left,right]
x>=t时,right=mid,[left,right]
细节处理:
(1)循环条件
left<right,原因如下:
left=right的时候就是结果,不需要判断,判断就会陷入死循环
(2)求重点的操作
两种求法:
left+(right-left)/2
left+(right-left+1)/2
区别:数组为偶数的时候第一种为靠左的位置,第二种为靠右的位置
极端情况下(如下)第二种方法就会死循环
2、查找区间右端点
x<=t时,left=mid,[left,right]
x>t时,right=mid-1,[left,right]
循环条件同上;求中点方式用left+(right-left+1)/2,因为用left+(right-left)/2会死循环
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {//数组为空的特殊情况,处理边界情况if(nums.size()==0) return {-1,-1};int begin=0;//查找左端点int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1; else right=mid;} //判断是否有结果if(nums[left]!=target) return {-1,-1};else begin=left;//标记左端点//查找右端点left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]<=target) left=mid; else right=mid-1;}return {begin,right};}
};3、x的平方根

算法思路:
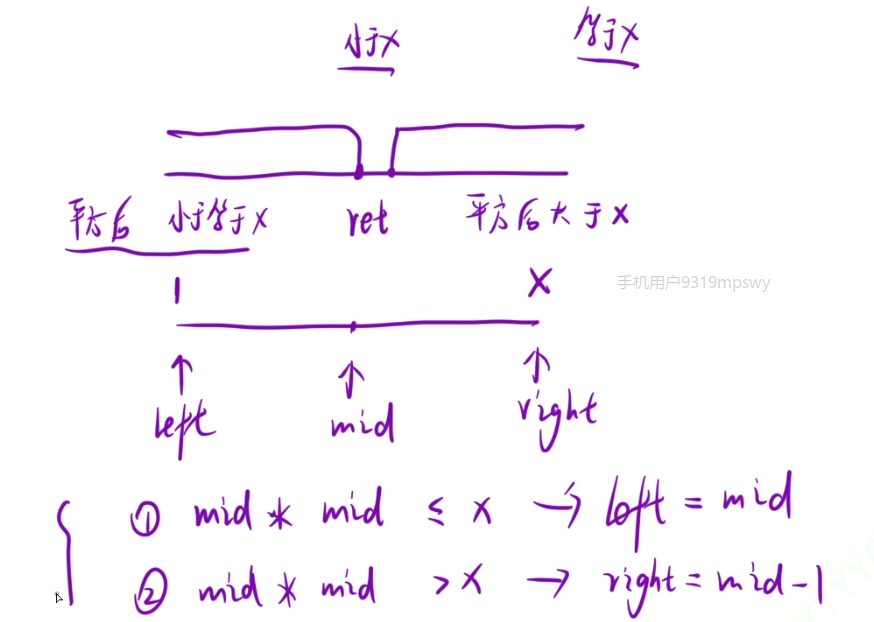
class Solution {
public:int mySqrt(int x) {//处理边界条件if(x<1) return 0;int left=1,right=x;while(left<right){long long mid=left+(right-left+1)/2;//用long long而不用int来防止溢出if(mid*mid<=x) left=mid;else right =mid-1;}return left;}
};4、搜索插入位置

算法思路:
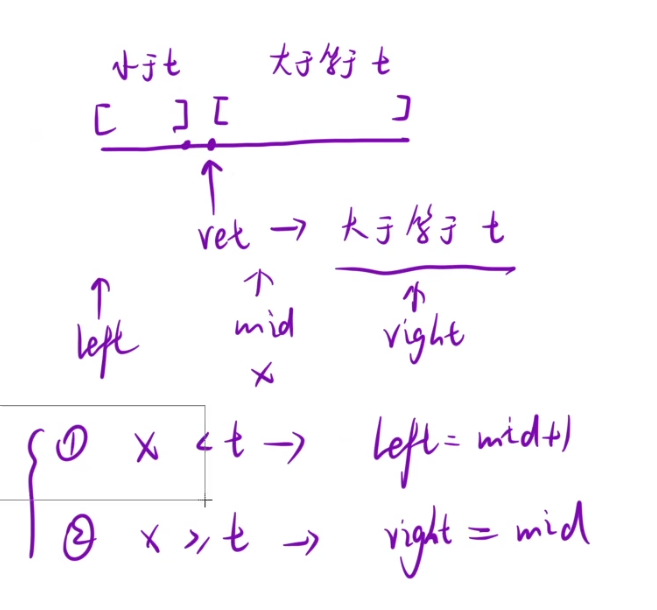
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right=mid;}return nums[left]<target?left+1:left; }
};5、山脉数组的峰顶索引


算法思路: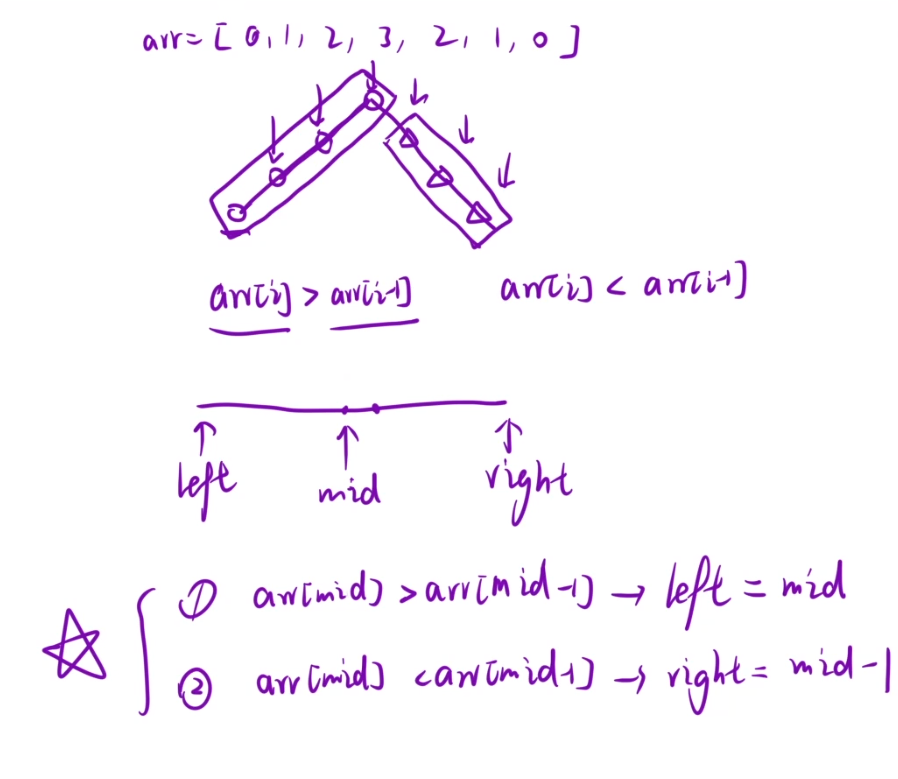
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left=1,right=arr.size()-2;//减少判断次数,因为边缘的点不可能是最值while(left<right){int mid=left+(right-left+1)/2;if(arr[mid]>arr[mid-1]) left=mid;else right=mid-1;}return left;}
};6、寻找峰值

算法思路:
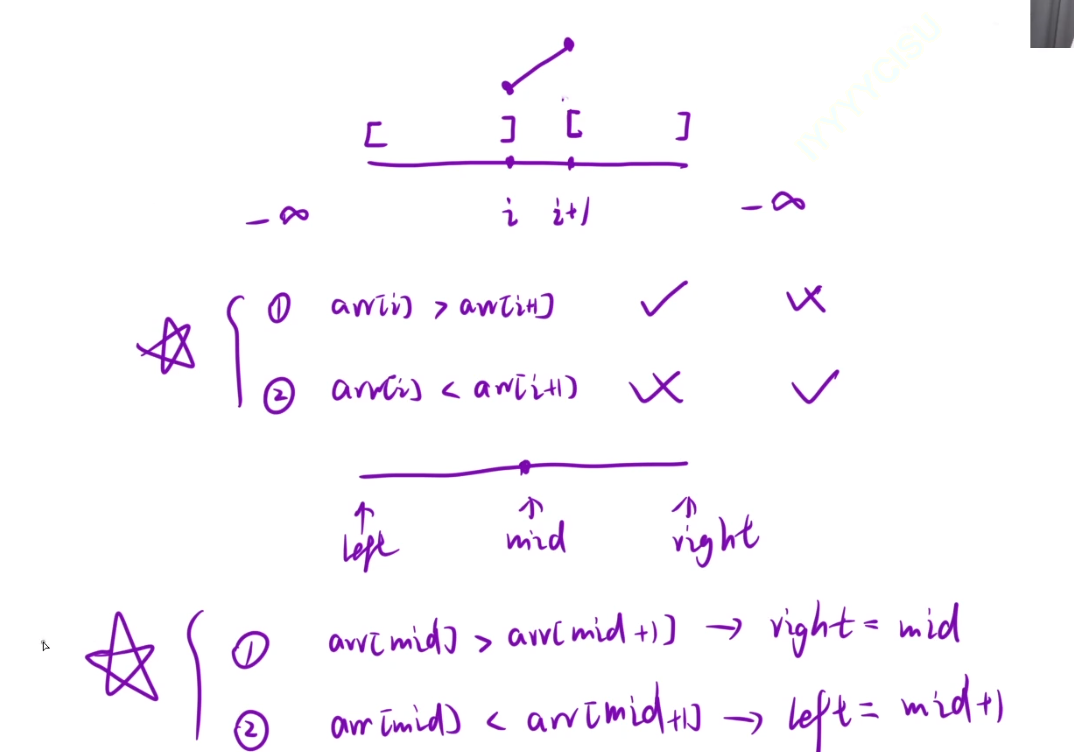
class Solution {
public:int findPeakElement(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]>nums[mid+1]) right=mid;else left=mid+1;} return left;}
};7、寻找旋转排序数组的最小值

算法思路:
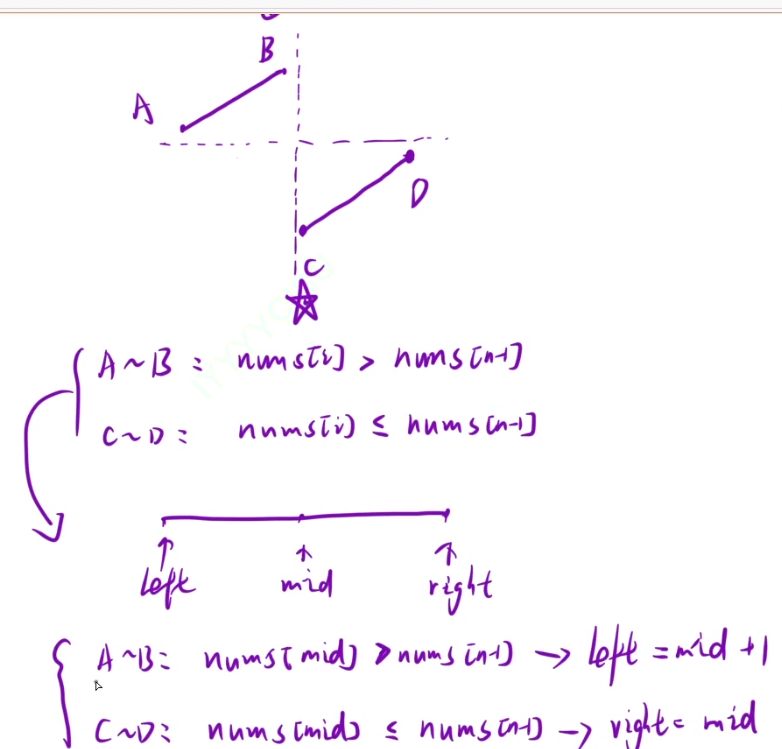
class Solution {
public:int findMin(vector<int>& nums) {int left=0,right=nums.size()-1;int x=nums[right];//最后一点的值while(left<right){int mid=left+(right-left)/2;if(nums[mid]>x) left=mid+1;else right=mid;}return nums[left];}
};8、0~n-1中缺失的数字
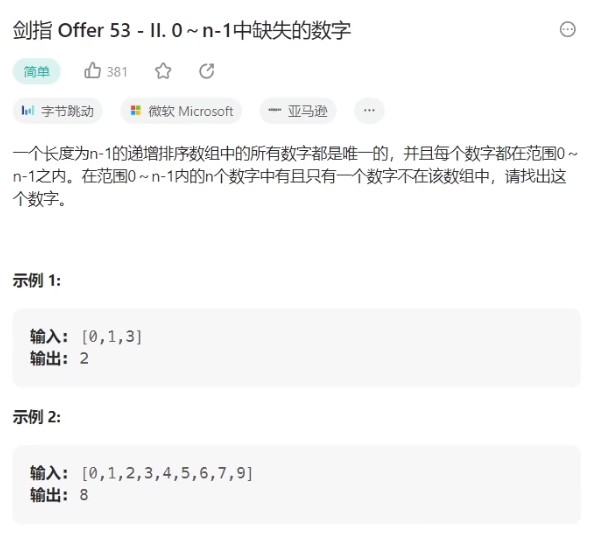
算法原理:
class Solution {
public:int missingNumber(vector<int>& nums){//算法五:二分查找int left=0,right=nums.size()-1;while (left<right){int mid=left+(right-left)/2;if(nums[mid]==mid) left=mid+1;else right=mid;}//处理细节问题return nums[left]==left?left+1:left;}
};本期关于二分查找算法的内容到这里就结束了,喜欢请点个赞,谢谢
