深度学习②【优化算法（重点！）、数据获取与模型训练全解析】

---

先言

在掌握了神经网络的基础架构后，如何让模型高效学习并达到优异性能成为了关键挑战。优化算法的选择、高质量数据集的获取，以及科学的训练技巧，共同决定了深度学习项目的成败。

本文将深入深度学习的实战环节：
✅ 梯度下降优化算法：从SGD到Adam的进化之路
✅ 神经网络数据集获取：公开数据集、自定义数据收集与处理
✅ 模型训练全流程：从数据加载到验证评估的完整Pipeline
✅ 实战技巧：学习率调度、早停机制、模型保存与加载

无论你是希望提升模型效果的研究者，还是准备开展实际项目的工程师，这篇文章都将为你提供系统性的实战指南！

---

一、梯度下降优化算法详解

1.批量梯度下降（BGD）：稳定但计算成本高

Batch Gradient Descent BGD

特点：

• 每次更新参数时，使用整个训练集来计算梯度。

优点：

• 收敛稳定，能准确地沿着损失函数的真实梯度方向下降。
• 适用于小型数据集。

缺点：

• 对于大型数据集，计算量巨大，更新速度慢。

• 需要大量内存来存储整个数据集。

• 公式：
  $$\theta =\theta -\alpha \frac{1}{m}\sum _{i=1}^m{\nabla }_{\theta }L({\hat{y}}^{(i)},y^{(i)})$$
  其中，$m$ 是训练集样本总数，$x^{(i)},y^{(i)}$是第 $i$ 个样本及其标签，${\hat{y}}^{(i)}$是第 $i$ 个样本预测值。

例如，在训练集中有100个样本，迭代50轮。
那么在每一轮迭代中，都会一起使用这100个样本，计算整个训练集的梯度，并对模型更新。
所以总共会更新50次梯度。
因为每次迭代都会使用整个训练集计算梯度，所以这种方法可以得到准确的梯度方向。但如果数据集非常大，那么就导致每次迭代都很慢，计算成本就会很高。
示例代码如下：

#批量梯度下降
#计算量大，需要大量的内存支撑
def test01():#样本x = torch.randn(1000,10)#标签y = torch.randn(1000,1)#神经网络模型model = nn.Linear(10,1)#批量梯度下降dataset = TensorDataset(x,y)dataloader = DataLoader(dataset,batch_size=len(dataset),shuffle=True)criterion = nn.MSELoss()opt = optim.SGD(model.parameters(),lr=0.01)#训练批次epochs = 20for epoch in range(epochs):for x,y in dataloader:#前向传播y_pred = model(x)#计算损失loss = criterion(y_pred,y)#梯度清零opt.zero_grad()#反向传播loss.backward()#更新参数opt.step()print(f'第{epoch+1}次更新损失为：{loss.item()}')print(f'{model.weight.tolist()}, {model.bias.item()}')
# test01()

2.随机梯度下降（SGD）：快速但震荡大

Stochastic Gradient Descent, SGD

特点：

• 每次更新参数时，仅使用一个样本来计算梯度。

优点：

• 更新频率高，计算快，适合大规模数据集。
• 能够跳出局部最小值，有助于找到全局最优解。

缺点：

• 收敛不稳定，容易震荡，因为每个样本的梯度可能都不完全代表整体方向。
• 需要较小的学习率来缓解震荡。

公式：
$$\theta =\theta -\alpha {\nabla }_{\theta }L({\hat{y}}^{(i)},y^{(i)})$$
其中，$x^{(i)},y^{(i)}$ 是当前随机抽取的样本及其标签。

例如，如果训练集有100个样本，迭代50轮，那么每一轮迭代，会遍历这100个样本，每次会计算某一个样本的梯度，然后更新模型参数。

换句话说，100个样本，迭代50轮，那么就会更新100*50=5000次梯度。
因为每次只用一个样本训练，所以迭代速度会非常快。

但更新的方向会不稳定，这也导致随机梯度下降，可能永远都不会收敛。不过也因为这种震荡属性，使得随机梯度下降，可以跳出局部最优解。这在某些情况下，是非常有用的。
示例代码如下：

#随机梯度下降
#收敛快，计算小，但是不稳定，容易震荡
def test03():# 样本x = torch.randn(1000, 10)# 标签y = torch.randn(1000, 1)# 神经网络模型model = nn.Linear(10, 1)# 批量梯度下降dataset = TensorDataset(x, y)dataloader = DataLoader(dataset, batch_size=1, shuffle=True)criterion = nn.MSELoss()opt = optim.SGD(model.parameters(), lr=0.01)# 训练批次epochs = 20for epoch in range(epochs):for x, y in dataloader:# 前向传播y_pred = model(x)# 计算损失loss = criterion(y_pred, y)# 梯度清零opt.zero_grad()# 反向传播loss.backward()# 更新参数opt.step()print(f'第{epoch + 1}次更新损失为：{loss.item()}')print(f'{model.weight.tolist()}, {model.bias.item()}')
#test03()

3.小批量梯度下降（MBGD）：实践中的平衡选择

Mini-batch Gradient Descent MGBD

特点：

• 每次更新参数时，使用一小部分训练集（小批量）来计算梯度。

优点：

• 在计算效率和收敛稳定性之间取得平衡。
• 能够利用向量化加速计算，适合现代硬件（如GPU）。

缺点：

• 选择适当的批量大小比较困难；批量太小则接近SGD，批量太大则接近批量梯度下降。
• 通常会根据硬件算力设置为32\64\128\256等2的次方。

公式：
$$\theta :=\theta -\alpha \frac{1}{b}\sum _{i=1}^b{\nabla }_{\theta }L({\hat{y}}^{(i)},y^{(i)})$$
其中，$b$ 是小批量的样本数量，也就是 $batch\_size$。

例如，如果训练集中有100个样本，迭代50轮。

如果设置小批量的数量是20，那么在每一轮迭代中，会有5次小批量迭代。

换句话说，就是将100个样本分成5个小批量，每个小批量20个数据，每次迭代用一个小批量，因此，按照这样的方式，会对梯度，进行50轮*5个小批量=250次更新。

示例代码如下：

#小批量梯度下降
#计算速度和收敛稳定折中
#批量值选择问题：样本数量过多，计算速度慢，样本数量过少，训练效果不好
def test02():# 样本x = torch.randn(1000, 10)# 标签y = torch.randn(1000, 1)# 神经网络模型model = nn.Linear(10, 1)# 批量梯度下降dataset = TensorDataset(x, y)dataloader = DataLoader(dataset, batch_size=32, shuffle=True)criterion = nn.MSELoss()opt = optim.SGD(model.parameters(), lr=0.01)# 训练批次epochs = 20for epoch in range(epochs):for x, y in dataloader:# 前向传播y_pred = model(x)# 计算损失loss = criterion(y_pred, y)# 梯度清零opt.zero_grad()# 反向传播loss.backward()# 更新参数opt.step()print(f'第{epoch + 1}次更新损失为：{loss.item()}')print(f'{model.weight.tolist()}, {model.bias.item()}')
# test02()

二、梯度下降优化算法：从SGD到Adam

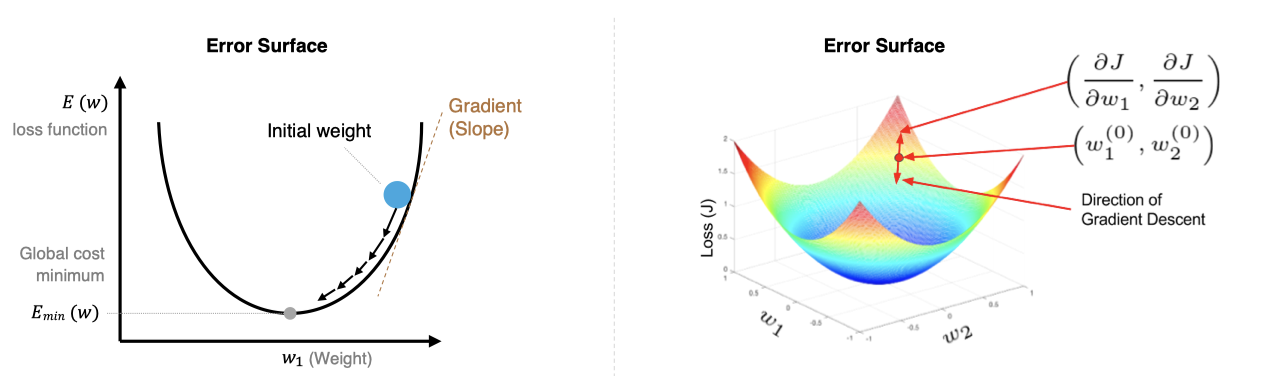
还记的我们在机器学习中知道：梯度下降算法的目标是找到使损失函数 $L(\theta )$ 最小的参数 $\theta$，其核心是沿着损失函数梯度的负方向更新参数，以逐步逼近局部或全局最优解，从而使模型更好地拟合训练数据。同样在深度学习也是一样的任务和目标：

1. 初始化参数：随机初始化模型的参数 $\theta $，如权重 $W$和偏置 $b$。

2. 计算梯度：损失函数 $L(\theta )$对参数 $\theta$ 的梯度 ${\nabla }_{\theta }L(\theta )$，表示损失函数在参数空间的变化率。

3. 更新参数：按照梯度下降公式更新参数：$\theta :=\theta -\alpha {\nabla }_{\theta }L(\theta )$，其中，$\alpha$ 是学习率，用于控制更新步长。

4. 迭代更新：重复【计算梯度和更新参数】步骤，直到某个终止条件（如梯度接近0、不再收敛、完成迭代次数等）。
   

1.指数加权平均

指数加权平均：Exponential Moving Average，简称EMA，是一种平滑时间序列数据的技术，它通过对过去的值赋予不同的权重来计算平均值。与简单移动平均不同，EMA赋予最近的数据更高的权重，较远的数据则权重较低，这样可以更敏感地反映最新的变化趋势。

​ 比如今天股市的走势，和昨天发生的国际事件关系很大，和6个月前发生的事件关系相对肯定小一些。

​ 给定时间序列{xt}\{x_t\}{xt​}，EMA在每个时刻 $t$ 的值可以通过以下递推公式计算：

​ 当$t=1$时：
$$v_0=x_0$$
​ 当$t>1$时：
$$v_t=\beta v_{t-1}+(1-\beta )x_t$$

其中：

• $v_t$ 是第 $t$ 时刻的EMA值；
• $x_t$ 是第 $t$ 时刻的观测值；
• $\beta$ 是平滑系数，取值范围为 $0\le \beta <1$。$\beta$ 越接近 $1$，表示对历史数据依赖性越高；越接近 $0$ 则越依赖当前数据。

公式推导：
$$\begin{gathered} v_t=\beta v_{t-1}+(1-\beta )x_t \\ {v}_{t-1}=\beta v_{t-2}+(1-\beta )x_{t-1} \\ ... \\ 那么： \\ {v}_t=\beta v_{t-1}+(1-\beta )x_t={\beta }^2{v}_{t-2}+\beta (1-\beta )x_{t-1}+(1-\beta )x_t \\ ={\beta }^3{v}_{t-3}+{\beta }^2(1-\beta )x_{t-2}+\beta (1-\beta )x_{t-1}+(1-\beta )x_t \\ ... \\ ={\beta }^t{x}_0+{\beta }^{t-1}(1-\beta )x_1+{\beta }^{t-2}(1-\beta )x_2+...+(1-\beta )x_t \\ ={\beta }^t{x}_0+(1-\beta ){\Sigma }_{i=1}^n{\beta }^{t-i}{x}_i \end{gathered}$$
从上述公式可知：

• 当 β接近 1 时，${\beta }^k$衰减较慢，因此历史数据的权重较高。
• 当 β接近 0 时，${\beta }^k$衰减较快，因此历史数据的权重较低。

2.动量梯度下降（Momentum）

动量（Momentum）是对梯度下降的优化方法，可以更好地应对梯度变化和梯度消失问题，从而提高训练模型的效率和稳定性。它通过引入 指数加权平均 来积累历史梯度信息，从而在更新参数时形成“动量”，帮助优化算法更快地越过局部最优或鞍点。

梯度更新算法包括两个步骤：

a. 更新动量项

首先计算当前的动量项 $v_t$： $v_t=\beta v_{t-1}+(1-\beta ){\nabla }_{\theta }J({\theta }_t)$ 其中：

• $v_{t-1}$ 是之前的动量项；
• $\beta$ 是动量系数（通常为 0.9）；
• ${\nabla }_{\theta }J({\theta }_t)$ 是当前的梯度；

b. 更新参数

利用动量项更新参数：
$$\begin{gathered} v_t=\beta v_{t-1}+(1-\beta ){\nabla }_{\theta }J({\theta }_t) \\ {\theta }_t={\theta }_{t-1}-\eta v_t \end{gathered}$$
特点：

• 惯性效应： 该方法加入前面梯度的累积，这种惯性使得算法沿着当前的方向继续更新。如遇到鞍点，也不会因梯度逼近零而停滞。

• 减少震荡： 该方法平滑了梯度更新，减少在鞍点附近的震荡，帮助优化过程稳定向前推进。

• 加速收敛： 该方法在优化过程中持续沿着某个方向前进，能够更快地穿越鞍点区域，避免在鞍点附近长时间停留。

Momentum 算法是对梯度值的平滑调整，但是并没有对梯度下降中的学习率进行优化。

3.学习率自适应算法（AdaGrad）

AdaGrad（Adaptive Gradient Algorithm）为每个参数引入独立的学习率，它根据历史梯度的平方和来调整这些学习率。具体来说，对于频繁更新的参数，其学习率会逐渐减小；而对于更新频率较低的参数，学习率会相对较大。AdaGrad避免了统一学习率的不足，更多用于处理稀疏数据和梯度变化较大的问题。

AdaGrad流程：

1. 初始化：

   • 初始化参数 ${\theta }_0$ 和学习率 $\eta$。
   • 将梯度累积平方的向量 $G_0$ 初始化为零向量。

2. 梯度计算：

   • 在每个时间步 $t$，计算损失函数$J(\theta )$对参数 $\theta$ 的梯度$g_t={\nabla }_{\theta }J({\theta }_t)$。

3. 累积梯度的平方：

   • 对每个参数 $i$累积梯度的平方：
     $$G_t=G_{t-1}+g_t^2$$
     其中$G_t$ 是累积的梯度平方和，$ g_{t}$ 是第$i$个参数在时间步$t$ 的梯度。

     推导：
     $$G_t=G_{t-1}+g_t^2=G_{t-2}+g_{t-1}^2+g_t^2=...=g_1^2+...+g_{t-1}^2+g_t^2$$

4. 参数更新：

   • 利用累积的梯度平方来更新参数：
     $${\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{G_t+ϵ}}{g}_t$$

   • 其中：

     • $\eta$ 是全局的初始学习率。
     • $ϵ$ 是一个非常小的常数，用于避免除零操作（通常取$10^{-8}$）。
     • $\frac{\eta }{\sqrt{G_t+ϵ}}$ 是自适应调整后的学习率。

AdaGrad 为每个参数分配不同的学习率：

• 对于梯度较大的参数，Gt较大，学习率较小，从而避免更新过快。
• 对于梯度较小的参数，Gt较小，学习率较大，从而加快更新速度。

可以将 AdaGrad 类比为：

• 梯度较大的参数：类似于陡峭的山坡，需要较小的步长（学习率）以避免跨度过大。
• 梯度较小的参数：类似于平缓的山坡，可以采取较大的步长（学习率）以加快收敛。

优点：

• 自适应学习率：由于每个参数的学习率是基于其梯度的累积平方和 $G_{t,i}$ 来动态调整的，这意味着学习率会随着时间步的增加而减少，对梯度较大且变化频繁的方向非常有用，防止了梯度过大导致的震荡。
• 适合稀疏数据：AdaGrad 在处理稀疏数据时表现很好，因为它能够自适应地为那些较少更新的参数保持较大的学习率。

缺点：

1. 学习率过度衰减：随着时间的推移，累积的时间步梯度平方值越来越大，导致学习率逐渐接近零，模型会停止学习。
2. 不适合非稀疏数据：在非稀疏数据的情况下，学习率过快衰减可能导致优化过程早期停滞。

4.加权自适应学习率（AdaGrad ）

虽然 AdaGrad 能够自适应地调整学习率，但随着训练进行，累积梯度平方 $G_t$会不断增大，导致学习率逐渐减小，最终可能变得过小，导致训练停滞。

RMSProp（Root Mean Square Propagation）是一种自适应学习率的优化算法，在时间步中，不是简单地累积所有梯度平方和，而是使用指数加权平均来逐步衰减过时的梯度信息。旨在解决 AdaGrad 学习率单调递减的问题。它通过引入 指数加权平均 来累积历史梯度的平方，从而动态调整学习率。

公式为：
$$\begin{gathered} s_t=\beta \cdot s_{t-1}+(1-\beta )\cdot g_t^2 \\ {\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{s_t+ϵ}}\cdot gt \end{gathered}$$
其中：

• $s_t$是当前时刻的指数加权平均梯度平方。
• β是衰减因子，通常取 0.9。
• η是初始学习率。
• ϵ是一个小常数（通常取 $10^{-8}$），用于防止除零。
• $g_t$是当前时刻的梯度。

优点

• 适应性强：RMSProp自适应调整每个参数的学习率，对于梯度变化较大的情况非常有效，使得优化过程更加平稳。

• 适合非稀疏数据：相比于AdaGrad，RMSProp更加适合处理非稀疏数据，因为它不会让学习率减小到几乎为零。

• 解决过度衰减问题：通过引入指数加权平均，RMSProp避免了AdaGrad中学习率过快衰减的问题，保持了学习率的稳定性

缺点

依赖于超参数的选择：RMSProp的效果对衰减率 $\gamma$ 和学习率 $\eta$ 的选择比较敏感，需要一些调参工作。

5.自适应动量算法（Adaptive Moment Estimation）

Adam（Adaptive Moment Estimation）算法将动量法和RMSProp的优点结合在一起：

• 动量法：通过一阶动量（即梯度的指数加权平均）来加速收敛，尤其是在有噪声或梯度稀疏的情况下。
• RMSProp：通过二阶动量（即梯度平方的指数加权平均）来调整学习率，使得每个参数的学习率适应其梯度的变化。

Adam过程

1. 初始化：

   • 初始化参数 ${\theta }_0$ 和学习率$\eta$。
   • 初始化一阶动量估计 $m_0=0$ 和二阶动量估计$v_0=0$。
   • 设定动量项的衰减率 ${\beta }_1$ 和二阶动量项的衰减率${\beta }_2$，通常 ${\beta }_1=0.9$，${\beta }_2=0.999$。
   • 设定一个小常数$ϵ$（通常取$10^{-8}$），用于防止除零错误。

2. 梯度计算：

   • 在每个时间步 $t$，计算损失函数$J(\theta )$ 对参数$\theta$ 的梯度$g_t = \nabla_\theta J(\theta_t) $。

3. 一阶动量估计（梯度的指数加权平均）：

   • 更新一阶动量估计：
     $$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$$
     其中，$m_t$ 是当前时间步 $t$ 的一阶动量估计，表示梯度的指数加权平均。

4. 二阶动量估计（梯度平方的指数加权平均）：

   • 更新二阶动量估计：
     $$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$$
     其中，$v_t$ 是当前时间步 $t$ 的二阶动量估计，表示梯度平方的指数加权平均。

5. 偏差校正：

   由于一阶动量和二阶动量在初始阶段可能会有偏差，以二阶动量为例：

   在计算指数加权平均时，初始化 $v_0=0$，那么$v_1=0.999\cdot v_0+0.001\cdot g_1^2$，得到$v_1=0.001\cdot g_1^2$，显然得到的 $v_1$ 会小很多，导致估计的不准确，以此类推：

   根据：$v_2=0.999\cdot v_1+0.001\cdot g_2^2$，把 $v_1$ 带入后，
   得到：$v_2=0.999\cdot 0.001\cdot g_1^2+0.001\cdot g_2^2$，导致 $v_2$ 远小于 $g_1$ 和 $g_2$，所以 $v_2$ 并不能很好的估计出前两次训练的梯度。

   所以这个估计是有偏差的。

   使用以下公式进行偏差校正：
   $$\begin{gathered} {\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t} \\ {\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t} \end{gathered}$$
   其中，${\hat{m}}_t$ 和${\hat{v}}_t$ 是校正后的一阶和二阶动量估计。

三、神经网络数据集获取与处理

1.数据加载与数据增强

数据加载：

数据加载器DataLoader 是一个迭代器，用于从 Dataset 中批量加载数据。它的主要功能包括：

• 批量加载：将多个样本组合成一个批次。
• 打乱数据：在每个 epoch 中随机打乱数据顺序。
• 多线程加载：使用多线程加速数据加载。

创建DataLoader并获取：

from torchvision import datasets
import torch.nn as nn
import torch
from torch.utils.data import DataLoader
#获取训练数据集
dataset = datasets.ImageFolder(root="./data", train=True, download=True)
# 创建 DataLoader 
dataloader = DataLoader(dataset,          # 数据集batch_size=10,    # 批量大小shuffle=True,     # 是否打乱数据num_workers=2     # 使用 2 个子进程加载数据
)
# 遍历 DataLoader
# enumerate返回一个枚举对象（iterator），生成由索引和值组成的元组
for batch_idx, (samples, labels) in enumerate(dataloader):print(f"Batch {batch_idx}:")print("Samples:", samples)print("Labels:", labels)

数据增强：

数据增强（Data Augmentation）是一种通过人工生成或修改训练数据来增加数据集多样性的技术，常用于解决过拟合问题。数据增强通过“模拟”更多训练数据，迫使模型学习泛化性更强的规律，而非训练集中的偶然性模式。其本质是一种低成本的正则化手段，尤其在数据稀缺时效果显著。

在了解计算机如何处理图像之前，需要先了解图像的构成元素。

图像是由像素点组成的，每个像素点的值范围为: [0, 255], 像素值越大意味着较亮。比如一张 200x200 的图像, 则是由 40000 个像素点组成, 如果每个像素点都是 0 的话, 意味着这是一张全黑的图像。

我们看到的彩色图一般都是多通道的图像, 所谓多通道可以理解为图像由多个不同的图像层叠加而成, 例如我们看到的彩色图像一般都是由 RGB 三个通道组成的，还有一些图像具有 RGBA 四个通道，最后一个通道为透明通道，该值越小，则图像越透明。

数据增强是提高模型泛化能力（鲁棒性）的一种有效方法，尤其在图像分类、目标检测等任务中。数据增强可以模拟更多的训练样本，从而减少过拟合风险。数据增强通过torchvision.transforms模块来实现。

数据增强的好处

​ 大幅度降低数据采集和标注成本；

​ 模型过拟合风险降低，提高模型泛化能力；

常用变换类

• transforms.Compose：将多个变换操作组合成一个流水线。
• transforms.ToTensor：将 PIL 图像或 NumPy 数组转换为 PyTorch 张量，将图像数据从 uint8 类型 (0-255) 转换为 float32 类型 (0.0-1.0)。
• transforms.Normalize：对张量进行标准化。
• transforms.Resize：调整图像大小。
• transforms.CenterCrop：从图像中心裁剪指定大小的区域。
• transforms.RandomCrop：随机裁剪图像。
• transforms.RandomHorizontalFlip：随机水平翻转图像。
• transforms.RandomVerticalFlip：随机垂直翻转图像。
• transforms.RandomRotation：随机旋转图像。
• transforms.ColorJitter：随机调整图像的亮度、对比度、饱和度和色调。
• transforms.RandomGrayscale：随机将图像转换为灰度图像。
• transforms.RandomResizedCrop：随机裁剪图像并调整大小。

代码示例：

from torchvision import datasets,transforms
import torch.nn as nn
import torch
from torch.utils.data import DataLoader
#创建transforms对象实例
transform = transforms.Compose([
#数据增强的一系列操作transforms.ToTensor(),#随机旋转transforms.RandomRotation(30),#模糊transforms.GaussianBlur(3, sigma=(0.1, 2.0)),#随机翻转transforms.RandomHorizontalFlip(),#缩放transforms.Resize((224, 224)),transforms.RandomResizedCrop(224, scale=(0.8, 1.0)),transforms.ColorJitter(brightness=0.2, contrast=0.2, saturation=0.2),transforms.RandomAffine(degrees=0, translate=(0.1, 0.1)),  # 随机平移transforms.RandomGrayscale(p=0.1),  # 随机灰度化transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])])
#加载相对目录data下的文件
trainset = datasets.ImageFolder(root="./data", train=True, download=True, transform=transform)
dataloader = DataLoader(trainset, batch_size=4, shuffle=False)# 遍历获取每一个批次的数据
for data,target in dataloader:print(data.shape)print(target.shape) 

2.公开数据集资源

2.1获取MNIST数据集

在获取数据集之前先创建一个数据集目录（这里创建名为dataset）用于存放获取的数据集包之后通过datasets的类方法获取相应的数据集，示例代码如下：

import torch
from torch import nn
from torchvision import transforms,datasets
#数据装tensor方法封装
transform = transforms.Compose([transforms.ToTensor()])
#获取训练数据集train_dataset= datasets.MNIST('./datasets',train=True,download=True,transform=transform)
#获取测试数据集eval_dataset = datasets.MNIST('./datasets',train=False,download=True,transform=transform)

2.2获取CIFAR10数据集

同MNIST数据集一样，本地目录没有数据会重新下载在指定目录下，示例如下：

import torch
from torch import nn
from torchvision import transforms,datasets
from PIL import Image
from torch.utils.data import DataLoaderdef build_data():#创建transforms对象transform = transforms.Compose([transforms.ToTensor()])#获取数据集train_dataset= datasets.CIFAR10('./datasets',train=True,download=True,transform=transform)eval_dataset = datasets.CIFAR10('./datasets',train=False,download=True,transform=transform)#dataloader分离特征和标签train_loader = DataLoader(train_dataset,batch_size=128,shuffle=True)eval_loader = DataLoader(eval_dataset,batch_size=len(eval_dataset),shuffle=True)return train_loader,eval_loader

3.自定义数据集资源

3.1手动添加数据数据源

一开始的数据手动进行分类（不同类的图像文件放在名为类别的目录）就存放在data目录下，可以直接用ImageFolder内置方法直接读取

trainset = datasets.ImageFolder(root="./data", train=True, download=True, transform=transform)
dataloader = DataLoader(trainset, batch_size=4, shuffle=False)

3.2通过爬虫爬取网页数据作为数据源

爬虫读取后存放数据的格式要满足如下格式要求：

data/
├── train/
│   ├── beagle/
│   │   ├── img1.jpg
│   │   └── ...
│   ├── chihuahua/
│   │   └── ...
│   └── ...
└── val/├── beagle/│   ├── img5.jpg│   └── ...├── chihuahua/│   └── ...└── ...

这里以百度图片获取猫狗分类数据集为例，代码如下：

import os.path
import requests
import json
#分类
category = {"cat": "猫","dog": "狗"
}
basepath  = os.path.dirname(__file__)
Page_sum=5
if __name__ == '__main__':for k,word in category.items():folder = os.path.join(basepath,k)if not os.path.exists(folder):os.mkdir(folder)for page in range(Page_sum):url = f'https://image.baidu.com/search/acjson?tn=resultjson_com&word={word}&ie=utf-8&fp=result&fr=&ala=0&applid=9065640523184652929&pn={30*page}&rn=30&nojc=0&gsm=12c&newReq=1'headers = {'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/138.0.0.0 Safari/537.36 Edg/138.0.0.0'}response = requests.get(url,headers=headers)images = response.json().get('data').get('images')print(images)imagelist=[]for image in images:imagelist.append(image.get('thumburl','None'))for index,img in enumerate(imagelist):imgdata = requests.get(img).contentwith open(os.path.join(folder,f'{k}_{page*30+index+1}.jpg'),'wb') as f:f.write(imgdata)print(f'关键词：{word} → {k}_{(page * 30 + index)+1}.jpg 保存成功......')

通过上述操作可以得到两个名分别为cat何dog的目录文件，将他们存放在data目录下，通过前一小节方式通过ImageFolder方法读取训练数据集。

四、实战案例：CIFAR-10图像分类

1.获取数据并进行数据增强和划分

代码示例：

def build_data():#创建transforms对象transform = transforms.Compose([transforms.ToTensor()])#获取数据集train_dataset= datasets.CIFAR10('./datasets',train=True,download=True,transform=transform)eval_dataset = datasets.CIFAR10('./datasets',train=False,download=True,transform=transform)#dataloader分离特征和标签train_loader = DataLoader(train_dataset,batch_size=128,shuffle=True)eval_loader = DataLoader(eval_dataset,batch_size=len(eval_dataset),shuffle=True)return train_loader,eval_loader#返回的是训练集和测试集

2.构建网络模型

示例如下：

#构建全连接神经网络结构
class MyNet(nn.Module):def __init__(self,in_features,out_features):super().__init__()self.fc1 = nn.Linear(in_features, 1024)self.bn1 = nn.BatchNorm1d(1024)self.fc2 = nn.Linear(1024, 512)self.bn2 = nn.BatchNorm1d(512)self.fc3 = nn.Linear(512, 256)self.bn3 = nn.BatchNorm1d(256)self.fc4 = nn.Linear(256, 64)self.bn4 = nn.BatchNorm1d(64)self.fc5 = nn.Linear(64, out_features)self.relu = nn.ReLU()self.dropout = nn.Dropout(0.1)def forward(self, x):x = x.view(-1, 32 * 32 * 3)x = self.relu(self.bn1(self.fc1(x)))# x= self.dropout(x)x = self.relu(self.bn2(self.fc2(x)))x = self.relu(self.bn3(self.fc3(x)))x = self.relu(self.bn4(self.fc4(x)))x = self.fc5(x)return x

3.创建训练函数

示例如下：

def train(model,train_loader,lr,epochs):model.train()criterion = nn.CrossEntropyLoss()#添加正则化系数XXopt = torch.optim.SGD(model.parameters(),lr=lr)for epoch in range(epochs):correct = 0#小批量训练for x_train,y_train in train_loader:y_pred = model(x_train)loss = criterion(y_pred,y_train)opt.zero_grad()loss.backward()opt.step()_,index = torch.max(y_pred,dim=1)correct+= (index==y_train).sum().item()correct/=len(train_loader.dataset)print(f'第{epoch+1}次更新损失为：{loss.item()}, 准确率为：{correct}')return loss.item()

4.创建测试函数

示例如下：

def eval(model,eval_loader):model.eval()correct = 0with torch.no_grad():for x_test,y_test in eval_loader:y_pred = model(x_test)_,index = torch.max(y_pred,dim=1)correct += (index==y_test).sum().item()acc = correct/len(eval_loader.dataset)print(f'测试集预测结果准确率为：{acc}')

5.模型的保存和应用

def save():model = MyNet()torch.save(model.state_dict(),'./model/cifar10_model_params.pt')
def load(modelpath):model = MyNet()model.load_state_dict(torch.load(modelpath))return  model

6.应用模型进行图像预测

def predict(model,image_path):model.eval()image = Image.open(image_path)transform = transforms.Compose([transforms.Resize((32,32)),transforms.ToTensor(),])image = transform(image).unsqueeze(0)with torch.no_grad():y_pred = model(image)_,index = torch.max(y_pred,dim=1)class_names = ['airplane','automobile','bird','cat','deer','dog','frog','horse','ship','truck']print(f'预测结果为：{index.item()}，该图中为：{class_names[index.item()]}')

7.完整代码

import torch
from torch import nn
from torchvision import transforms,datasets
from PIL import Image
import matplotlib.pyplot as plt
from torch.utils.data import DataLoaderdef build_data():#创建transforms对象transform = transforms.Compose([transforms.ToTensor()])#获取数据集train_dataset= datasets.CIFAR10('./datasets',train=True,download=True,transform=transform)eval_dataset = datasets.CIFAR10('./datasets',train=False,download=True,transform=transform)#dataloader分离特征和标签train_loader = DataLoader(train_dataset,batch_size=128,shuffle=True)eval_loader = DataLoader(eval_dataset,batch_size=len(eval_dataset),shuffle=True)return train_loader,eval_loader#构建全连接神经网络结构
class MyNet(nn.Module):def __init__(self,in_features,out_features):super().__init__()self.fc1 = nn.Linear(in_features, 1024)self.bn1 = nn.BatchNorm1d(1024)self.fc2 = nn.Linear(1024, 512)self.bn2 = nn.BatchNorm1d(512)self.fc3 = nn.Linear(512, 256)self.bn3 = nn.BatchNorm1d(256)self.fc4 = nn.Linear(256, 64)self.bn4 = nn.BatchNorm1d(64)self.fc5 = nn.Linear(64, out_features)self.relu = nn.ReLU()self.dropout = nn.Dropout(0.1)def forward(self, x):x = x.view(-1, 32 * 32 * 3)x = self.relu(self.bn1(self.fc1(x)))# x= self.dropout(x)x = self.relu(self.bn2(self.fc2(x)))x = self.relu(self.bn3(self.fc3(x)))x = self.relu(self.bn4(self.fc4(x)))x = self.fc5(x)return xdef train(model,train_loader,lr,epochs):model.train()criterion = nn.CrossEntropyLoss()#添加正则化系数XXopt = torch.optim.SGD(model.parameters(),lr=lr)for epoch in range(epochs):correct = 0#小批量训练for x_train,y_train in train_loader:y_pred = model(x_train)loss = criterion(y_pred,y_train)opt.zero_grad()loss.backward()opt.step()_,index = torch.max(y_pred,dim=1)correct+= (index==y_train).sum().item()correct/=len(train_loader.dataset)print(f'第{epoch+1}次更新损失为：{loss.item()}, 准确率为：{correct}')return loss.item()
def eval(model,eval_loader):model.eval()correct = 0with torch.no_grad():for x_test,y_test in eval_loader:y_pred = model(x_test)_,index = torch.max(y_pred,dim=1)correct += (index==y_test).sum().item()acc = correct/len(eval_loader.dataset)print(f'测试集预测结果准确率为：{acc}')
def save():model = MyNet()torch.save(model.state_dict(),'./model/cifar10_model_params.pt')
def load(modelpath):model = MyNet()model.load_state_dict(torch.load(modelpath))return  modeldef predict(model,image_path):model.eval()image = Image.open(image_path)transform = transforms.Compose([transforms.Resize((32,32)),transforms.ToTensor(),])image = transform(image).unsqueeze(0)with torch.no_grad():y_pred = model(image)_,index = torch.max(y_pred,dim=1)class_names = ['airplane','automobile','bird','cat','deer','dog','frog','horse','ship','truck']print(f'预测结果为：{index.item()}，该图中为：{class_names[index.item()]}')
if __name__ == '__main__':train_loader,eval_loader = build_data()model = MyNet() #模型初始化# train(model,train_loader,0.01,20)# save()#这里的模型已经进过训练直接通过参数字典拿来用，不过需要进过初始化model = load('./model/cifar10_model_params.pt')eval(model, eval_loader)image_path = './image/100.jpg'predict(model,image_path)

通过训练得知图像对于三通道的有色图像进行预测的准确度比较低，捅咕部分优化手段任然处在不理想的结果，这是正常现象
单纯的全连接网络模型对于图像的预测能力是有缺陷的，在网络结构中对图像数据进行前向传播时，图像的像素特征被映射为一个一维向量，因此图像的空间特征结构收到损坏，模型无法的到真实的图像特征或是特征不完全，所以在下一章节我们将用到卷积核的方式对图像进行特征提取，也就是卷积神经网络，它对我们的图像进行分类有意想不到的效果。

---

结语

掌握优化算法的原理、熟练获取和处理数据、构建高效的训练流程，是成为深度学习实践者的必备技能。本文从理论到代码实战，为你提供了完整的深度学习项目指南。

🔧 动手实践：文中包含可运行的代码示例，建议在Colab或本地环境中亲自尝试！你在模型训练中遇到过哪些挑战？欢迎在评论区分享交流！

📌 下篇预告：《卷积神经网络实战：从LeNet到EfficientNet的图像分类全解析》